Численные методы решения уравнений в среде MATHCAD

 

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ В СРЕДЕ MATHCAD

 

Введение. 3

Глава 1. ОСНОВЫ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ.. 4

1.1. История возникновения школьной информатики и компьютерного моделирования в школе. 4

1.2. Требования ФГОС к преподаванию информатики и компьютерного моделирования в школе. 8

1.3. Анализ школьных учебников по информатике, содержащих тему компьютерное моделирование. 10

1.4. Основные сведения по курсу компьютерного моделирования. 12

1.5. Компьютерные среды и языки программирования, используемые для создания модели. 14

1.6. Опыт школьных учителей информатики в преподавании компьютерного моделирования. 20

Глава 2. СОЗДАНИЕ КОМПЬЮТЕРНОЙ МОДЕЛИ В MATHCAD.. 22

2.1. Постановка задачи. 22

2.2. Построение математической модели. 22

2.3. Построение компьютерной модели. 24

2.4. Эксплуатация и тестирование модели. 28

2.5. Выводы и рекомендации по данной модели. 30

2.6. Методические рекомендации для школьных учителей информатики. 30

Заключение. 32

Список литературы. 33

 

Введение

Курс «Компьютерное моделирование» интегрирует в себе многие дисциплины: математика, численные методы, физика, экономика, программирование. Значимость этого раздела велика, так как учащиеся начинают воспринимать компьютер не только как средство обучения, но и как инструмент при решении задач из различных областей науки и техники. Поэтому будет актуальным рассмотреть численные методы решения уравнений в рамках компьютерного моделирования в среде Mathcad. Эта система наиболее удобна для быстрых вычислений во многих областях знаний. Простота программирования, возможность численных и аналитических вычислений делают Mathcad удобной средой моделирования даже для пользователей, далеких от тонкостей программирования.

Целью данного исследования является создание компьютерной модели решения уравнений численными методами в среде Mathcad. Для достижения поставленной цели будут решены следующие задачи:

1.                 Анализ научной, методической литературы по теме «Компьютерное моделирование».

2.                 Анализ документации на предмет изучения компьютерного моделирования в школе.

3.                 Создание компьютерной модели в среде Mathcad.

Объектом исследования является решение уравнений посредствам компьютерного моделирования. Предмет исследования – возможности построения решений уравнений методом половинного деления в среде Mathcad.

Данная работа способствует наглядному представлению междисциплинарных связей математики и информатики и основной задачи ЭВМ – автоматизации труда и повышение эффективности научных исследований.

 

Глава 1. ОСНОВЫ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ

1.1. История возникновения школьной информатики и компьютерного моделирования в школе

Компьютерное моделирование можно назвать одним из самых сложных разделов школьного курса информатики. Только в программе курса он появился не сразу. Рассмотрим историю становления школьного курса информатики.

Первые опыты преподавания информатики в советской школе начались за тридцать лет до реформы образования, которая ввела данный предмет в массы. В 1959 году в нескольких школах Москвы и Новосибирска старшеклассников обучали программированию, теории информации и материальной части компьютеров тех времен. Это объяснялось тем, что первый опыт эксплуатации советских электронно-вычислительных машин выявил острую необходимость в квалифицированной обслуживающем персонале, который должен был понимать принципы работы ЭВМ и уметь с ней взаимодействовать. Так и получилось, в двух городах, в которых был самый большой парк вычислительной техники, были разработаны школьные учебные планы для решения текущих задач: в Новосибирске под руководством Андрея Петровича Ершова, в Москве – Семена Исааковича Шварцбурда.

С 1 сентября 1985 года курс «Основы информатики и вычислительной техники» был введен во все советские образовательные школы в качестве обязательного предмета. В помощь учителям в этом же году А.П. Ершов и В.М. Монахова выпускают пробное учебное пособие в двух частях для средних учебных заведений «Основы информатики и вычислительной техники» [6]. Данное пособие содержало первоначальные сведения об электронно-вычислительных машинах, их устройстве и применении, о подготовке решения задач на ЭВМ с помощью алгоритмов. В конце каждого параграфа приводились вопросы для повторения теории и упражнения для закрепления материала [5].

Данный курс информатики, который ввели в школы в 1985 году, в течение 10 лет оставался практически неизменным. В конце 1980-х – начале 1990-х годов появились школьные учебники других авторов, но цели обучения информатики значительно отличались. Учебник В.А. Каймина (2 статьи) ставил целью обучения информатике решение триединой задачи: формирование компьютерной грамотности, логического мышления и информационной культуры школьников. Стоит уточнить, что под компьютерной грамотностью понималось «умение читать, писать, считать, рисовать, а также искать информацию, используя для этого ЭВМ». Учебник же, написанный авторским коллективом: Л.Г. Кушниренко, Г.В. Лебедева, Р.Л. Свореня основной целью обучения информатике называл развитие операционного, т.е. алгоритмического мышления учащихся. Соответственно, в этом учебнике алгоритмы являлись главным понятием, а их составление и анализ – основным видом учебной деятельности школьников.

Также стоит отметить учебник, написанный большим коллективом авторов под руководством А.Г. Гейна в 1993. Данный учебник по ОИВТ имел прикладную направленность, формировал представление о технологии решения практической задачи на ЭВМ таким образом: постановка задачи; построение математической модели; построение алгоритма; составление программы для ЭВМ; получение результата решения задачи с помощью проведения численного эксперимента. Нетрудно заметить, этот учебник уже знакомил учащихся с математическими моделями. И, таким образом, с начала 90-х годов содержание курса школьной информатики начало меняться: стали рассматриваться вопросы моделирования, построения и изучения информационных моделей. Также, постепенно становятся неотъемлемым компонентом всех курсов информатики темы моделирования и формализации. Что отразится на научных работах по информатике тех времен [6].

В конце XX, начале XXI века многие работы С.А. Бешенкова, М.Г. Бояршинова, А.Г. Гейна, И.Г. Захаровой, А.А. Кузнецова, Е.К. Хеннера, А.П. Шестакова и др. были посвящены изучению различных аспектов информационного моделирования. Это объясняется, с одной стороны, значением информационного моделирования в школьном обучении в целом. С другой стороны, тем, что в содержании курса информатики происходил процесс «восстановление позиций» кибернетики, который долго игнорировался в советской науке.

В курсе школьной информатики информационное моделирование рассматривалось и рассматривается в трех аспектах:

1.     как инструмент познания, так как происходит получение знаний о реальном объекте в процессе построения и исследования информационной модели, также приобретаются знания о языках моделирования, которые используются для описания модели;

2.     как средство обучения, так как в процессе обучения используются информационные модели изучаемого объекта: словесное описание, формулы, графическое изображение;

3.     как объект изучения, так как любую информационную модель можно рассматривать как самостоятельных объект с присущими ему свойствами, связями и характеристиками.

Начиная с 1990 гг. в стране стала распространяться зарубежная компьютерная техника. Вследствие чего возникла проблема смещения акцента в преподавании информатики с обучения программированию на прикладной и технологический аспекты. Постепенно стали приходить к мысли, что компьютерная грамотность и умение программировать не совсем одно и то же. Произошла постепенная подмена общеобразовательного содержания курса информатики его прикладным аспектом. Важным событием для всей отечественной системы образования стал закон РФ «Об образовании», который был принят в 1992 г. В соответствии с концепцией образовательных стандартов, провозглашенной в этом законе, был запущен процесс разработки стандартов по всем образовательным областям.

Период с конца 90-х гг. по 2004 г. характеризуется интенсивным осмыслением накопленного опыта. Были сформулированы основные концепции решения назревшей проблемы, опубликованы рекомендации ЮНЕСКО по информатике в начальном образовании, концепции обучения информатике в 12-летней школе. В 2001 г. Утверждена новая трехуровневая структура изучения курса информатики. Изучение информатики рекомендовано начинать со 2 класса. 2002 г. принят Региональный стандарт содержания образования по информатике для средней образовательной школы.

Основная проблема методики преподавания школьной информатики в течение последнего десятилетия – несогласованность содержания и нормативных сроков изучения информатики не только по стране, но и у разных учителей одной школы. В этой связи утверждение федерального компонента стандарта по информатике и ИКТ (05.03.2004 г.) и нового Базисного учебного плана (09.03.2004 г.), начинается новый этап в преподавании информатики в школе. Он характеризуется тем, что предмет получает новое название – «Информатика и информационно-коммуникационные технологии» или сокращенно «Информатика и ИКТ»; определены сроки его изучения: 3–4, 8–9 и 10–11 классы.

1.2. Требования ФГОС к преподаванию информатики и компьютерного моделирования в школе

В настоящее время ФГОС среднего общего образования диктует следующие требования к предметным результатам освоения базового курса информатики касательно компьютерного моделирования: сформированность представлений о компьютерно-математических моделях и необходимости анализа соответствия модели и моделируемого объекта (процесса); о способах хранения и простейшей обработке данных; понятия о базах данных и средствах доступа к ним, умений работать с ними [17].

На углубленном уровне требования к предметным результатам должны дополнительно отражать владение опытом построения и использования компьютерно-математических моделей, проведения экспериментов и статистической обработки данных с помощью компьютера, интерпретации результатов, получаемых в ходе моделирования реальных процессов; умение оценивать числовые параметры моделируемых объектов и процессов, пользоваться базами данных и справочными системами [18]

Согласно примерной основной образовательной программе основного общего образования содержательная линия математического моделирования содержит следующие аспекты [11, 12].

Понятие математической модели. Задачи, решаемые с помощью математического (компьютерного) моделирования. Отличие математической модели от натурной модели и от словесного (литературного) описания объекта. Использование компьютеров при работе с математическими моделями. Компьютерные эксперименты. Примеры использования математических (компьютерных) моделей при решении научно-технических задач. Представление о цикле моделирования: построение математической модели, ее программная реализация, проверка на простых примерах (тестирование), проведение компьютерного эксперимента, анализ его результатов, уточнение модели.

Примерная программа учебного предмета «Информатика» на уровне среднего общего образования описывает следующее содержание по теме «Математическое моделирование» на базовом уровне:

Представление результатов моделирования в виде, удобном для восприятия человеком. Графическое представление данных (схемы, таблицы, графики). Практическая работа с компьютерной моделью по выбранной теме. Анализ достоверности (правдоподобия) результатов экспериментов. Использование сред имитационного моделирования (виртуальных лабораторий) для проведения компьютерного эксперимента в учебной деятельности.

И на углубленном уровне изучение математического моделирования строится следующим образом.

Практическая работа с компьютерной моделью по выбранной теме. Проведение вычислительного эксперимента. Анализ достоверности (правдоподобия) результатов компьютерного эксперимента. Представление результатов моделирования в виде, удобном для восприятия человеком. Графическое представление данных (схемы, таблицы, графики). Построение математических моделей для решения практических задач. Имитационное моделирование. Моделирование систем массового обслуживания. Использование дискретизации и численных методов в математическом моделировании непрерывных процессов. Использование сред имитационного моделирования (виртуальных лабораторий) для проведения компьютерного эксперимента в учебной деятельности. Компьютерный (виртуальный) и материальный прототипы изделия. Использование учебных систем автоматизированного проектирования.

 

 

1.3. Анализ школьных учебников по информатике, содержащих тему компьютерное моделирование

Представим анализ школьных учебников по информатике, содержащих тему «Компьютерное моделирование» в виде таблицы (см. таблицу 1.1) [2-4, 9, 10, 14-16, 19].

Таблица 1.1

класс	автор/авторский коллектив	содержание
8	Семакин И.Г., Залогова Л.А., Русаков С.В., Шестакова Л.В.	Глава II. Информационное моделирование. Что такое моделирование. Графические информационные модели. Табличные модели. Информационное моделирование на компьютере
11	Семакин И.Г., Хеннер Е.К., Шеина Т.Ю.	Глава 3. Информационное моделирование. Компьютерное информационное моделирование. Моделирование зависимостей между величинами. Модели статистического прогнозирования. Моделирование корреляционных зависимостей. Модели оптимального планирования
11	Семакин И.Г., Шеина Т.Ю., Шестакова Л.В. Углубленный уровень	Глава 3. Компьютерное моделирование. Методика математического моделирования на компьютере. Моделирование движения в поле силы тяжести. Моделирование распределения. Компьютерное моделирование в экономике и экологии. Имитационное моделирование
9	Босова Л.Л., Босова А.Ю.	Глава 1. МОДЕЛИРОВАНИЕ И ФОРМАЛИЗАЦИЯ. Моделирование как метод познания. Знаковые модели.
11	Босова Л.Л., Босова А.Ю.	Глава 3. ИНФОРМАЦИОННОЕ МОДЕЛИРОВАНИЕ. Модели и моделирование. Моделирование на графах. База данных как модель предметной области. Системы управления базами данных
9	Поляков К.Ю., Еремин Е.А.	Глава 3. Моделирование. Модели и моделирование. Математическое моделирование.
11	Поляков К.Ю., Еремин Е.А. Углубленный уровень	Глава 2. Моделирование. Модели и моделирование. Системный подход в моделировании. Этапы моделирования. Моделирование движения. Математические модели в биологии. Системы массового обслуживания
10	Гейн А.Г.	Глава III. Моделирование процессов живой и неживой природы. Моделирование физических, биологических и социальных процессов. Границы адекватности модели. Вероятностные модели. Датчики случайных чисел и псевдослучайные последовательности. Моделирование случайных процессов. Метод Монте-Карло. Измерение количества информации (формула Шеннона).

 

1.4. Основные сведения по курсу компьютерного моделирования

Моделью объекта в курсе компьютерного моделирования называют абстрактный образ объекта или явления и отношений между отдельными частями объекта или явления. Любая модель это некоторая абстракция, звено в цепочке познания от опыта к абстракции, к осмыслению. Когда осмыслили снова опыту, к практике. Моделированием называется процесс создания модели.

Модели классифицируются по области использования: учебные, научно-технические, игровые; по отрасли знаний: экономические, исторические, биологические; по способу представления: материальные и абстрактные модели; по учету моделью временного фактора: статические и динамические.

Также все многообразие моделей можно разделить на два класса: натурные модели и информационные. Натурной моделью называется модель материальная, выполненная из физических материалов, ее можно «потрогать руками». Информационные модели делятся на образно-знаковые и знаковые модели.

Образно-знаковые модели учитывают цвет и форму. Их также можно разделить на:

1.     геометрические, отражающие внешний вид оригинала (чертеж, карта, план);

2.     структурные, отражающие строение объектов и связи их параметров (таблица, схема, граф);

3.     словесные, зафиксированные средствами языка;

4.     алгоритмические модели (блок-схема, нумерованный список).

Знаковые модели можно разделить на:

1.     математические модели, представленные математическими формулами, отображающие связи различных параметров объекта, системы, процесса;

2.     специальные модели, представленные на специальных языках (химические формулы, ноты и др.);

3.     алгоритмические модели представлены в виде программы, записанной на специальном языке программирования.

Моделирование с помощью компьютера называется компьютерным моделированием. Основное внимание в разделе «Компьютерное моделирование» уделяется математическим и имитационным моделям. Эти виды моделей широко используются в научных и прикладных исследованиях [16].

Имитационное моделирование – это процесс конструирования на ЭВМ сложной реальной системы функционирующей во времени и подстановки экспериментов на этой модели с целью либо понять поведение системы, либо оценить различные стратегии обеспечив функционирование данной системы.

Любой модели присущи основные свойства:

1.     конечность;

2.     упрощенность;

3.     приблизительность;

4.     адекватность;

5.     наглядность;

6.     целенаправленность;

7.     информативность;

8.     полнота;

9.     замкнутость.

Компьютерное моделирование зачастую связано с построением математической модели. Основываясь на этом, представим основные этапы компьютерного моделирования:

1.     постановка задачи;

2.     построение математической модели;

3.     построение компьютерной модели;

4.     эксплуатация и тестирование модели;

5.     выводы.

1.5. Компьютерные среды и языки программирования, используемые для создания модели

Компьютерная реализация моделирования сопровождается разработкой алгоритма, составлением программы для компьютера или работой в прикладной программе. Существует пакет прикладных программ, т.е. программы, которые рассчитаны на применение в определенной предметной области и дополненные соответствующей технической документацией [7].

Для графической обработки результатов моделирования используются специальные графические средства – пакеты научной и инженерной графики, которые могут реализовать, в том числе, и анимацию, и трехмерное моделирование:

1.     Sweet Home 3D (см. рис. 1.1).

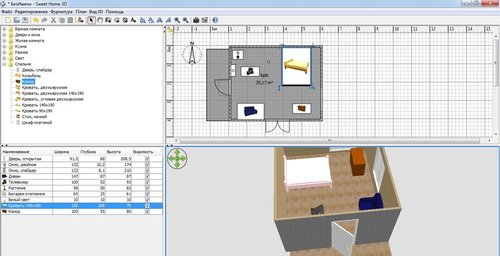
Рис. 1.1.

Программа для моделирования интерьера, архитектурной визуализации жилых пространств и плана дома. Sweet Home 3d полностью русифицирована, так же она имеет большой набор встроенных в программ объектов, стилей и текстур окраски объектов. Встроенные объекты позволяют вам не пытаться рисовать самим, или искать в интернете, например диван, а взять из предложенных вариантов.

2.      SketchUp Make (см. рис. 1.2).

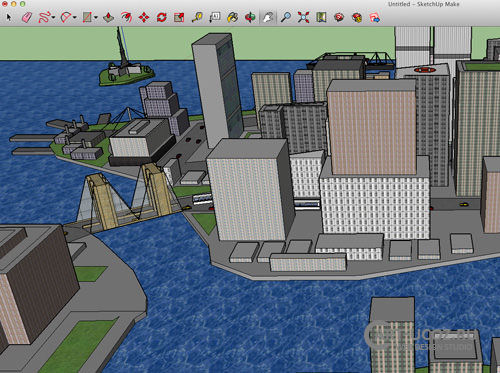
Рис. 1.2

SketchUp Make, одно из самых популярных программ для 3D-моделирования, используется в основном для архитектурных целей, а иногда и для других ниш на рынке 3D-дизайна.

3.     Autodesk 3ds Max (см. рис. 1.3).

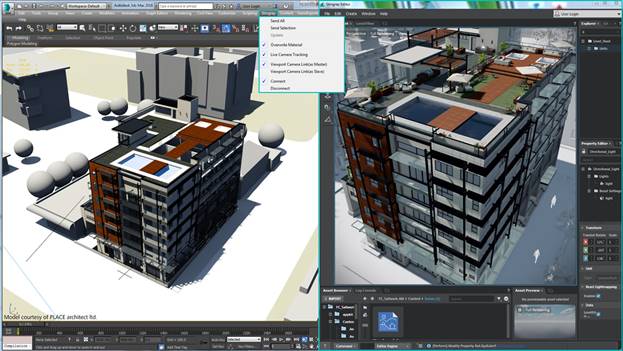
Рис. 1.3

3ds Max — одна из старейших и самых распространенных программ для 3D-моделирования. Для нее выпущено больше всего видеоуроков, курсов и дополнительных расширений.

4.     Cinema 4D (см. рис. 1.4).

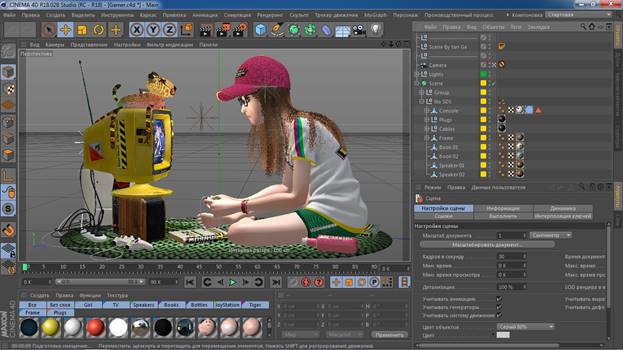
Рис. 1.4

Эту программу отличает приятный и удобный интерфейс, который легче воспринимается новичками. Раньше Cinema 4D использовалась преимущественно для моушн-дизайна, но в последнее время все чаще можно увидеть специалистов из кино и рекламы, работающих в ней. Из минусов можно отметить только стоимость программы и отсутствие студенческой версии.

Для компьютерной реализации не очень сложных математических моделей подходят универсальные прикладные средства выполнения вычислений, универсальные математические пакеты:

1.     MathCad (см. рис. 1.5).

Современное приложение, которое позволит описывать решение задач математики и их алгоритмы в режиме любой сложности. Программа может обработать широчайший объём, как теоретических, так и практических задач.

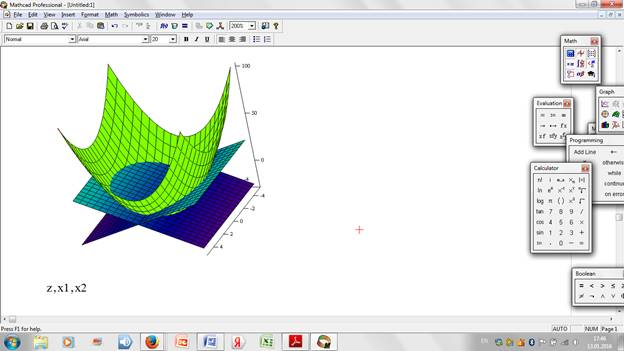
Рис. 1.5

2.     Maple (см. рис. 1.6).

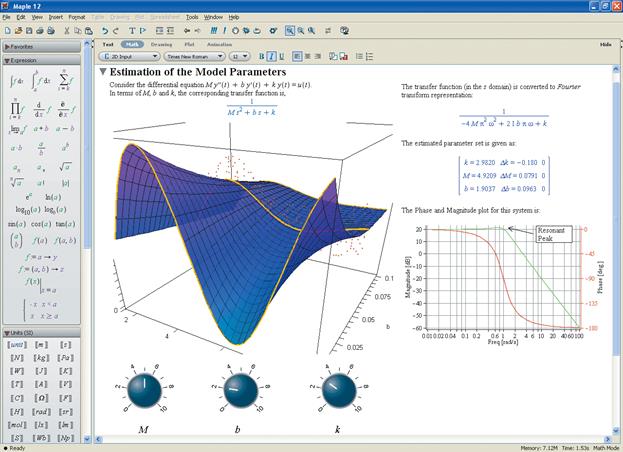
Рис. 1.6

Maple — система компьютерной математики, рассчитанная на широкий круг пользователей. Способна выполнять быстро и эффективно не только символьные, но и численные расчеты, причем сочетает это с превосходными средствами графической визуализации и подготовки электронных документов.

И самым универсальным и гибким способом реализации на компьютере математического моделирования является программирование на универсальных языках. Такой подход позволяет исследователю вносить любые изменения в математическую модель, численный метод ее реализации, управлять точностью получаемых результатов, оптимизировать время вычислений.

1.     Visual Basic (см. рис. 1.7)

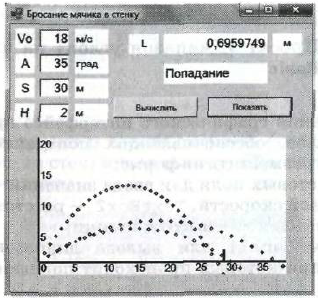
Рис.1.7

Visual Basic представляет собой интегрированную среду разработки, которая содержит набор инструментов, облегчающих и ускоряющих процесс разработки приложений. Причем процесс разработки заключается не в написании программы (программного кода), а в проектировании приложения. Приложение формируется средствами графического редактирования (компоновки), что позволяет свести процесс создания программного кода к минимуму.

2.     Turbo Delphi (см. рис. 1.8).

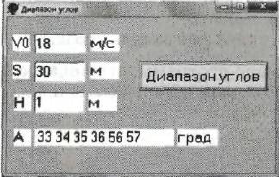
Рис. 1.8

Интегрированная среда программирования предназначена для создания 32х разрядных приложений WINDOWS, относится к классу визуальных, в которых разработчику предоставляется возможность прямо на экране формировать интерфейс разрабатываемого программного продукта из стандартных элементов управления.

 

1.6. Опыт школьных учителей информатики в преподавании компьютерного моделирования

Компьютерное моделирование является одним из самых сложных разделов в школьном курсе информатики. В результате изучения компьютерного моделирования ученики должны понять, что моделирование во всякой области знаний имеет схожие черты. Более того, в большинстве случаев для различных явлений или процессов удается построить очень близкие модели. Также школьники должны усвоить, что и модели, и компьютеры предоставляют возможность познавать окружающий мир и управлять им в интересах человека. Непосредственным условием успешного понимания темы у учащихся является понимание всех преимуществ компьютерного эксперимента по сравнению с другими [1].

Рассмотрим опыт школьных учителей в преподавании компьютерного моделирования на примере учителя информатики из города Мурманска [13]. На сайте подробно представлено планирование уроков по теме «Моделирование и формализация»:

1.        Введение понятий "модель", "моделирование". Подходы к классификации моделей

2.     Этапы моделирования

3.     Формализация. Представление моделей в различной форме

4.     Оценка моделей. Модели мировоззрения

5.        Моделирование в естественных науках. Классические модели физики

6.     Модели в экологии и биологии

7.     Случайные процессы. Моделирование случайных процессов

8.        Моделирование в социальных науках. Простейшие модели социологии

9.     Моделирование в социальных науках. Простейшие модели в экономике

10. Имитационное компьютерное моделирование

11. Зачетный проект «Разные модели одной задачи»

В данном курсе обучения моделирования в качестве инструмента моделирования используются электронные таблицы Excel. Примечательно, что в конце усвоения темы предусматривается защита проектов. Это повышает мотивацию учащихся при решении задач, способствует развитию творческих способностей, формированию чувства ответственности.

Также в дополнительных материалах представлен конспект интегрированного урока по информатике, математике и физике. Учащиеся получают задачу по физике, в математической части производят необходимые расчеты. На этапе, имеющем отношение к информатике, составляют алгоритм действий и заполняют электронную таблицу. И на финальном шаге, анализируют полученные результаты, учитывая законы физики, и находят верный ответ к поставленной задачи. Такой подход вызывает положительные эмоции от новых форм работы, активизирует познавательную деятельность учащихся и позволяет им проследить преемственность школьных дисциплин в реальной жизни [8].

 

Глава 2. СОЗДАНИЕ КОМПЬЮТЕРНОЙ МОДЕЛИ В MATHCAD

2.1. Постановка задачи

Найти корень уравнения

.

 

2.2. Построение математической модели

Решение будем производить численными методами. Для начала следует локализовать корень: определить на каком отрезке он находится. Используем графический метод. Так как функция нестандартная, график функции построить не так просто в явном виде. Поэтому представим нашу функцию как сумму функций  и . И представим их графики на одной координатной плоскости (см. рис. 2.1).

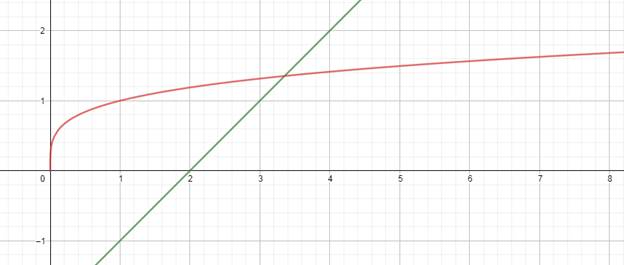
Рис. 2.1

Тогда точка пересечения этих графиков и будет являться корнем нашего уравнения. Получили, что наш корень расположен на отрезке [3;4]. Найдем решение уравнения тремя способами: метод половинного деления, метод секущих, метод касательных.

Метод половинного деления состоит в следующем: мы приближаемся к корню уравнения, последовательно уменьшая длину отрезка. На первом этапе рассматривается середина c найденного отрезка [a;b] и проверяется условие . Т.е. меняется ли знак функции на этом отрезке. Если не меняется, на этом отрезке нет корня, поэтому левый конец отрезка заменяем найденной серединой. Если меняется, значит для дальнейшего приближения заменяем правый конец.

Для нашей задачи

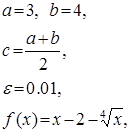
где  – это заданная точность наших вычислений. Стоит также отметить, что условием перехода к следующему шагу отделения отрезка будет являться выполнение условия , поскольку корень всегда заключен внутри отрезка, и итерационный процесс можно останавливать, если длина отрезка станет меньше заданной точности.

В отличие от метода половинного деления, метод секущих предлагает, что деление рассматриваемого интервала будет выполняться не в его середине, а в точке пересечения хорды с осью абсцисс. Следует отметить, что под хордой понимается отрезок, который проведен через точки рассматриваемой функции по концам рассматриваемого интервала. Рассматриваемый метод обеспечивает более быстрое нахождение корня, чем метод половинного деления, при условии задания одинакового рассматриваемого интервала.

Уравнение прямой (хорды), которая проходит через точки А и В имеет следующий вид: .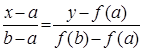

Для точки пресечения прямой с осью абсцисс записанное выше уравнение перепишется в следующем виде: .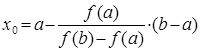

В качестве нового интервала для прохождения итерационного процесса выбираем один из двух или , на концах которого функция принимает значения разных знаков. Противоположность знаков значений функции на концах отрезка можно определить множеством способов. Один из множества этих способов — умножение значений функции на концах отрезка и определение знака произведения путём сравнения результата умножения с нулём:  или . Итерационный процесс уточнения корня заканчивается, когда условие близости двух последовательных приближений станет меньше заданной точности.

Поиск корня функции f(x) методом касательных (также известным как метод Ньютона) сводится к задаче поиска точки пересечения с осью абсцисс касательной, построенной к графику функции f(x).

Проведенная в любой точке касательная линия к графику функции определяется производной данной функции в рассматриваемой точке, которая в свою очередь определяется тангенсом угла α (). Точка пересечения касательной с осью абсцисс определяется исходя из соотношения в прямоугольном треугольнике: тангенс угла определяется отношением противолежащего катета к прилежащему катету. Таким образом, на каждом шаге строится касательная к графику функции в точке очередного приближения  . Точка пересечения касательной с осью Ox будет являться следующей точкой приближения . В соответствии с рассматриваемым методом расчет приближенного значения корня на i-итерации производится по формуле:

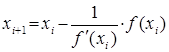
Условием окончания итерационного процесса является выполнение следующего условия: , где  ˗ допустимая погрешность определения корня.

 

2.3. Построение компьютерной модели

Построим компьютерную модель в приложении MathCAD. Для начала представим общие сведения, необходимые для работы с данной программой.

Основное окно приложения имеет ту же структуру, что и большинство

приложений Windows. Сверху вниз располагаются заголовок окна, строка

меню, панели инструментов (стандартная и форматирования) и рабочий лист,

или рабочая область, документа. Новый документ создается автоматически при запуске MathCAD. Файлы документов в MathCAD имеют расширение .mcd (см. рис. 2.2).

Рис. 2.2

Панель инструментов Math (Математика) предназначена для вызова на экран еще девяти панелей, с помощью которых происходит вставка математических операций в документы. Чтобы вызвать какую-либо из них, нужно нажать соответствующую кнопку на панели.

Переменные должны быть предварительно определены пользователем, т. е. им необходимо хотя бы однажды присвоить значение. В качестве оператора присваивания используется знак :=, тогда как знак = отведен для вывода значения константы или переменной. Попытка использовать неопределенную переменную ведет к выводу сообщения об ошибке.

MathCAD читает рабочий документ слева направо и сверху вниз, поэтому определив переменную, ее можно использовать в вычислениях везде правее и ниже равенства, в котором она определена.

Для построения графика используется команда меню Вставка → Графики.

Для составления программ необходимо вызвать панель программирования (на кнопке изображены блок-схемы). Появится панель программирования, состоящая из кнопок:

Кнопка Add Line. При ее нажатии возникает вертикальная линия, объединяющая два оператора в блок с одним входом и одним выходом (см. рис 2.3). Для объединения большего числа операторов кнопку следует нажимать несколько раз.

Рис. 2.3

Кнопка  – это оператор присвоения.

Кнопка if аналогична оператору условного перехода в языках Бейсик и Паскаль.

Кнопка otherwise дает возможность сделать выбор (аналог else в Бейсике и Паскале).

Кнопка for вводит в программу цикл с параметром (когда заранее известно, сколько циклов необходимо выполнить).

Кнопка while – образует заголовок цикла с предусловием. Такой цикл используется, если мы заранее не знаем, сколько циклов нам необходимо сделать для решения задачи.

Приступим к созданию компьютерной модели. Для начала зададим функцию и построим ее график в среде Mathcad (см. рис. 2.4).

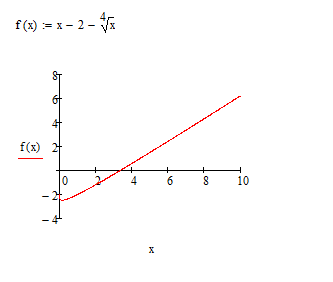
Рис.2.4

Как видно из чертежа, отделение корня было произведено верно. Далее составим наш алгоритм (см. рис. 2.5).

Рис. 2.5

Таким образом, решением нашего уравнения является число 3,352 (с точностью 0,01). Решение получено на 8-м шаге. Построим модель решения методом секущих (см. рис. 2.6).

Рис. 2.6.

Получили корень такой же точности, однако, уже на 3 шаге и он отличается на одну тысячную. Далее выясним, какое значение наиболее близко к корню. Рассмотрим, наконец, метод касательных (см. рис. 2.7).

Рис. 2.7.

Решение было получено такое же, как и предыдущим методом, и также на 3 шаге. Здесь мы воспользовались инструментом Mathcad – нахождение производной: оператор .

 

2.4. Эксплуатация и тестирование модели

В Mathcad есть вcтроенная функция root, которая позволяет найти решение одного уравнения с одним неизвестным с начальным приближением. Обращение к функции осуществляется следующим образом:

root(f(x),x), где f(x) – непосредственно само уравнение, x – аргумент, варьируя который, система ищет значение, обращающее в нуль заданное уравнение.

Воспользуемся данной функцией для нахождения решения нашего уравнения и сравним со значением, полученным на предыдущем шаге (см. рис. 2.8)

Рис. 2.8

Как мы видим, значение отличается на одну тысячную от значения, полученного численным методом, и совпадает со значением, которое было найдено методом секущих и касательных. Зададим точность и протестируем метод половинного деления (см. рис. 2.9).

Рис. 2.9

Получили ответ 3,353. Стоит заметить, что количество итераций, так же как и точность, увеличилось. Mathcad выводит ответ в виде таблицы, так как количество столбцов стало больше 10: ответ получен на 11 шаге.

Попробуем найти решение другого уравнения (см. рис. 2.10-2.13).

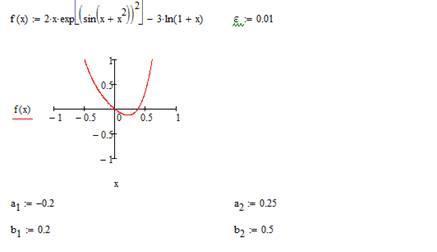
Рис. 2.10

Рис. 2.11

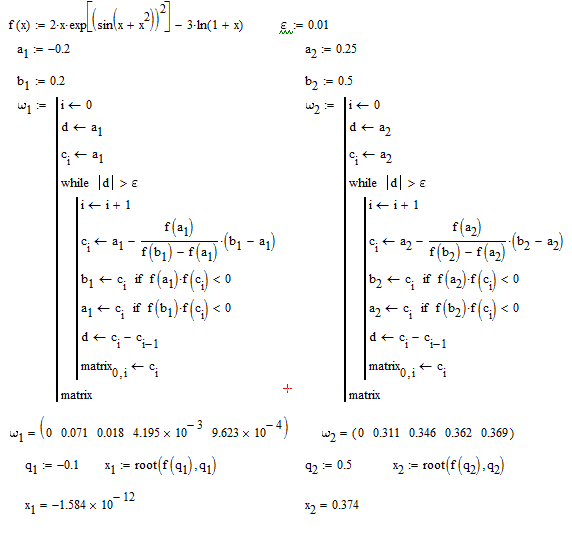
Рис. 2.12

Рис. 2.13

Можно видеть, в этом случае и методы секущих и касательных дают не такой точный результат, как функция нахождения корня root. Попробуем увеличить точность до 0,001 (см. рис. 2.14-2.16).

Рис. 2.14

Рис. 2.15

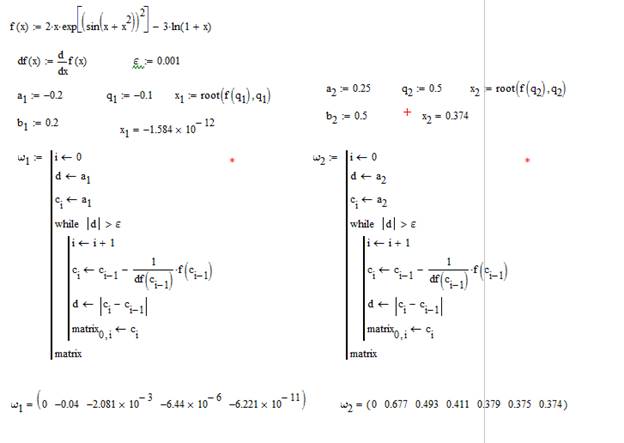
Рис. 2.16

 

 

2.5. Выводы и рекомендации по данной модели

Для данного уравнения было найдено решение в среде Mathcad численными методами: метод половинного деления, метод секущих и метод касательных – и с использованием стандартной функции. Методы секущих и касательных показали большую эффективность даже при относительно большой погрешности. Однако с усложнением функции и для них потребовалось увеличить точность, чтобы получить значение, наиболее близкое к решению уравнения. С увеличением точности время выполнения расчетов не изменилось, но мы получили наиболее близкий к истине ответ.

Данная модель может найти решение для любого нелинейного уравнения от одной переменной, в том числе, имеющего более одного корня. Причем, численный метод можно применять с различной долей погрешности.

 

2.6. Методические рекомендации для школьных учителей информатики

Среду Mathcad можно использовать как связующее звено между дисциплинами: математика, физика и информатика. Наиболее любознательные учащиеся сталкиваются при изучении математики и физики с характерной трудностью – недостатком математических знаний. Огромное число интересных задач, физическое содержание которых понятно, не могут быть решены, поскольку требуют знания производной, интеграла или дифференциальных уравнений. Например: учащиеся еще в 9-м классе знакомятся со вторым законом Ньютона и законом всемирного тяготения, однако этого недостаточно для расчета движения планет и космических кораблей. Хотя программой для физико-математических классов и предусмотрено изучение основ математического анализа, однако, в средней школе вряд ли возможно овладеть техникой вычисления интегралов и решения дифференциальных уравнений в той степени, которая необходима для решения физических задач. Да и при наличии соответствующих знаний нужно иметь ввиду, что подавляющее большинство интегралов не вычисляются через элементарные и специальные функции, а аналитическое решение известно лишь для некоторых классов дифференциальных уравнений.

Такие задачи можно рассматривать на уроке информатики. Учащиеся смогут проследить неразрывную связь изучаемых ими дисциплин, оценить одну из задач ЭВМ – автоматизация труда, повышение эффективности научных исследований.

Возможности MathCAD позволяют строить графики зависимостей, графически отделять корни уравнений, решать уравнения и системы уравнений, преобразовывать полученные выражения, проверять правильность полученного приближённого решения.

Нельзя забывать, что в приложении Mathcad школьники используют и программирование. Синтаксис схож с Pascal, Basic, поэтому составлять программы у учащихся не составит труда. Также, в связи с особенностью определения переменных в данной среде, можно наглядно объяснить различия между локальной и глобальной переменными.

Заключение

В заключение следует сказать, что тема «Численные методы решения уравнений в среде Mathcad» оказалась весьма интересной, а полученные знания будут полезны в дальнейшем обучении и практической деятельности. В ходе исследования были решены следующие задачи:

1.                 Были рассмотрены основные теоретические, методические моменты по разделу «Компьютерное моделирование». Также были проанализирована соответствующая документация, позволяющая определить требования к изучению компьютерного моделирования в школе.

2.                 Был проанализирован ряд программных сред и языков программирования для изучения темы «Компьютерное моделирование»: Turbo Delphi, Visual Basic, Maple, MathCad, Cinema 4D, Autodesk 3ds Max, SketchUp Make, Sweet Home 3D.

3.                 Была разработана компьютерная модель решения уравнений методом половинного деления в среде Mathcad.

Таким образом, цель курсовой работы достигнута, путем поэтапного решения поставленных задач.

Обобщая всё выше сказанное, отметим, что вопрос «Численные методы решения уравнений в среде Mathcad» обладает широким потенциалом для дальнейших исследований и практических изысканий.

 

 

Список литературы

1.                 Богданова, М. В. Особенности преподавания компьютерного моделирования в средней школе / М. В. Богданова, Е. В. Рощупкина // Молодой ученый. — 2017. — № 44 (178). — С. 152-155.

2.                 Босова, Л.Л, Босова, А.Ю. Информатика. 9 класс : учебник / Л.Л. Босова, А.Ю. Босова. – Москва : БИНОМ. Лаборатория знаний, 2016. – 208 с.

3.                 Босова, Л.Л. Информатика. 11 класс. Базовый уровень / Л.Л. Босова, А.Ю. Босова. – Москва : БИНОМ. Лаборатория знаний, 2017. – 256 с.

4.                 Гейн А.Г. Информатика. 10 класс. Базовый уровень : учебник

5.                 Горностаева Т.Н, Горностаев О.М. Компьютерное моделирование в школьном и вузовском курсе информатики / Т.Н. Горностаева, О.М. Горностаев // Мир науки. Педагогика и психология. – 2019. – №6.

6.                 Ершов, А.П. Основы информатики и вычислительной техники. Части 1, 2. Пробное учебное пособие для средних учебных заведений / А.П. Ершов, В.М. Монахов, С.А. Бешенков, Я.Э. Гольц, А.А. Кузнецов, Э.И. Кузнецов, М.П. Лапчик, А.С. Лесневский, Ю.А. Первин, Д.О. Смекалин. Под редакцией А.П. Ершова и В.М. Монахова. – Москва: Издательство «Просвещение», 1985. – 139 с.

7.                 Лапчик М.П. и др. Методика преподавания информатики: Учеб. Пособие для студ. Пед. Вузов / М.П. Лапчик, И.Г. Семакин, Е.К. Хеннер; Под общей ред. М.П. Лапчика. – М.: Издательский центр «Академия», 2001. – 624с.

8.                 Макарова, Н.В, Нилова, Ю.Н. Моделирование средствами языка программирования как технология системно-деятельностного подхода в обучении // Педагогическое образование в России. 2012. №5.

9.                 Поляков, К.Ю. Информатика. Углубленный уровень : учебник для 11 класса : в 2 ч. Ч.1 / К.Ю. Поляков, Е.А. Еремин. – Москва : БИНОМ. Лаборатория знаний, 2013. – 240 с.

10.            Поляков, К.Ю., Еремин, Е.А. Информатика. 9 класс / К.Ю. Поляков, Е.А. Еремин. – Москва : БИНОМ. Лаборатория знаний, 2017. – 288 с.

11.            Примерная основная образовательная программа основного общего образования от 28 июня 2016 г. №2/16-з.

12.            Примерная основная образовательная программа среднего общего образования от 8 апреля 2015 г. №1/15 (в ред. протокола №1/20 от 04.02.2020).

13.            Программно-методическое обеспечение профильного обучения по информатике и ИКТ. Тема 10. Моделирование и формализация. – URL: http://profil-ikt.narod.ru/modelirov/urok_10.htm

14.            Семакин, И.Г. Информатика : учебник для 8 класса / И.Г. Семакин, Л.А. Залогова, С.В. Русаков, Л.В. Шестакова – Москва : БИНОМ. Лаборатория знаний, 2015. – 176 с.

15.            Семакин, И.Г. Информатика. Базовый уровень : учебник для 11 класса / И.Г. Семакин, Е.К. Хеннер, Т.Ю. Шеина – Москва : БИНОМ. Лаборатория знаний, 2014. – 224 с.

16.            Семакин, И.Г. Информатика. Углубленный уровень : учебник для 11 класса : в 2 ч. Ч. 2 / И.Г. Семакин, Е.К. Хеннер, Л.В. Шестакова – Москва : БИНОМ. Лаборатория знаний, 2014. – 216 с.

17.            Федеральный государственный образовательный стандарт основного общего образования от 17 декабря 2010 г. №1897 (в ред. Приказа Минобрнауки России от 29.12.2014 №1644).

18.            Федеральный государственный образовательный стандарт среднего общего образования от 6 октября 2009 г. №413 (в ред. Приказа Минобрнауки России от 29.12.2014 №1645).

19.            Федеральный перечень учебников, допущенных к использованию и реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования организациями, осуществляющими образовательную деятельность от 20 мая 2020 г. №254.

 

 

Скачано с www.znanio.ru