Формула Эйлера в пространстве H3 с участием эллиптического трингла

© О.С. Басаргин

1. Постановка задачи

Построить аналог формулы Эйлера для произвольного (не изотропного) вектора v⃗ ∈ H₃, в котором одновременно участвуют:

•       ∣v⃗∣ — модуль вектора в H₃;

•       β — бингл между v⃗ и вещественной осью;

•       Σ_ell — эллиптический трингл, определяемый как длина дуги пересечения двух кубических сфер из противолежащих октантов пространства H₃.

2. Базис в пространстве H₃

Пусть v⃗= (x1, x2, x3) ∈ H₃ =R³. Кубическая метрика на H₃ задаётся как:

Модуль вектора определяется как:

предполагая, что M(v⃗) > 0.

3. Бингл: бинарный угол

Бингл между вектором v⃗и вещественной осью e₁ = (1,0,0) можно определить через нормированное кубическое полипроизведение:

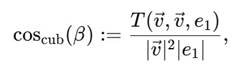
где T(u, v, w) = u₁v₂w₃ +… — кубическая форма.

1

4.                 Эллиптический трингл Σell Пусть заданы две кубические сферы:

 расположенные в противоположных октантах. Их пересечение определяет замкнутую дугу Γ на общей индикатрисе. Тогда длина этой дуги в фазовом параметре определяется как:

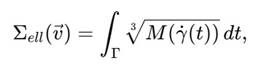
 где γ(t) ∈ S₁ ∩ S₂.

5.                 Формула Эйлера в H₃ (обобщённая) Предлагаемый вид формулы:

 где:

•       i_β и j_Σ — операторы вращения в пространстве бингла и трингла соответственно (аналог мнимой единицы);

•       exp_H3 — обобщённая экспонента в фазовом пространстве H₃, действующая как фазовый сдвиг по двум инвариантам.

6. Интерпретация

•       ∣v⃗∣ задаёт масштаб или модуль действия;

•       β — фазовое отклонение от реальной оси (аналог аргумента комплексного числа);

•       Σ_ell — глубинная «фазовая протяжённость» или вложенная кривая между симметричными фазами.

7. Заключение

Предложенная формула объединяет три типа инвариантов в пространстве H₃:

модуль (масштаб), бингл (фаза) и эллиптический трингл (структурная развёртка). Это потенциальная основа для новой фазовой динамики в трёхмерной метрике с кубической симметрией.

Формула может служить аналогом классической формулы Эйлера, но в терминах трёхмерного фазового пространства, где взаимодействуют направления, вложенности и фазовые геодезические структуры.

2