Сфираль и трингл: трёхмерная фаза и геометрия H₃

© О.С. Басаргин

Аннотация

В статье проводится сопоставление топологической модели Сфирали — зеркально-антисимметричной структуры, разворачивающейся в фазовом времени — с понятием трингла, введённого Д.Г. Павловым как третий метрический инвариант в пространстве тройных чисел H₃ = R ⊕ R ⊕ R.

Исследование основано на алгебре тройных чисел и кубической метрике третьего порядка, в которой появляются новые геометрические инварианты — бингл и трингл, определяющие относительное положение векторов в неквадратичной фазовой метрике. Сфираль интерпретируется как геодезическая траектория в пространстве H₃, развёрнутая через три направленных фазовых вектора, аналогичных вершинам геодезического треугольника на индикатрисе.

Показано, что трингл выражает вложенность, фазовую антисимметрию и Sсоединение между витками Сфирали. Построены условия геодезичности и предложена параметризация Сфирали как интегральной линии в метрике с фазовой скрученной симметрией. Таким образом, Сфираль получает строгую метрическую интерпретацию как фигура трёхфазного взаимодействия, не редуцируемого к длине и углу.

Статья открывает перспективы применения трингла и фазовой метрики к моделям времени, биодинамики, ритмической синхронизации и когнитивной геометрии.

1. Введение

1.1. Постановка задачи

Современные геометрические и алгебраические модели пространства и времени требуют пересмотра базовых понятий метрических инвариантов, особенно в контексте многомерных и неклассических структур. В настоящем исследовании ставится цель:

выявить соответствие между структурой Сфирали — зеркальноантисимметричного вложенного топологического образования — и понятием тринґла, предложенного Д.Г. Павловым и соавторами как третьего метрического инварианта в пространстве тройных чисел H₃ = R ⊕ R ⊕ R.

1.2. Актуальность

Понятие тринґла (трёхгранного угла) возникает в геометрии с кубической метрикой, где инварианты не ограничиваются длиной и углом, а определяются взаимодействием трёх векторов. Такая геометрия требует нового подхода к описанию топологических переходов, фазовых различий и структур вложенности. Одновременно, модель Сфирали была предложена как описание времени, разворачивающегося в поперечном направлении с фазовой обратимостью, что находит параллели в геометрии H₃.

1.3. Цель исследования

Настоящее исследование направлено на:

•       формализацию структуры Сфирали в терминах метрических инвариантов пространства H₃;

•       сопоставление витков Сфирали с направленными векторами, образующими тринґл;

•       выявление геометрических условий, при которых Сфираль реализуется как геодезическая траектория в псевдофинслеровом пространстве с кубической метрикой;

•       анализ фазовой вложенности как выражения метрического трёхкомпонентного взаимодействия.

1.4. Методология

Исследование опирается на:

•       материалы журнала «Гиперкомплексные числа в геометрии и физике» (2004–2011 гг.),

•       статьи Д.Г. Павлова, Г.И. Гарасько, С.В. Лебедева и др.,

•       теорию тройных чисел и трёхмерной метрики H₃,

•       введённые в этих работах инварианты: длина, бингл (двойной угол), трингл (трёхгранный угол),

•       сопоставление с авторской моделью Сфирали как структуры, выражающей фазовую антисимметрию и вложенность.

1.5. Структура работы

В последующих разделах будут рассмотрены:

•       краткий обзор теории тройных чисел и кубической метрики;

•       определение трингла как инварианта на индикатрисе в пространстве H₃;

•       формализация Сфирали как фазовой структуры и её параметризация;

•       сопоставление витков Сфирали с вершинами трёхгранной структуры;

•       обсуждение результатов и направления дальнейшего анализа.

2. Алгебра тройных чисел и кубическая метрика

2.1. Структура алгебры H₃ = R ⊕ R ⊕ R

Алгебра H₃ представляет собой прямую сумму трёх вещественных компонент. Элемент z ∈ H₃ записывается в виде:

или как линейная комбинация по базису {e₁, e₂, e₃}:

Алгебра коммутативна, ассоциативна и допускает полилинейные метрические формы третьего порядка.

2.2. Кубическая метрика

В отличие от классической евклидовой метрики:

в H₃ используется метрика третьего порядка (кубическая форма):

Это выражение инвариантно при перестановке компонент и определяет масштаб геодезических фигур (например, площадей на индикатрисе).

2.3. Индикатриса и геометрия

Единичная поверхность в H₃ определяется уравнением:

Это поверхность третьего порядка, называемая индикатрисой. Она играет ту же роль, что и сфера в евклидовой геометрии: на ней определяются углы, площади и геодезические фигуры.

2.4. Полилинейные инварианты В геометрии H₃ возникают:

•       бингл — аналог угла между двумя векторами,

•       трингл — новый инвариант, определяемый тройкой векторов, не сводящийся к длинам и обычным углам.

Эти величины описываются как геодезические величины на индикатрисе, и вместе с длиной формируют полную систему трёх метрических инвариантов для пространства H₃.

2.5. Значение для модели Сфирали

Кубическая метрика позволяет интерпретировать вложенность и антисимметрию Сфирали как векторное взаимодействие трёх фазовых направлений, в отличие от классических моделей времени. Это делает алгебру H₃ естественным кандидатом для формализации структуры Сфирали.

3. Трингл как метрический инвариант в пространстве H₃

3.1. Понятие трингла

Трингл — это третий независимый метрический инвариант пространства H₃ = R ⊕ R ⊕ R, который не может быть выражен через длины и углы. Он возникает в геометрии с кубической метрикой и определяется как инвариантная мера, ассоциированная с тремя векторами A, B, C в трёхмерной алгебре.

3.2. Геометрическое определение

Формально трингл Σ(A, B, C) определяется как площадь геодезического треугольника на индикатрисе — поверхности M(v) = 1 в пространстве с кубической метрикой. Трингл можно рассматривать как аналог телесного угла, но в более общем пространстве с неквадратичной метрикой.

3.3. Символическая форма

В работах Д.Г. Павлова и Г.И. Гарасько трингл связывается с тождествами кубического полипроизведения:

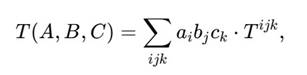
где T^ijk — симметричный тензор третьего порядка, отражающий свойства метрики пространства.

3.4. Свойства трингла

•       Трингл:

o не редуцируется к длинам и обычным углам, o зависит от трёх направлений одновременно, o сохраняется при конформных преобразованиях индикатрисы, o играет роль трёхгранного фазового инварианта.

•       При переходе к квадратичной метрике (например, евклидовой) трингл вырождается, т.е. исчезает как независимая величина.

3.5. Значение в модели Сфирали

В контексте Сфирали трингл может рассматриваться как мера фазовой развёртки трёх витков, связанных через зеркальные антисимметрии и вложенность. Он позволяет формализовать ту часть структуры, которая в двумерной алгебре не имела аналитического выражения, но была топологически осмыслена как переход и синхронизация витков.

3.6. Вывод

Трингл предоставляет математическую основу для описания вложенных, взаимно ориентированных фазовых направлений. Это делает его естественным кандидатом для отображения внутренней логики Сфирали в геометрических терминах. Следующий шаг — сопоставление витков Сфирали с вершинами геодезического треугольника, порождающего трингл.

4. Сфираль как треугольник трингла: фазовая развёртка в H₃

4.1. Постановка соответствия

В модели Сфирали фундаментальной единицей является триада витков: два зеркально-антисимметричных витка и связующее их S-соединение. Такая триада естественно сопоставляется с тремя векторами в пространстве H₃, образующими геодезический треугольник, на котором определяется трингл Σ(A, B, C).

4.2. Геометрическая интерпретация витков Пусть:

•       A — первый виток (в направлении «вперёд»),

•       B — второй виток (антисимметричный, в направлении «назад»),

•       C — вектор S-соединения (топологический скачок).

Каждый из этих векторов рассматривается как элемент H₃:

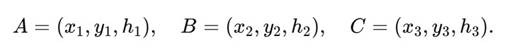
 Здесь x — направленность во времени, y — фаза, h — уровень вложенности.

4.3. Треугольник на индикатрисе

На единичной поверхности индикатрисы M(v) = 1, определённой кубической метрикой, три вектора A, B, C образуют замкнутый геодезический треугольник. Его площадь (в метрике третьего порядка) и есть значение трингла:

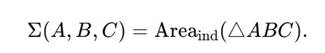
Это значение сохраняется при фазовых преобразованиях и отражает фазовую развёртку системы трёх витков.

4.4. Сопоставление с моделью Сфирали

4.5. Физико-фазовая трактовка

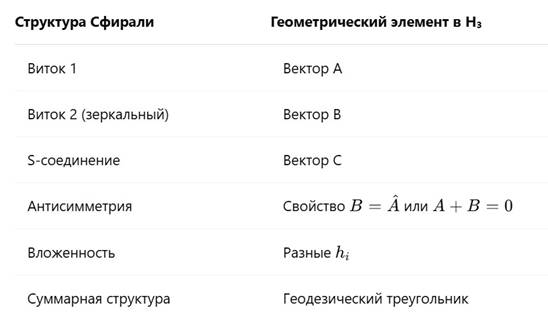
Сфираль как модель времени разворачивается не линейно, а по вложенной фазовой структуре. Трингл, как обобщённый трёхгранный угол, отражает именно это: взаимную направленность трёх фазовых векторов, которые нельзя описать через длину и угол попарно.

4.6. Вывод

Сфираль может быть интерпретирована как треугольник на индикатрисе пространства H₃, где каждый виток — это направленное событие, а их взаимное расположение задаёт значение трингла. Таким образом, Сфираль — не просто линия, а минимальная трёхфазная геодезическая структура, выражаемая через трёхкомпонентную метрическую форму.

5. Фазовая метрика и геодезическая Сфираль в пространстве H₃

5.1. Цель раздела

Построить условия, при которых Сфираль может быть интерпретирована как геодезическая траектория в трёхмерном пространстве H₃, снабжённом кубической фазовой метрикой, и формализовать саму метрику, описывающую такую геометрию.

5.2. Кубическая метрика

В отличие от квадратичных римановых форм, кубическая метрика определяется на тройках векторов и может быть записана как симметричная форма третьего порядка:

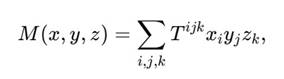
где T^ijk — полностью симметричный тензор метрики, отражающий свойства пространства H₃.

Для фазовой интерпретации удобно зафиксировать представление:

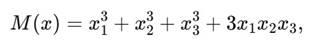
которое задаёт индикатрису M(x) = 1 и определяет скрученную геометрию.

5.3. Параметризация фазовой Сфирали Рассмотрим параметрическую кривую:

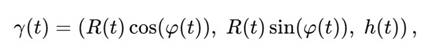
где:

•       R(t) = R₀α^t — радиус вложенности,

•       φ(t) — фазовый угол (с антисимметрией: φ_t+1 = −φ_t), •            h(t) — высота вложенности (обычно: h = h₀ + α^t).

Эта кривая описывает развёрнутую фазовую структуру Сфирали в координатах пространства H₃.

5.4. Условие геодезичности

Кривая γ(t) будет геодезической, если она экстремизирует кубическую длину, т.е. является решением вариационного уравнения для действия вида:

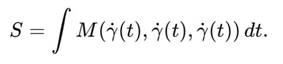
Тогда γ(t) удовлетворяет кубическим аналогам уравнений Эйлера–Лагранжа в H₃.

5.5. Свойства геодезической Сфирали

•       Она развивается не по минимальному расстоянию, а по минимальной фазовой скрученности,

•       Локальные скачки направления (фазовая инверсия) реализуют Sсоединения,

•       Вложенность отражается в постепенном изменении третьей координаты h(t),

•       Вся траектория укладывается в симметрию, допускающую инвариант трингла как фазовый объём.

5.6. Вывод

Сфираль может быть рассмотрена как геодезическая в фазовой геометрии H₃ с кубической метрикой. Её структура отражает не расстояние, а фазовую развёртку, вложенность и антисимметрию. Это открывает путь к описанию динамики Сфирали через кубическое варьирование и фазовую метрику, а не через классическую логику движения.

6. Заключение: Сфираль и трингл как единая геометрическая структура

6.1. Сводка результатов

В ходе настоящего исследования была осуществлена попытка геометрической и аналитической интерпретации структуры Сфирали в терминах метрической теории тройных чисел и фазового пространства с кубической метрикой.

•       Показано, что три витка Сфирали — два зеркальных и одно Sсоединение — могут быть сопоставлены с тремя векторами, определяющими трингл Σ(A, B, C) на индикатрисе.

•       Установлено, что трингл выражает метрическое взаимодействие трёх направлений, не сводимое к длинам и углам — и этим аналогичен топологической связности Сфирали.

•       Параметризация Сфирали в координатах H₃ и её развёртка в фазовом времени естественно согласуется с геодезическими кривыми в пространстве с кубической метрикой.

•       Введена формулировка фазовой метрики и условия геодезичности для Сфирали как фазовой траектории с вложенной антисимметрией.

6.2. Смысловое соответствие

6.3. Вывод

Сфираль и трингл могут быть поняты как разные языки описания одной и той же фундаментальной структуры — структуры трёхфазного взаимодействия, не редуцируемого к парным отношениям. Там, где Сфираль выражает топологическую динамику, трингл задаёт её геометрическую метрику.

Это сопоставление позволяет:

•       задать динамику времени и переходов через фазовую метрику,

•       расширить категорию событий до вложенных антисимметричных триад,

•       объединить подходы когнитивной модели времени и геометрической теории поля.

6.4. Перспективы

1. Формализация фазовых уравнений движения в пространстве H₃; 2. Визуализация трингловых развёрток как трёхмерных моделей Сфирали;

3.     Сопоставление с биометрикой (ДНК, ритмы, нейрополевая активность);

4.     Расширение к пространствам четверного порядка (H₄) и множественным фазовым инвариантам.

Исследование демонстрирует, что понятие Сфирали получает строгую математическую основу в геометрии трёхкомпонентных чисел и может рассматриваться как форма трингла — метрики различия трёх направлений внутри времени и пространства.

Используемая литература

1.     Павлов Д.Г. (2004). Обобщение аксиом скалярного произведения. // Гиперкомплексные числа в геометрии и физике, №1(1), с. 5–19.

2.     Павлов Д.Г. (2004). Хронометрия трёхмерного времени. // Гиперкомплексные числа в геометрии и физике, №1(1), с. 20–32.

3.     Гарасько Г.И., Павлов Д.Г. (2007). Геометрия невырожденных поличисел. // Гиперкомплексные числа в геометрии и физике, №4(1(7)), с. 3–25.

4.     Лебедев С.В. (2004). Свойства пространств, связанных с коммутативноассоциативными алгебрами H₃ и H₄. // Гиперкомплексные числа в геометрии и физике, №1(1), с. 68–74.

5.     Павлов Д.Г., Кокарев С.С. (2008). Конформные калибровки геометрии Бервальда–Моора. // Гиперкомплексные числа в геометрии и физике, №5(2(10)), с. 3–14.

6.     Павлов Д.Г. (2010). Гиперболический аналог электромагнитного поля. // Гиперкомплексные числа в геометрии и физике, №7(1(13)), с. 3–15.

7.     Павлов Д.Г., Кокарев С.С. (2011). Аналитические, дифференциальногеометрические и алгебраические свойства гладких функций поличисловой переменной. // Гиперкомплексные числа в геометрии и физике, №8(16).

8.     Зарипов Р.Г. (2006). Отношение одновременности в финслеровом пространстве-времени. // Гиперкомплексные числа в геометрии и физике, №3(5), с. 27–46.

9.     Сипаров С.В. (2005). Канонические уравнения Гамильтона и метрика Бервальда–Мура. // Гиперкомплексные числа в геометрии и физике, №2(4), с. 51–55.

10. Павлов Д.Г. (2004). Четырёхмерное время. // Геон-2003, Казань; также в: Гиперкомплексные числа в геометрии и физике, №1(1), с. 33–42.

11. Басаргин О.С. (2025). Эталонное описание устройства Сфираль. Zenodo. https://doi.org/10.5281/zenodo.15133508