Действия с векторами, нахождение элементов.

Практическая работа

 

Раздел 7. Координаты и векторы

Тема. "Действия с векторами, нахождение элементов".

 

Учебная цель: продолжить формирование знаний, обучающихся по данной теме.

 

Учебные задачи:

Обучающая: Ввести определения вектора в пространстве, равенства векторов. Рассмотреть правила треугольника и параллелограмма сложения векторов в пространстве, правило вычитания векторов, правило сложения нескольких векторов в пространстве.

Воспитательная: Воспитывать личностные качества обучающихся (умение слушать), доброжелательность по отношению к окружающим, внимательность, аккуратность, дисциплинированность. Воспитывать интерес к предмету и потребности в приобретении знаний.

Развивающая: Развивать пространственное воображение и логическое мышление обучающихся, умение быстро ориентироваться в обстановке; развивать сообразительность, находчивость, тренировать память.

 

Обеспеченность занятия:

 

1.Учебно-методическая литература:

·         Л.С. Атанасян и др., Геометрия. 10-11 кл. – М.: Просвещение, 2014.

2.Рабочая тетрадь: в клетку

3.Раздаточные материалы (карточки-задания, по количеству обучающихся).

4.Калькулятор: простой.

5.Ручка.

6.Карандаш простой.

7.компьютер,

8.мультимедийный проектор,

9.экран.

 

Краткие теоретические и учебно-методические материалы по теме практической работы.

 Сложение векторов, умножение вектора на число

В окру­жа­ю­щем мире мы встре­ча­ем­ся с та­ки­ми ве­ли­чи­на­ми, для ко­то­рых важен не толь­ко раз­мер, но и на­прав­ле­ние. Та­ки­ми ве­ли­чи­на­ми яв­ля­ют­ся, на­при­мер, сила и ско­рость. В ма­те­ма­ти­ке такие ве­ли­чи­ны опи­сы­ва­ют­ся век­то­ра­ми.

Век­тор – на­прав­лен­ный от­ре­зок.

Век­тор  (рис. 1).

Кол­ли­не­ар­ны­ми век­то­ра­ми на­зы­ва­ют­ся такие век­то­ры, ко­то­рые лежат на па­рал­лель­ных пря­мых либо на одной пря­мой.  (рис. 2).

Рис. 2. Кол­ли­не­ар­ные век­то­ры

Можно вве­сти такое число , при ко­то­ром  (рис. 3). То есть умно­же­ни­ем век­то­ра на ка­кое-ли­бо число , можно рас­тя­нуть или сжать век­тор.

Рис. 3. Умно­же­ние век­то­ра на число

Если век­то­ры кол­ли­не­ар­ные и со­на­прав­лен­ные и их длины равны, то такие век­то­ры на­зы­ва­ют­ся рав­ные: .

Сложение векторов:

1. Пра­ви­ло па­рал­ле­ло­грам­ма (рис. 4).

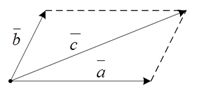
Рис. 4. Сло­же­ние век­то­ров

2. Пра­ви­ло тре­уголь­ни­ка (рис. 5).

 

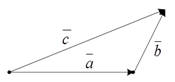
Рис. 5. Сло­же­ние век­то­ров

 Векторы в пространстве

Рас­смот­рим век­то­ры в про­стран­стве. Для этого необ­хо­ди­мо вы­брать три неком­пла­нар­ных век­то­ра (.

Тео­ре­ма: в про­стран­стве любой век­тор можно раз­ло­жить по трём дан­ным неком­пла­нар­ным век­то­рам, при­чём ко­эф­фи­ци­ен­ты раз­ло­же­ния опре­де­ля­ют­ся од­но­знач­но: . То есть век­тор  од­но­знач­но раз­ла­га­ет­ся по век­то­рам , ,  с по­мо­щью чисел x, y, z (эта трой­ка чисел од­но­знач­ная).

  Введение, понятие компланарности векторов

Век­то­ры на­зы­ва­ют­ся ком­пла­нар­ны­ми, если при от­кла­ды­ва­нии их от одной и той же точки они будут ле­жать в одной плос­ко­сти.

Рас­смот­рим век­то­ры  и : рис. 1

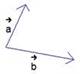
Рис. 1. Век­то­ры  и 

Мы знаем, что если за­да­ны два некол­ли­не­ар­ных век­то­ра на плос­ко­сти, то любой тре­тий век­тор на той же плос­ко­сти можно од­но­знач­но раз­ло­жить по этим век­то­рам: рис. 2, 3.

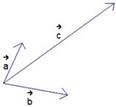
Рис. 2. Век­то­ры на плос­ко­сти

 Теорема о разложении вектора по двум неколлинеарным

 Теорема о компланарных векторах, сложение векторов в пространстве

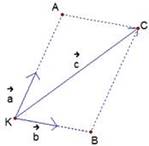
Если век­тор  можно пред­ста­вить в виде , где х и у – кон­крет­ные числа, то век­то­ра  и  ком­пла­нар­ны.

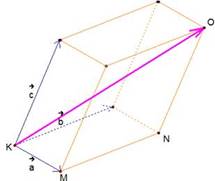
Рис. 4. Сло­же­ние век­то­ров в про­стран­стве

  Теорема о разложении вектора по трем некомпланарным векторам

Любой век­тор в про­стран­стве можно раз­ло­жить по трем за­дан­ным неком­пла­нар­ным век­то­рам, при­чем ко­эф­фи­ци­ен­ты раз­ло­же­ния опре­де­ля­ют­ся един­ствен­ным об­ра­зом:.  , где х, y, z – числа.

 

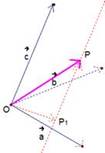
Рис. 5. Раз­ло­же­ние век­то­ра по трем неком­пла­нар­ным

 

Задания для практического занятия:

 

Задание 1

подготовка к работе на заняти:

- настрой на работу, организация внимания;

- проверка домашнего задания

- актуализация опорных знаний.

Задание 2

Фронтально с группой:

  1. Как называются векторы, имеющие равные модули и противоположно направленные?

А) противоположные

Б) противоположно направленные

В) равные

 

 

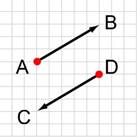
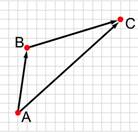
2. Тело переместили из точки А в точку В, а потом из точки В в точку С. Какой вектор представляет суммарное перемещение тела?

А)

Б)

В)

 

    

 

3. Закончите предложение:

Суммой двух векторов называется вектор, построенный по правилу.... (треугольника)

4. Вставьте пропущенное слово:

 Чтобы сложить два неколлинеарных вектора  и,  нужно отложить от произвольной точки О векторы  = и  = и построить .... ОАСВ, тогда  =+

 

(параллелограмм)

 

   5. Изображенный на рисунке способ построения суммы нескольких векторов называется правилом...

 

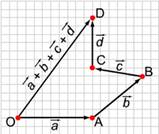
 (многоугольника)

 

Задание 3

Глава 4, §1, Стр. 84 Л.С. Атанасян и др., Геометрия. 10-11 кл. – М.: Просвещение, 2014. (Учебники выдает преподаватель)

Работа по учебнику.

а)Прочитать материал стр. 84-85. Записать основные определения  себе в тетрадь.

Работа в парах. Вопросы друг другу и преподавателю.

б) Определение стр. 85  разобрать у доски. Обсуждение. Записать в тетрадь.

Задание 4

Самостоятельно выполнить задания (с проверкой у доски – несколько человек)

№№ 320(а); 322

Задание 5

Сделать самостоятельно

№№ 320(б); 323

Дополнительно (индивидуально) тем, кто быстрее справится с заданиями: №326

Обсудить и проверить решения друг с другом.

Задание 6

Глава 4, §2, Стр. 87 Л.С. Атанасян и др., Геометрия. 10-11 кл. – М.: Просвещение, 2014. (Учебники выдает преподаватель)

Работа по учебнику.

а)Прочитать материал стр. 87-89. Записать основные определения  себе в тетрадь.

Работа в парах. Вопросы друг другу и преподавателю.

б) Правила стр. 87  разобрать у доски. Обсуждение. Записать в тетрадь.

в) Правила стр.88-89  разобрать у доски. Обсуждение. Записать в тетрадь.

Задание 7

Самостоятельно выполнить задания (с проверкой у доски – несколько человек)

№№ 328(а); 333(а); 335(а)

Задание 8

Сделать самостоятельно

№№ 328(б); 333(б); 335(б)

Дополнительно (индивидуально) тем, кто быстрее справится с заданиями: №347(а)

Обсудить и проверить решения друг с другом.

Задание 9

Глава 4, §3, Стр. 92 Л.С. Атанасян и др., Геометрия. 10-11 кл. – М.: Просвещение, 2014. (Учебники выдает преподаватель)

Работа по учебнику.

а)Прочитать материал стр. 92-95. Записать основные определения  себе в тетрадь.

Работа в парах. Вопросы друг другу и преподавателю.

б) Правила стр. 93  разобрать у доски. Обсуждение. Записать в тетрадь.

в) Теорему  стр.94  разобрать у доски. Обсуждение. Записать в тетрадь.

Задание 10

Самостоятельно выполнить задания (с проверкой у доски – несколько человек)

№№ 355(а, б); 358(а, б); 359(а)

Задание 11

Сделать самостоятельно

№№ 355(в); 358(в); 359(б)

Азобрать задачу 362. Обсуждение.

Дополнительно (индивидуально) тем, кто быстрее справится с заданиями: №376(а)

Обсудить и проверить решения друг с другом.

Задание 12

Подвести итог работы на занятии.

Записать домашнее задание.

Вопросы для закрепления теоретического материала к практическому занятию:

 

1.      Что называется направленным отрезком? Начало, конец, длина направленного отрезка?

2.      Что называется вектором? Их обозначение.

3.      Что называют длиной или модулем ненулевого вектора?

4.      Что называют направлением ненулевого вектора?

5.      Какой вектор называют единичным?

6.      Какой вектор называют нулевым?

7.      Какие векторы называют одинаково направленными, противоположно направленными?

8.      Какие векторы называются коллинеарными?

9.      Какие два вектора называются равными?

10.  Какие векторы называются противоположными?

11.  Что называется суммой двух векторов?

12.  Правило треугольника.

13.  Правило параллелограмма.

14.  Правило многоугольника.

15.  Правило параллелепипеда.

16.  Что называется разностью двух векторов?

 

Скачано с www.znanio.ru