
Проектная работа
Диагностическая работа
для учащихся 10 классов по теме
«Производная. Применение производной»
Выполнил: слушатель курсов повышения квалификации
«Методика подготовки учащихся к ГИА по математике»
Срок курсов с 26.11.18 по 01.12.18
Дергачева Татьяна Юрьевна, учитель МАОУ «СОШ № 10»
Спецификация работы
|
Проверяемое содержание |
Номер задания в работе |
|
|
Умение находить производную линейной функции |
1 |
|
|
Умение находить значение производной степенной функции в данной точке |
2 |
|
|
Умение находить скорость материальной точки в данный момент времени, используя физический смысл производной |
3 |
|
|
Умение находить значение производной функции в данной точка по графику |
4 |
|
|
Умение находить количество точек экстремума по графику производной функции |
5 |
|
|
Умение находить по графику производной функции промежутки возрастания или убывания функции и сумму целых чисел, входящих в эти промежутки |
6 |
|
|
Умение находить абсциссу точки касания графика функции и касательной |
7 |
|
|
Умение находить значение производной функции в данной точке |
8 |
|
|
Умение находить точку максимума или минимума функции |
9 |
|
|
Умение находить наибольшее или наименьшее значение тригонометрической функции |
10 |
Текст работы
Вариант № 1.
Инструкция по выполнению работы.
Работа состоит из двух частей. Часть 1 содержит 6 заданий обязательного уровня и часть 2 содержит 4 задания повышенного уровня по материалу курса «Алгебры и началам анализа» 10 класса. При решении заданий части 1 в бланк ответов вписывается ответ, получившийся в результате решения задания. Если Вы записали неверный ответ, аккуратно зачеркните его и рядом запишите другой ответ. Ответом на задания этой части должно быть целое число или число, записанное в виде конечной десятичной дроби.
Задания части 2 с развёрнутым ответом требуют записи полного решения с необходимым обоснованием выполненных действий.
За каждое верно выполненное задание части 1 Вы получаете 1 балл, за каждое задание части 2 – от 0 до 2 баллов.
Советуем для экономии времени пропускать задание, которое не удаётся выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у Вас останется время.
Желаем успехов!
Часть 1
1. Найдите производную функции ![]() .
.
2. Найдите значение
производной функции ![]() в точке х0 = -
1.
в точке х0 = -
1.
3. Материальная точка движется прямолинейно по закону x(t)=6t2 - 48t + 17, где x - расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t=9с.
4. На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной функции f(x) в точке х0.
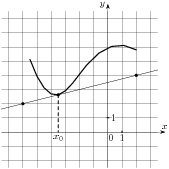
5. На рисунке изображен график производной функции f(х), определенной на интервале (- 19;5). Найдите количество точек экстремума функции f(х) на отрезке [ -15;2].

6. На рисунке изображен график y=f /(x) - производной функции f(x), определенной на интервале (-5;7). Найдите промежутки убывания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
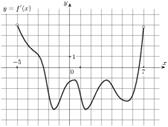
Часть 2
7. Прямая y= - 4x - 11 является касательной к графику функции
y= x2 + 7x - 6. Найдите абсциссу точки касания.
8. Найдите
значение производной функции у = ![]() в точке х0 = 10 .
в точке х0 = 10 .
9. Найдите точку минимума функции y=(x+3)2(x+5) -1
10. Найдите наибольшее значение функции у = 12х – 2sinх +
3 на отрезке [- ![]() ; 0] .
; 0] .
Вариант № 2.
Часть 1
1. Найдите производную функции ![]() .
.
2. Найдите значение производной функции ![]() в точке х0 = - 2.
в точке х0 = - 2.
3. Материальная точка движется прямолинейно по закону x(t)=t2 - 13t+23, где x - расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с?
4. На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной функции f(x) в точке х0.
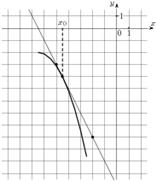
5. На рисунке изображен график производной функции f(x), определенной на интервале ( - 6;15) . Найдите количество точек экстремума функции f(x) на отрезке [ - 5;13].

6. На рисунке изображен график y=f /(x) - производной функции f(x), определенной на интервале (-7;4). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
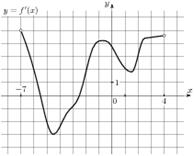
Часть 2
7. Прямая y = 7x - 5 параллельна касательной к графику функции
y= x2 + 6x - 8. Найдите абсциссу точки касания.
8. Найдите значение производной
функции ![]() в точке х0 = - 10.
в точке х0 = - 10.
9. Найдите точку максимума функции y=(x-2)2(x-4)+5
10. Найдите наименьшее значение функции у=2соsх +
5х + 8 на отрезке [0; ![]() ]
]
Ключ к работе
1 вариант.
|
Номер задания |
Правильный ответ |
|
1 |
6 |
|
2 |
- 2 |
|
3 |
60 |
|
4 |
0,25 |
|
5 |
5 |
|
6 |
18 |
|
7 |
- 5,5 |
|
8 |
- 0,02 |
|
9 |
- 3 |
|
10 |
3 |
2 вариант.
|
Номер задания |
Правильный ответ |
|
1 |
- 5 |
|
2 |
48 |
|
3 |
8 |
|
4 |
- 2 |
|
5 |
5 |
|
6 |
- 3 |
|
7 |
0,5 |
|
8 |
0,01 |
|
9 |
2 |
|
10 |
10 |
Критерии оценивания работы
Работа состоит из двух частей.
Каждое задание части 1 (1-6) оценивается в 1 балл.
Задание части 2 (7-10) оценивается от 0 до 2 баллов.
|
Баллы |
Критерии оценки выполнения задания части 2
|
|
2 |
Приведена верная последовательность всех шагов решения, вычисления выполнены верно, получен верный ответ. |
|
1 |
Приведена верная последовательность всех шагов решения, допущена описка и/или вычислительная ошибка, не влияющая на дальнейший ход решения. |
|
0 |
Все случаи решения, которые не соответствуют вышеуказанным критериям. |
Соотношение тестового балла и аттестационной отметки:
|
Тестовый балл |
Аттестационная отметка |
|
12-14 |
5 |
|
8-11 |
4 |
|
5-7 |
3 |
|
0-4 |
2 |
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.