Вяльшина Вера Константиновна

                                                                                                ГБПОУ РМ  «Саранский техникум

                                                                                                      пищевой и перерабатывающей

                                                                                                                             промышленности»

преподаватель математики

 г.Саранск  

 

ДИДАКТИЧЕСКАЯ ИГРА КАК СРЕДСТВО ПОВЫШЕНИЯ ИНТЕРЕСА

У СТУДЕНТОВ К ИЗУЧЕНИЮ МАТЕМАТИКИ

Без игры нет, и не может быть полноценного

 умственного развития. Игра – это огромное

                                                                                   светлое окно, через которое в духовный мир

                                                                                             ребенка вливается живительный поток

                                                                                        преставлений, понятий. Игра – это искра,

                                                                  зажигающая огонек пытливости и любознательности.

В.А. Сухомлинский

 Основная задача, которая стоит перед системой среднего профессионального образования – подготовка высококвалифицированного, конкурентно-способного специалиста. Для решения поставленной проблемы преподавателю необходимо проводить уроки в соответствии с требованиями  федерального государственного образовательного стандарта, использовать современные педагогические технологии и методы, активизирующие познавательную и мыслительную деятельность студентов, вовлекать студентов во внеурочную работу по предмету, заинтересовать их, показывая связь предмета с выбранной профессией.

Как показала практика, одни студенты интересуются математикой в силу необходимости для своей будущей работы, другие сомневаются, пригодятся ли им, вообще, знания по математике в их практической деятельности. Это заставляет задуматься над тем, как поддержать у студентов интерес к изучаемому материалу, их активность на протяжении всего урока. Возникновение интереса к математике у значительного числа студентов зависит в большей степени от того, насколько умело будет построена учебная работа.

               Может ли урок математики быть интересным? Может ли он активизировать творческие и познавательные силы студента? Может ли он, не только давать знания, расширяя кругозор студентов, но и ставить его перед ситуацией нравственного выбора, принятия им самостоятельного решения? Я считаю, что может и должен! И достичь этого можно решением занимательных задач и активизацией познавательно - игровой деятельностью на уроках.

             В математической литературе, в учебниках всегда уделялось большое внимание занимательным задачам, так как считалось, что элемент занимательности облегчает обучение. К занимательным относятся задачи с интересным содержанием или нетрадиционными формами решения. Решение занимательных задач способствуют развитию мыслительных операций. При выполнении таких заданий развивается интуиция, творчество, воспитывается усидчивость, развиваются различные виды памяти, пространственное и образное мышление.

В процессе же игры у студентов вырабатывается привычка сосредоточиваться, мыслить самостоятельно, развивается внимание, стремление к знаниям. Увлекшись,  дети не замечают, что учатся: познают, запоминают новое, ориентируются в необычных ситуациях, пополняют запас представлений, понятий, развивают фантазию. Даже самые пассивные из студентов включаются в игру с огромным желанием, прилагая все усилия, чтобы не подвести товарищей по игре.

           Что же такое игра?  В толковом словаре русского языка приводятся значения слова «играть». Игра определяется  как «действие по глаголу играть»: «развлекаться, забавляться…Проводить время в каком-либо занятии, служащим для развлечения, доставляющим удовлетворение, удовольствие одним только участием в нём».

          В последнее десятилетие в педагогической литературе появилось много определений игры. Например, учёные П.И. Пидкасистый и  Ж.С. Хайдаров давали ей такое определение: «Игра есть то, что задумано и сделано; то, что есть, что думает и о чём думает субъект, когда он действительно увлечён этой деятельностью с непременной установкой на очевидный всем результат». У Г.К. Селевко определение игры таково:  «Игра- это вид деятельности в условиях ситуаций, направленных на воссоздание и усвоение общественного опыта, в котором складывается и совершенствуется самоуправление поведением».

Известный французский ученый Луи де Бройль утверждал, что все игры (даже самые простые) имеют много общих элементов с работой ученого. В игре привлекает поставленная задача и трудность, которую можно преодолеть, а затем радость открытия и ощущение преодоленного препятствия. Именно поэтому всех людей, независимо от возраста, привлекает игра.

В отличие от игр вообще педагогическая игра обладает существенным признаком - четко поставленной целью обучения и соответствующим ей педагогическим результатом, которые могут быть обоснованы, выделены в явном виде и характеризуются учебно-познавательной направленностью.

         Цели дидактических игр при изучении математики:

-активизация мыслительной деятельности;

-развитие познавательных способностей;

-развитие логического мышления;

-способствование углублению знаний по математике;

-способствование восприятию межпредметных связей;

-привитие математической культуры;

-сплочение коллектива, формирование деловых взаимоотношений;

-развитие индивидуальности и коммуникативных способностей.

         Дидактические игры на уроках математики призваны решать следующие задачи.

Образовательные:

-способствовать прочному усвоению обучающимися учебного материала;

-способствовать расширению кругозора обучающихся и др.

Развивающие:

-развивать у обучающихся творческое мышление;

-способствовать практическому применению умений и навыков, полученных на уроках и внеклассных занятиях;

-способствовать развитию воображения, фантазии, творческих способностей и др.

Воспитательные:

-способствовать воспитанию саморазвивающейся и самореализующейся личности;

-воспитать нравственные взгляды и убеждения;

-способствовать воспитанию самостоятельности и воли в работе.

           Дидактические  игры при изучении математики выполняют различные функции.

1. Во время игры происходит одновременно игровая, учебная и трудовая деятельность. Действительно, игра сближает то, что в жизни не сопоставимо и разводит то, что считается едино.

2. Игра требует от студента, то чтобы он знал предмет. Ведь не умея решать задачи, разгадывать, расшифровывать и распутывать студент не сможет участвовать в игре.

3. В играх студенты учатся планировать свою работу, оценивать результаты не только чужой, но и своей деятельности, проявлять смекалку при решении задач, творчески подходить к любому заданию, использовать и подбирать нужный материал.

4. Результаты игр показывают студентам их уровень подготовленности, тренированности. Математические игры помогают в самосовершенствовании учащихся и, тем самым побуждают их познавательную активность, повышается интерес к предмету.

5. Во время участия в играх студенты не только получают новую информацию, но и приобретают опыт сбора нужной информации и правильного ее применения.

          Каждая дидактическая игра имеет правила, которые определяют порядок действий и поведение учащихся в процессе игры, способствуют созданию на уроке рабочей обстановки. Поэтому правила разрабатываю с учётом цели урока и индивидуальных возможностей студентов. Правила игры воспитывают умение управлять своим поведением, подчиняться требованиям коллектива.

 Дидактическая игра имеет определённый результат, который является финалом игры, придаёт игре законченность. Для меня результат игры всегда является показателем уровня достижений студентов или в усвоении знаний, или в их применении. Поэтому при подготовке к уроку, содержащему игру, составляю краткую характеристику хода игры (сценарий), указываю временные рамки игры, учитывая уровень знаний студентов, реализовываю межпредметные связи.

Игра для студентов 1-х и 2-х курсов является одной из самых привлекательных форм деятельности, и поэтому я стараюсь искать возможности применения её в подготовке студентов к усвоению важных математических идей, т.е. обучать математике в процессе игры.

         Мной разработана система дидактических игр для различных типов уроков, направленная на формирование учебно-познавательного интереса учащихся к математике.

Выделяю следующие виды дидактических игр:

- игры-упражнения;

-игры-путешествия;

-игры-соревнования;

-сюжетные (ролевые) игры.

Игры-упражнения.

          Они занимают обычно 10-15 минут и направлены на совершенствование познавательных способностей студентов, являются хорошим средством для развития познавательных интересов, осмысления и закрепления учебного материала, применения его в новых ситуациях. Это различные викторины, кроссворды, ребусы, чайнворды, шарады, головоломки, загадки. Дети сами охотно составляют кроссворды по различным темам, придумывают и разгадывают ребусы.

           В начале урока можно предложить ребятам, разгадав ребус или кроссворд, самим назвать тему занятия.

          Так, например, тема урока «Прямоугольный параллелепипед» может быть зашифрована в ребусе

А тема урока «Производная» - в ребусе

На первом занятии первого курса в процессе повторения теоретического материала за курс девятилетней школы можно предложить кроссворд:

 

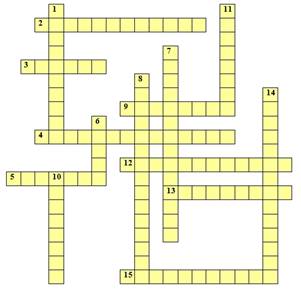
По горизонтали:

2. Прямые, которые лежат в одной плоскости и не пересекаются. (Параллельные)
3. Один из видов симметрии  Осевая)
4. Одна из моделей числового промежутка. (Геометрическая)
5. Неравенства вида х > а и х < а . (Строгие)
9. Слагаемые, которые отличаются только своими коэффициентами. (Подобные)
12. Прямая с указанными на ней началом отсчета, направлением отсчета и единичным отрезком. (Координатная)
13. Неравенства вида х ≥ а и х ≤ а . (Нестрогие)
15. Один из видов симметрии. (Центральная)
По вертикали:
1. Из всех общих кратных для чисел наибольшее значение имеет это. (Наименьшее)
6. Натуральные числа, числа им противоположные и число ноль. (Целые)
7. Треугольник, у которого две стороны равны. (Равнобедренный)
8. Числа, имеющие одинаковые модули, но отличающиеся знаком. (Противоположные)
10. Таким бывает луч .(Открытый)
11. Для терминов «луч», «отрезок», «интервал» есть общее название – … промежутки. (Числовые)
14. Когда составлено уравнение по условию задачи, то говорят, что составлена такая модель. (Математическая)

Игры-путешествия.

           Они служат для углубления, осмысления и закрепления учебного материала. Активизация студентов в таких играх выражается в устных рассказах, вопросах, ответах.

           Как известно, математика применяется практически во всех областях человеческой деятельности, в разных профессиях. Мы исследуем, как используются математические знания в кулинарии.

           Математика в кулинарии имеет большое значение, так как для приготовления любого блюда должен соблюдаться рецепт. В рецепте указывается точное соотношение продуктов, которое необходимо соблюдать в процессе приготовления. При взвешивании продуктов в кулинарии используются математические величины - масса и объём. Ими тоже необходимо уметь пользоваться. Единицы времени играют далеко не последнюю роль в приготовлении блюд. Приготовленные блюда нужно умело делить на порции, в чём нам опять же поможет математика.

          При подсчете калорийности готовых блюд учитываются её изменения при различных видах кулинарной обработки: варка, жарка, тушение, кипячение и др. Учитывается в обязательном порядке потеря белков, жиров, углеводов, витаминов и минералов при обработке и даже при нарезке продуктов. Учитывается потеря массы готового блюда и использование воды при приготовлении. Истинный повар должен обладать хорошей памятью, уметь быстро считать, и знать основные математические понятия: пропорция, проценты, уравнение.

            Часто со студентами заочно отправляемся в путешествия по разным странам, изучая их кухню. Решаем задачи с профессиональной направленностью, знакомимся со страной и развитием математики в этой стране.

Например, решаем следующую задачу:

 На приготовление японского блюда-суши израсходовано 140 г листовых морских водорослей, 210г риса, и 350 г рыбы. Сколько одинаковых роллов получилось?

Для решения задачи сперва следует определить наименьший общий делитель для веса каждого из ингредиентов.  В таком случае получим:

140 = 2 * 2 * 5 * 7,

210 = 2 * 3 * 5 * 7,

350 = 2 * 5 * 5 * 7.

НОД (140, 210, 350 ) = 2 * 5 * 7 = 70.

В таком случае получилось 70 одинаковых роллов, в каждом из которых было:

140 / 70 = 2 грамма водорослей.

210 / 70 = 3 грамма риса.

350 / 70 = 5 грамм рыбы.

Второй способ.

140 + 210 + 350 = 700 грамм продуктов.

2 + 3 + 5 = 10 грамм (Вес одного ролла.)

При общем весе равном 10 грамм, вышло:

700 / 10 = 70 роллов.

После решения «отправляемся» в Японию. Знакомимся с ее достопримечательностями и великими людьми.

Игры-соревнования.

            Для проведения этого вида игры студенты делятся на группы, команды, между которыми идёт соревнование. Существенной особенностью игры-соревнования является наличие в ней соревновательной борьбы и сотрудничества. Игра-соревнование позволяет мне в зависимости от содержания материала вводить в игру не просто занимательный материал, но весьма сложные вопросы учебной программы. Так, например, особо сложной для студентов является тема «Тригонометрические формулы». Поэтому я решила провести урок закрепления полученных знаний по данной теме в форме игры «Математический турнир».

        Группа делится на две команды, выбираются капитаны, придумываются девизы. Соревнование проходит в несколько туров.

Тур I - «Устные упражнения» В этом туре вопросы задаются по очереди обеим командам. Если ответ неправильный, может ответить другая команда. Количество баллов - количество верных ответов.

Тур II – «Вывод формул». В этом туре нужно вывести тригонометрическую формулу. На слайде    представлены картинки – анимации, на обратной стороне которых записаны тригонометрические формулы. От каждой команды выходят к доске по одному человеку. Выбирают картинку и выводят заданную формулу. Всего в этом туре участвуют 4 человека

( по 2 от каждой команды)

Тур III - «Индивидуальное задание».  Каждая команда делится на три группы. Первая группа получает конверт  с названием «Найти», вторая - конверт с названием «Вычислить», третья - конверт с названием «Упростить». В каждом конверте лежат листочки с заданием. Каждый учащийся берет одно задание, выполняет его и сдает на проверку. Количество баллов – количество верно выполненных заданий. Для защиты своего решения один учащийся из каждой команды выходит к доске и решает свое задание.

Тур IV - «Пасьянс». Пасьянс содержит 20 карточек, на которых написано 10 формул

приведения (левая часть до знака равенства на одной карточке, правая - на другой). Эти карточки раскладываются в 4 рада по 5 карточек в каждом ряду. Карточки можно брать по 2 либо по вертикали, либо по горизонтали. Каждая пара считается удачей, если она составляет формулу.

Тур V- «Конкурс капитанов». Капитанам предлагается пройти тест за компьютерами, причём задания в тестах одинаковые.

          В процессе проведения такого занятия идет глубокое закрепление изученного материала. У студентов развивается большой интерес к дисциплине, осваиваются компьютерные технологии, нарабатываются навыки общения, права добровольного участия. Работают все студенты, даже  неуверенные в своих знаниях.

Сюжетные (ролевые) игры.

         Такой урок удобнее всего проводить при повторении и обобщении темы.

В деловых играх на основе игрового замысла моделируются жизненные ситуации: игра представляет участнику возможность побывать в роли экскурсовода, преподавателя, судьи, директора и т.п. Использование деловых игр значительно укрепляет связь (студент – преподаватель), раскрывает творческий потенциал каждого обучаемого.

         Так, например, для закрепления темы «Круглые тела. Площади поверхностей круглых тел» мной был проведен урок – игра «Математик-бизнесмен». Группа делится на две команды - банки, которые, решая экономические вопросы, связанные с деньгами, прибылью, доходами, увеличивают свой первоначальный капитал. У них есть акционеры, которые, отвечая на вопросы, тоже будут приносить прибыль.

         Каждый банк выбирает своего управляющего, который имеет право принимать окончательное решение по данному вопросу.

Стартовый капитал каждого банка - 1000 р.

Каждому банку предлагается по очереди выбрать себе задание стоимостью от 50 до 200 р.

Если команда, представляющая данный банк, дает правильный ответ, то ее капитал увеличивается на стоимость задания.

Если ответ неправильный, то капитал уменьшается на:

а) 50% стоимости задания, если другой банк так же не сможет ответить верно;

б) на 100% стоимости задания, если другой банк дает правильный ответ, а команда, представляющая этот банк, получает прибавку к своему капиталу, равную 100% стоимости задания.

Команда может продать свое задание банку по взаимному согласию, при решении задания ее капитал увеличивается на стоимость задания.

Время на обдумывание задания предоставляется в зависимости от его сложности.

Стоимость задания         50 р       100 р            150 р              200 р

Время                               30 с     1 мин     1 мин 30 с      2 мин

 

           Каждый акционер может помочь своему банку: за дополнительный правильный ответ капитал банка увеличивается на 50 р.

Победителем считается тот банк, у которого больше "денег".

           Опыт проведения деловой игры показал, что в её процессе происходит более интенсивный обмен идеями, информацией, она побуждает участников к творческому процессу.

          Пробуждает интерес к отдельно изучаемым темам и математике в целом также использование игры на определенном этапе урока (начало, середина, конец; знакомства с новым материалом, повторение и систематизация изученного).

Так, например, после знакомства с  показательной или логарифмической функцией провожу игру «Назови формулу». Один из учащихся выходит к доске и берет у преподавателя карточку, на которой записана формула некоторой показательной (логарифмической) функции. На доске начерчена таблица.

Один из студентов называет любое значение х. Студент у доски записывает его в таблицу и, подставив это значение в формулу, записывают соответствующее значение у. Ему называют еще одно значение аргумента, он записывает его в следующую клетку и внизу пишет соответствующее значение функции. Ему могут задать еще несколько значений х. Выигрывает студент, который первый назовет формулу, записанную на карточке.

          Большой популярностью среди студентов пользуется игра «Математическое лото». Игра проходит в парах. Перед игрой студенты получают по одной большой карточке, разделенной на определенное число квадратиков с упражнениями, а также то же количество маленьких квадратиков с ответами. Выполняя упражнения, студенты закрывают маленькими квадратиками на большой карточке квадраты с соответствующими примерами. При верных вычислениях после выполнения всех упражнений на карточке окажется, например, портрет великого ученого – математика.

         Не менее любимой для студентов является игра «Математическое домино».

Для этой игры нужно подготовить несколько карточек. Каждую разделить чертой на две половины, на одной стороне записать задание, на другой ответ, но к другому заданию. Одна «начальная» карточка должна иметь задания на обеих половинках. Еще  карточка – только с ответами.

         Итак,  обучающиеся делят карточки между собой, отложив карточку с ответами. Решают примеры на карточках, а, решив, начинают «играть». Начинают игру с карточки, на которой два примера. К ней в обе стороны подставляют ответы, и т.д. Выигрывает тот, кто составили четырехугольник, в виде ромба.

Эта игра проходит с большой пользой, когда задания объединены одной темой.

         За свой многолетний опыт я пришла к выводу, что основным в дидактической игре на уроках математики является обучение математике. Игровые ситуации лишь активизируют деятельность студентов, делают восприятие более активным, творческим, эмоциональным, достойным пониманию. Наибольший эффект игры дают в группах, где студенты с неустойчивым вниманием, пониженным интересом к дисциплине, для которых математика кажется сухой и скучной наукой. Создание же даже незначительных игровых ситуаций на уроках повышает интерес к дисциплине, вносит эмоциональную окраску в учебную работу и разнообразие, а самое главное – снимает утомление и имеет здоровьесберегающую направленность.

              

 

 

 

 

 

 

Литература

1.      Башмаков М.И. Примерная программа общеобразовательной учебной дисциплины «Математика: алгебра и начала математического анализа; геометрия» для профессиональных образовательных организаций. – М.: Издательский центр «Академия», 2015г.

2.      Довгопол И. И., Ивкова Т. А. Современные образовательные и педагогические технологии. – С., мсп «Ната». 2006г.

3.      Игровые технологии на уроках математики / Упоряд. Коць Т. Г. – Тернополь – Харьков, Издательство «Ранок», 2010г.

4.      Интерактивные задания и игры. – Харьков: Издательство Группа «Основа», 2009г.