Отдел образования акимата Кордайского района

Жамбылской области

  Тема:    «Дидактические аспекты развития функциональной              грамотности   учащихся на уроках математики».

Выполнила Абдрахимова Гульнара Сайлауовна                                                        учитель математики  школы-гимназии №1  имени Д.А. Конаева

                                      Кордай-2020г.

Дидактические аспекты развития функциональной грамотности учащихся на уроках математики.

Главой государства Н.Назарбаевым в Послании народу Казахстана от 27 января 2012 года «Социально-экономическая модернизация – главный вектор развития Казахстана» поставлена конкретная задача по принятию пятилетнего Национального плана действий по развитию функциональной грамотности школьников. Данная задача актуализируется в процессе вхождения Казахстана в число 50 наиболее конкурентно-способных стран мира. В условиях решения этой стратегически важной для страны задачи главными функциональными качествами личности являются инициативность, способность творчески мыслить и находить нестандартные решения, умение выбирать профессиональный путь, готовность обучаться в течение всей жизни. Все данные функциональные навыки формируются в условиях школы.

В современном, быстро меняющемся мире, функциональная грамотность становится одним из базовых факторов, способствующих активному участию людей в социальной, культурной, политической и экономической деятельности, а также обучению на протяжении всей жизни. Онако, современные исследования показывают, что педагоги общеобразовательных школ республики дают сильные предметные знания, но не учат применять их в реальных, жизненных ситуациях. Результатом развития функциональной грамотности  является овладение обучающимися системой ключевых компетенций, позволяющих молодым людям эффективно применять усвоенные знания в практической ситуации и успешно использовать в процессе социальной адаптации. Ключевые компетенции- это требование государства к качеству личности выпускника средней школы в виде результатов образования, заявленные в ГОСО и учебных программах.

Что же такое функциональная грамотность учащихся? Это:

 -умение пользоваться математическим языком;

- умение составлять математические модели различных реальных ситуаций;

- умение выбирать наиболее рациональный (оптимальный) способ решения задачи;

- умение сравнивать, анализировать, обосновывать, аргументировано опровергать;

- владение логическим, абстрактным, алгоритмическим, научным мышлением;

- уверенное владение вычислительными навыками.

Этот перечень можно продолжать, но главное состоит в освоении математическим аппаратом, помогающем заниматься в последствии исследовательской деятельностью.

Я хочу остановиться на проектном методе обучения, который входит в жизнь школ как требование времени, своего рода ответ системы образования на социальный заказ государства и родительской общественности..Бытует мнение, что работа над проектами возможна лишь в системе работы с одаренными и высоко мотивированными к учению детьми. Это в корне не верно. В любых классах работа над проектами дает положительные результаты. Проектирование есть универсальное умение, которым должны в той или иной мере овладеть все учащиеся. Внедрять проектное обучение надо в учебно-воспитательный процесс общеобразовательной школы как элемент всеобуча.

Исследовательские работы в школьном курсе математики

Существенную роль в усилении прикладной и практической направленности курса математики и одновременно в развитии способностей учащихся к самостоятельным исследованиям играют задания, выполнение которых представляет собой относительно завершенный исследовательский цикл: наблюдение-гипотеза-проверка гипотезы. В качестве таких заданий целесообразно использовать исследовательские работы. Исследовательские работы удачно вписываются в общую структуру учебного процесса, позволяя связать отдельные вопросы курса алгебры между собой и с курсами геометрии и физики, а также осуществить достаточно серьезную пропедевтику некоторых вопросов из школьного курса начал анализа. Часть исследовательских работ может быть реализована не только на уроке, но и в качестве домашнего задания. В последнем случае на уроке обсуждаются результаты, полученные учащимися дома.

Примеры исследовательских работ, которые я проводила при изучении отдельных тем алгебры.

Понятие функции формируется в 6-7 классах на основе понятия зависимости. Для становления диалектико-материалистического мировоззрения школьников этот этап крайне важен. Мировоззрение формируется путем акцентирования прикладных аспектов обучения, связи математики с жизнью, с другими предметами естественно-математического цикла. Выполняя исследовательские работы, ученики на конкретных, самостоятельно установленных зависимостях усваивают проблематику, которая затем будет являться ядром всей функциональной линии курса математики средней школы.

Первая работа проводится или непосредственно перед изучением темы «Функция» или в начале этой темы.

 Работа №1 Исследование зависимости площади прямоугольника от его длины при постоянном периметре.

Периметр прямоугольника 24 см, а его длина х см. Задайте формулой зависимость площади S (см²) прямоугольника от х. Заполните таблицу

При каком значении  х  у вас получился прямоугольник наибольшей площади? Каково наибольшее из полученных значений S?

Выберите сами два каких-либо допустимых значения  х и вычислите  соответствующие им значения S.

Удалось ли вам получить значение S, большее, чем найденное ранее? Какую гипотезу можно высказать на основании  проведенного исследования о форме прямоугольника наибольшей площади, имеющего данный периметр?         

Работа № 2 Построение графика зависимости высоты столба жидкости в сосуде от объема жидкости. Построение графика

  Приборы и материалы: ведро стандартное (цилиндрической или усеченно- конической формы), банка литровая, линейка.

Указания к работе: 1) налейте в ведро 1 л воды; 2) измерьте высоту столба жидкости в ведре (опустив в ведро линейку), 3) запишите полученный результат в таблицу

 4) повторяйте указанные действия, пока не заполните эту таблицу

Постройте график зависимости h от V (на оси h: 1 см соответствует 2 см высоты стол5а воды, на оси V: 1 см соответствует 1 л воды).Какой график у вас получился: прямолинейный или криволинейный?

В отличие от других работ, которые могут быть как классными, так и домашними, иссле­дование зависимости высоты столба воды в вед­ре от ее объема выполняется только в домашних условиях. На следующем уроке результаты работы обсуждаются. Анализ различий в графиках, полученных школьниками, использовав­шими ведра различной формы, послужит разви­тию физических представлений о равномерных и неравномерных процессах. Работу целесообразно провести при изучении темы «График функции».                                                                                                                                                                                                                                                                        Следующее задание наряду с развитием пред­ставлений о координатной плоскости осу­ществляет пропедевтику темы «Линейное урав­нение с двумя переменными». Его можно пред­ложить непосредственно перед изучением темы. Тогда результаты можно будет использовать для проблемного изложения темы «График линейного уравнения с двумя переменными».

Работа №3 Исследование некоторых простейших множеств точек координатной плоскости.                                                                                                                              Постройте на координатной плоскости несколько точек, у которых сумма абсциссы и ординаты равна 10 (при выборе координат точек используйте и отрицательные числа) В чем особенность расположения построенных точек?                                                                                                                                                Выскажите гипотезу о том, как располагаются на плоскости все точки, у которых суммы координат равны 10. Возьмите несколько точек, у которых сумма абсциссы и ординаты: а) больше 10; б) меньше 10. Выскажите гипотезу о расположении на плоскости точек, сумма координат каждой из которых: а) больше 10; б) меньше 10.

Работа № 4 График расстояния

Постройте на координатной плоскости  прямую  Зх+4у= =12. Производя с помощью измерительного циркуля и линейки необходимые измерения, заполните таблицу

 где х - абсцис­са точки на прямой Зх+4у= 12,  d - расстояние от этой точки до начала координат.Постройте график зависимости d от х.

   При обсуждении результатов полезно пред­ложить учащимся высказать предположения о поведении графика функции d вне рассмотрен­ного промежутка. Работа может быть проведе­на как в процессе изучения темы «График ли­нейного уравнения», так и при обобщающем повторении в конце года.

    Следующая  работа имеет одной из целей формиро­вание отчетливых представлений о различии между понятиями расстояния от некоторой точ­ки и пройденного пути. Следует отметить, что авторы многих учебников смеши­вают эти понятия. Так, в некоторых задачах они предлагают по одному графику ответить на вопросы о скорости движения  на каком-то промежутке и о расстоянии от начального пунк­та в данный момент времени. В других зада­чах авторы полагают возможным по наличию у графика (зависимости расстояния от време­ни) горизонтальной части  сделать вы­вод о неподвижности объекта. Работа №5 можетбыть предложена учащимся при изучении темы «График функции», или на следующих этапах обучения с целью повторения и закрепления соответствующего материала.

Работа № 5 .График расстояния

Туристы отправились на байдарках по течению реки из пункта А в пункт В со скоростью 5 км/ч. После 3 ч пути они сделали остановку на 1ч, а затем поплыли дальше со скоростью 6 км/ч. На рисунке изображена схема маршрута туристов, на которой отмечены отрезки пути длиной в 1 км.

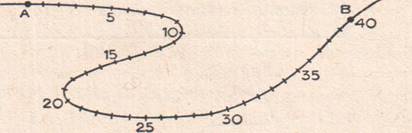
Приборы и материалы: схема маршрута туристов в масш­табе 1 :200000. измерительный циркуль, линейка.

Указания к работе: 1) определите на схеме точку, в ко­торой находились туристы через 1 '1 после отправления из А; 2) найдите расстояние (по прямой) от этой точки до пункта А; до пункта В; 3) запишите полученный ре­зультат в таблицу

 4) выполните указанные действия, вы­бирая приведенные в таблицс значения  t; 5) постройте график зависимости d от t.

Таким образом, данное исследование показало, что школьный курс математики имеет очень большие возможности для анализа различных экономических ситуаций и математи-ческого моделирования различных процессов, протекающих в природе и обществе.                                                                                                                 Проектирование- это деятельность, научить которой может только тот, кто ею владеет. Наибольшие  затруднения вызывает проблематизация – вычленение и формулирование проблемы из целого ряда проблем, формулирование цели проекта. Если учитель владеет проблемным методом, практикует эвристические беседы, проблемное введение в тему и прочее, ему легче освоить проектное обучение. А это, я считаю, один из путей ведущих к развитию функциональной грамотности учащихся на уроках математики.                                            ГОСО предъявляет определенные требования к содержанию учебной деятельности на уроке и необходимым компетенциям учителя.

Поэтому материал урока должен «создавать повод» для организации такой деятельности и постановки учебных заданий, формирующих компетентности функциональной грамотности.