Дидактические материалы по теме «Методы вычисления неопределенного интеграла».

Дидактические материалы по теме «Методы вычисления неопределенного интеграла».

Непосредственное  интегрирование, замена переменных, внесение под знак дифференциала.  Интегрирование по частям.

Краткие теоретические сведения.

1. рал. Таблица интегралов

            Функция F(x) называется первообразной для функции f(x) на интервале (a, b), если для всех x из этого интервала выполняется равенство 

^{F(x)  f (x)}.                                                    (1)

            Неопределенным интегралом от функции f(x) называется множество всех первообразных этой функции, то есть неопределенный интеграл – это выражение вида

 f (x)dx ^ F(x) ^C _{, где} ^{F(x)  f (x)}. Процедуру нахождения неопределенного интеграла называют интегрированием.

2.Свойства неопределенного интеграла. Интегрирование методом подведения под знак дифференциала части подынтегральной функции

 При интегрировании функций наиболее часто используются следующие его свойства:

1) ( f₁(x)  f₂(x))dx ( f₁(x)  f₂(x))dx ;                            2) k  f (x)dx  k ^ f (x)dx ;

                                      3) dz zc .

(cos x3ctgx5)dx

Пример 1.  Найти                                         _.

Решение. Воспользуемся свойствами 1-3, а также таблицей интегралов:

(cos x 3ctgx 5)dx cos x dx ctgx dx⁵^dx ₌ sinx3lnsinx 5xC _.

                                                    _{=                 +3}

sinx3lnsinx 5xC

Ответ: .

Иногда при интегрировании удобно использовать свойство дифференциала: 

1

dx d(axb)

^a                         .                                            (2) dx

Пример 2.  Найти   (3x5)2/3 .

Решение. Согласно формуле (2) можно записать:

1 d(3x5)

dx d(3x5)

            13                (3x5)2/3  (33x5)2/3 .

Теперь воспользуемся свойством 2, а также таблицей интегралов:

 (3xdx5)2/3  13 (3x5)2/3d(3x5)  13 (3x25/)32/131 C13 (3x1/53)1/3 C (3x5)1/3 C.

Ответ: (3x5)1/3 C .

            Инвариантность формул интегрирования позволяет применять при интегрировании  подведение под знак дифференциала части подынтегральной  функции, основанное на следующей формуле: 

 f ((x))(x)dx   f ((x))d(x) .                                       (3)

cos x e^sinx dx

Пример 3.  Найти                            .

Решение. Воспользуемся методом  подведения под знак дифференциала, а также таблицей интегралов:

cos x esinx dx  esinx (sinx)dx =  esinxd(sin x)  esinx  C . =

e^{sin x}

Ответ:            ^C .

3.Интегрирование по частям

Формулой интегрирования по частям называют следующую формулу:

udvuvvdu.                                             (4)

Обычно за ^dv выбирают такое выражение, интегрирование которого не вызывало бы трудностей, а за u – функцию, дифференцирование которой приводит к ее упрощению.  Можно выделить два основных класса интегралов, берущихся по частям: 

       P_n(x) sinbxdx        P_n(x) cosbx dx        P_n(x) e^bxdx        P_n(x) a^bx dx

1)                               ;                                    ;                               ;                                

–  здесь за  u принимают многочлен ^Pn(x),за ^dv – оставшееся выражение, тоесть, напримерsinbx ^dx .

     P_n(x) arcsin bx dx      P_n(x) arctgbx dx     P_n(x) lnbx dx

2)                                   ;                                      ;                                 

– здесь за  u принимают обратную функцию, например, arcsinbx,за ^dv – оставшееся выражение,тоесть P_n(x)dx .

Образцы:  

 x1519x¹⁸6 dx  1915 x1919x¹⁸6 dx  1915  (x¹⁹x196)6dx 1915d(xx19¹⁹66)  1915 ln x₁₉  6 _C .

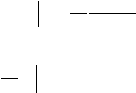
Проверим результат дифференцированием:  1915 ln x19  6   1915 191 6 (19 x18)  x1519x186 ,



x 

следовательно, выполнено условие (1).

15 19 6C ln x 

Ответ: ¹⁹.

(13x1)ln(14x)dx

б) Интеграл  относится к типу интегралов, берущихся по частям; это интеграл так называемого второго типа. Используя формулу (4), получим:

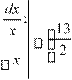
1

                                                     u  ln(14x); du  14 

 (13x 1)ln(14x) dx  dv  (13x 1)dx;  v¹⁴^x13 ₂               x²  x_^ ln(14x)  _^¹³2 x²  x^_ ^dxx   x

2

 (6,5x²  x)ln(14x) (6,5x 1)dx (6,5x²  x)ln(14x) 3,25x²  x C _.

Проверим результат дифференцированием:

  (13x1)ln(14x)  (6,5x² x)14  6,5x1 (6,5x2  x)ln(14x) 3,25x2  x  14x

 (13x1)ln(14x)6,5x16,5x1 (13x1)ln(14x)_. (6,5x² x)ln(14x)3,25x² xC .

Ответ:

Контрольные вопросы.

1.     Первообразная и неопределенный интеграл.

2.     Табличные интегралы.

3.     Свойства неопределенного интеграла. 4. Вывод формулы для интегрирования по частям.

Примеры для самостоятельного решения:

Задача 1.Найти неопределенные интегралы:

,  a)(nxn4)4 xn123 x12dx , b) (n6)xn3   c) cossinnxxdx

                                                      xn 4  6    dx

d) ((n 1)x 1)ln(2nx dx) ,    e) ln xdx ,  f ) _e^x sin xdx

В примерах a), b), c) правильность полученных результатов проверить дифференцированием.