-  1 -

Дидактические материалы по теме «Приближенное вычисление определенных интегралов»

Требуется научиться   вычислять  определенные интегралы  по формулам прямоугольников, трапеций и Симпсона и находить погрешность полученных значений интеграла методом двойного пересчета.

Краткие теоретические сведения.

Постановка задачи численного интегрирования

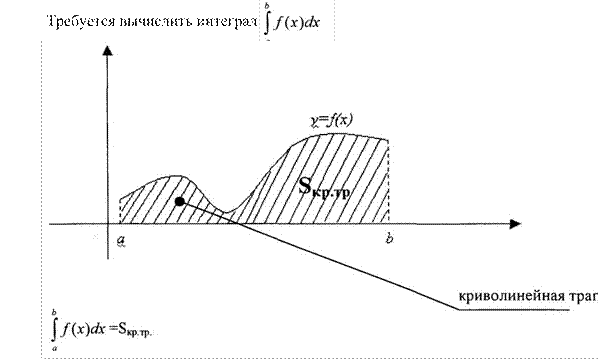
Задача численного интегрирования - заменить криволинейную трапецию простой геометрической фигурой: прямоугольником, трапецией и др.

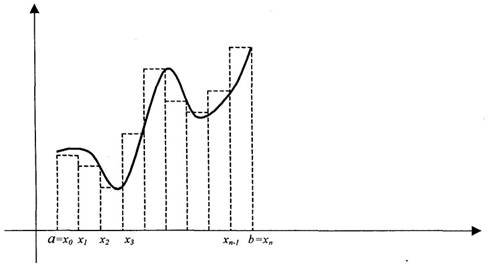
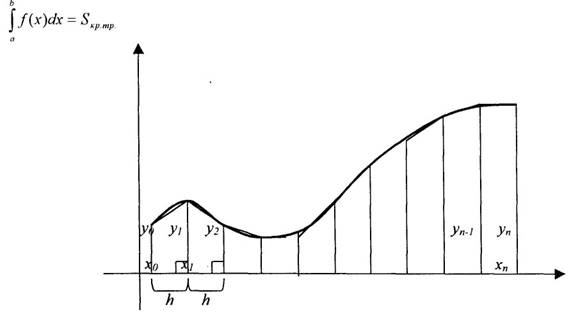
Формула прямоугольников

Левосторонняя формула прямоугольников:

-  2 -

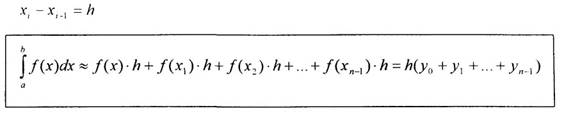
Расстояние между соседними значениями х обозначается Н и называется шагом

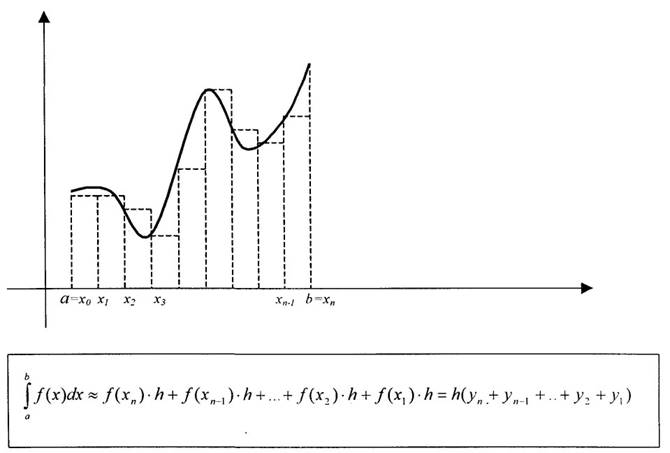
Правосторонняя формула прямоугольников:

Пример:

Вычислить интеграл

1)      точно

2)      по формуле левых прямоугольников

3)      по формуле правых прямоугольников

Решение.

-  3 -

2)

= 0,1 • (0,00001 + 0,00032 + 0,00243 + 0,01024 + 0,03125 + 0,07776 +

+ 0,16807 + 0,32768 + 0,59049) = 0,120834

3)

= 0,1(0,00032 + 0,00243 + 0,01024 + 0,3125 + 0,07776 + 0,16807 + 0,32768 +  +0,59049+1)=0620824

Среднее арифметическое:

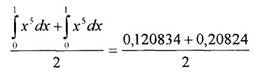= 0,164537*0,16

Формула трапеций.

-  4 -

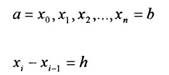
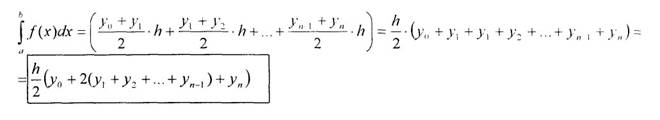
Пример:

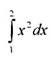= 0,05 • (1 + 2(1,21 +1,44 +1,69 +1,96 + 2,25 + 2,56 + 2,89 + 3,24 + 3,61) + 4) = 2,34

= 2,34-2,33 =0,01

Формула Симпсона.

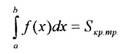
Разбиваем на 2п частей. 

Погрешность формул численного интегрирования

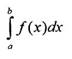
Для формулы прямоугольников:

Для формулы трапеций:

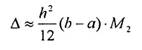
Для формулы Симпсона:

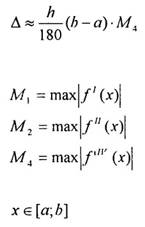
Поскольку нахождение производных не всегда просто, то на практике используется метод двойного пересчёта, т.е. при вычисление интеграла с шагом I  получается значение

Если

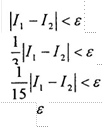
-  для формулы прямоугольников;

-  для формулы трапеций;

-  для формулы Симпсона,

-  погрешность, за значение интеграла берётся

где

Если эти равенства не выполняются, то берём шаг и вычисляем

Пример:  Вычислим интеграл, используя формулу прямоугольников.  Пусть требуется определить значение интеграла функции на отрезке   . Этот отрезок

  на     травных отрезков длиной 

  значение функции  в точках

    Формулы выражают площадь ступенчатой фигуры,

составленной из  прямоугольников:

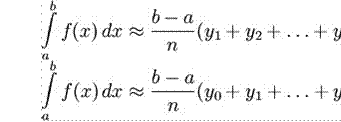
1

Данная подинтегральная функция f x  2 ^x2 . Отрезок 0;4  разобьем на 5 отрезков с

h  4^50  0,8. Зададим функцию  f x _ 2^1x₂ таблицей: Шагом равным

^0 ^{2 x2}          0,8(0,05+0,08+0,13+0,22+0,38)=0,69 4

1

 ^{2 x2dx }0,8(0,08+0,13+0,22+0,38+0,5)= 1.048

⁰

 0,87

Среднее значение интеграла равно 

Вычислим тот же интеграл, используя формулу  трапеций.

Полная формула трапеций в случае деления всего промежутка интегрирования на отрезки одинаковой длины h:

.

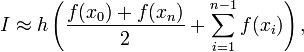
Используем ту же таблицу. 4

1

0 ^{2 x2dx }0,50,8(0,5+2(0,38+0,22+0,13+0,08)+0,05)= 0,87 Вычислим тот же интеграл, используя формулу  Симпсона.

Формулой Симпсона называется интеграл от интерполяционного многочлена второй степени на отрезке [a,b]:

b

h

    ^ f x  ₃y₀ 4(y₁   y₃                    ...         y_n1)2(y₂  ... y_n2 y_n⁾

_a

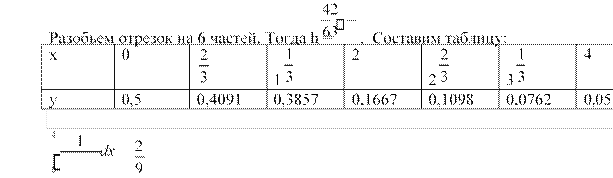^2x2         = (0,5+4(0,4091+0,1667+0,0762)+2^{0,3857+0,1098}+0,05)= 0,922

Для сравнения найдем точное значение интеграла: 

4

               1              1              x     ₄

       ^ _{2 x}2dx  ₂ arctg    ₂    0  0,87

0  

2).Контрольные вопросы:

1.    Формулы правых и левых прямоугольников.

2.    Формула трапеций.

3.    Формула Симпсона.

4.    Метод двойного пересчета для нахождения погрешности по формулам прямоугольников, трапеций и Симпсона.

5.    Метод «двойного пересчета».

3) Задания для самостоятельного решения.   (n – номер варианта) 1.Вычислить интеграл   

2 nx2 1

0 ^{x n} dx, 

используя формулы  левых и правых прямоугольников, трапеций и Симпсона с числом шагов 4 и 8. Оценить погрешность вычислений методом двойного пересчета.  Для сравнения найти точное значение интеграла. 

2. 1.Вычислить интеграл   

1

(e^x2 nxdx) , 

0

используя формулы  левых и правых прямоугольников, трапеций и Симпсона с числом шагов 4 и 8. Оценить погрешность вычислений методом двойного пересчета.