
Министерство науки и высшего образования РФ
Федеральное бюджетное государственное образовательное учреждение
высшего образования
«Забайкальский государственный университет»
Психолого-педагогический факультет
Кафедра теории и методики дошкольного и начального образования
Выпускная квалификационная работа
ФОРМИРОВАНИЕ У МЛАДШИХ ШКОЛЬНИКОВ УЧЕБНЫХ ДЕЙСТВИЙ ЦЕЛЕПОЛАГАНИЯ, ПЛАНИРОВАНИЯ И ПРОГНОЗИРОВАНИЯ ПРИ РЕШЕНИИ АРИФМЕТИЧЕСКИХ ЗАДАЧ
44.03.01 Педагогическое образование
Профиль «Начальное образование»
|
|
Выполнила: студентка 4курса Группа НОс-17 Васильева Ольга Ивановна
Научный руководитель: Клименко Татьяна Константиновна профессор, доктор педагогических наук
|
Допущена к защите кафедрой
Теории и методики дошкольного и
начального образования
Зав.кафедрой_________ А.И. Улзытуева
«___»______________2021г.
Чита, 2021
СОДЕРЖАНИЕ
|
Введение……………………………………………………………………………………… |
3 |
|
Глава I. Теоретические предпосылки проблемы формирования у младших школьников учебных действий целеполагания, планирования и прогнозирования при решении арифметических задач ……………………………………………………………………… |
8 |
|
1.1. Психолого-педагогические особенности детей младшего школьного возраста……………………………………………………………………………………….. |
8 |
|
1.2. Проблема формирования учебных действий целеполагания, планирования и прогнозирования в современной теории и практике начального образования………………………………………………………………………………….. |
14 |
|
1.3. Понятие текстовые задачи………………………………………………………….. |
21 |
|
1.4. Способы формирования у младших школьников учебных действий целеполагания, планирования и прогнозирования при решении арифметических задач…………………………………………………………………………………………. |
28 |
|
Вывод по первой главе……………………………………………………………………... |
34 |
|
Глава II. Опытно-экспериментальная работа по формированию у младших школьников учебных действий целеполагания, планирования и прогнозирования при решении арифметических задач…………………………………………………………… |
35 |
|
2.1. Диагностика уровня сформированности у младших школьников учебных действий целеполагания, планирования и прогнозирования ………………………….. |
35 |
|
2.2. Задания, направленные на формирование у младших школьников учебных действий целеполагания, планирования и прогнозирования при решении арифметических задач……………………………………………………………………… |
43 |
|
2.3. Анализ результатов опытно-экспериментальной работы …………....................... |
51 |
|
Вывод по второй главе……………………………………………………………………… |
57 |
|
Заключение………………………………………………………………………………….. |
58 |
|
Список использованных источников………………………………………………………. |
61 |
|
Приложения…………………………………………………………………........................ |
65 |
Введение
Актуальность исследования. В Российской Федерации за последние годы произошло много изменений, а именно изменения в системе научных знаний, усложнение содержания учебного материала школьного образования с отсутствием необходимой заинтересованности и внимания к проблеме развития учебного процесса. Все эти изменения приводят к несформированности у обучающихся умения учиться.
Перед современной школой встал и остается важным вопрос эффективного и самостоятельного усвоения обучающимися новых знаний, умений и компетенций, в том числе и умение, учиться. Возможности для решения данного вопроса даёт освоение универсальных учебных действий у обучающихся.
По этой причине в Федеральном Государственном Образовательном Стандарте второго поколения прописаны не только предметные, но и метапредметные и личностные результаты
Главной целью образования в школе является формирование у обучающихся возможности самостоятельно выявлять учебные цели, планировать методы достижения данных целей и прогнозировать результат, контролировать и производить оценку результатов своих действий.
Одно из средств формирования универсальных учебных действий - решение арифметических задач. Опрос учителей начальных классов показал, что обучающиеся достаточно часто испытывают затруднения при решении арифметических задач. Затруднением могут быть связанны с отсутствием (или слабым владением) умение анализировать текст задачи. Так же, при решении арифметических задач, учителя чаще всего прибегают к традиционному методу решения арифметических задач (обычная краткая запись). Причиной этой проблемы является недостаточная оснащенность учителей начальных классов методическими разработками по работе с арифметическими задачами в рамках ФГОС.
Представление «регулятивные универсальные учебные действия» возникло недавно. В течении последних десяти лет многочисленными учеными рассматривается вопрос развития самоорганизации у обучающихся. Тем не менее, вопрос поиска средств развития умений к самоорганизации у учащихся затрагивает и по сей день, а внедрение новейшего термина «регулятивные универсальные учебные действия» в Федеральный государственный образовательный стандарт начального общего образования только доказывает его актуальность.
По мнению авторов концепции формирования универсальных учебных действий (А.Г. Асмолов, Н. Ф. Талызина, Д. Б. Эльконин В. В. Давыдов и др.), регулятивные универсальные учебные действия обеспечивают организацию учебной деятельности обучающегося. К ним относятся целеполагание, планирование, прогнозирование, контроль, оценка, коррекция, саморегуляция.
Формирование универсальных учебных действий на уроках математики в начальной школе изучали и изучают до сих пор. Сущность универсальных учебных действий раскрыта в трудах следующих авторов: М. А. Бантова, Н. Б. Истомина, А. В. Белошистая, Г. В. Бельтюкова, М. И. Моро.
При изучении психолого – педагогической литературы нами было выявлено противоречие между большим количеством материалов о формировании регулятивных УУД на уроках в начальной школе и небольшим количеством информации о формировании у младших школьников учебных действий целеполагания, планирования и прогнозирования при решении арифметических задач.
Проблема заключается в необходимости более подробно исследовать формирование у младших школьников учебных действий целеполагания, планирования и прогнозирования при решении арифметических задач
Эта проблема дала возможность сформулировать тему исследования: «Формирование у младших школьников учебных действий целеполагания, планирования и прогнозирования при решении арифметических задач».
Объект исследования – процесс решения арифметических задач в начальных классах.
Предмет исследования – возможности формирования у младших школьников учебных действий целеполагания, планирования и прогнозирования при решении арифметических задач во 2 классе.
Цель исследования – исследование особенностей формирования у младших школьников учебных действий целеполагания, планирования и прогнозирования при решении арифметических задач.
Задачи исследования:
1) изучить психолого-педагогическую и методическую литературу по проблеме исследования;
2) изучить пути решения проблемы формирования действий целеполагания, планирования и прогнозирования в современной теории и практике начального образования;
3) выявить основные характеристики текстовых задач;
4) определить способы формирования у младших школьников учебных действий целеполагания, планирования и прогнозирования при решении арифметических задач
5) подобрать диагностический инструментарий и выявить уровни сформированности учебных действий целеполагания, планирования и прогнозирования у младших школьников;
6) на основе анализа теоретической и научно-методической литературы подобрать методы и приемы, направленные на формирование формированию у младших школьников учебных действий целеполагания, планирования и прогнозирования при решении арифметических задач;
7) провести анализ опытно – экспериментальной работы.
Гипотеза исследования: Мы предположили, что для успешного формирования у младших школьников учебных действий целеполагания, планирования и прогнозирования необходимо использовать специально разработанный комплекс заданий, способствующий у младших школьников формированию учебных действий целеполагания, планирования и прогнозирования при решении арифметических задач.
Проблема, цель и гипотеза исследования обусловили решение следующих задач:
Для решения поставленных в исследовании задач были использованы следующие методы: анализ психолого-педагогической и методической литературы по теме исследования; наблюдение за деятельностью обучающихся; беседа с учителями и обучающимися; опытно-экспериментальная работа; качественный анализ её результатов.
Научная новизна исследования: заключается в том, что в работе описано, как формировались у младших школьников учебные действия целеполагания, планирования и прогнозирования при решении арифметических задач применительно к МОУ «Горекинская основная общеобразовательная работа».
Теоретическая значимость заключается в рассмотрении теоретического аспекта формирования регулятивных УУД целеполагания, планирования и прогнозирования у младших школьников в процессе решения арифметических задач.
Практическая значимость: заключается в том, что теоретический материал может быть использован учителями начальных классов для самообразования и для подготовки к выступлениям на методических объединениях. Разработанные задания могут быть использованы в практическом обучении младших школьников.
Опытная база исследования: МОУ «Горекинская ООШ», 2 класс, 10 обучающихся.
Структура исследования. Работа состоит из введения‚ двух глав‚ заключения‚ списка использованной литературы и приложения.
Во введении обоснована актуальность темы, сформулированы проблема, цель, объект, предмет и задачи исследования, выдвинута гипотеза, охарактеризованы методы и этапы исследования.
Список использованной литературы насчитывает 34 наименования. В приложении содержатся материалы опытно-экспериментальной работы. Общий объем выпускной квалификационной работы составляет 87 страниц.
Глава I. ТЕОРЕТИЧЕСКИЕ ПРЕДПОСЫЛКИ ПРОБЛЕМЫ ФОРМИРОВАНИЯ У МЛАДШИХ ШКОЛЬНИКОВ УЧЕБНЫХ ДЕЙСТВИЙ ЦЕЛЕПОЛАГАНИЯ, ПЛАНИРОВАНИЯ И ПРОГНОЗИРОВАНИЯ ПРИ РЕШЕНИИ АРИФМЕТИЧЕСКИХ ЗАДАЧ
1.1. Психолого-педагогические особенности детей младшего школьного возраста
Младший школьный возраст – это период развития от 7 до 11 лет, Он знаменуется окончанием дошкольного возраста кризисом 7 лет и началом подросткового возраста в период 11 лет.
В младшем школьном возрасте активно развивается мотивационная сфера.
В период младшего школьного возраста развиваются такие качества как:
нравственность;
эстетика;
этика;
основы поведения;
культура поведения.
В данный период обучающийся постигает процесс учения, ему интересно все новое, но это не касается только учебной деятельности.
Правильное формирование всех вышеперечисленных характеристик именно в младшем школьном возрасте позволит в период подросткового возраста не потерять потребность в удовлетворении познавательной активности.
Во время учебной деятельности проявляется познавательная активность. Интерес у обучающегося к учебной деятельности более активен, когда он успешен в ней [2].
Основные новообразования младшего школьного возраста в познавательной сфере это:[3]:
1) качественно новый уровень развития произвольной регуляции поведения и деятельности;
2) рефлексия;
3) внутренний план действий;
4) развитие познавательного отношения к действительности.
Окончание младшего школьного возраста можно ознаменовать кризисом отрочества, который содержит в себе позиции, когда мотивация учебы исчерпана это еще одна житейская потребность, а содержательный мотив учения не проявился.
Кризис отрочества проявляется в:
невыполнение домашних и занятий в классе, нежелании их выполнять;
нарастающем уровне конфликтности со стороны ученика по отношению к учителям [4].
При переходе в среднюю школу происходит процесс обострения всех знаний, навыков, умений, а неразвитость данных положений усугубляет всю ситуацию [3].
В процессе пристройки ребенок «ориентируется на себя», на свои проявления качеств и умений.
Дошкольное детство заканчивается, когда обучающийся поступает в школу и становится стартовой площадкой младшего школьного возраста (6 — 7 — 10— 11 лет). Младший школьный возраст очень ответственный период школьного детства, от которого зависит уровень интеллекта и личности, желание и умение учиться, уверенность в своих силах[5].
Социальная ситуация развития осуществляется в выходе обучающегося за рамки семьи, в расширении круга значимых лиц.
Согласно концепции Э. Эриксона, в возрасте от 6 до 12 лет начинается приобщение обучающегося к трудовой жизни общества, вырабатывается трудолюбие. Хорошее окончание этой стадии приносит обучающемуся ощущение собственной компетентности и способность действовать наравне с другими людьми; неблагоприятный результат стадии — комплекс неполноценности. На взаимоотношениях с родителями, взрослыми и одноклассниками сказывается его успешность или неуспешность обучения. Психологическая проблема школьного обучения является очень значимой и важной. Современная школа требует высокой развитости функциональной подготовленности от ребенка.
Психологическая готовность есть многоуровневое образование.
Компоненты, входящие в психологическую готовность:
1. Личностная готовность.
- Процесс развития мотивационной сферы, а также его уровень. Познавательные интересы. Желание и цель занять свое место в социальных отношениях, выполнять важную деятельность учения.
- Показателем выступает внутреннее состояние готовности стать школьником [5].
- Произвольная сфера: внимание, памяти, способность выполнять задания по образцу, по намерению.
2. Интеллектуальная готовность.
- Ориентировка в окружающем, запас знаний.
- Уровень развития
восприятия и наглядно - образного мышления. Уровень обобщения умение обобщать и
дифференцировать предметы и ![]() явления.
явления.
- Развитие речевой сферы (в том числе фонематического слуха)[3].
З. Двигательная готовность.
- Мелкая моторика.
- Крупные движения (рук, ног, всего тела).
4. Уровень развития предпосылок учебной деятельности:
- Способность слушать внимательно, выполнять задания
последовательно и по указаниям;
- Самостоятельность при выполнении задания;
- Ориентировка на условия задач как систему, преодолев при этом факторы, которые могут отвлечь.
Нравственность, эстетические положения и основы поведения характеризуют младший школьный возраст. Во время данного периода времени обучающемуся интересно все новое, и не только в процессе обучения – таким образом постигается процесс учения.
В младшем школьном возрасте ребенок выполняет такие же виды деятельности, что и в дошкольном возрасте – игровая деятельность, трудовая, занятия спортом и искусством.
В дошкольном учреждении ведущим видом деятельности была игровая, в младшем школьном возрасте - учебная. Учебная деятельность не рассматривается только в качестве учебных занятий, она рассматривается шире, с позиции получения новых знаний во время труда, отдыха, игры. В это время обучающийся постигает новое и учится. Его знания приобретают все более масштабный характер.
Учебная деятельность
выступает в качестве деятельности, которая непосредственно направленна на
усвоение знаний и умений, выработанных ![]() человечеством
[6].
человечеством
[6].
Становление частью школьного коллектива имеет огромное значение для развития социальных чувств и личности младшего школьника. Обучающийся овладевает нормами и правилами общественного поведения тогда, когда находиться во взаимодействии с одноклассниками и учителями. В данный период времени осваивается навык общения, умения завязывать и поддерживать дружеские взаимоотношения.
Взаимоотношения с одноклассниками изменяются за период обучения в начальной школе. В первом классе восприятие обучающегося опосредовано отношением к нему учителя и уровнем успеваемости, а выбор друга определяется внешними обстоятельствами (оказался рядом за одной партой, живут поблизости). Постепенно, к 10 —11 годам, приобретают значимость личностные качества учащегося (внимательность, самостоятельность, уверенность в себе, честность), его организаторские способности [5].
Основные новообразования младшего школьника следующие:
1.В младшем школьном возрасте у обучающегося возникает множество позитивных изменений и преобразований. Это сенситивный период для формирования познавательного отношения к миру, навыков учебной деятельности, организованности и саморегуляции.
В процессе школьного обучения качественно изменяются, перестраиваются все сферы развития обучающегося. Начинается эта перестройка с интенсивного развития интеллектуальной сферы. Основное направление развития мышления в школьном возрасте — переход от конкретно-образного к словесно-логическому и рассуждающему мышлению[3].
2. Интеллектуальная
рефлексия (способность к осознанию содержания своих действий и их оснований)
является новообразованием, знаменующим начало развития теоретического мышления
у младших школьников. Теоретическое мышление обнаруживается в ситуации,
требующей не столько применения правила, сколько его открытия, конструирования.
В процессе обучения изменяются и другие познавательные процессы внимание, ![]() восприятие,
память. Огромное требование к вниманию обучающегося предъявляется с первого дня
обучения в школе: он должен направит и удержать внимание на предметах, не
обладающих чертами привлекательности и необычности. 10 – 20 минут обучающийся
может без усталости заниматься одним делом.
восприятие,
память. Огромное требование к вниманию обучающегося предъявляется с первого дня
обучения в школе: он должен направит и удержать внимание на предметах, не
обладающих чертами привлекательности и необычности. 10 – 20 минут обучающийся
может без усталости заниматься одним делом.
3. Восприятие из процесса узнавания, различения, опирающегося на очевидные признаки, становится деятельностью наблюдения. Под руководством учителя обучающийся осуществляет наблюдение. Цель наблюдения – обследовать предмет или явление, ознакомить обучающихся с правилами восприятия и обратить внимание на главные и второстепенные признаки, обучить способам регистрации результатов наблюдений (в виде записей, рисунка, схемы). Восприятие становится синтезирующим и устанавливающим связи, преднамеренным, целенаправленным наблюдением за объектом[4].
4. Память развивается в
двух направлениях произвольности и осмысленности. Обучающийся непроизвольно
запоминает интересный материал, который доступно изложен в игровой форме и т.д.
Так же обучающийся может запоминать материал, который им не интересен. С каждым
годом обучение строиться с опорой на произвольную память [15]![]()
5. Младшие школьники так же, как и дошкольники, обладают хорошей механической памятью. За время обучения в начальной школе обучающиеся механически заучивают тексты. Но в старших классах при механическом заучивании обучающиеся испытываю трудности, потому, что тексты становятся больше по объему и сложнее по содержанию. Совершенствование смысловой памяти в этом возрасте даст возможность освоить достаточно широкий круг мнемонических приемов, т.е. рациональных способов запоминания (деление текста на части, составление плана, приемы рационального заучивания и т.д.).
Деятельность младшего школьника целенаправленно на постижение окружающего мира, его восприятие, создание целенаправленных занятий, которые смогут развить чувственное восприятие. Посредством развивающих занятий можно развить чувственное восприятие окружающего мира.
Развитие творческих способностей является важным этапом в становлении и развитии личности.
Младший школьник через познание окружающего мира становится более социализированным и адаптированным к быстро меняющимся жизненным условиям.
Таким образом, в период младшего школьного возраста ведущей деятельностью становится учение. Учебная деятельность выступает в качестве деятельности, которая непосредственно направлена на усвоение знаний и умений, выработанных человечеством. Ведущая деятельность способствует развитию рефлексии и познавательных процессов.
1.2. Проблема формирования учебных действий целеполагания, планирования и прогнозирования в современной теории и практике начального образования
Проблема формирования регулятивных универсальных учебных действий актуальна в младшем школьном возрасте, так как для младшего школьного возраста характерно формирование учебной деятельности, развитие которой происходит через усвоение человеческого опыта, представленного в форме научных знаний.
Возможность для развития психических процессов и построения внутреннего плана действий младший школьник получает в процессе учебной деятельности. Эти новообразования младшего школьного возраста входят в состав основных компонентов регулятивных универсальных учебных действий, поэтому формирование регулятивные универсальные учебные действия становится приоритетной задачей младшего школьного возраста.
Особенности младшего школьного возраста наиболее подробно описаны В.В. Давыдовым, Д.Б. Элькониным и их коллегами А.К. Дусавицким, А.К. Марковой и другими. Границы младшего школьного возраста совпадают с периодом обучения в начальной школе, устанавливаются в настоящее время с 6-7 до 9-10 лет [6].
При изучении учебной деятельности младшего школьника В.В.Давыдов и Д.Б. Эльконин выделили следующие её компоненты:
• учебно-познавательные мотивы;
• учебные задачи;
• учебные операции или действия;
• контроль и самооценка.
Все эти компоненты отражены в Федеральном государственном образовательном стандарте начального общего образования [29]. ФГОС НОО ориентирован на достижение личностных, предметных и метапредметных результатов. Метапредметные результаты включают в себя формирование универсальных способов учебной деятельности, которые обеспечивают их успешность в познавательной деятельности на всех этапах дальнейшего образования.
Универсальные учебные действия – это система учебных действий учащегося, позволяющая самостоятельно осваивать новые знания об окружающем мире, а также успешно организовывать процесс познания с целью повышения качества своего образования. Формирование универсальных учебных действий требует более глубокого изучения. А.Г. Асмолов в своих работах пишет, что универсальные учебные действия в процессе обучения в начальной школе выполняют четыре важные функции. «Первая функция – обеспечение возможности обучающегося самостоятельно осуществлять учебную деятельность. Вторая – обеспечение правильной постановки учебной цели в рамках учебной деятельности. Немаловажной функцией является поиск и использование необходимых средств и способов достижения учебных целей. Третья функция – это контроль и оценка учебного процесса, а также результаты учебной деятельности. Создание благоприятных условий для гармоничного развития личности и её самореализации на основе готовности к непрерывному образованию тоже относится к функциям универсальных учебных действий. Четвертая функция, обеспечивающая успешное усвоение новых знаний и формирование умения, навыков и компетентности в любой предметной области» [6, с. 65]. Важное место в формировании умения учиться у младших школьников занимают именно регулятивные универсальные учебные действия, так как они обеспечивают организацию, регуляцию и коррекцию учебной деятельности. Усвоение знаний, умений и навыков в учебной деятельности выступает как цель и главный результат деятельности. Учебная деятельность осуществляется в весь период обучения в школе, она является ведущей только тогда, когда она складывается и формируется,.
«Согласно Федеральному государственному образовательному стандарту начального общего образования к регулятивным универсальным учебным действиям относятся: целеполагание, планирование, прогнозирование, контроль, коррекция, оценка и саморегуляция» [29, с. 47].
1) Регулятивные УУД:
1. Целеполагание как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимися, и того, что еще неизвестно.
2. Планирование - определение последовательности промежуточных целей с учетом конечного результата, составление плана и последовательности действий.
3. Прогнозирование - предвосхищение результата и уровня усвоения знаний, его временных характеристик.
4. Контроль - сличение способа действий и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона.
5. Коррекция - внесение необходимых дополнений и корректив в план, и способ действия.
6. Оценка - осознание уровня и качества усвоения.
7. Саморегуляция как способность к мобилизации сил и энергии, к волевому усилию и к преодолению препятствий [2, 9].
Рассмотрим более подробно учебные действия целеполагания, планирования и прогнозирования.
Перейдём к анализу компонентов регулятивных универсальных учебных действий младших школьников. Первым компонентом к изучению является целеполагание. Целеполагание – это процесс формирования и выдвижения целей. Исследованием действия целеполагания у младших школьников занимались такие известные учёные как Л.И. Божович, В.К. Котырло, Л.С. Лучанская, З.В. Мануйленко, С.Н. Рубцова. Они рассматривали специфику осуществления целенаправленных действий, самостоятельной постановки целей, сознательного подчинения правилам и оценки своих действия. Также изучением действия целеполагания у обучающихся младшего школьного возраста занималась авторская группа разработчиков ФГОС НОО А.Г. Асмолов, Г.В. Бурменская, И.А. Володарская, О.А. Карабанова, Н.Г. Салмина, С.В. Молчанов. Анализируя развитие целеполагания в начальной школе, учёные выделили шесть уровней:
• Первый уровень – принятие простейших целей, которые не предполагают выполнение промежуточной цели;
• Второй уровень – принятие и выполнение только практических задачи, а в теоретических задачах не ориентируется;
• Третий уровень – переопределение познавательной задачи в практическую, где обучающийся принимает и выполняет только практические задачи в теоретических задачах не ориентируется;
• Четвертый уровень – принятие познавательную цель и сохранение при выполнении учебных действий и регуляция всего процесса выполнения, а также четкое выполнения требований познавательной задачи;
• Пятый уровень – столкновение с новой практической задачей, формулировка познавательной цели и построение действий в соответствии с ней;
• Шестой уровень – самостоятельная формулировка познавательной цели обучающимся, выходящая за пределы требований программы. Целеполагание является одним из важных компонентов регулятивных универсальных учебных действий, у обучающихся он обычно находится на среднем уровне, где школьники хорошо ориентируются в практических задачах, но с трудом выполняют теоретические.
Целеполагание как осмысление предложенной цели важно для организации учебной деятельности. При этом отметим, что цель урока, которую ставит перед собой учитель, и цель урока, сообщаемая детям, созвучны, но не одинаковы. Цель урока для учителя – есть проекция образовательного результата, и она отличается более развёрнутой формулировкой. Когда дети научатся читать, они могут прочитать цель урока, написанную на доске и объяснить её своими словами. Не менее важным моментом целеполагания наряду с пониманием цели является её принятие, то есть видение актуальности цели для конкретной личности.
Чтобы обучающиеся научились формулировать цель урока нужно ответить на вопросы: «Зачем?» и «Для чего и где можно использовать полученные знания?».
Перечислим приёмы организации принятия цели, выделенные З. А. Кокаревой:
– опора на личный жизненный опыт обучающихся;
– использование занимательного игрового материала;
– создание проблемной ситуации в процессе целеполагания;
– выбор цели из предложенных учителем формулировок, обоснование выбора цели;
– моделирование цели урока, введение понятия «учебная задача»;
– постановка цели в том числе и на длительный период времени с помощью карты знаний, маршрута движения[17, 58].
Начало обучения в школе тесно связано с формированием умения планировать, поэтому следующий компонент, который мы рассмотрим – это планирование.
Анализируя практику обучения А.З. Зак, А.К. Маркова, Г.Г. Микулина, выявили, что успешность осуществления учебной деятельности во многом зависит от возможностей младших школьников предусмотреть предстоящие действия, от умения выделить различные варианты выполнения задания, проанализировать особенности каждого варианта и выбрать верный.
Все эти действия включает в себя действие планирования. Планирование – это последовательность промежуточных целей с учетом конечного результата, а также составление плана и последовательности действий. Вопросом изучения планирования в младшем школьном возрасте занимались такие учёные как Л.И. Айдарова, В.В. Давыдов, Л.К. Максимов, Д.Б. Эльконин. Учёными было установлено, что у младших школьников наряду с эмпирическим мышлением формируется и теоретическое мышление, именно поэтому изучение предметного содержания процесса планирования, условий его развития целесообразно начать именно в младшем школьном возрасте. Подтверждая вышесказанное Е.И. Исаева, О.В. Клюевой, В.Х. Магкаева, Я.А. Пономарёва, O.K. Тихомирова в своих работах отмечают, что формирование планирующей функции мышления лучше всего осуществляется в младшем школьном возрасте во внеурочной деятельности.
Формирование универсального учебного действия планирования начинается с введения определения понятия «план» – это порядок, последовательность действий [28, 467]; со знакомства с картинным планом сказки, словесным планом произведения, планом (алгоритмом, инструкцией) известных обучающимся действий (заправить кровать, полить цветы, рассказать сказку). Со временем обучающиеся должны научиться составлять план действий по решению учебной задачи.
Обучающиеся в первом классе с трудом читают, поэтому для них уместен графический план урока с использованием условных обозначений из учебника. Во время работы на уроке учитель вместе с обучающимися должен обращаться к плану урока, отмечать выполнение этапов плана и последующие действия, проводить контроль по ходу решения учебной задачи, проводить коррекцию действий и оценивание [34,105].
Охарактеризуем ещё один компонент регулятивных универсальных учебных действий – прогнозирование. Действие прогнозирования также органично включается в систему развития всей познавательной деятельности обучащихся. Среди отечественных ученых изучением проблемой действия прогнозирования занимались Л. В. Занков, Н. Н. Лобанова, В. X. Магкаев, Н. И. Непомнящая, А. И. Раев и другие. А.Г. Асмолов считает, что использование приёмов прогнозирования в начальной школе может помочь в увличении скорости устных вычислений. К сожалению, на изучение и применение действия прогнозирования в работе младшего школьника отводиться не так много времени, что значительно снижает уровень освоения регулятивных универсальных учебных действий.
В толковом словаре Д.Н. Ушакова сказано, что прогноз это предсказание о развитии и исходе каких - нибудь событий, явлений на основании имеющихся данных [28]. Прогнозирование - это предвосхищение результата и уровня усвоения знаний, его временных характеристик.
Во-первых, прогнозирование понимается как «процесс исследования», «анализ», «сторона познавательной деятельности», то есть как познавательная деятельность человека.
Во-вторых, прогнозирование понимается как познавательная деятельность, которая приводит к знанию будущего при определенных условиях.
В-третьих, прогнозирование определяется как познавательная прогностическая деятельность, результат которой имеет специфику: отражение будущего с учетом вероятности его наступления и различной временной перспективы [19, 4].
Формирование учебных действий целеполагания, планирования и прогнозирования является неотъемлемой частью Регулятивных универсальных учебных действий. Именно в младшем школьном возрасте актуальной становится задача формирования регулятивных универсальных учебных действий, так как на данном этапе учебная деятельность является ведущим видом деятельности обучающегося.
1.3. Понятие текстовые задачи
С термином «задача» люди постоянно сталкиваются в повседневной жизни, как на бытовом, так и на профессиональном уровне. Каждому из нас приходится решать те или иные проблемы, которые зачастую мы называем задачами. Это могут быть общегосударственные задачи (освоение космоса, воспитание подрастающего поколения, оборона страны и т.п.), задачи определенных коллективов и групп (сооружение объектов, выпуск литературы, установление связей и зависимостей и др.), а также задачи, которые стоят перед отдельными личностями.
К решению разноплановых жизненных задач обучающихся начинают готовить уже в младшем школьном возрасте в процессе обучения математике.
Решая задачи, обучающиеся приобретают новые или закрепляют, углубляют и систематизируют уже имеющиеся математические знания. Обучающая функция текстовых задач может быть продемонстрирована задачами, в которых раскрывается конкретный смысл арифметических действий, вводятся рациональные приемы вычислений и соответствующие им правила, выполняются табличные или внетабличные вычисления, используются соотношения между различными единицами измерения величин и т.д.
Главной особенностью текстовой задачи то, что в ней не указывается какое именно действие (или действия) нужно выполнить для получения ответа на требование задачи:
Понятие текстовой задачи – очень многоплановое. Именно поэтому единую классификацию видов задач составить невозможно. Классификацию видов текстовых задач сводят к выделению следующих параметров, на основании которых их объединяют в группы:
а) количество действий, которые необходимо выполнить для решения задачи: простые и составные, (арифметические, вычислительные задачи).
б) соответствие числа
данных и искомых (определенные задачи - это задачи, в которой условий столько,
сколько необходимо и достаточно для получения ответа; задачи с альтернативным
условием - это задачи, в ходе решения которых необходимо рассматривать
несколько вариантов, а ответ ![]() находится после того, как
условия будут исследованы; переопределенные задачи имеющие условия, которые не
используются при их решении выбранным способом; неопределенные задачи
недостаток данных в которых не позволит ответить на вопрос задачи).
находится после того, как
условия будут исследованы; переопределенные задачи имеющие условия, которые не
используются при их решении выбранным способом; неопределенные задачи
недостаток данных в которых не позволит ответить на вопрос задачи).
в) фабула задачи (задачи на «движение», «на работу», «на проценты», задачи на построение, измерение, комбинаторные задачи, логические задачи и т.д.).
Существует не одна классификация, а много разных на основании различных параметров [24, 86].
При обучении математики в начальной школе обучающиеся принимают задачу как специальный текст, в котором обрисована некая житейская ситуация, охарактеризованная численными компонентами [4, 5]. В задачах рассматривают отношения и значения величин и предлагают найти неизвестные значения величин, зависящих от данных и связанных с ними определенными отношениями, указанными в тексте. Поэтому задачи называют арифметическими, текстовыми, сюжетными и вычислительными. Согласно Е.И. Щербаковой, арифметическая задача – это простейшая сугубо математическая форма отображения реальных ситуаций, которые одновременно близки и понятны детям и с которыми они ежедневно сталкиваются [33, 202]. В.Л. Дрозд дополняет, что такие задачи имеют житейское содержание и решаются с помощью арифметических действий [20, 158]. Таким образом, понятия «задача» и «арифметическая задача» в начальном курсе математики не дифференцируются. Задачи формулируют в виде текста, отражающего количественные отношения между реальными объектами [12, 220].
Во время решения арифметических задач у обучающихся развивается ряд мыслительных способностей. Во-первых, развивается способность осознавать и выделять «условие» и «вопрос». Во-вторых, обучающиеся учатся устанавливать связь между величинами и между арифметическими действиями, связывающими их. В-третьих, одновременно с вышесказанным обучающиеся учатся на практике применять имеющиеся вычислительные навыки [8, 58].
Говоря о структурных компонентах арифметической задачи, следует отметить, что в учебных пособиях различных авторов составные части задачи названы по-разному. Так, М.И. Моро, Г.В. Дорофеев в задаче выделяют: условие, вопрос, решение, ответ [21]. А.Л. Чекин выделяет: условие, требование, решение и ответ [30]. А Л.Г. Петерсон называет такие части задачи: условие, вопрос, схема, выражение и ответ [23].
Построение модели задачи является основной частью решения любой текстовой задачи. Исследование данных задачи является средством для решения и получения ответа.
Модель это мысленно представленная и модель или материально реализованная система. Модель задачи может заменять реальные объекты и процессы во время решения. Изучение модели дает информацию об объекте, описанном в задаче. Модель в самом широком смысле - это любой мысленный или знаковый образ моделируемого объекта (оригинала). Моделью может быть изображение, описание, схема, чертеж, график, компьютерная программа, копия оригинала (увеличенные или уменьшенные). Модель должна быть удобна для изучения свойств исследуемого объекта и должна позволить перенести полученные знания на исходный объект. Для решения задачи нужно охватить те свойства модели, которые могут быть важны для решения [24, 67].
Решение текстовых задач осуществляется с использованием следующих методов:
Арифметический;
Алгебраический;
Геометрический;
Логический;
![]() Практический.
Практический.
Содержание каждого метода включает в себя использование различных моделей
Решение задач с использованием арифметического метода – нахождение ответа на требование задачи, выполнив арифметические действия над числами. Одну задачу можно решить разными арифметическими способами. Решение задачи обучающимися будет отличаться связями между данными и искомыми или последовательностью использования этих связей.
Использование построения или свойства геометрической фигуры при решении задач характерно для геометрического метода.
Нахождение ответа на требование задачи при помощи логического рассуждения является основой логического метода.
Выполнение действий с предметами или моделями предметов является практическим методом.
В процессе решения комбинаторных задач в начальных классах часто используется практический метод. Данный метод реализуется через использование модели ситуации, описанной в задаче, при помощи реальных объектов (прием драматизации), предметных или графических моделей (выполнение рисунка), с помощью таблиц и графов («дерево» возможных вариантов). Решение комбинаторных задач представляет собой сложный процесс. Так же комбинаторные задачи можно назвать сюжетными.
Процесс решения задач можно анализировать с разных сторон:
с математической стороны – какие математические операции следует произвести, чтобы получить ответ на требование задачи;
с логической стороны – какие рассуждения надо провести;
с психологической стороны – какие мыслительные операции выполняет решающий задачу;
с педагогической стороны – какие методические приемы формируют у учащихся умения решать задачу [13,133].
Обучению решению задач в начальной школе уделяется огромное внимание. Это обусловлено следующим.
1. В сюжетах задач находят отражение практические ситуации, имеющие место в жизни обучающегося. Способствует осознанию количественных отношений между объектами, углубляет и расширяет представления о действительности.
2. Обучающийся осознает практическую значимость тех знаний и понятий, которыми он владеет в начальной школе.
З. Во время решения задач у обучающегося формируются умения, необходимые для решения любой математической задачи (выделять данные и искомое, условие и вопрос, устанавливать зависимость между ними, строить умозаключения, моделировать, проверять полученный результат).
Общие умения для решения текстовых задач:
готовность обучающихся к знакомству с текстовой задачей предполагает сформированность:
а) навыков чтения;
б) представлений о смысле действий сложения и вычитания, их взаимосвязи, понятий «увеличить (уменьшить) на», разностного сравнения;
в) основных мыслительных операций: анализ и синтез, сравнение;
г) умения описывать предметные ситуации и переводить их на язык схем и математических символов;
д) умения чертить, складывать и вычитать отрезки;
е) умения переводить текстовые ситуации в предметные и схематические модели.
Первый подход предусматривает одновременное ознакомление с задачей (понятие задачи, ее составные части, работа с памяткой и т.д.) и формирование конкретного смысла действий сложения и вычитания (Богданович М.В., Моро М.И., Бантова М.А. и др.). Вводятся задачи с первого класса.
Первая группа подразумевает простые задачи, при решении которых обучающиеся усваивают конкретный смысл каждого из арифметических действий.
1) Нахождение суммы.
2) Нахождение остатка.
3) Нахождение суммы одинаковых слагаемых.
4) Деление на равные части; деление по содержанию.
Вторая группа включает простые задачи, при решении которых обучающиеся усваивают связь между компонентами и результатами арифметических действий. Это простые задачи на нахождение неизвестного компонента.
Третья группа — простые задачи, при решении которых раскрываются понятия разности и кратного отношения [3,156].
Обучение решению задач
каждого вида осуществляется в соответствии ![]() с
логикой построения курса (М.И.Моро), т. е. обучающиеся знакомятся с
соответствующими видами простых задач, приступая к изучению нового
с
логикой построения курса (М.И.Моро), т. е. обучающиеся знакомятся с
соответствующими видами простых задач, приступая к изучению нового ![]() понятия.
Процесс решения простых задач находиться в тесной взаимосвязи с усвоением
математических понятий. Методика обучения решению простых задач включает три
ступени: подготовка, ознакомление, закрепление.
понятия.
Процесс решения простых задач находиться в тесной взаимосвязи с усвоением
математических понятий. Методика обучения решению простых задач включает три
ступени: подготовка, ознакомление, закрепление.
Для решения задач в начальной школе используется аналитический и синтетический способ решения задач. Используя данные способы обучающиеся постепенно сами начинают задавать себе вопросы в определенной последовательности и выполняют рассуждения, связанные с решением задачи.
Основным методом обучения решению составных задач при данном подходе является «показ способов решения определенных видов задач. А встретившись с задачей незнакомого типа, испытывают затруднения при ее решении [21].
До знакомства с задачей учащимся также необходимо приобрести определенный опыт в соотнесении предметных, текстовых схематических и символических моделей, который они смогут использовать для интерпретации текстовой модели.
1.4. Способы формирования у младших школьников учебных действий целеполагания, планирования и прогнозирования при решении арифметических задач
В Федеральном государственном образовательном стандарте начального общего образования прописаны умения, которыми должны овладеть обучающиеся. В сфере регулятивных УУД выпускники должны овладеть следующими типами учебных действий: принятие и сохранение учебной цели, задачи, планирование ее реализации (в том числе во внутреннем плане), контроль и оценка своих действий, внесение соответствующих коррективов в их выполнении».
Термин «формирование» обозначает «процесс становления человека, как социального существа под воздействием определенных факторов: социальных, экономических, психологических, идеологических, воспитания и др.» [11]. Также под формированием понимают процесс целенаправленного и организованного овладения социальными субъектами целостными, устойчивыми чертами и качествами, необходимыми им для успешной жизнедеятельности [22]. Термин «формирование» употребляют тогда, когда речь идет о том, что приобретает обучающийся: понятие, навык, новый вид деятельности [26, 67]. В работе мы будем рассматривать формирование как приобретение субъектом новых качеств, выработку умений, овладение действиями.
Термин «формирование» относится к объектам, качественные изменения которых происходят под влиянием каких-либо внешних управляющих сил [18, 40].
При не стандартной формулировке условия и требования арифметической задачи у учащихся возникают трудности с определением вопроса, т.е. цели деятельности.
Может ли Ваня купить 3 ручки по 4рубля и 4 тетради по 5рублей, если у него всего 45рублей?[21, 54].
Работу над такими задачами следует начинать с переформулировки условия и требования задачи. Они должны быть понятны всем учащимся.
Сформулировав задачу так: «Сколько рублей Ваня потратит на 3 ручки по 4 рубля и 4тетради по 5рублей?», учащиеся легко определяют вопрос задачи, т.е. цель своей деятельности.
Формирование учебного действия планирования при решении задачи может происходить следующим образом.
Сначала план решения строится по образцу, затем ученик сам планирует свою деятельность для достижения цели задания. На первых этапах обучения решению текстовых задач учащиеся строят план в виде вопросов, которые помогают им понять важность последовательных, осознанных действий и способствуют формированию умения последовательно анализировать данные и составлять план решения [16, 10].
Формированию умения строить план решения задачи способствуют такие задания, где ученики должны или выбрать из предложенных схем одну, соответствующую данной задаче, или сами составить схему. Схема поможет не только последовательно проанализировать задачу, но и составить план ее решения.
Задача 4. Маме 32 года, дедушка старше мамы на 30 лет, а бабушка на 3 года моложе дедушки. Сколько лет бабушке? На сколько лет бабушка старше мамы? [21, 52].
Учитель задает вопросы. Эту последовательность вопросов дети постепенно запоминают, что ведет к формированию планирования при решении арифметических задач.
Учитель. Каково требование задачи?
Ученики. Сколько лет бабушке?
Учитель. Каких данных не хватает?
Ученики. Мы не знаем сколько лет дедушке.
Учитель. Сможем ли мы ответить на вопрос задачи, найдя возраст дедушки?
Ученики. Да.
Учитель. Какое требование в задаче еще?
Ученики. На сколько лет бабушка старше мамы?
Учитель. Можем ответить на этот вопрос?
Ученики. Сможем, если найдем возраст бабушки.
Затем выясняется, каким может быть план решения задачи.
1. Узнаю возраст дедушки.
2. Узнаю возраст бабушки
3. Узнаю на сколько бабушка старше мамы.
Учитель. Как в соответствии с этим планом записать решение задачи? Ученики выполняют запись.
1) 32+30=62 года – возраст дедушки;
2) 62 – 3=59лет – возраст бабушки;
3) 59 – 32=27, на 27 лет бабушка старше мамы.
При решении текстовых задач ученикам приходится самостоятельно ориентироваться в имеющихся знаниях, ставя пред собой вопрос: «Владею ли я теми знаниями, которые необходимы для решения задачи? Необходимы и мне новые знания и умения?». Для этой деятельности нужны такие регулятивные учебные действия, как прогнозирование, коррекция и волевая саморегуляция [30].
При работе над формированием учебных целесообразно использовать текстовые задачи с готовыми решениями, где из предложенных решений следует выбрать правильное и обосновать правильность выбора.
Задача 5. В прятки играли 12 ребят. К ним присоединилось 3 девочки и 4мальчика. Сколько всего ребят стали играть в прятки? [21, 27].
Выберите выражении, которое является математической моделью этой задачи.
А) (3+4)+12;
Б)3+4;
В)12+4;
Учащиеся выбирают выражения А.
Таким образом, в процессе обучения решению текстовых задач можно формировать виды учебных действий: целеполагание, планирование, прогнозирование, контроль, коррекцию, оценку и волевую саморегуляцию. Для этого нужны специальные задания. Поэтому при подготовке к уроку, отбирая или специально конструируя задания, учитель должен учитывать не только логику предметного содержания, но и характер того или иного учебного действия которое формируется на данном этапе.
В современной методике процесс решения текстовой задачи рассматривается как переход от словесной модели к математической. В основе осуществления этого перехода лежит семантический (смысловой) анализ текста и выделение в нем математических понятий и отношений (математический анализ текста). При выполнении любого задания (тем более при решении текстовой задачи) важно осознание обучающимся предстоящей деятельности с точки зрения ее учебного смысла. Обучающийся должен задуматься о значении, о цели, что он делает, понять, зачем это необходимо. Поэтому уже первые шаги в решении задачи позволяют развивать действие определения цели предстоящей деятельности.
Для этого при первом знакомстве с арифмиетическими задачами обучающимся можно предложить план, в соответствии с которым они определяют цель своей деятельности.
1.Прочитайте задачу, выделить условие и вопрос (требование).
2. Найдите в условии данные и искомые.
3. Повторите вспомогательную модель задачи.
4. Обдумайте план решения.
5. Запишите решение.
6. Проверьте решение задачи.
7. Напишите ответ [14, 30].
Формированию вышеперечисленных действий сначала обучает учитель, а затем обучающиеся самостоятельно осуществляют план.
Прогнозирование является наиболее трудным в освоении, данное действие предполагает «предвосхищение результата и уровня усвоения знаний, его временных характеристик» [1,29].
Использование прогнозирования на уроках математики связано с предвосхищением результата выполняемых действий, предварительной прикидкой ответа, который необходимо получить при решении задач, уравнений, выполнении измерений.
При работе над текстовой арифметической задачей используется прием прикидки результата, где необходимо определять границы искомого числа. На этапе восприятия и осмысления текста задачи обучающиеся должны определить, больше или меньше какого-либо из данных чисел должен получиться ответ. После решения задачи, проводится сравнение прогноза с полученным результатом. Если прогноз и ответ решения расходится, то выявляется причина, которая связанна с неверным решением задачи. Сопоставив ответ с прогнозом можно обнаружить ошибку и своевременно исправить. Это помогает обучающимся осуществлять самоконтроль и коррекцию ошибок. Такой прием полезен при решении задач.
Задачи на нахождение неизвестного компонента действия. Обучающиеся часто решают такие задачи способом подбора на основе знания состава чисел: они называют правильный ответ, по неверно выбирают арифметическое действие. Прием прикидки ответа помогает увидеть важность правильного выбора действия.
Например, обучающимся дается задача: «В вазе лежало 8 конфет, из них 4 шоколадные, а остальные - карамельки. Сколько карамелек лежало в вазе?» Некоторые обучающиеся называют правильный ответ (4), но записывают неверное решение: 4 + 4 = 8.
Чтобы предупредить данную ошибку перед решением приведенной задачи полезно сделать прикидку ответа, спросив: «В ответе должно получиться число больше или меньше, чем 8?» В случае неверной записи решения нужно вернуться к сделанному прогнозу: «Мы определили, что должно было получиться меньше 8, а получилось 8. Следовательно, задача решена неправильно».
В Стандарте второго поколения прописано, что у обучающихся необходимо формировать умение проводить проверку правильности вычислений путем прикидки и оценки результата действия [29]. Это необходимо выполнить в процессе работы над задачами, связанными с реальными жизненными ситуациями, например: «Бабушка хочет связать внукам носки. На один носок нужно 50 г шерсти. Хватит ли ей 290 г шерсти, чтобы связать носки трем внукам?». Обучающимся необходимо ответить на вопрос и объяснить свой ответ. Они могут рассуждать так: «Для трех внуков нужно связать 6 носков, на это потребуется 300 г шерсти (50 • 6 = 300). Значит, бабушке шерсти не хватит» [1, 33].
Использование в процессе обучения таких задач способствует формированию способности к прогнозированию и позволяет учителю реализовать компетентностный подход в обучении на основе применения обучающимися математических знаний для решения практических задач.
Вывод по первой главе
В первой главе описаны психолого – педагогические особенности детей младшего школьного возраста. К ним относятся: мотивационная, социальная, психологическая и учебная сферы. Были рассмотрены основные новообразования младших школьников, это – познавательное отношение к миру; интеллектуальная рефлексия; восприятие; развитие произвольной и смысловой памяти.
Учебная деятельность является основной деятельностью младших школьников.
Действия целеполагания, планирования и прогнозирования являются частью Регулятивных УУД. Согласно требованиям ФГОС НОО у младших школьников в процессе обучения должны формироваться Регулятивные УУД, которые должны использоваться на каждом уроке.
Формирования универсальных учебных действия происходит во время выполнения различных задания на уроке, в том числе при решении арифметических задач.
В процессе решения арифметических задач у обучающихся формируются учебные действия целеполагание, планирование и прогнозирование.
Глава II. ОПЫТНО-ЭКСПЕРИМЕНТАЛЬНАЯ РАБОТА ПО ФОРМИРОВАНИЮ У МЛАДШИХ ШКОЛЬНИКОВ УЧЕБНЫХ ДЕЙСТВИЙ ЦЕЛЕПОЛАГАНИЯ, ПЛАНИРОВАНИЯ И ПРОГНОЗИРОВАНИЯ ПРИ РЕШЕНИИ АРИФМЕТИЧЕСКИХ ЗАДАЧ
2.1. Диагностика уровня сформированности у младших школьников учебных действий целеполагания, планирования и прогнозирования
Для доказательства выдвинутой гипотезы, проведена экспериментальная работа, состоящая из трех этапов (констатирующий, формирующий и контрольный этапы).
Цель констатирующего этапа – определить уровень сформированности учебных действий целеполагания, планирования и прогнозирования у младших школьников на констатирующем этапе эксперимента.
Задачи этапа:
1)Определить экспериментальную группу, доказать их расположенность.
2)Выбрать диагностический материал.
3)Провести диагностику сформированности у младших школьников учебных действий целеполагания, планирования и прогнозирования и интерпретировать полученные результаты.
Экспериментальная работа проводилась в МОУ «Горекинская ООШ» Улетовского района в течение марта- апреля 2019-2020 учебного года во 2 классе. Всего участвовало 10 учеников. Анализ классных журналов, личных дел учащихся, наблюдение за учащимися на уроках, анализ результатов их деятельности, беседа с учителем и школьниками, позволили определить расположенность группы.
Для выявления исходного уровня сформированности учебных действий целеполагания, планирования и прогнозирования был использован следующий диагностический материал:
1) Методика диагностики уровня развития основ теоретического мышления младших школьников «Логические задачи» (Методика А.З. Зака) (Приложение А);
2) Диагностика особенностей развития поискового планирования (методика А.З.Зака) (Приложение Б);
3) Методика «Лист наблюдений» (Автор: И.С. Нугаева) (Приложение В);
На констатирующем этапе экспериментальной работы диагностика уровня сформированности проводилась во 2 классе в марте - апреле 2019-2020 учебного года. В самом начале исследования для определения уровня сформированности целеполагания у младших школьников была проведена методика диагностики уровня развития основ теоретического мышления младших школьников «Логические задачи» (Методика А.З. Зака). Цель: выявление у учащихся уровня сформированности теоретического анализа и внутреннего плана действий.
Результаты исследования:
1. Уровень развития умения понять учебную задачу
Правильно решено 11 задач и более - высокий уровень.
От 5 до 10 задач - средний уровень.
Менее 5 задач - низкий уровень.
2. Уровень развития умения планировать свои действия
Правильно решены все 22 задачи - высокий уровень.
Не решены последние 4 (т. е. 18-22) - средний уровень.
Менее 10 задач - низкий уровень.
Решены только 1 и 2 задачи - ребенок умеет действовать "в уме" в минимальной степени.
Решена только первая задача - не умеет планировать свои действия, затрудняется даже заменить в "уме" данное отношение величин на обратное, например, отношение "больше" на отношение "меньше".
3. Уровень развития умения анализировать условия задачи
Правильно решены 16 задач и более, в том числе задачи с 5 по 16, - высокий уровень развития.
Задачи с 5 по 16 решены частично (половина и более) - средний уровень.
Задачи с 5 по 16 не решены - низкий уровень развития, ребенок не умеет выделить структурную общность задачи, ее логические связи.
Результаты методики, проведенной на констатирующем этапе представлены в таблице 2.1 (Приложение Г).
Таблица 2.1.
Результаты методики диагностики уровня развития основ теоретического мышления младших школьников «Логические задачи» (Методика А.З. Зака).
|
Параметры
Уровни |
Умение понять учебную задачу |
Умение планировать свои действия |
Умение анализировать условия задачи |
|
Высокий |
40% |
30% |
30% |
|
Средний |
30% |
40% |
30% |
|
Низкий |
30% |
30% |
40% |
Анализ полученных результатов показал, что высокий уровень развития умения понять учебную задачу в опытной группе 40 % - 4обучающихся, средний уровень 30% - 3 обучающихся, низкий уровень 30% - 3обучающихся. Высокий уровень развития умения планировать свои действия в опытной группе 30 % - 3обучающихся, средний уровень 40% - 4обучающихся, низкий уровень 30% - 3обучающихся. Высокий уровень развития умения анализировать условия задачи в опытной группе 30 % - 3обучающихся, средний уровень 30% - 3обучающихся, низкий уровень 40% - 4обучающихся.
Результаты диагностики можно проследить в гистограмме 1.
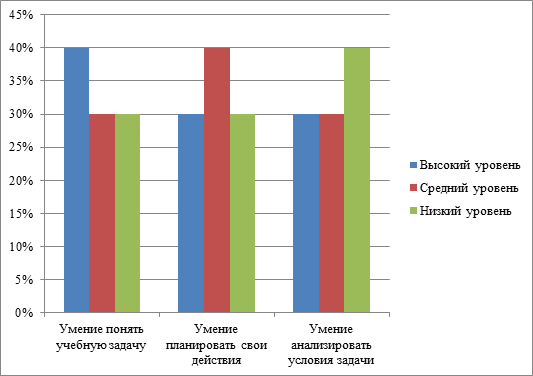
Гистограмма 1. Результаты методики диагностики уровня развития основ теоретического мышления младших школьников «Логические задачи» (Методика А.З. Зака) (%)
Из гистограммы видим, что обучающихся с высоким, средним и низким уровнем развития основ теоретического мышления практически одинаковое количество.
Далее была использована методика «Диагностика особенностей развития поискового планирования» (методика А.З. Зака).
Цель методики: выявить сформированность действия поискового планирования‚ как умения разрабатывать программу выполнения действий для достижения поставленной цели.
Оценивались следующие регулятивные универсальные учебные действия: действия планирования и контроля.
Результаты оценивались по трем уровням планирования представленным в таблице 2.2. (Данные представлены в Приложении Д)
Таблица 2.2.
Критерии и уровни методики «Диагностика особенностей развития поискового планирования» (методика А.З. Зака)
|
Высокий уровень |
Средний уровень |
Низкий уровень |
|
Целостное планирование |
Частичное планирование |
|
|
1 - успешное решение задач № 3 и №4; 2 – успешное решение задач №5 и №6; 3 – успешное решение задач №7 и №8; 4 – успешное решение задач №9 и № 10; 5 – успешное решение задач № 11 и № 12 |
успешное решение задач № 1 и №2. |
успешное решение задач № 1 или №2, ноль решенных задач |
Таблица 2.3.
Результаты методики «Диагностика особенностей развития поискового планирования»
|
Группа |
Уровень сформированности действия поискового планирования |
||
|
Высокий |
Средний |
Низкий |
|
|
Экспериментальная группа |
30 % |
60 % |
10 % |
Во время прохождения диагностического задания, обучающиеся экспериментальной группы сталкивались с трудностями, это связано, прежде всего, с недостаточно развитым действием планирования своей деятельности.
В результате исследования сформированности уровня развития регулятивного действия планирования и контроля в экспериментальной группе‚ было выявлено следующее: более половины учащихся имеют средний показатель уровня развития поискового планирования, так как, следовательно, обладают частичным планированием. Один обучающийся обладают низким уровнем поискового планирования, что составляет 10%. Высокий уровень 30%, сформированности поискового планирования и умения контролировать свою деятельность показали 3 обучающихся. Они успешно решали задачи повышенной сложности, не фиксировали промежуточные результате в бланках, выполняя комбинации задач в уме.
Ниже представлена гистограмма результатов полученных по методике «Диагностика особенностей развития поискового планирования».
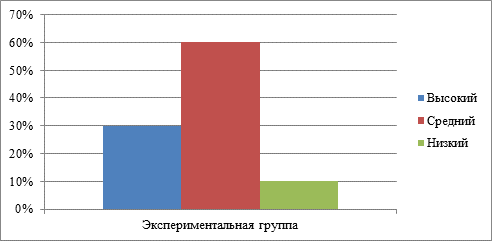
Гистограмма 2. Результаты по методике «Диагностика особенностей развития поискового планирования» (%)
По результатам представленным в гистограмме, можно проследить что в экспериментальной группе преобладают обучающиеся со средним уровнем планирования и контроля своих действий.
Далее использовалась методика «Лист наблюдения». Автор: Нугаева И.С.
Целью данной методики является определение и фиксация уровня сформированности умения прогнозировать при решении задач.
Оцениваемое действие: регулятивное универсальное учебное действие прогнозирования.
Интерпретация данных:
Задача 1 оценивается в 1 балла.
Задача 2 оценивается в 2 балла.
Задача 3 оценивается в 3 балла.
Задача 4 оценивается в 4 балла.
10-7 баллов – высокий уровень сформированности умения прогнозировать.
6-3 баллов – средний уровень сформированности умения прогнозировать.
3-1 балл – низкий уровень сформированности умения прогнозировать.
1-0 баллов – несформированность умения строить прогноз.
Результаты использованного листа наблюдений представлены в таблице 2.4.
Таблица 2.4.
Результаты методики «Лист наблюдений». И.С. Нугаева
|
Группа |
Уровень сформированности умения прогнозировать |
||
|
Высокий |
Средний |
Низкий |
|
|
Экспериментальная группа |
20 % |
30 % |
50 % |
Анализ полученных результатов показал, что высокий уровень сформированности умения прогнозировать в экспериментальной группе 20 % - 2обучающихся, средний уровень сформированности умения прогнозировать у 30 % - 3 обучающихся. У 50 % - 5 обучающихся выявлен низкий уровень сформированности умения прогнозировать.
Результаты диагностики можно проследить в гистограмме 1.
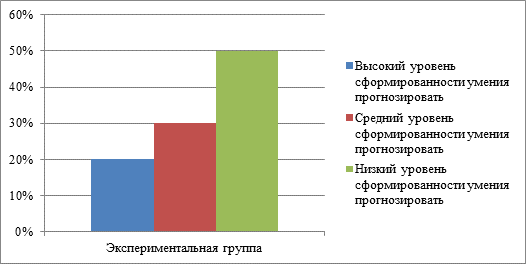
Гистограмма 3. Результаты методики «Лист наблюдения». Автор: И.С. Нугаева (%)
По результатам, представленным на гистограмме 3, видно, что в экспериментальной группе преобладают обучающиеся с низкими показателями сформированности учебного действия прогнозирования.
Подводя итог констатирующего этапа, можно сделать вывод о том, что преобладают обучающиеся со средним уровнем сформированности учебных действий целеполагания, планирования и прогнозирования. Обучающиеся испытывали затруднения при выполнении заданий.
Вышеизложенное позволяет сделать вывод о том что, необходимо провести целенаправленную работу с младшими школьниками по формированию учебных действий целеполагания, планирования и пронозирования.
2.2. Задания, направленные на формирование у младших школьников учебных действий целеполагания, планирования и прогнозирования при решении арифметических задач
Экспериментальная работа на формирующем этапе проводилась в течение марта – апреля 2019-2020 учебного года во 2 классе.
Цель формирующего этапа экспериментальной работы: создать условия для формирования у младших школьников учебных действий целеполагания, планирования и прогнозирования при решении арифметических задач.
Задачи этапа:
1. Разработать комплекс заданий, направленный на формирование у младших школьников учебных действий целеполагания, планирования и прогнозирования при решении арифметических задач.
2. Отслеживать промежуточные результаты и при необходимости оперативно корректировать ход опытно-экспериментальной работы.
В течении марта – апреля 2019-2020года на уроках математики решались задания, способствующие формированию у младших школьников учебных действий целеполагания, планирования и прогнозирования.
В современной методике процесс решения текстовой задачи рассматривается как переход от словесной модели к математической. В основе осуществления этого перехода лежит семантический (смысловой) анализ текста и выделение в нем математических понятий и отношений (математический анализ текста). При выполнении любого задания (тем более при решении текстовой задачи) важно осознание обучающимся предстоящей деятельности с точки зрения ее учебного смысла. Обучающийся должен задуматься о значении, о цели, что он делает, понять, зачем это необходимо. Поэтому уже первые шаги в решении задачи позволяют развивать учебное действие целеполагание.
Для этого при первом знакомстве с текстовыми задачами учащимся можно предложить план, в соответствии с которым они определяют цель своей деятельности.
1.Прочитайте задачу, выделить условие и вопрос (требование).
2. Найдите в условии данные и искомые.
3. Повторите вспомогательную модель задачи.
4. Обдумайте план решения.
5. Запишите решение.
6. Проверьте решение задачи.
7. Напишите ответ [19, 30].
Формированию вышеперечисленных действий сначала обучает учитель, а затем обучающиеся самостоятельно осуществляют план.
Регулятивное действие принятия и понимание учебного задания при решении текстовой задачи представлено во фрагменте урока (Приложение).
Задача 1. В трех букетах всего 15роз. В первом и во втором всего 8 роз, а во втором и третьем 12 роз. Сколько роз в каждом букете?[26, 45].
Учитель. Что нам предстоит сделать, т.е. какова цель решения задачи?
Ученики. Найти вопрос задачи и ответить на него.
Учитель. Найдите данные и искомые.
Ученики. Количество роз, – это данное. Также известно, что в первом и втором букете 8 роз, во втором и третьем 12 роз. Сколько роз в каждом букете – это искомое.
Учитель. Обдумайте и самостоятельно начертите схему к задаче (Рис 2.1. Схема к задаче).
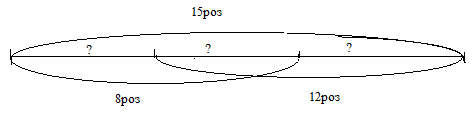
Рис 2.1. Схема к задаче
Учитель. Составьте план решения задачи.
На этом этапе педагог может помочь учащимся, задав вопрос: «Можем ли мы узнать сколько цветов было в первом букете, если знаем что во втором и третьем 12роз?».
Учащиеся составляют план решения задачи.
1.Узнаем сколько роз было в первом букете.
2.Узнаем сколько роз было во втором букете.
3.Узнаем, сколько роз было в третьем букете.
Учитель. Запишите решение задачи по действиям.
Ученики записывают:
1) 15-12=3розы было в первом букете
2) 8-3=5роз во втором букете.
3)12-5=7роз в третьем букете.
Проверка, которая показывает, достигнута ли поставленная цель, осуществляется путем установления соответствия найденного ответа с условием задачи: если в первом букете 3розы, во втором – 5роз, в третьем – 7 роз, то 3+5+7=15роз. Записывается ответ: 3, 5, 7, роз.
При не стандартной формулировке условия и требования текстовой задачи у учащихся возникают трудности с определением вопроса, т.е. цели деятельности.
Задача 2. Может ли Ваня купить 3 ручки по 4рубля и 4 тетради по 5рублей, если у него всего 45рублей?[26, 54].
Работу над такими задачами следует начинать с переформулировки условия и требования задачи. Они должны быть понятны всем учащимся.
Сформулировав задачу так: «Сколько рублей Ваня потратит на 3 ручки по 4 рубля и 4тетради по 5рублей?», учащиеся легко определяют вопрос задачи, т.е. цель своей деятельности.
Формирование другого регулятивного действия – создания плана решения задачи может происходить следующим образом.
Сначала план решения строится по образцу, затем ученик сам планирует свою деятельность для достижения цели задания. На первых этапах обучения решению текстовых задач учащиеся строят план в виде вопросов, которые помогают им понять важность последовательных, осознанных действий и способствуют формированию умения последовательно анализировать данные и составлять план решения [20, 10].
Формированию умения строить план решения задачи способствуют такие задания, где ученики должны или выбрать из предложенных схем одну, соответствующую данной задаче, или сами составить схему. Схема поможет не только последовательно проанализировать задачу, но и составить план ее решения.
Задача 4. Маме 32 года, дедушка старше мамы на 30 лет, а бабушка на 3 года моложе дедушки. Сколько лет бабушке? На сколько лет бабушка старше мамы? [26, 52].
Учитель задает вопросы. Эту последовательность вопросов дети постепенно запоминают, что ведет к формированию регулятивного учебного действия поиска и составления плана решения задачи.
Учитель. Каково требование задачи?
Ученики. Сколько лет бабушке?
Учитель. Каких данных не хватает?
Ученики. Мы не знаем сколько лет дедушке.
Учитель. Сможем ли мы ответить на вопрос задачи, найдя возраст дедушки?
Ученики. Да.
Учитель. Какой требование в задаче еще?
Ученики. На сколько бабушка старше мамы?
Учитель. Можем ответить на этот вопрос?
Ученики. Сможем, если найдем возраст бабушки.
Затем выясняется, каким может быть план решения задачи.
1. Узнаю возраст дедушки.
2. Узнаю возраст бабушки
3. Узнаю на сколько бабушка старше мамы.
Учитель. Как в соответствии с этим планом записать решение задачи? Ученики выполняют запись.
1) 32+30=62 года – возраст дедушки;
2) 62 – 3=59лет – возраст бабушки;
3) 59 – 32=27, на 27 лет бабушка старше мамы.
При решении текстовых задач ученикам приходится самостоятельно ориентироваться в имеющихся знаниях, ставя пред собой вопрос: «Владею ли я теми знаниями, которые необходимы для решения задачи? Необходимы и мне новые знания и умения?». Для этой деятельности нужны такие регулятивные учебные действия, как прогнозирование, коррекция и волевая саморегуляция [32].
При работе над формированием таких регулятивных УУД целесообразно использовать текстовые задачи с готовыми решениями, где из предложенных решений следует выбрать правильное и обосновать правильность выбора.
Задача 5. В прятки играли 12 ребят. К ним присоединилось 3 девочки и 4мальчика. Сколько всего ребят стали играть в прятки? [26, 27].
Выберите выражении, которое является математической моделью этой задачи.
А) (3+4)+12;
Б)3+4;
В)12+4;
Учащиеся выбирают выражения А.
Ниже приведены задания, направленные на формирование учебных действий, рассмотренных в работе.
а) Целеполагание.
Задание №1
Для поездки на дачу на автомобиле израсходовали 14 л бензина, а для поездки на станцию – 3 л. Сколько литров бензина было в баке сначала, если после этих поездок в нем осталось 23 л?
Ответ: 40 литров.
Комментарий. Проверяется способность «удерживать» цель деятельности в ходе решения задачи: ученик должен выполнить арифметические действия.
Задание №2.
В букете у Юли было 35 цветков: ромашки и васильки. На сколько больше было васильков, если ромашек было 15.
Ответ: на 5 васильков больше.
Комментарий. Проверяется способность ставить новые учебные задачи в сотрудничестве с учителем.
Верное выполнение:
1) 35 – 15= 20 васильков
2) 20 – 15= 5 васильков больше, чем ромашек
Ответ: на 5 васильков больше чем ромашек.
Задание №3.
Таня на 3 года младше своей сестры, а вместе им 27 лет. Сколько лет каждой из них?
Ответ: 12 лет Тане, 15 лет сестре.
Комментарий. Проверяется способность «удерживать» цель деятельности в ходе решения учебной задачи.
Верное выполнение:
1) 27-3=24(г)
2) 24:2=12 (л)
3) 12+3=15 (л)
Ответ: 12 лет Тане, 15 лет сестре.
б) Планирование.
Задание№1
В аквариуме было 8 литров воды, когда Женя долил в аквариум несколько литров воды, стало 10 литров воды. Сколько литров воды в аквариум долил Женя?
- О чём задача?
-Что известно?
-Что нужно найти?
- Можем ли мы сразу ответить на главный вопрос задачи?
-Каким действием?
-Почему?
- Запишите решение задачи.
Ответ: долили 2 литра.
Комментарий. В процессе решения задачи обучающиеся учатся решать задачи по предложенному плану.
в) Прогнозирование.
Задание№1
Пакет для продуктов рассчитан на 10 кг. Порвется ли пакет, если в него положить 3 кг 600 г огурцов, 3 кг 200 г моркови и 4 кг 100 г картофеля?
Ответ: пакет порвется.
Комментарий. Проверяется способность предвидеть возможности получения конкретного результата при решении задачи.
Верное выполнение:
2)3 кг 600г + 3 кг 200г + 4 кг 100г = 10кг 900 г
3) 10кг 900г > 10 кг, значит пакет порвется.
Ответ: пакет порвется.
Задание№2
В первую овощную палатку привезли 50кг огурцов, во вторую – на 20кг меньше, а в магазин – столько, сколько в первую и вторую палатку вместе.
Поставь вопрос и реши задачу.
Комментарий. Предложена задача, где отсутствует вопрос. И для того чтобы сформулировать вопрос, нужно предположить какой будет результат.
Верное выполнение:
1) 50 – 20=30кг огурцов во второй палатке.
2) 50+30=80кг огурцов в магазине.
Таким образом, в процессе обучения решению текстовых задач можно формировать целеполагание, планирование и прогнозирование. Для этого нужны специальные задания. Поэтому при подготовке к уроку, отбирая или специально конструируя задания, учитель должен учитывать не только логику предметного содержания, но и характер того или иного УУД, которое формируется на данном этапе.
2.3. Анализ результатов опытно-экспериментальной работы
Экспериментальная работа на контрольном этапе проводилась в марте – апреле 2019-2020 года в 2 классе.
Цель контрольного этапа – определить уровень сформированности учебных действий целеполагания, планирования и прогнозирования у младших школьников на контрольном этапе эксперимента и доказать эффективность формирующего этапа.
Задачи контрольного этапа:
1. Провести повторно диагностику сформированности учебных действий целеполагания, планирования и прогнозирования у младших школьников на констатирующем этапе эксперимента и интерпретировать полученные результаты.
2. Выявить динамику сформированности учебных действий целеполагания, планирования и прогнозирования у младших школьников.
Диагностика сформированности у младших школьников учебного действия целеполагания, планирования и прогнозирования на контрольном этапе проходила аналогично констатирующему этапу экспериментальной работы.
Для исследования итогового уровня сформированности учебных действий целеполагания нами был повторно применен следующий диагностический материал:
1) Методика диагностики уровня развития основ теоретического мышления младших школьников «Логические задачи» (Методика А.З. Зака) (Приложение А);
2) Диагностика особенностей развития поискового планирования (методика А.З.Зака) (Приложение Б);
3) Методика «Лист наблюдений» (Автор: И. С. Нугаева) (Приложение В);
В начале была проведена методика диагностики уровня развития основ теоретического мышления младших школьников «Логические задачи» (Методика А.З. Зака).
Результативность оценивалась в соответствии с критериально-уровневой шкалой описанной в параграфе 2.1.
Результаты диагностики уровня сформированности представлены в таблице 2.5.
Таблица 2.5.
Результаты методики диагностики уровня развития основ теоретического мышления младших школьников «Логические задачи» (Методика А.З. Зака).
|
Параметры
Уровни |
Умение понять учебную задачу |
Умение планировать свои действия |
Умение анализировать условия задачи |
|
Констатирующий этап |
|||
|
Высокий |
40% |
30% |
30% |
|
Средний |
30% |
40% |
30% |
|
Низкий |
30% |
30% |
40% |
|
Контрольный этап |
|||
|
Высокий |
50% |
30% |
50% |
|
Средний |
30% |
50% |
40% |
|
Низкий |
20% |
20% |
10% |
Анализ полученных результатов показал, что высокий уровень умения понять учебную задачу повысился и стал равен 50% - 5 обучающихся. средний уровень 30% - 3 обучающихся, низкий уровень 20% - 2обучающихся. Высокий уровень развития умения планировать свои действия в опытной группе не изменился 30 % - 3обучающихся, повысился средний уровень 50% - 5обучающихся, низкий уровень 20% - 2обучающихся. Высокий уровень развития умения анализировать условия задачи в опытной группе повысился и стал 50 % - 5обучающихся, средний уровень 40% - 4обучающихся, низкий уровень 10% - 1 обучающийся.
Результаты диагностики можно проследить в гистограммах 4-6.
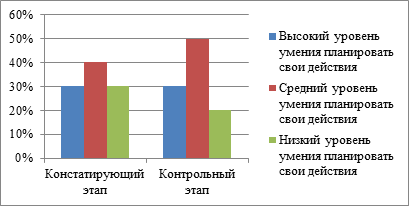
Гистограмма 4. Уровень развития умения понять учебную задачу (%) на констатирующем и контрольном этапе эксперимента
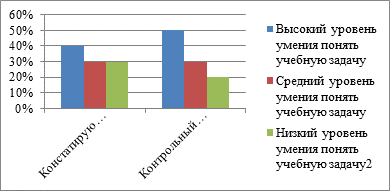
Гистограмма 5. Уровень развития умения планировать свои действия (%) на констатирующем и контрольном этапе эксперимента
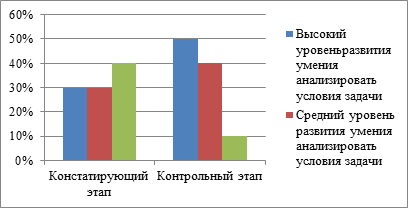
Гистограмма 6. Уровень развития умения анализировать условия задачи (%) на констатирующем и контрольном этапе эксперимента
Таким образом, можно сделать вывод, что целенаправленно проведенная работа на формирующем этапе эксперимента способствовала формированию умения планировать свои действия, понимать учебную задачу, анализировать условия задачи..
На контрольном этапе нами повторно была использована методика «Диагностика особенностей развития поискового планирования» (методика А.З. Зака). Результативность оценивалась в соответствии с критериально-уровневой шкалой описанной в таблице 2.2.
Результаты экспериментальной группы отображены в таблице 2.6 и Гистограмме 8.
Таблица 2.6.
Результаты методики «Диагностика особенностей развития поискового планирования» на констатирующем и контрольном этапе эксперимента
|
Этап эксперимента |
Уровень сформированности действия поискового планирования |
||
|
Высокий |
Средний |
Низкий |
|
|
Констатирующий этап |
30 % |
60 % |
10 % |
|
Контрольный этап |
50% |
40% |
10% |
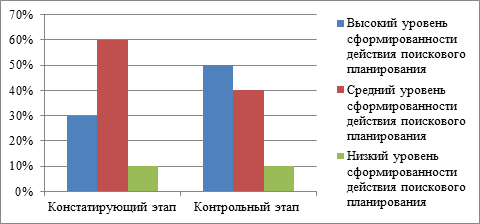
Гистограмма 8. Результаты по методике «Диагностика особенностей развития поискового планирования» (%) на констатирующем и контрольном этапе эксперимента
Анализ результатов диагностики представленных в таблице 2.6 и Гистограмме 8. показывает, что уровень сформированности регулятивного универсального учебного действия планирования и контроля в экспериментальной группе изменился. Средний уровень снизился, на контрольном этапе исследования обучающиеся успешно решали задачи повышенной сложности, выполняя комбинации задач в уме.
Из гистограммы 5 видим что, на констатирующем этапе высокий уровень был у 3 обучающихся (30%), стал у 5 обучающихся (50%). Средний уровень уменьшился. Низкий уровень остался без изменений (10%). Показатели обучающихся улучшились, а это значит, что учащиеся могут грамотно спланировать свою деятельность и осуществлять пошаговый контроль своих действий.
На контрольном этапе эксперимента повторно проведена методика «Лист наблюдений» (автор: И.С. Нугаева). Результативность оценивалась в соответствии с критериально-уровневой шкалой описанной в параграфе 2.1.
Результаты экспериментальной группы отображены в таблице 2.7 и гистограмме 6.
Таблица 2.7.
Результаты Теста простых поручений (Модификация теста «Интеллектуальная лабильность» ППМС – центр «Доверие»)
|
Этап эксперимента |
Уровень сформированности учебного действия прогнозирования |
||
|
Высокий |
Средний |
Низкий |
|
|
Констатирующий этап |
20 % |
30 % |
50 % |
|
Контрольный этап |
30% |
60% |
10% |
По результатам проведенного теста в экспериментальной группе можно проследить, что высокий уровень учебного действия прогнозирования повысился у 1 обучающегося, с высоким уровнем учебного действия прогнозирования стало 3 обучающихся - 30%. Средний уровень сформированности учебного действия прогнозирования так же повысился у двух обучающихся и стал средним у 6 обучающихся - 60%. На контрольном этапе эксперимента низкий уровень сформированности учебного действия пронозирования показал 1 обучающийся (10%).
Результаты методики можно проследить в гистограмме 9.
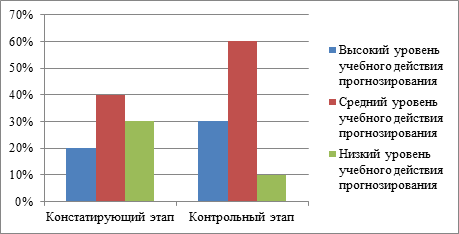
Гистограмма 9. Результаты методики «Лист наблюдений» (Автор: И. С. Нугаева) (%) на констатирующем и контрольном этапе эксперимента
По результатам гистограммы можно сказать, что в экспериментальной группе уровень сформированности учебного действия прогнозирования повысился трех обучающихся, высокий уровень составил 30% - 3 обучающихся, средний уровень 60% - 6 обучающихся.
Вывод по второй главе
Во второй главе описана экспериментальная часть работа, состоящая из трех этапов исследования – констатирующего, формирующего и контрольного. Исследование проходило на базе МОУ «Горекинская ООШ». В экспериментальной группе было 10 обучающихся.
На констатирующем этапе эксперимента проведено исследование по выявлению у обучающихся уровня сформированности учебных действий целеполагания, планирования и прогнозирования при решении арифметических задач.
На формирующем этапе экспериментальной работы были созданы условия для формирования у младших школьников учебных действий целеполагания, планирования и прогнозирования при решении арифметических задач. Были разработаны и апробированы задания, направленные на их формирование на уроке математики.
В ходе контрольного этапа эксперимента проведено повторное диагностирование у обучающихся уровня учебных действий целеполагания, планирования и прогнозирования. После проведения диагностирования, проанализировав результаты констатирующего и контрольного этапов было выявлено, что результаты улучшились.
Таким образом, проделанная экспериментальная работа позволяет утверждать, что работа, направленная на формирование у младших школьников учебных действий целеполагания, планирования и прогнозирования при решении арифметических задач применение специальных заданий дает положительный результат.
ЗАКЛЮЧЕНИЕ
Современное общество не стоит на месте. Развивается наука и техника, появляются новые информационные технологии. На протяжении всей жизни человеку приходится непрерывно чему- то обучаться, а иногда, и овладевать новыми профессиями. Отсюда и встала необходимость конфигураций в образовании. От признания познаний, умений и навыков происходит переход к осмысливанию обучения как процесса подготовки учащихся к настоящей жизни, готовности к тому, чтобы занять активную позицию, успешно решать жизненные задачи, уметь сотрудничать, быть готовым к быстрому переучиванию.
Универсальные учебные действия (УУД) - способность субъекта к саморазвитию и самосовершенствованию путем сознательного и активного присвоения нового социального опыта; совокупность действий обучающегося, обеспечивающих его культурную идентичность, социальную компетентность, толерантность, способность к самостоятельному усвоению новых знаний и умений, включая организацию этого процесса.
Виды УУД: личностные, регулятивные, познавательные, коммуникативные. При формировании регулятивных УУД большая роль отводится математике. В первую очередь она развивает такие свойства интеллекта, как математическая интуиция, логическое, пространственное, техническое и алгоритмическое мышление, способность к конструктивно-математической деятельности.
На современном этапе формирование регулятивных УУД рассматривают такие ученые: Г.В. Бельтюкова, Н.Б. Истомина, М.И. Моро , Л.Г. Петерсон и другие.
В процессе работы над выпускной квалификационной работы мы исследовали учебные действия целеполагание, планирование и прогнозирование. Рассмотрели особенности их формирования в курсе начального образования.
Формированию рассмотренных действий способствует обучение решению арифметическим задачам. Описанные методы и приемы работы с арифметическими задачами способствуют развитию умений ставить цель и придерживаться её, составлять план деятельности, и предполагать, какой результат должен получиться в конце решения.
Перед курсом математики в начальной школе стоят задачи обеспечения числовой грамотности обучающихся в объеме государственного стандарта, развитие логического и образного мышления, воображения, формирование предметных умений и навыков. Они необходимых для успешного решения учебных и практических задач, продолжения образования, развития умения точно и ясно выражать свои мысли, развития смысловой памяти, формирования способности к анализу и синтезу, воспитания интереса к математике, стремления использовать полученные знания в повседневной жизни, освоения основ математических и информационных знаний, формирования первоначальных представлений об этих дисциплинах.
Во второй главе представлены результаты опытно-экспериментальной работы. На констатирующем этапе выявляли уровень сформированности учебных действий целеполагания, планировании и прогнозирования. По результатам исследования на формирующем этапе подобрали методы и приемы формирования у младших школьников учебных действий целеполагания, планирования и прогнозирования В результате проведения контрольного этапа мы выявили, что особую роль в повышении уровня сформированности у младших школьников на уроках математики играют задачи.
В процессе их решения формируются формулировать цель деятельности, составлять план деятельности и прогнозировать результаты, совершенствуются вычислительные навыки, развивается теоретическое мышление и речь обучающихся.
Собственная практическая деятельность показала, что, использование задач на уроках математики, педагог может оказывать достаточно эффективную помощь обучающимся в формировании учебных действий целеполагания, планирования и прогнозирования у младших школьников, о чем свидетельствует положительная динамика опытно – экспериментальной работы.
Список использованных источников
1. Александрова Э. И. Математика. 2 класс. Учеб.: В 2 ч. Ч. 4.2. М.: Бином, 2019. 336 с.
2. Асмолов А.Г. Виды универсальных учебных действий: Как проектировать учебные действия в начальной школе. От действия к мысли / под ред. А. Г. Асмолова. - М.: Академия, 2010. - 338 с.
3. Бантова М. А. Методика преподавания математики в начальных классах [Текст]: учеб. пособие для учащихся школ. отд. пед. уч-щ / М. А. Бантова, Г. В. Бельтюкова. — 3-е изд., испр. - М.: Просвещение, 1984. – 338 с., ил.
4. Белошистая А. В. Обучение решению задач в начальной школе [Текст]: книга для учителя.- М.: «ТИД «Русское слово - РС», 2003. – 288с.
5. Белошистая А.В. Методика начального обучения математике [Текст]: книга для учителя.- М.: «ТИД «Русское слово - РС», 2011. - 288с.
6. Белошистая, А.В. Обучение решению задач в начальной школе [Текст]: книга для учителя/ А.В. Белошистая. - М.: «ТИД «Русское слово - РС», 2003. -288с.
7. Боженкова Л. И., Беребердина, С. П. Универсальные учебные действия и цели обучения математике [Текст] : Стандарты и мониторинг в образовании. М.: Просвещение, 2012. 51с.
8. Бочковская О.Т., Бронникова А.Д. и другие. Решение арифметических задач в начальной школе. Пособие для учителей I-IV классов. Под ред. Пчелко А.С. Академия педагогических наук РСФСР «Учпедгиз», 1949. 214 c.
9. Буданова О.В. Программа формирования универсальных учебных действий на ступени начального общего образования // Завуч начальной школы. 2011. № 5. С. 39–42.
10. Волчегорская Е. Ю., Титаренко Н. Н., Лукьянович, А. К. Особенности оценивания уровня сформированности регулятивных универсальных учебных действий в начальной школе // Стандарты и мониторинг в образовании. 2013. № 4. С. 41–45
11. Иванова, В.А. Педагогика [Электронный ресурс] /В.А. Иванова, Т.В. Левина // Электронный учебно-методический комплекс. – Режим доступа: http://www.kgau.ru/
12. Истомина Н.Б. Методика обучения математике в начальной школе. Развивающее обучение / Н.Б. Истомина. 2-е изд., испр. Смоленск: Изд-во «Ассоциация XXI век», 2009. 288с.
13.
Истомина
Н Б. Методика обучения математике в начальных ![]() классах [Текст] :
учеб. пособие для студ. сред. и высш. пед. учеб. заведений. - 4-е изд.,
стереотип. / НБ. Истомина. —М.: Издательский центр «Академия», 2001-288 с.
классах [Текст] :
учеб. пособие для студ. сред. и высш. пед. учеб. заведений. - 4-е изд.,
стереотип. / НБ. Истомина. —М.: Издательский центр «Академия», 2001-288 с.
14. Истомина Н. Б. Развитие универсальных учебных действий у младших школьников в процессе решения логических задач / Н. Б. Истомина, Н. Б. Тихонова // Начальная школа. – 2011. – №6.– С. 30-34.
15.
Казачкова
СП. Начальная школа. Требования стандартов второго поколения к урокам и
внеурочной деятельности [Текст] ![]() С.П.Казачкова, МС. Умнова. — М: Планета,
2012. — 256 с. — (Качество обучения).
С.П.Казачкова, МС. Умнова. — М: Планета,
2012. — 256 с. — (Качество обучения).
16. Козлова С.А Универсальные учебные действия как основа для формирования предметных математических умений и производная от них. [Текст] / С.А. Козлова // Начальная школа плюс до и после. – 2013 № 10 .- С. 10.
17. Кокорева З. А. Оценочная деятельность в начальной школе: учебно – методическое пособие. Вологда.: Издательский центр ВИРО, 2006. 98с.
18. Кузнецова О.В Формирование регулятивных универсальных учебных действий младших школьников в процессе обучения : дисс. …канд. пед. наук : 13.00.01 / Кузнецова Ольга Владимировна. – Ярославль, 2015. – 283 с.
19. Махотин Д. А. Методические основы формирования УУД // Педагогическая мастерская. Все для учителя. 2014. № 4. С. 4–8.
20. Методика начального обучения математики: учеб. пособие для пед. ин-тов / В.Л. Дрозд, А.Т. Катасонова, Л.А. Латотин и др.; под общей ред. А.А. Столяра и В.Л. Дрозда. М.: Вышэйш. шк., 1988. 254 с.
21. Моро М. И., Бантова М. А., Бельтюкова Г. В. Математика. 2 класс: учебник для общеобразоват. организаций. В 2 ч. Ч. 2. 7-е изд. М.: Просвещение, 2016. 112 с.
22. Национальная энциклопедическая служба [Электронный ресурс] : Формирование. – Режим доступа: http://vocabulary.ru/
24.
Психолого-педагогическое
взаимодействие участников образовательного процесса [Текст] учебник для
академического бакалавриата / ред. И. В. Дубровина. - 5-е изд., испр. и доп. -
М.![]() ЮРАЙТ. - ISBN 978-5-534-03499-8. Ч.
2. - 2017. - 321 с. - (Бакалавр. Академический курс). - ISBN 978-5-534-03522-3
(ч. 2) : 619.00 р. 30. Рабочая программа по математике. З класс [Сост. Т.Н.
Ситникова.- М.: ВАКС), 2015.-80 с.
ЮРАЙТ. - ISBN 978-5-534-03499-8. Ч.
2. - 2017. - 321 с. - (Бакалавр. Академический курс). - ISBN 978-5-534-03522-3
(ч. 2) : 619.00 р. 30. Рабочая программа по математике. З класс [Сост. Т.Н.
Ситникова.- М.: ВАКС), 2015.-80 с.
25. Романович И. Ю. Ведение учета сформированности УУД у младших школьников // Управление начальной школой. 2014. № 1. С. 35-39.
26. Талызина, Н.Ф. Формирование познавательной деятельности младших школьников: Кн. для учителя / Н.Ф. Талызина. – М.: Просвещение, 1988. – 175с.
27. Тужик С. В. От формирования общеучебных умений в подготовке учителя к развитию универсальных учебных действий обучающихся // Методист. 2013. № 3. С. 50-53.
28. Ушаков Д. Н. Большой толковый словарь русского языка. М.: Славянский дом книги, 2014. 960 с.
29. Федеральный государственный образовательный стандарт начального общего образования [Электронный ресурс] // URL: http://минобрнауки.рф/документы/922 (дата обращения 18.07.2020).
30. Чекин А. Л. Математика. 2класс. Учебник. В 2 –х частях. Часть 2. М.: Академкнига, 2017.
31. Чемякина М.А. Методические рекомендации по формированию регулятивных универсальных учебных действий у обучающихся по ФГОС [Текст]: Методическое пособие для учителей, работающих по ФГОС / М. А. Чемякина.: Изд. МАОУ «СОШ №7» г. Краснокамеснк, 2013. – 33 с.
32. Шевцова Е. А . Формирование универсальных учебных действий у младших школьников // Стандарты и мониторинг в образовании. 2013. № 2. С. 28-32.
33. Щербакова Е.И. Методика обучения математике в детском саду: Учеб. пособие для студ. дошк. отд-ний и фак. сред. пед. учеб. заведений. М: ИЦ «Академия», 1998. С. 202-212.
34. Эльконин Д. Б. Психология обучения младшего школьника / Д. Б. Эльконин. – М., 1974. – 302 с.
Приложение А
Методика диагностики уровня развития основ теоретического мышления младших школьников «Логические задачи» (Зак А. 3. Диагностика мыслительной деятельности детей. М., 1993.)
Цель: выявление у учащихся уровня сформированности теоретического анализа и внутреннего плана действий
Возраст: 8 – 9 лет
Методика может иметь как индивидуальное, так и фронтальное использование. Ориентировочное время работы: 30-35 минут.
Инструкция испытуемым:
"Вам даны листы с условиями 22 задач. Посмотрите на них. Первые четыре задачи простые: для их решения достаточно прочитать условие, подумать и написать в ответе имя только одного человека, того, кто, по вашему мнению, будет самым веселым, самым сильным или самым быстрым из тех, о ком говорится в задаче.
Теперь посмотрите на задачи с 5 по 10. В них используются искусственные слова, бессмысленные буквосочетания. Они заменяют наши обычные слова. В задачах 5 и 6 бессмысленные буквосочетания (например, наее) обозначают такие слова, как веселее, быстрее, сильнее и т. п. В задачах 7 и 8 искусственные слова заменяют обычные имена людей, а в задачах 9 и 10 они заменяют все. Когда вы будете решать эти шесть задач, то можете "в уме " (про себя) вместо бессмысленных слов подставлять понятные, обычные слова. Но в ответах задач с 7 по 10 нужно писать бессмысленное слово, заменяющее имя человека.
Далее идут задачи 11 и 12. Эти задачи "сказочные", потому что в них про известных всем нам зверей рассказывается что-то странное, необычное. Эти задачи нужно решать, пользуясь только теми сведениями о животных, которые даются в условии задач.
В задачах с 13 по 16 в ответе нужно писать одно имя, а в задачах 17 и 18 - кто как считает правильным: либо одно имя, либо два. В задачах 19 и 20 обязательно писать в ответе только два имени, а в двух последних задачах - 21 и 22 - три имени, даже если одно из имен повторяется".
Логические задачи:
1. Толя веселее, чем Катя. Катя веселее, чем Алик. Кто веселее всех?
2. Саша сильнее, чем Вера. Вера сильнее, чем Лиза. Кто слабее всех?
3. Миша темнее, чем Коля. Миша светлее, чем Вова. Кто темнее всех?
4. Вера тяжелее, чем Катя. Вера легче, чем Оля. Кто легче всех?
5. Катя наее, чем Лиза. Лиза наее, чем Лена. Кто наее всех?
6. Коля тпрк, чем Дима. Дима тпрк, чем Боря. Кто тпрк всех?
7. Прсн веселее, чем Лдвк. Прсн печальнее, чем Квшр. Кто печальнее всех?
8. Вснк слабее, чем Рпнт. Вснп сильнее, чем Сптв. Кто слабее всех?
9. Мпрн унее, чем Нврк. Нврк унее, чем Гшдс. Кто унее всех?
10. Вшфп клмн, чем Двтс. Двтс клмн, чем Пнчб. Кто клмн всех?
11. Собака легче, чем жук. Собака тяжелее, чем слон. Кто легче всех?
12. Лошадь ниже, чем муха. Лошадь выше, чем жираф. Кто выше всех?
13. Попов на 68 лет младше, чем Бобров. Попов на 2 года старше, чем Семенов. Кто младше всех?
14. Уткин на 3 кг легче, чем Гусев. Уткин на 74 кг тяжелее, чем Комаров. Кто тяжелее всех?
15. Маша намного слабее, чем Лиза. Маша немного сильнее, чем Нина. Кто слабее всех?
16. Вера немного темнее, чем Люба. Вера немного темнее, чем Катя. Кто темнее всех?
17. Петя медлительнее, чем Коля. Вова быстрее, чем Петя. Кто быстрее?
18. Саша тяжелее, чем Миша. Дима легче, чем Саша. Кто легче?
19. Вера веселее, чем Катя, и легче, чем Маша. Вера печальнее, чем Маша, и тяжелее, чем Катя. Кто самый печальный и самый тяжелый?
20. Рита темнее, чем Лиза, и младше, чем Нина. Рита светлее, чем Нина, и старше, чем Лиза. Кто самый темный и самый молодой?
21. Юля веселее, чем Ася. Ася легче, чем Соня. Соня сильнее, чем Юля. Юля тяжелее, чем Соня. Соня печальнее, чем Ася. Ася слабее, чем Юля. Кто самый веселый, самый легкий и самый сильный?
22. Толя темнее, чем Миша. Миша младше, чем Вова. Вова ниже, чем Толя. Толя старше, чем Вова. Вова светлее, чем Миша. Миша выше, чем Толя. Кто самый светлый, кто старше всех и кто самый высокий?
Ключи к тесту:
1. Толя
2. Лиза
3. Вова
4. Катя
5. Катя
6. Коля
7. Лдвк
8. Сптв
9. Мпрн
10. Вшфп
11. Слон
12. Муха
13. Семенов
14. Гусев
15. Нина
16. Вера
17. Коля и Вова
18. Дима и Миша
19. Катя, Маша
20. Нина, Лиза
21. Юля, Ася, Соня
Результаты исследования:
1. Уровень развития умения понять учебную задачу
Правильно решено 11 задач и более - высокий уровень.
От 5 до 10 задач - средний уровень.
Менее 5 задач - низкий уровень.
2. Уровень развития умения планировать свои действия
Правильно решены все 22 задачи - высокий уровень.
Не решены последние 4 (т. е. 18-22) - средний уровень.
Менее 10 задач - низкий уровень.
Решены только 1 и 2 задачи - ребенок умеет действовать "в уме" в минимальной степени.
Решена только первая задача - не умеет планировать свои действия, затрудняется даже заменить в "уме" данное отношение величин на обратное, например, отношение "больше" на отношение "меньше".
3. Уровень развития умения анализировать условия задачи
Правильно решены 16 задач и более, в том числе задачи с 5 по 16, - высокий уровень развития.
Задачи с 5 по 16 решены частично (половина и более) - средний уровень.
Задачи с 5 по 16 не решены - низкий уровень развития, ребенок не умеет выделить структурную общность задачи, ее логические связи.
Бланк для учащихся:
Ф.И.О.__________________________________________________
Возраст_____ Класс_____ Дата заполнения «___» _______ ____г.
1. Толя веселее, чем Катя. Катя веселее, чем Алик. Кто веселее всех?
2. Саша сильнее, чем Вера. Вера сильнее, чем Лиза. Кто слабее всех?
3. Миша темнее, чем Коля. Миша светлее, чем Вова. Кто темнее всех?
4. Вера тяжелее, чем Катя. Вера легче, чем Оля. Кто легче всех?
5. Катя наее, чем Лиза. Лиза наее, чем Лена. Кто наее всех?
6. Коля тпрк, чем Дима. Дима тпрк, чем Боря. Кто тпрк всех?
7. Прсн веселее, чем Лдвк. Прсн печальнее, чем Квшр. Кто печальнее всех?
8. Вснк слабее, чем Рпнт. Вснп сильнее, чем Сптв. Кто слабее всех?
9. Мпрн унее, чем Нврк. Нврк унее, чем Гшдс. Кто унее всех?
10. Вшфп клмн, чем Двтс. Двтс клмн, чем Пнчб. Кто клмн всех?
11. Собака легче, чем жук. Собака тяжелее, чем слон. Кто легче всех?
12. Лошадь ниже, чем муха. Лошадь выше, чем жираф. Кто выше всех?
13. Попов на 68 лет младше, чем Бобров. Попов на 2 года старше, чем Семенов. Кто младше всех?
14. Уткин на 3 кг легче, чем Гусев. Уткин на 74 кг тяжелее, чем Комаров. Кто тяжелее всех?
15. Маша намного слабее, чем Лиза. Маша немного сильнее, чем Нина. Кто слабее всех?
16. Вера немного темнее, чем Люба. Вера немного темнее, чем Катя. Кто темнее всех?
17. Петя медлительнее, чем Коля. Вова быстрее, чем Петя. Кто быстрее?
18. Саша тяжелее, чем Миша. Дима легче, чем Саша. Кто легче?
19. Вера веселее, чем Катя, и легче, чем Маша. Вера печальнее, чем Маша, и тяжелее, чем Катя. Кто самый печальный и самый тяжелый?
20. Рита темнее, чем Лиза, и младше, чем Нина. Рита светлее, чем Нина, и старше, чем Лиза. Кто самый темный и самый молодой?
21. Юля веселее, чем Ася. Ася легче, чем Соня. Соня сильнее, чем Юля. Юля тяжелее, чем Соня. Соня печальнее, чем Ася. Ася слабее, чем Юля. Кто самый веселый, самый легкий и самый сильный?
22. Толя темнее, чем Миша. Миша младше, чем Вова. Вова ниже, чем Толя. Толя старше, чем Вова. Вова светлее, чем Миша. Миша выше, чем Толя. Кто самый светлый, кто старше всех и кто самый высокий?
Приложение Б
Диагностика особенностей развития поискового планирования (методика А.З.Зака )
Цель: выявление сформированности действия поискового планирования как умения разрабатывать программу выполнения действий для достижения поставленной цели.
Оцениваемые УУД: регулятивные действия планирования и контроля, логические действия анализа, синтеза, установления аналогий.
Возраст: ступень начального обучения (8-11 лет).
Форма и ситуация оценивания: групповая и индивидуальная форма.
Далеко не всегда имеет место разработка программы действий. В этом случае каждое действие планируется и сразу же выполняется. Поэтому последующие действия планируются только после выполнения предыдущих. Такая форма планирования квалифицируется как последовательно-частичное планирование. В других случаях разрабатываются и сопоставляются разные варианты всей последовательности требуемых действий. При этом предыдущие действия выполняются лишь после того, как будут намечены все последующие действия. Такая форма планирования квалифицируется как предварительно-целостное планирование.
Для диагностики поискового планирования можно использовать тип задач, в которых для достижения результата требуется выполнить ряд действий. В этом случае можно будет различить уровни развития планирования у детей в зависимости от того, какое количество действий (до выполнения) способен наметить ребенок.
К такому типу относятся задачи «слон—ладья». Смысл их заключается в том, чтобы некоторое расположение объектов преобразовать в другое за определенное количество действий по определенным правилам.
Например, расположение цифр в квадрате «А» нужно преобразовать в расположение тех же цифр, указанное в квадрате «Б» за два действия по следующему правилу: любая цифра за одно действие может переместиться прямо или наискось только в соседнюю свободную клетку:
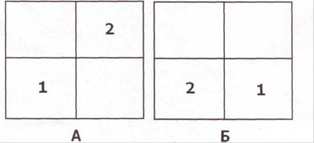
В данной задаче первое действие состоит в перемещении по прямой (ходом шахматной фигуры «ладья») цифры «1», а второе действие связано с перемещением в соседнюю свободную клетку наискось (ходом шахматной фигуры «слон») цифры «2». Усложнение условий планирования при решении таких задач связано как с увеличении числа требуемых операций, так и с возрастанием числа клеток и числа перемещающихся объектов.
Групповое диагностическое исследование для определения различий в планировании у младших школьников строится следующим образом.
Групповое диагностическое исследование для определения различий в планировании у младших школьников строится следующим образом.
1. Психолог, проводящий диагностическое занятие, приходит в класс с комплектом бланков и с чистыми листами бумаги для записи решения задач: на этих листах каждый ребенок пишет свою фамилию и ставит дату проведения занятия.
2. Пока дети подписывают чистые листы, психолог чертит на классной доске два четырехклеточных квадрата:
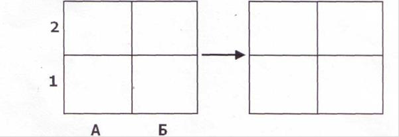
3. Детям говорится: «Сегодня мы будем решать интересные задачи. Посмотрите на эти два квадрата. Каждая клетка в квадрате имеет свое название, которое состоит из буквы и цифры. Эта клетка (следует указать нижнюю левую клетку) называется А1, а эта клетка (указывается правая нижняя) называется Б1, а эти две клетки (верхние две клетки квадрата) называются А2 и Б2».
4. «Теперь решим такую интересную задачу. Сначала три фигурки — круг, треугольник и ромб — были в таких клетках», — психолог рисует указанные фигурки:
«А потом фигурки поменяли свои места и оказались в других клетках», — психолог рисует фигурки в правом квадрате:
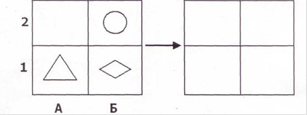
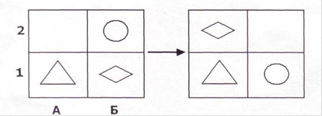
«Нам нужно угадать, узнать, какие два действия, два перемещения сделали фигурки, чтобы попасть в другие клетки. Чтобы решить эту задачу, нужно знать правило: любая фигурка может перемещаться только в свободную соседнюю клетку прямо или наискось. Кто скажет, какое было первое перемещение, какая фигурка первая передвинулась в свободную клетку?... Правильно, первое действие сделал ромб: из клетки Б1 он передвинулся наискось в клетку А2. Запишем это действие, используя названия клеток:
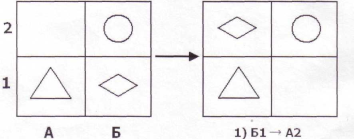
А какое будет второе действие? Правильно, второе действие выполнил круг. Он передвинулся из клетки Б2 прямо в клетку Б1. Запишем второе действие рядом с первым:1)Б1 —> А2; 2)Б2 —> Б1.
5. Вот так решаются задачи на перемещение фигурок из одних клеток в другие. Сейчас я раздам бланки с условиями задач, которые вы будете сегодня решать», — психолог раздает бланки, в каждом из которых даны 12 задач.
6. «Давайте посмотрим на лист с задачами. На самом верху есть задачи №1 и№2. В них нужно отгадать, найти два действия. Затем идут задачи №3 и №4- в них нужно найти 3 действия. Далее в задачах №5 и №6 нужно найти 4действия, в задачах №7 и №8 нужно найти 5 действий, в задачах №9 и №10 -6 действий, в задачах №11 и №12 — 7 действий.
7. Теперь попробуйте сами решить задачу №1 в два действия. Помните наше правило: фигурки перемещаются прямо и наискось в свободную клетку. Подумайте, как перемещались фигурки: какая фигурка передвинулась первой, какая передвинулась второй. Потом запишите эти два действия также, как мы это делали на доске: сначала номер задачи, потом первое действие и второе».
8. Дети решают задачу №1, учитель проходит по рядам и контролирует правильность записи решения.
9. «Давайте проверим теперь решение задачи №1», — учитель на доске рисует условие задачи № 1:
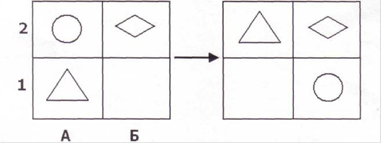
Кто скажет решение?... Верно, первое действие сделал круг, второе —треугольник: №1. 1) А2 —> Б1; 2) А1 —> А2.
10. Теперь решайте задачу №2, — в ней тоже нужно найти 2 действия». Дети решают задачу, психолог контролирует работу детей.
11. «Давайте проверим решение задачи №2», — учитель рисует на доске условие задачи:
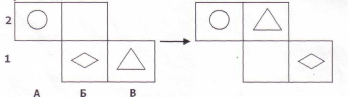
12. «Кто скажет решение этой задачи? Верно, первое действие: треугольник переместился из клетки Б1 в В1. Запишем эти два действия:
№2. 1) В1 →Б2;2) Б1→ В1.
13. Вот так решаются и записываются действия в наших задачах. Теперь сами и уже без проверки решайте все задачи подряд: №№3, 4 и т.д., кто сколько успеет. Только помните правило: фигурки перемещаются прямо и наискось в соседнюю свободную клетку. На бланке с задачами ничего писать нельзя: ни точки, ни линии. Нужно просто смотреть на условия задач и думать, какие перемещения сделали фигурки из одних клеток в другие». Последнее требование, — не касаться бланка ручкой или карандашом, — принципиально важно для диагностики планирования, поскольку проверяется развитие способности действовать «в уме», в мысленном плане, в представлении, т.е. без фиксирования промежуточных результатов на бумаге, например, в виде точки на клетке с той или иной фигуркой или проведения линий, указывающих на возможные перемещения фигурок.
14. На инструктирование детей отводится (в зависимости от возраста) 10-15минут, а на самостоятельное решение задач №№ 3 - 12 должно быть потрачено ровно 20 минут. По истечении этого времени бланки и листы с ответами (кто, сколько успел решить) собираются.
Критерии и уровни оценки планирования:
Протяженность последовательности действий (количество действий), спланированная ребенком.
Обработка результатов
Результаты решения задач, находящиеся на листах бумаги с фамилиями детей, можно обрабатывать, сверяясь с ключом, где представлены правильные действия к каждой задаче.
Диагностическое задание включает задачи двух видов. К первому относятся задачи, решение которых может быть достигнуто с помощью частичного планирования, — это задачи №№ 1 и 2, — поскольку выбор первого действия однозначен, и его наметка и выполнение не связаны с наметкой и выполнением второго действия.
Ко второму виду относятся задачи, решение которых предполагает осуществление целостного планирования, это задачи № 3 - 12, поскольку выбор первого действия неоднозначен. Последнее означает, что правильный выбор первого действия влияет на возможность решить задачу за требуемое число действий, и поэтому наметку первого действия следует проводить одновременно с наметкой всех остальных действий.
Уровни планирования:
Частичное планирование:
Успешное решение задач № 1 и №2
Целостное планирование:
1 - успешное решение задач № 3 и №4
2 – успешное решение задач №5 и №6
3 – успешное решение задач №7 и №8
4 – успешное решение задач №9 и № 10
5 – успешное решение задач № 11 и № 12
В целом, таким образом, проведение группового диагностического занятия с детьми 7-10 лет позволяет выделить тех, кто обладает либо только частичным планированием (при решении лишь двух первых задач), либо разными уровнями развития целостного планирования, — при успешном решении, соответственно, задач №№ 1 - 4; 1 - 6; 1 - 8; 1 - 10; 1 –12.
Приложение В
«Лист наблюдения». Автор: Нугаева И.С.
Цель: определить и зафиксировать уровень сформированности умения прогнозировать при решении задач.
Оцениваемое действие: регулятивное универсальное учебное действие прогнозирования.
Инструкция: В качестве респондентов выступают обучающиеся 2 класса. Учитель осуществляет наблюдение за решением задач индивидуально. Во время беседы обучающийся решает 4 задачи, которые усложняются с использованием действия прогнозирования. Учитель делает пометки в листе наблюдений с какими заданиями справился ученик и проводит интерпретацию данных.
Интерпретация данных:
Задача 1 оценивается в 1 балла.
Задача 2 оценивается в 2 балла.
Задача 3 оценивается в 3 балла.
Задача 4 оценивается в 4 балла.
10-7 баллов – высокий уровень сформированности умения прогнозировать.
6-3 баллов – средний уровень сформированности умения прогнозировать.
3-1 балл – низкий уровень сформированности умения прогнозировать.
1-0 баллов – несформированность умения строить прогноз.
Задача 1.
Посмотрите на ломаные, предположите какая из них длиннее. Объясните, почему вы так считаете. Измерьте при помощи линейки ломаные. Подтвердилось ли ваше предположение.

Рисунок 1 - Ломаные
Задача 2.
«Мама хочет сшить дочкам костюмы. На один нужно 100см ткани. Хватит ли ей 170см, чтобы сшить двум дочкам платья?» Подтвердите свое предположение решением.
Задача 3. Реши задачу с рассуждением и записью решения.
В корзине лежало 15 яблок и груш. Груш было 8. Сколько яблок лежало в корзине.
Задача 4. Прослушайте задачи, предположите, какая сложнее, определите почему. Постройте краткую запись к задаче в виде схемы. Решите задачи. Определите, верно ли вы выбрали задачу, которую решить сложнее.
а) На зиму заготовили 173 кг овощей; моркови, свеклы и капусты. Капусты и моркови было 122 кг. Сколько заготовили свеклы и сколько моркови, если капусты было 62кг?
б) На зиму заготовили 173 кг овощей моркови, свеклы и капусты. Капусты и моркови было 122кг, а моркови и свеклы —100 кг. Сколько заготовили овощей каждого вида [10]?
Приложение Г
Таблица
Результаты методики диагностики уровня развития основ теоретического мышления младших школьников «Логические задачи» (Методика А.З. Зака) на констатирующем этапе.
|
Респондент |
Умение понять учебную задачу |
Умение планировать свои действия |
Умение анализировать условия задачи
|
|
Ученик 1 |
высокий |
высокий |
высокий |
|
Ученик 2 |
средний |
низкий |
средний |
|
Ученик 3 |
низкий |
средний |
средний |
|
Ученик 4 |
высокий |
высокий |
высокий |
|
Ученик 5 |
средний |
высокий |
низкий |
|
Ученик 6 |
низкий |
средний |
низкий |
|
Ученик 7 |
высокий |
средний |
низкий |
|
Ученик 8 |
средний |
низкий |
средний |
|
Ученик 9 |
низкий |
низкий |
низкий |
|
Ученик 10 |
высокий |
средний |
высокий |
Приложение Д
Таблица
Результаты проведения методики А.З. Зака «Диагностика особенностей развития поискового планирования» на констатирующем этапе
|
Респондент |
Результат |
|
Ученик 1 |
Высокий уровень сформированности внимания и самоконтроля |
|
Ученик 2 |
Средний уровень сформированности внимания и самоконтроля |
|
Ученик 3 |
Высокий уровень сформированности внимания и самоконтроля |
|
Ученик 4 |
Средний уровень сформированности внимания и самоконтроля |
|
Ученик 5 |
Средний уровень сформированности внимания и самоконтроля |
|
Ученик 6 |
Средний уровень сформированности внимания и самоконтроля |
|
Ученик 7 |
Средний уровень сформированности внимания и самоконтроля |
|
Ученик 8 |
Средний уровень сформированности внимания и самоконтроля |
|
Ученик 9 |
Высокий уровень сформированности внимания и самоконтроля |
|
Ученик 10 |
Низкий уровень сформированности внимания и самоконтроля |
Приложение Е
Таблица
Результаты методики «Лист наблюдений» (Автор И.С. Нугаева) на констатирующем этапе
|
Респондент |
Результат |
|
Ученик 1 |
Высокий уровень сформированности учебного действия прогнозирования |
|
Ученик 2 |
Средний уровень сформированности учебного действия прогнозирования |
|
Ученик 3 |
Высокий уровень сформированности учебного действия прогнозирования |
|
Ученик 4 |
Низкий уровень сформированности учебного действия прогнозирования |
|
Ученик 5 |
Средний уровень сформированности учебного действия прогнозирования |
|
Ученик 6 |
Низкий уровень сформированности учебного действия прогнозирования |
|
Ученик 7 |
Средний уровень сформированности учебного действия прогнозирования |
|
Ученик 8 |
Низкий уровень сформированности учебного действия прогнозирования |
|
Ученик 9 |
Низкий уровень сформированности учебного действия прогнозирования |
|
Ученик 10 |
Низкий уровень сформированности учебного действия прогнозирования |
Приложение Ж
Фрагмент урока на тему «Закрепление изученного»
Тема урока: Закрепление изученного
|
Этап урока |
Деятельность учителя |
Деятельность обучающихся |
|
Закрепление
|
№ 8 (стр.94) Прочитайте задачу и найдите главные слова для краткой записи.
Составьте краткую запись
Сделай схематический рисунок к задаче.
Решите задачу.
Составь задачи обратные данной и реши.
|
Читают задачу. Было, израсходовали, осталось. Было – ? Израсходовали – 14л и 3л. Осталось – 23л.
14+3+23=40л. Ответ: 40литров бензина было. |
Приложение З
Фрагмент урока на тему «Умножение и деление»
Тема: «Умножение и деление»
|
Этап урока |
Деятельность учителя |
Деятельность обучающихся |
|
Первичное усвоение новых знаний
Первичное осмысление и закрепление
|
Рассмотрите рисунок. Сколько букетов на рисунке? Сколько цветов в каждом букете? По данному рисунку составьте три математические записи. Запись: 5 · 4 = 20 20 : 4 = 5 20 : 5 = 4. – Объясните, что обозначает запись 5 · 4 = 20. (Сколько всего цветов в четырех букетах, если в каждом букете 5 цветов.) – Рассмотрите вторую и третью записи. Чем является число 20 для произведения чисел 5 и 4? – Что получится, если значение произведения разделить на один из множителей? Учащиеся формулируют правило: Если значение произведения разделить на один из множителей, то получится другой множитель. Если значение частного умножить на делитель, то получится делимое. 1. Для данных табличных случаев умножения составьте и запишите соответствующие случаи деления. Поменяйтесь тетрадями, проверьте работы друг друга.
3 · 4 = 12 6 · 5 = 30 7 · ? = 21 12 : 3 = 4 30 : 6 = 5 21 : 7 = 3 12 : 4 = 3 30 : 5 = 6 21 : 3 = 7
8 · 9 = 72 9 · 9 = 81 72 : 8 = 9 81 : 9 = 9 72 : 9 = 8 Сформулируйте правило, как найти неизвестный множитель. 2. Составь задачу, решением которой будет произведение 5∙6 Учащиеся составляют задачу, решением которой будет произведение 5 · 6. Запись:
Решение: 5 · 6 = 30 (р.) – стоят 6 булочек. Ответ: 30 рублей. – Составьте обратные задачи и решите их. Запись: а)
Решение: 30 : 5 = 6 (шт.) – купили. Ответ: 6 булочек. |
|
Приложение И
Фрагмент урока на тему «Закрепление изученного Решение задач»
Тема: «Закрепление изученного. Решение задач»
|
Этап урока |
Деятельность учителя |
Деятельность обучающихся |
|
Закрепление |
№1 (стр. 106) Прочитайте задачу. Одна из книг стоит 20 р., а другая – на 6 р. дороже. Сколько стоят обе книги? (Работа по плану) Составьте краткую запись
Сделайте схематический рисунок к решению задачи
Имея схему, можем ли мы решить задачу? Что найдем первым действием? Вторым действием?
Почему в процессе решения оба раза использовали сложение? |
Читают
Да Стоимость второй книги. Стоимость обеих книг. 1) 20+6=26р. 2) 20+26=46р. Ответ: 46рублей стоят две книги. Для того чтобы узнать стоимость второй книги и всей покупки. |
Приложение К
Таблица
Результаты методики диагностики уровня развития основ теоретического мышления младших школьников «Логические задачи» (Методика А.З. Зака) на контрольном этапе.
|
Респондент |
Умение понять учебную задачу |
Умение планировать свои действия |
Умение анализировать условия задачи
|
|
Ученик 1 |
высокий |
высокий |
высокий |
|
Ученик 2 |
средний |
низкий |
средний |
|
Ученик 3 |
низкий |
средний |
средний |
|
Ученик 4 |
высокий |
высокий |
высокий |
|
Ученик 5 |
средний |
высокий |
низкий |
|
Ученик 6 |
низкий |
средний |
низкий |
|
Ученик 7 |
высокий |
средний |
низкий |
|
Ученик 8 |
средний |
низкий |
средний |
|
Ученик 9 |
низкий |
низкий |
низкий |
|
Ученик 10 |
высокий |
средний |
высокий |
Приложение Л
Таблица
Результаты проведения методики А.З. Зака «Диагностика особенностей развития поискового планирования» на контрольном этапе
|
Респондент |
Результат |
|
Ученик 1 |
Высокий уровень сформированности внимания и самоконтроля |
|
Ученик 2 |
Средний уровень сформированности внимания и самоконтроля |
|
Ученик 3 |
Высокий уровень сформированности внимания и самоконтроля |
|
Ученик 4 |
Средний уровень сформированности внимания и самоконтроля |
|
Ученик 5 |
Высокий уровень сформированности внимания и самоконтроля |
|
Ученик 6 |
Средний уровень сформированности внимания и самоконтроля |
|
Ученик 7 |
Высокий уровень сформированности внимания и самоконтроля |
|
Ученик 8 |
Средний уровень сформированности внимания и самоконтроля |
|
Ученик 9 |
Высокий уровень сформированности внимания и самоконтроля |
|
Ученик 10 |
Низкий уровень сформированности внимания и самоконтроля |
Приложение М
Таблица
Результаты методики «Лист наблюдений» (Автор И.С. Нугаева) на контрольном этапе
|
Респондент |
Результат |
|
Ученик 1 |
Высокий уровень сформированности учебного действия прогнозирования |
|
Ученик 2 |
Средний уровень сформированности учебного действия прогнозирования |
|
Ученик 3 |
Высокий уровень сформированности учебного действия прогнозирования |
|
Ученик 4 |
Средний уровень сформированности учебного действия прогнозирования |
|
Ученик 5 |
Средний уровень сформированности учебного действия прогнозирования |
|
Ученик 6 |
Низкий уровень сформированности учебного действия прогнозирования |
|
Ученик 7 |
Высокий уровень сформированности учебного действия прогнозирования |
|
Ученик 8 |
Средний уровень сформированности учебного действия прогнозирования |
|
Ученик 9 |
Средний уровень сформированности учебного действия прогнозирования |
|
Ученик 10 |
Средний уровень сформированности учебного действия прогнозирования |
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.