СОДЕРЖАНИЕ

 

ВВЕДЕНИЕ. 3

ГЛАВА 1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИЗУЧЕНИЯ ТЕМЫ «ПРОГРЕССИИ В ШКОЛЬНОМ КУРСЕ МАТЕМАТИКИ». 5

1.1 Теоретические основы изучения темы «Арифметическая и геометрическая прогрессии». 5

1.2 Анализ учебно-методической литературы.. 16

1.3. Математический аппарат арифметической и геометрической прогрессии. 20

ГЛАВА 2. МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ ПО ПРИМЕНЕНИЮ ПРАКТИКО- ОРИЕНТИРОВАННЫХ ЗАДАЧ ПО ТЕМЕ «ПРОГРЕССИЯ» НА УРОКАХ МАТЕМАТИКИ.. 21

2.1 Задачи практической направленности по теме «Прогрессия». 21

2.2 Методические рекомендации по применению составленных задач на уроках математики 9 класса. 23

ЗАКЛЮЧЕНИЕ. 31

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ. 33

 

 

 

 

ВВЕДЕНИЕ

 

Актуальность темы заключается в том, что тема «Прогрессии» в курсе алгебры изучается обособленно, лишь в девятом классе, не связана с другими разделами школьной программы по математике. Но несмотря на это задачи, для решения которых необходимо знать не только формулы п-го члена и суммы первых п членов, но и свойства арифметической и геометрической прогрессий, предлагаются на государственной итоговой аттестации в форме ОГЭ. Поэтому теоретические и практические исследования по данной теме представляются актуальными в настоящее время.

Объектом исследования является учебно-воспитательный процесс в общеобразовательной организации.

Предмет исследования – методические особенности по применению практико-ориентированных задач по теме «Прогрессии» в курсе математики в 9 классах.

Oсновной целью данной итоговой аттестационной работы является выявление методических особенностей при изучении темы: «Прогрессии» в школьном курсе математики

Для дocтижения цели реaлизуютcя cледующие зaдaчи:

¾               анализ учебно-методической литературы по проблеме исследования;

¾               проведение логико-дидактического анализа темы «Прогрессии» в школьном курсе математики;

¾               выделение методических особенностей темы «Прогрессии» в школьном курсе математики;

¾               проведение опытно-экспериментальной работы по изучению тем «Алгебраическая прогрессия» и «Геометрическая прогрессия» с учетом методических особенностей;

¾               подведение итогов эксперимента;

¾               разработка планов – конспектов уроков для учителей по теме.

Для достижения целей работы, проверки гипотезы и решения выше поставленных задач были использованы следующие методы:

¾               изучение опыта учителей математики;

¾               наблюдение за учащимися во время проведения занятий.

Теоретическая значимость исследования состоит в следующем: выделить методические особенности изучения темы «Прогрессии» в школьном курсе алгебры, выявить успешность параллельного метода как условия повышения коэффициента усвояемости.

Практическая значимость исследования: разработанные план-конспекты уроков можно предложить учителям математики при изучении темы «Прогрессии» в курсе алгебры 9 класса.

Структура аттестационной работы состоит из введения, двух глав, разбитых на параграфы, заключения, списка использованной литературы и приложения.

 

 

ГЛАВА 1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИЗУЧЕНИЯ ТЕМЫ «ПРОГРЕССИИ В ШКОЛЬНОМ КУРСЕ МАТЕМАТИКИ»

 

1.1 Теоретические основы изучения темы «Арифметическая и геометрическая прогрессии»

 

Задачи на прогрессии, дошедшие до нас из древности, были связаны с запросами хозяйственной жизни: распределение продуктов, деление наследства и др.

Понятие числовой последовательности возникло и развивалось задолго до создания учения о функциях.

На связь между прогрессиями первым обратил внимание великий Архимед (ок. 287 – 212 гг. до н.э.).

Термин «прогрессия» был введён римским автором Боэцием (в 6 веке) и понимался в более широком смысле, как бесконечная числовая последовательность. Название «арифметическая» и «геометрическая» были перенесены из теории непрерывных пропорций, которыми занимались древние греки. 

Формула суммы членов арифметической прогрессии была доказана древнегреческим учёным Диофантом (в 3 веке). Формула суммы членов геометрической прогрессии дана в книге Евклида «Начала» (в 3 веке до н.э.). Правило нахождения суммы членов произвольной арифметической прогрессии впервые встречается в сочинении «Книга абака» в 1202г. (Леонардо Пизанский).

В XVIII веке в английских учебниках появились обозначения арифметической и геометрической прогрессии: арифметическая, геометрическая.

Значительное количество задач на прогрессии имеется в первом учебнике в России «Арифметика»- Л.Ф.Магницкого (1703 год), который в течение полувека был учебником по математике на Руси, его называл «вратами учёности» М.В.Ломоносов. Прогрессии в «Арифметике» Л.Ф.Магницкого включены в пятую часть книги «О прогрессиях и радиксах квадратных и кубических». Вот некоторые их них.

Я.И.Перельман автор большого количества занимательных книг, в которых тоже есть задачи на прогрессии. Вот одна из них. Удивительно, как быстро разбегаются по посёлку слухи! Иной раз не пройдет и двух часов со времени какого–ни будь происшествия, которое видели всего несколько человек, а новость уже облетела весь посёлок: все о ней знают, все слышали. 

Даже в литературе мы встречаемся с математическими понятиями. Так, вспомним строки из «Евгения Онегина».  «… Не мог он ямба от хорея, как мы не бились отличить …».

Ямб - это стихотворный размер с ударением на чётных слогах 2, 4, 6, 8,…стиха.  Номера   ударных слогов образуют арифметическую прогрессию с первым членом 2 и разность прогрессии 2.

Хорей -  это стихотворный размер с ударением на нечётных слогах стиха.  Номера   ударных слогов образуют арифметическую прогрессию 1, 3, 5, 7, …

Будем выписывать в порядке возрастания положительные четные числа. Первое такое число равно 2, второе 4, третье 6 и т.д. Получим последовательность 2, 4, 6, ….

Очевидно, что на четвертом месте этой последовательности будет число 8, на десятом - число 20 и т.д. Вообще для любого номера n можно указать соответствующее ему положительное четное число, оно равно 2n.

Рассмотрим еще одну последовательность. Будем выписывать в порядке убывания правильные дроби с числителем, равным 1:

 

 

Для любого номера nмы можем узнать соответствующую ему дробь; она равна  .

Числа, образующие последовательность, называют соответственно первым, вторым и т.д. членами последовательности. Члены последовательности обычно обозначают буквами с индексами, указывающими порядковый номер члена. Например, и т.д. (читают: “a первое, a второе, a третье ” и т.д.). Вообще член последовательности с номером n, или, как говорят, n-й член последовательности, обозначают . Саму последовательность будем обозначать так:().

Заметим, что последовательность может содержать конечное число членов. В таком случае её называют конечной. Примером конечной последовательности служит последовательность двухзначных чисел: 10; 11; 12; 13; ...; 98; 99.

Чтобы задать последовательность, нужно указать способ, позволяющий найти член последовательности с любым номером.

Часто последовательность задают с помощью формулы, выражающей её n-й член как функцию номера n. Такую формулу, называют формулойn-го члена последовательности. Например, последовательность положительных четных чисел можно задать формулой , а последовательность правильных дробей с числителем, равным 1, - формулой .

Пример 1. Пусть последовательность задана формулой . Вычислим первые пять её членов.

Подставляя вместо n натуральные числа 1, 2, 3, 4, 5, получаем:  

Пример 2. Пусть первый член последовательности () равен 3, а каждый следующий член равен квадрату предыдущего, т.е.  

С помощью формулы  можно по известному первому члену последовательности вычислить второй, затем по известному второму найти третий и т.д. Получим последовательность

Формулу, выражающую любой член последовательности, начиная с некоторого, через предыдущие (один или несколько), называют рекуррентной(от латинского слова recurro - возвращаться) [12, с. 234].

Рассмотрим последовательность натуральных чисел, которые при делении на 4 дают в остатке 1:  … . Каждый её член, начиная со второго, получается прибавлением к предыдущему члену числа 4. Эта последовательность является примером арифметической прогрессии.

Определение. Арифметической прогрессией называется последовательность, в которой каждый член, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.

Иначе говоря, последовательность () - арифметическая прогрессия, если для любого натурального nвыполняется условие:

, (1)

где d - некоторое число.

Из определения арифметической прогрессии следует, что разность между любым её членом, начиная со второго, и предыдущим членом равна d, т.е. при любом натуральном n верно равенство: .

Число dназывают разностью арифметической прогрессии.

Чтобы задать арифметическую прогрессию, достаточно указать первый её член и разность.

Приведем примеры.

Пример 1. Если  и , то получим арифметическую прогрессию: 1; 2; 3; 4; 5; … , члены которой - последовательные натуральные числа.

Пример 2. Если  и , то получим арифметическую прогрессию: 1; 3; 5; 7; 9; … , которая является последовательностью положительных нечетных чисел.

Пример 3. Если  и , то заданная арифметическая прогрессия: - 2; - 4; 0; 8; 10; … является последовательностью отрицательных четных чисел.

Пример 4. Если  и , то имеем арифметическую прогрессию: 7; 7; 7; … , все члены которой равны между собой.

Зная первый член и разность арифметической прогрессии, можно найти любой ее член, вычисляя последовательно второй, третий, четвертый и т. д. члены. Но для нахождения члена прогрессии с большим номером такой способ неудобен. Постараемся отыскать способ, требующий меньшей вычислительной работы.

По определению арифметической прогрессии

 

 

Точно так же находим, что  и вообще, чтобы найти нужно к прибавить  т. е.

 

 

Мы получили формулу n-го члена арифметической прогрессии. Докажем ее методом математической индукции.

1.       При  эта формула верна:

2.       Предположим, что формула (2) верна при   т.е. .

3.       По определению арифметической прогрессии . Подставляя сюда выражение для k-го члена, получим , а это есть формула (2) при .

Из принципа математической индукции следует, что формула (2) верна для любого натурального п.

Что и требовалось доказать.

Приведем примеры решения задач с использованием этой формулы.

Пример 1. Последовательность  - арифметическая прогрессия, в которой  и . Найдем десятый и сотый член этой прогрессии.

Имеем:

.

Формулу n-го члена арифметической прогрессии  можно записать иначе: .

Отсюда ясно, что любая арифметическая прогрессия может быть задана формулой вида , где - некоторые числа.

Верно и обратное: последовательность ,  заданная формулой вида , где - некоторые числа, является арифметической прогрессией.

Действительно, найдем разность го и n-го членов последовательности :

 

 

Значит, при любом n справедливо равенство , и по определению последовательность  является арифметической прогрессией. Заметим, что разность этой прогрессии равна k.

Свойства арифметической прогрессии.

. Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому его соседних членов, т.е. при  верной является формула

(3)

Действительно, при  имеем  и . Складывая почленно эти равенства, получим , откуда следует (3).

. У конечной арифметической прогрессии  сумма членов, равноотстоящих от ее концов, равна сумме крайних членов, т.е. для  верной является формула

 (4)

Действительно, в конечной арифметической прогрессии  члены  и  равноотстоят от концов. По формуле (2)  и  Сумма этих членов равна  и равна сумме крайних членов .

Пусть требуется найти сумму первых ста натуральных чисел. Покажем, как можно решить, эту задачу, не выполняя непосредственного сложения чисел.

Обозначим искомую сумму через S и запишем ее дважды, расположив в первом случае слагаемые в порядке возрастания, а во втором - в порядке убывания: S = 1 + 2 + 3 + … + 98 + 99 + 100,

S= 100 + 99 + 98 + … + 3 + 2 + 1.

Каждая пара чисел, расположенных друг под другом, в сумме дает 101. Число таких пар равно 100. Поэтому, сложив равенства почленно, получим:

Итак, 1+ 2 + 3 + …+ 99 + 100 = 5050.

С помощью аналогичных рассуждений можно найти сумму первых членов любой арифметической прогрессии.

Сумма членов конечной арифметической прогрессии равна произведению полусуммы крайних членов на число членов, т.е. если , то (5)

Действительно, если , то

.

Складывая почленно эти равенства и используя свойство 2, получаем , откуда следует формула (5) [25].

Пример 1. Найдем сумму первых двадцати членов арифметической прогрессии 1; 3,5; ... .

В данной арифметической прогрессии . По формуле n-го члена найдем двадцатый член прогрессии:

Теперь вычислим сумму первых двадцати членов:

.

Заметим, что если заданы первый член и разность арифметической прогрессии, то удобно пользоваться формулой суммы, представленной в другом виде. Подставим в формулу (5) вместо  выражение  получим:  т.е.

 

 (6)

 

Если для решения рассмотренной задачи воспользоваться формулой (6), то вычисления будут выглядеть так:

.

 Геометрическая прогрессия

Рассмотрим последовательность, членами которой являются степени числа 2 с натуральными показателями: 2; ; ; ; … .

Каждый член этой последовательности, начиная со второго, получается умножением предыдущего члена на 2. Эта последовательность является примером геометрической прогрессии.

Определение. Геометрической прогрессией называется последовательность отличных от нуля чисел, в которой каждый член, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.

Иначе говоря, последовательность  - геометрическая прогрессия, если для любого натурального n выполняются условия:

 и , (1)

где q - некоторое число. Обозначим, например, через  последовaтeльность натуральных степеней числа 2. В этом случае для любого натурального n верно равенство ; здесь .

Из определения геометрической прогрессии следует, что отношение любого ее члена, начиная со второго, к предыдущему члену равно q, т.е. при любой натуральном n верно равенство: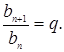

Число q называют знаменателем геометрическойпрогрессии. Очевидно, что знаменатель геометрической прогрессии отличен от нуля.

Чтобы задать геометрическую прогрессию, достаточно указать ее первый член и знаменатель.

Пример 1. Если  и  то получим геометрическую прогрессию:

Пример 2. Условиями  и  задается геометрическая прогрессия - 2; - 6; ; - 54; - 162; ... .

Зная первый член и знаменатель геометрической прогрессии, можно найти последовательно второй, третий, а также любой её член:

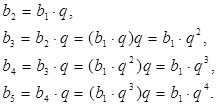
Точно так же находим, что  и т. д. Вообще, чтобы найти  , мы должны умножить на  , т. е.

Мы получили формулу n-го члена геометрической прогрессии.

Выведем теперь формулу суммы n первых членов произвольной геометрической прогрессии. Воспользуемся тем же приемом, с помощью которого была вычислена сумма S.

Пусть дана геометрическая прогрессия . Обозначим сумму n первых ее членов через :

Умножим обе части этого равенства на q:.

Учитывая, что  получим:

 (6)

Вычтем почленно из равенства (6) равенство (5) и приведем подобные члены:

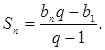Пусть , тогда  (7)

Мы получили формулу суммы n первых членов геометрической прогрессии, в которой . Если , то все члены прогрессии равны первому члену и  [25].

Заметим, что при решении многих задач удобно пользоваться формулой суммы n первых членов геометрической прогрессии, записанной в другом виде. Подставим в формулу (7) вместо bnвыражение  . Получим:

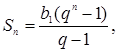 если . (8)

Пример 1. Найдем сумму , слагаемые которой являются последовательными членами геометрической прогрессии 1; x; ; …

Первый член прогрессии равен 1, а знаменатель ранен х. Так как  является членом этой прогрессии с номером n, то задача состоит в нахождении суммы nпервых её членов. Воспользуемся формулой (7):

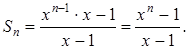
Таким образом,

Умножим левую и правую части последнего равенства на . Получим тождество

В частности, при  и  приходим к известным формулам:

Число  называют суммой бесконечной геометрической прогрессии, у которой .

Это записывают так: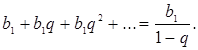

Обозначив сумму прогрессии  буквой S, получим формулу

 

 

 

Заметим, что если , то сумма п первых членов геометрической прогрессии  при неограниченной увеличении п не стремится ни ккакому числу. Бесконечная геометрическая прогрессия имеет сумму только при .

Пример 1. Найдем сумму бесконечной геометрической прогрессии 12; - 4; ; ….

У этой прогрессии  . Значит, условие   выполняется. По формуле (9) получим: .

Пример 2. Дан квадрат, сторона которого равна 4 см. Середины его сторон являются вершинами второго квадрата, середины сторон второго квадрата являются вершинами третьего квадрата и т. д. Найдем сумму площадей всех квадратов.

 

Из геометрических соображений ясно, что площадь каждого следующего квадрата равна половине площади предыдущего. Таким образом, последовательность площадей квадратов является геометрической прогрессией, первый член которой равен 16, а знаменатель равен . Найдем сумму этой геометрической прогрессии:  

Значит, сумма площадей всех квадратов равна 32 см2.

Заметим, что аналогичным образом можно представить в виде обыкновенной дроби любую бесконечную десятичную периодическую дробь [12, с. 267].

 

1.2 Анализ учебно-методической литературы

 

Хорошо известно, что успехи в обучении школьников во многом зависят от содержания и структуры учебника, по которому они занимаются. По одним учебникам школьники работают с удовольствием. Другие учебные тексты воспринимаются иначе; видно, что большинство учеников с неохотой открывают учебник, находят нужный текст и равнодушно начинают работать с ним. Чем же это обусловлено? Попытаемся сравнить известные школьные учебники с позиций подачи темы «Прогрессии» и доступности усвоения учебного материала.

В современной школе наибольшее распространение получили учебники известных ученых и педагогов: Ш. А. Алимов, Ю. М. Колягин; Г. К. Муравин, К. С. Муравин, О. В. Муравина; Ю. Н. Макарычев, Н. Г. Миндюк; А. Г. Мордкович, Н. П. Николаев; Ю. М. Колягин, М. В. Ткачева.

В статьях, посвященных исследованиям учебников по алгебре авторы считают, что некоторые учебники непригодны для современной школы или наоборот, восхищаются новыми подходами автора к изложению школьного курса алгебры.

В учебниках алгебры 9 класс авторов Ю. Н. Макарычев, Н. Г. Миндюк; А. Г. Мордкович, Н. П. Николаев; Ю. М. Колягин, М. В. Ткачева тема «Прогрессии» излагается по традиционной методике [2]

1.                 Ю. Н. Макарычев, Н. Г. Миндюк. 9 класс: Учебник для общеобразовательных учреждений. – М.: Просвещение, 2021.

Глава 4 посвящена прогрессиям, сначала вводится в рассмотрение числовая последовательность, затем арифметическая прогрессия, затем геометрическая прогрессия, для тех, кто хочет знать больше, затем вводится метод математической индукции.

2.                 Мордкович А.Г. Алгебра. 9 кл.: Учебник для общеобразовательных учреждений. – М.: Мнемозина, 2020. -192 с. [11]

Глава 4 посвящена прогрессиям, сначала вводится в рассмотрение числовая последовательность, затем арифметическая прогрессия, затем геометрическая прогрессия, рассматриваются основные результаты, задачный материал обширен, круг рассматриваемых задач полно иллюстрирует теоретическую основу.

3.                 Мордкович А.Г. Алгебра. Углубленное изучение. 9 класс: учебник. – М.: Мнемозина, 2021. – 296 с.

Этот учебник является продолжением аналогичного учебника для 8-го класса. В нем практически полностью реализована действующая государственная программа для классов с углубленным изучением математики в основной школе (включая более сложный и дополнительный материал), книга поможет учителю организовать предпрофильное обучение школьников, которые в старших классах выберут профильную подготовку по математике.

Глава 7 «Прогрессии»: помимо рассматриваемых в основном учебнике тем арифметическая и геометрическая прогрессия, вводится в рассмотрение метод математической индукции [11, с. 215]

В учебниках алгебры 9 класс авторов Ш. А. Алимов, Ю. М. Колягин; Г. К. Муравин, К. С. Муравин, О. В. Муравина темы алгебраической и геометрической прогрессии вводятся параллельно.

1.                 Алгебра. Учебник для 9 класса средней школы / под ред. Ш.А. Алимова. –  М.: Просвещение, 2021.

В данном учебнике тема «Арифметическая и геометрическая прогрессии» изучается в 5 главе «Прогрессии». Тема изучается в последней четверти, после темы «Элементы тригонометрии». В первом параграфе изучается числовая последовательность, определения числовой последовательности не дается. Дается два способа задания последовательности: аналитический и рекуррентный. Далее изучается арифметическая прогрессия: индуктивно дается определение арифметической прогрессии, выводится формула n-ого члена, формулируется свойство арифметической прогрессии, которое вводится через задачу (при доказательстве используется свойство средней линии в трапеции), выводится и доказывается формула суммы n первых членов арифметической прогрессии. Критерий арифметической прогрессии, как в учебниках Мордковича и Виленкина, не формулируется. После арифметической прогрессии изучается геометрическая прогрессия: индуктивно дается ее определение, формула n-ого члена, выводится свойство геометрической прогрессии (критерий также не формулируется), выводится и доказывается формула суммы n первый членов геометрической прогрессии. Бесконечно убывающей геометрической прогрессии посвящен отдельный параграф. Говорится о том, что если n неограниченно возрастает, то qⁿ  стремится к нулю, вводится обозначение этого (сначала это все вводится на конкретной последовательности), дается определение суммы бесконечно убывающей геометрической прогрессии, выводится формула суммы бесконечно убывающей геометрической прогрессии. Таким образом, Алимов вводит некоторые понятия предела последовательности, но самого понятия предела не касается, как, например, Виленкин [1, c. 148]

2.                 Муравин К.С. и др. Алгебра. 9 кл.: Учебник для общеобразовательных учреждений. – М.: Дрофа, 2021. – 240 с.

Учебник завершает учебно-методический комплект по алгебре 7-9 классов. Теоретический материал учебника разбит на обязательный и дополнительный, четко сформулированы алгоритмы решения стандартных задач.дифференцированная система упражнений содержит задания обязательного и повышенного уровня, развивающие задачи и трудные.

Глава 4 носит название «Прогрессии», содержит параграфы: числовые последовательности (последовательность и функции, рекуррентные последовательности), арифметическая и геометрическая прогрессии (определение прогрессии, формулы n-го члена прогрессии), сумма членов прогрессий (сумма первых n членов арифметической и геометрической прогрессии, сумма БУГП). Достаточно большой объем практического материала на отработку теории.

В отличие от других учебников для 9 классов, в которых также представлена тема «Прогрессии», в данном учебнике ведется параллельное рассмотрение арифметической и геометрической прогрессии. Укрупнение дидактических единиц существенно упрощает изложение темы для учителя и способствует лучшему восприятии материала учениками.

 

1.3. Математический аппарат арифметической и геометрической прогрессии

 

В данном подпункте собраны все основные формулы необходимые для вычисления прогрессии, как арифметической, так и геометрической.

Таблица 1.1 - Формулы арифметической прогрессии

Определение (рекур-рентная формула)
Разность
Формула n-го члена
Сумма n первых   членов
Характеристическое свойство

 

Таблица 1.2 - Формулы геометрической прогрессии:

Определение (рекур-рентная формула)
Разность
Формула n-го члена
Сумма n первых   членов (сумма беск. убыв. геометр. прогр.)
Характеристическое свойство

 

 

ГЛАВА 2. МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ ПО ПРИМЕНЕНИЮ ПРАКТИКО- ОРИЕНТИРОВАННЫХ ЗАДАЧ ПО ТЕМЕ «ПРОГРЕССИЯ» НА УРОКАХ МАТЕМАТИКИ

 

2.1 Задачи практической направленности по теме «Прогрессия»

 

Задача 1. Продолжительность прогулки грудного ребёнка в первый день составляет 20 минут, за тем она увеличивается ежедневно на одно и то же время и на 11-ый день   доводится до 2ч. в день. На какое количество времени надо увеличивать продолжительность прогулки ежедневно?

Решение: Имеем арифметическую прогрессию, в которой:

 

 

Длительность прогулки составит 2 часа (номер члена):

 

 

Всего ребенок проведет на улице (сумма первых 11 часов):

 

 

Ответ: на 11 дней; всего 770 минут.

Задача 2. Премиальный фонд составляет 16250р.

Надо разделить его между четырьмя сотрудниками, согласно доле участия, каждого так, чтобы каждый следующий получил в 1,5 раза больше предыдущего. Какую премию получит каждый сотрудник?

Пусть первый сотрудник получит премию x.

Второй получит

Третий

Четвертый

Получим следующее уравнение:

 

 

Значит первый сотрудник получит 2000.

Второй получит:

Третий получит: 

Четвертый получит:

Ответ: 2000; 3000; 4500; 6750.

Задача 3. Каждое простейшее одноклеточное животное инфузория-туфелька размножается делением на 2 части. Сколько инфузорий было первоначально, если после шестикратного деления их стало 1280?

Решение. Шестикратное деление, означает, что каждый раз (из шести) их число удваивалось и увеличилось в   раза. Следовательно, изначально животных было:

Задача 4: Планируя выпуск нового электронного прибора, экономисты предприятия определили, что в первый месяц (а это февраль) может быть изготовлено 200 приборов; далее предполагалось увеличивать ежемесячно на 20 изделий. Сколько приборов изготовит предприятие в 3 квартале?

Решение: 3 квартал – это месяцы: июль, август, сентябрь.

В июле будет выпущено(дет.), тогда в августе – 320 дет., в сентябре – 340 дет. За три месяца, т.е. в 3 квартале, будет выпущено (деталей).

Задача 5: Углы треугольника образуют арифметическую прогрессию. Тупой угол равен 100º. Найдите все углы треугольника.

Решение. Пусть углы треугольника:  , в порядке возрастания их градусной меры. Поскольку тупой угол в треугольнике может быть только один, то он наибольший, т.е. , при этом  где d – разность прогрессии.

Сумма углов треугольника 180º, следовательно

 Тогда  

Ответ: 20º, 60º, 100º.

 

2.2 Методические рекомендации по применению составленных задач на уроках математики 9 класса

 

Существует несколько подходов к изучению прогрессий. По традиционной методике арифметическая и геометрическая прогрессия рассматриваются на уроках раздельно. В заключении же проводится отдельное обобщающее занятие, позволяющее систематизировать полученные знания. В подобной ситуации изучение темы прогрессий проходит поэтапно — от простого к сложному, от знакомства к анализу.

Методической особенностью изучения темы является одновременное изучение двух разнотипных прогрессий. В таком случае материал подается с точки зрения сравнения — поиска аналогии и различий. Это максимально включает в работу логическое мышление. При одновременном изучении предлагается следующее тематическое планирование уроков.

Это позволяет учащимся рассмотреть тему с разных ракурсов, а значит, в конечном итоге прояснить ее суть.

В результате изучения темы учащийся должен освоить:

Учебные задачи темы:

1                    Формирование представления о числовых последовательностях, о рекуррентном способе задания числовых последовательностей.

2                    Формирование представления об арифметической и геометрической прогрессиях как частных случаях числовых последовательностей; изучение их определений и свойств (по аналогии друг с другом).

3                    Раскрытие практического значения этих понятий (особенно бесконечно убывающей геометрической прогрессии).

4                    Выявление групп взаимосвязанных задач по теме.

В результате изучения темы ученик:

- знает: понятие числовой последовательности; понятие бесконечной числовой последовательности; понятие членов последовательности; два способа задания последовательности (с помощью формулы ее n-ого члена и рекуррентный способ); определение арифметической прогрессии, определение геометрической прогрессии; рекуррентную формулу n-ого члена арифметической прогрессии, рекуррентную формулу n-ого члена геометрической прогрессии; характеристическое свойство арифметической прогрессии и его доказательство; характеристическое свойство геометрической прогрессии и его доказательство; формулу n-ого члена арифметической прогрессии, формулу n-ого члена геометрической прогрессии; формулу суммы n первых членов арифметической прогрессии и ее доказательство, формулу суммы n первых членов геометрической прогрессии и ее доказательство; определение бесконечно убывающей геометрической прогрессии; определение суммы бесконечно убывающей геометрической прогрессии;  формулу суммы бесконечно убывающей геометрической прогрессии.

- умеет: формулировать определение рекуррентного способа задания последовательности; формулировать определение арифметической прогрессии, формулировать определение геометрической прогрессии; применять рекуррентную формулу n-ого члена арифметической прогрессии, применять рекуррентную формулу n-ого члена геометрической прогрессии; формулировать, доказывать и применять характеристическое свойство арифметической прогрессии, формулировать, доказывать  и применять характеристическое свойство геометрической прогрессии; применять формулу n-ого члена арифметической прогрессии, применять формулу n-ого члена геометрической прогрессии; доказывать и применять формулу суммы n первых членов арифметической прогрессии, доказывать и применять формулу суммы n первых членов геометрической прогрессии; формулировать определение бесконечно убывающей геометрической прогрессии; формулировать определение  суммы бесконечно убывающей геометрической прогрессии; применять формулу суммы бесконечно убывающей геометрической прогрессии.

- понимает: что арифметическая и геометрическая прогрессии являются числовыми последовательностями; взаимосвязь понятий арифметической прогрессии и среднего арифметического, взаимосвязь понятий геометрической прогрессии и среднего геометрического; аналогию определений и свойств арифметической и геометрической прогрессий; что характеристическое свойство арифметической прогрессии является критерием (свойством и признаком), что характеристическое свойство геометрической прогрессии является критерием (свойством и признаком);как были получены формулы n-ого члена арифметической и геометрической прогрессии; практическое значение арифметической, геометрической прогрессий (в особенности бесконечно убывающей геометрической прогрессии).

В таком случае параллельно рассматриваются только ключевые понятия: что такое геометрическая и арифметическая прогрессия как находится ее n-ый член. После этого ознакомление с этими двумя числовыми рядами проходит раздельно и последовательно. В результате школьники приобретают важные навыки: сопоставление понятий; нахождение схожести и различия; определение закономерностей; создание математических моделей и т.п. Усвоение учебного материала при указанном подходе максимальное, а также активно развивается логика, зрительная память, грамотная с точки зрения математики речь.

Это позволяет учащимся рассмотреть тему с разных ракурсов, а значит, в конечном итоге прояснить ее суть.

На первом уроке темы необходимо разъяснить смысл понятий последовательность, п-й член последовательности, выработать умение использовать индексные обозначения.

Для более сильных учащихся можно ввести строгое определение последовательности как функции натурального аргумента, понятие области определения и области значений такой функции, графическое изображение последовательности. На этом же уроке уместно показать различные способы задания последовательности.

Необходимым условием приобретения умений решать задачи и примеры с прогрессиями является знание всех формул из этой темы и наличие навыков их преобразования. Поэтому на практике необходимо уделять особое внимание приемам, позволяющим повышать эффективность усвоения учащимися формул и выражать из них неизвестные величины.

Рассмотрим некоторые формы отработки знаний формул темы «Прогрессии», позволяющие активизировать познавательную деятельность учащихся и были использованы в данном классе.

1. Дидактическая карточка «Эстафета формул»

При изучении нескольких формул темы «Прогрессии» целесообразно применение дидактических карточек «Эстафета формул». На листе бумаги в столбик записаны формулы, в которых вместо какой-либо величины вырезан круг. Карточку удобно оформлять в виде перфокарты со сменной бумажной полоской-подложкой. Заполняется карточка так: вписывая в первую формулу недостающую величину, её же записывают во вторую формулу, туда, куда показывает стрелка. Процедура продолжается, пока не будут заполнены все пропуски.

Правильность заполнения карточки проверяется с помощью заготовленной подложки-ключа. Достоинств у дидактических карточек «Эстафеты формул» несколько. Во-первых, это нетрадиционный способ работы с формулами, что, несомненно, привлекает внимание учащихся. Во-вторых, формы работы с карточками «Эстафета формул» могут быть разнообразны. Возможно заполнение карточки одним учеником, при этом проверяется знание им формул данной темы. Приемлема организация групповой работы, когда учащиеся поочередно записывают пропущенные величины в формулы, связанные в общую цепочку. В этом случае у учащихся возникает чувство ответственности перед товарищами за выполнение своего задания, потому что от правильности записи одной формулы зависит верность заполнения дальнейших пропусков. В-третьих, проверка выполнения заданий очень проста и оперативна, поэтому она может быть осуществлена даже учащимися.

2. «Математическая электровикторина»

Отработка знания формул и умения работать с ними может быть осуществлена с помощью математической электровикторины.

Электровикторина представляет собой коробку, внутри которой собрана электрическая схема. Передняя панель имеет ряды гнезд, съёмные карточки с формулами, изучаемыми в теме «Арифметическая и геометрическая прогрессии»; справа расположена лампочка, соединённая внутри коробки с гальваническим элементом. От этой цепи лампочка- гальванический элемент отходят длинные мягкие провода, оканчивающиеся металлическими контактами. Слева на карточках расположены вопросы, справа в беспорядке, но в соответствии со схемой, - ответы на них.

Работа с математической электровикториной обычно организуется в парах. При этом учащиеся выполняют задания и контролируют правильность выполнения. Правила следующие: учащийся вставляет один штырь в левое гнездо, читает вопрос, ищет справа ответ и вставляет в его гнездо второй штырь от провода. Если ответ выбран правильно, то лампочка загорится. Другой ученик по количеству верных ответов выставляет оценку отвечающему. Затем ребята меняются ролями.

Умение решать математические задачи является наиболее яркой характеристикой состояния математического мышления учащихся, уровня их математического образования.

Понятие прогрессии следует закрепить, решая задачи различных видов.

1. Используя формулы общих членов прогрессий и суммы первых членов прогрессий, а также суммы бесконечной убывающей по модулю геометрической прогрессии, находят один из компонентов этих формул, если остальные известны.

2. Задачи, в которых по заданной зависимости между членами арифметической и геометрической прогрессий (или одной из них), требуется найти сами прогрессии.

3. Задачи с практическим и экономическим содержанием на прогрессии.

4. Нестандартные задачи на прогрессии.

Уроки повторения, обобщения и систематизации знаний по теме «Арифметическая и геометрическая прогрессии» требуют четкого логического мышления, строятся на более высоком его уровне. Оно сложнее и труднее для учеников, но полезнее для их развития. Такие уроки доставляют интеллектуальное удовлетворение учащимся, так как они проверяют здесь свои способности; чувствуют, что уроки повторения, обобщения и систематизации знаний развивают их ум.

Целью уроков повторения, обобщения и систематизации знаний по теме «Арифметическая и геометрическая прогрессии» является восстановление, закрепление и систематизация накопленных учениками знаний.

Примерная структура стандартных таких уроков имеет следующий вид.

1. Проверка домашнего задания.

2. Ознакомление учеников с планом повторения, записанным на доске.

3. Повторение по намеченному плану.

4. Постановка домашнего задания.

5. В конце урока, после просмотра всех вычислений, выполненных на уроке, повторяются определения, формулы и свойства, изученные в теме «Арифметическая и геометрическая прогрессии».

Итак, уроки повторения, обобщения и систематизации знаний призваны подготовить учащихся к контрольной работе по теме «Арифметическая и геометрическая прогрессии». В этом заключается их значимость в процессе обучения.

Проверка знаний, умений и навыков, учащихся является важным процессом, определяющим результативность и эффективность обучения. Она имеет не только обучающее, но и воспитательное значение.

Целями проверки являются диагностика и коррекция знаний; учет результативности отдельного этапа процесса обучения; определение итоговых результатов обучения.

Обратимся к вопросу об активизации познавательной деятельности учащихся при выполнении самостоятельных работ по математике. Эффективность процесса обучения математике определяется многими факторами. Важную роль при этом играет активная позиция каждого из учащихся. Практика показала, что опытные учителя уделяют первостепенное внимание воспитанию такой позиции.

Одним из признаков активности школьников является их положительное отношение, их интерес к предмету, к изучаемому материалу, к содержанию заданий, к способам выполнения.

Учитывая особенности стимуляции познавательных интересов учащихся при помощи содержания учебного материала по теме «Арифметическая и геометрическая прогрессии» к индивидуальным самостоятельным работам, способствующим формированию познавательного интереса к этому материалу, можно отнести следующие задания:

1. Задания, содержание которых показывает роль прогрессий, их свойств в практической, технической, экономической деятельности людей.

2. Задания, которые показывают связь математики с другими учебными предметами.

3. Задания на обновление усвоенных ранее знаний.

4. Задания, содержащие элементы занимательности.

5. Задания, содержащие исторический материал.

Такие задания можно использовать в качестве индивидуальных самостоятельных работ для учащихся с целью привлечь их к занятиям математикой и, в частности, к изучению прогрессий.

Большое значение в практике обучения математике играют так называемые управляемые самостоятельные работы, позволяющие ученикам осуществлять самоконтроль в процессе их выполнения, а значит, активизировать мыслительную деятельность учащихся. В таких работах задания составляются так, чтобы ответ предыдущего задания включался в следующее за ним. К таким заданиям предлагается список ответов для самоконтроля.

 

 

 

 

 

ЗАКЛЮЧЕНИЕ

 

В результате проведения работы была достигнута основная цель: выявление методических особенностей при изучении темы: «Прогрессии» в школьном курсе математики и, тем самым, были решены все поставленные задачи, а именно

¾               анализ учебно-методической литературы по проблеме исследования помог выделить методические особенности темы «Прогрессии» в школьном курсе алгебры 9 класса;

¾               выделение методических особенностей определило метод параллельного изучение тем «Алгебраическая прогрессия» и «Геометрическая прогрессия»;

¾               При решении задач, поставленных перед нами в итоговой работе, были разработаны планы – конспекты уроков по теме исследования, которые можно предложить учителям школы.

Основные дидактические единицы темы: понятие числовой последовательности, определения понятий арифметической и геометрической прогрессий, формулы n-го члена арифметической и геометрической прогрессий, свойства арифметической прогрессии о среднем арифметическом и геометрической прогрессии о среднем геометрическом, формулы суммы n первых членов арифметической и геометрической прогрессий, определение понятия бесконечно убывающей геометрической прогрессии, формула суммы бесконечно убывающей геометрической прогрессии.

Для арифметической и геометрической прогрессий аналогично выводятся формулы n-ого члена методом неполной индукции, в которых n-ый член находится через первый член и разность для арифметической / знаменатель для геометрической прогрессии. Эти формулы являются ещё одним способом задания прогрессии. Вообще в математике эти формулы можно доказать с помощью метода математической индукции, но он достаточно сложен для восприятия школьников, поэтому данные формулы приведены в рассматриваемом учебнике без доказательства.

Также задачи, приведенные в данной теме с решением в тексте параграфов, являются аналогичными. Правила решения подобных задач не сформулированы. Учитель может их выделить совместно с учениками (чтобы найти требуемое в задаче, можно выписать соответствующую формулу, определить, что в ней известно, а что нет, затем выразить из этой формулы то, что нужно найти, подставив известные значения).

Так как прослеживается явная аналогия между понятиями прогрессий, то следует пере структурировать тему так, чтобы соответствующие дидактические единицы изучались совместно.

Таким образом, цель достигнута. Его результаты подтвердили выдвинутую гипотезу, что параллельное изучение темы «Прогрессии» позволит добиться увеличение коэффициента усвояемости обучающихся.

 

 

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

 

1.                 Алгебра [Текст]: Учеб. для 9 кл. общеобразоват. учреждений / Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др.; под ред. Ш.А. Алимова. – М.: Просвещение, 2021.– 384 с.: ил.

2.                 Алгебра [Текст]: Учеб. для 9 кл. общеобразоват. учреждений / А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын и др.; под ред. А.Н. Колмогорова. – М.: Просвещение, 2021.– 384 с.: ил.

3.                 Алгебра 9 кл. [Текст]: Учеб. для общеобразоват. учреждений. / А.Г. Мордкович, И.М. Смирнова, Л.О. Денищева и др.; под ред. А.Г. Мордковича. – М.: Мнемозина, 2021.– 375 с.: ил.

4.                 Алгебра [Текст]: Учеб. для 9 кл. общеобразоват. учреждений: базовый и профильный уровни / С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин.– М.: Просвещение, 2021.– 383 с.: ил.

5.                 Бродских И.Л. Сборник текстовых задач по математике для профильных классов: 7-11 кл. [Текст] / И.Л. Бродских, А.М. Видус, А.Б. Коротаев. – М.: АРКТИ, 2018.– 310 с.

6.                 Виленкин Н.Я. Алгебра 9 кл. [Текст] : Учеб. пособие для шк. и кл. с углубл. изуч. математики / Н.Я. Виленкин, О.С. Ивашев-Мусатов, С.И. Шварцбурд.– М.: Мнемозина, 2016.– 335 с.

7.                 Епишева О.Б. Технология обучения математике на основе деятельностного подхода [Текст]: Кн. для учителя. / О.Б. Епишева. – М.: Просвещение, 2017.– 223 с.

8.                 Колягин Ю.М. Русская школа и математическое образование: Наша гордость и наша боль [Текст] / Ю.М. Колягин. – М.: Просвещение, 2019.– 318 с.

9.                 Кузнецова Г.М. Программа для общеобразовательных школ, гимназий, лицеев. Математика 5-11 кл. / Г.М. Кузнецова, Н.М. Миндюк.– М.: Дрофа, 2018.– 172 с.

10.             Математика: 5-11 кл.: Программы. Тематическое планирование [Текст]: для общеобразоват. шк., гимназий и лицеев / М-во образования РФ; Сост. Г.М. Кузнецова, Н.Г. Миндяк. – М.: Дрофа, 2018.– 320 с.

11.             Мордкович А.Г. Алгебра. 9 кл. [Текст]: Учеб. для общеобразоват. учреждений (профильный уровень) / А.Г. Мордкович, П.В. Семенов. – М.: Мнемозина, 2020.– 287 с.: ил.

12.             Обухова Л.А. Поурочные разработки по алгебре: 9 класс. [Текст] / Л.А. Обухова, О.В. Занина, И.Н. Данкова. – М.: ВАКО, 2018.– 304 с

13.             Саранцев Г.И. Методика обучения математики в средней школе [Текст]: Учеб. пособие для студ. мат. спец. пед. вузов и универ-тов. / Г.И. Саранцев. – М.: Просвещение, 2018.– 296 с.

14.             Сборник нормативных документов. Математика: (Концепция профильного обучения на старшей ступени общего образования. Приложение к приказу Минобразования России от 18.07.2002, Москва. № 2783) [Текст] / Сост. Э.Д. Днепров, А.Г. Аркадьев. – 2-е изд., стереотип. – М.: Дрофа, 2016.– 80 с.

15.             Стандарт среднего (полного) общего образования по математике. Профильный уровень: (Федеральный компонент государственного стандарта) [Текст] / Э.Д. Днепров, А.Г. Аркадьев. – М.: Дрофа, 2016.– С. 81-91.

16.             Фридман Л.М. Психология детей и подростков [Текст]: Справочник для учителей и воспитателей. / Л.М. Фридман. – М.: изд-во ин-та психотерапии, 2019.– 198 с.

17.             Фридман Л.М. Теоретические основы методики обучения математики [Текст]/ Л.М. Фридман. – М.: Едиториал УРСС, 2017.– 248 с.

 

Скачано с www.znanio.ru