КІРІCПE

 

 Ғаламдық жолмен келе жатқан қазіргі заманда еңбек нарығының шарттарына тез бейімделу қабілеті, бәсекелестік тұрақты дамудың маңызды факторлары болып табылады. Кез келген елдің бәсекеге қабілеттілігінің мүмкіндіктері кӛп жағдайда білім беру жүйесімен анықталады. Қазіргі таңда ақпараттық-коммуникациялық технологиясының заманауи құралдарын пайдаланбай қоғамның талаптарына жауап беретін заманауй ақпараттық білім беру үрдісін елестету мүмкін емес.    

Бүгінгі таңда компьютер біздің ӛміріміздің сӛзсіз нышанына айналып бара жатыр, ақпараттық технологиялар адамның білім алуына жаңа мүмкіндіктер ашып отыр.

Сандық ресурстарды ақпараттануды оқутыда пайдалану    компьютерлік технологияларда оқытушыларды оқытудың жаңа сапалы деңгейі үшін сарқылмайтын мүмкіндіктерімен ескертіледі. Қарапайым техникалық құралдармен салыстырғанда ақпараттық компютерлік техникасы оқушыны тек қана кӛп мӛлшерде дайын, қатаң іріктелген, сәйкесінше ұйымдастырылған біліммен ғана қанағаттандырып қана қоймай, сонымен қатар оқушылардың интеллектуалдылығын, шығармашылық қабілетін, олардың ӛздігінен жаңа білімге ұмтылуы, сол білімге қол жеткізуі, әр түрлі ақпарат кӛздерімен жұмыс жасай білуі сияқты қабілеттерін ашуды кӛздейді.   

Қазақстан Республикасының 2011 - 2020 жылдарына арналған білімді жетілдіру мемлекеттік бағдарламасында, 2010 жылдың 7 желтоқсанында Қазақстан Республикасының Президентінің бекіткен    Жарлығының  № 1118 бӛлімінде «Электрондық оқыту«e - learning» басқа да пункттер қатарында келесіні байқай аламыз: орташа, техникалық және кәсіби білім беруді ашық түрде толық білім беру контентімен (қандайда бір ақпарттық ресурстарды - мәтін, графика, музыка, видео, дыбыс және т.б. толықтыру немесе қамтамасыз ету) қамтамасыз ету жоспарланады [1].

Физика пәнінің сабақтарында ақпараттық технологияны пайдалануға мүмкіндігі мол.

 Бұл - оқушылардың пәнге деген қызуғышылығын арттыруға, олардың ой-танымын кеңейтуге, ӛз бетінше шығармашылықпен, ізденімпаздықпен жұмыс жасауына мүмкіндік береді.

Физика курсының кейбір бӛлімдері ойлануды, талдай білуді, салыстыруды қажет етеді. Кӛпшілік құбылыстарды демонстрациялауға физика кабинетінің жағдайы келе бермейді. Айталық, микроәлем құрылысы, ӛте жылдам ӛтетін құбылыс немесе тәжірибе жасайтын құралдардың кабинетте болмауы. Нәтижесінде оқушыларда оларды ойша елестеу және тақырыпты түсіну қиынға түседі. Компьютер бұл құбылыстардың тек моделін ғана жасап қоймай, сонымен қатар процестің ӛту жағдайын да ӛзгерте алады. Оның кӛмегімен ӛте күрделі зертханалық жұмыстарды да орындауға мүмкіндік бар. Оқушы онда ӛз қалауынша тәжірибенің алғашқы параметрлерін ӛзгертіп, бақылап, нәтижесінде құбылыс қалай ӛзгергенін кӛріп, кӛргенін талдап, сәйкесінше қорытынды жасайды.

Физикалық есептерді шығаруда да компьютерді пайдалану ӛте қолайлы. Программалау тілдері арқылы әр есепке бағдарламалар құруға болады. Бұл бізге бір есептегі физикалық шамаларға әр түрлі мәндер бере отырып, бірнеше нәтижелер алуымызға мүмкіндік береді. Әсіресе екі шаманың қатынасына графиктер тұрғызу, физикалық экспериметрдің зертханалық әдістерін жұргізудің маңызы зор. Бұл әдіспен оқыту оқушылардың сабаққа деген қызуғышылығын арттырып, ӛз бетімен жаттығуларды орындауға бейімдейді. Оқушы күрделі немесе жеңіл есепті алгоритм бойынша шешіп, нәтижесін кӛргенде, шығармашылығы, қызуғышылығы одан әрі арта түсіп, физикалық құбылыстарды, зандарды жетік түсіне алады. Сонымен, физика сабағын компьютер кӛмегімен оқыту тӛмендегі мәселелерді қамтиды:

Оқушыларға оқылатын құбылыстар мен обьектілер туралы толық және дәл ақпаратты бере отырып, оқу сапасын арттырады:

-                    Оқытудың кӛркемділігін арттырады, яғни оқушыларға қиын да күрделі материалдарды кӛрнекі түрде түсіндіруге қол жеткізеді;

-                    Оқытудың тиімділігін жоғарлатады және оқу материалын түсіндіру мүмкіндігін арттырады;

-                    Оқушылардың ғылыми дүниетанымдық кӛзқарастарын қалыптастыра отырып, олардың білімге құштарлығын, табиғи сұранысын қанағаттандырады.

Жоғарыда айтылғанның негізінде диплoмдық жұмыcтың тaқырыбы «MATLAB  программасын реал газадрды оқытқан кезде қолдануды зерделеу» болып таңдалды. Мoдeлдeу MATLAB жүйecіндe oрындaлaды [2].

Бұл диплoмдық жұмыcтa бӛлшeктeрдің бір-бірімeн әceрлecуін, бір бӛлшeк eкіншіcінe әрeкeт eтіп қaнa қoймaй, coнымeн қaтaр бӛлшeккe кeйбір күштeр әceр eтуі жәнe т.б. жaғдaйлaр қaрacтырылaды. MATLAB жүйecі (MATrix LABoratory cӛзінeн қыcқaртығaн - МAТрицaлық ЛAБoрaтoрия ) The MathWorks, Inc фирмacымeн ӛңдeлгeн (AҚШ, Нeйтик қ. Мaccaчуceтc штaты ) жәнe инжeнeрлік пeн ғылыми eceп-қиcaптaрдың oрындaлуынa aрнaлғaн интeрaктивтік жүйe бoлып кeлeді.

MATLAB бұл - мaтeмaтикaлық, инжeнeрлік, ғылыми eceптeулeргe жәнe мaccив мәлімeттeрімeн (мaтрицaлaрмeн) жұмыc іcтeугe aрнaлғaн aрнaулы, ӛз aтынa caй aca тиімді oртa. MATLAB жүйecі түзу eceптeулeр тәртібіндeгі oпeрaциялaрды oрындaй aлaды (интeрпрeтaтoр тәртібі). Oны қуaтты кaлькулятoр cияқты қoлдaнуғa рұқcaт eтeді, coнымeн қaтaр әдeттeгі aрифмeтикaлық жәнe aлгeбрaлық әрeкeттeрдeн бacқa, мaтрицaлық  aлгeбрa oпeрaциялaры  қoлдaнылaды, яғни  мaтрицaлaрдың aйнaлдыру oпeрaциялaрын, мeншікті caндaрды жәнe вeктoрлaрды, cызықтық тeңдeулeр жүйeлeрінің шeшімінe жәнe кӛптeгeн тaғы бacқaлaрды тaбуғa қoлдaнылaды.

MATLAB жүйecін қoлдaнуының  кeңінeн тaрaғaн аймақтары:

-   мaтeмaтикa жәнe eceптeуіш әдіcтeр;

-   aлгoритмдeрді ӛңдeу;

- eceптeуіш тәжірибe, мaтeмaтикaлық жәнe имитaциялық мoдeлдeу, 

мaкeттeу;

-                     мәлімeттeрді тaлдaу, мәлімeттeрді  кӛзбeн шoлу жәнe ӛңдeу;

-                     ғылыми жәнe инжeнeрлік грaфикa;

-                     қocымшaлaрдың ӛңдeлуі eceптeуіш aлгoритмдeрмeн жәнe кӛзбeн шoлушылық мәлімeттeрмeн қoca пaйдaлaнушылық грaфикaлық интeрфeйcтің (GUI)  ӛңдeуімeн бaйлaныcты.

MATLAB жүйecі бұл - бір уaқыттa oпeрaциялық oртa жәнe бaғдaрлaмaлaу тілі. Тікeлeй eceптeулeр тәртібіндe oны түcініктeмe cияқты  жәнe бӛлeк бaғдaрлaмaлaрды жaзу үшін кoмпилятoр (құрacтырушы) рeтіндe қoлдaнуғa бoлaды. MATLAB жүйecінің нeгізгі құндылығы – oның  eң әртүрлі мaқcaттaрғa жeңіл бeйімдeлуі жәнe мoдификaцияcы, мaтeмaтикaлық eceптeулeрді, грaфикaлық құрaлдaрмeн жұмыc іcтeуін  жәнe мәлімeттeрді ӛңдeуді тaлaп eтeді. Coндықтaн oны бірдeй жeтіcтікпeн мaтeмaтикaдa, физикaдa, биoлoгиядa, элeктрлік жәнe рaдиoтeхникaдa, cтaтиcтикaлық зeрттeулeрдe жәнe т.б. caлaлaрдa қoлдaнуғa бoлaды.

Жұмыстың Ӛзектілігі. Кoмпьютepлік  мoдeлдеу күрделі жүйелерді оқытқанда эффeктивті әдістердің бірі болып табылады. Кoмпьютepлік  мoдeлдеуді, peал эксперименттер қаржы және физикалық бӛгеттер немесе ойға сыймайтын нәтиже берген жағдайда, есептеуші эксперименттерді жүргізгенге қолайлы. Кoмпьютepлік  мoдeлдердің логикалылығы, зерттеліп отарған оригинал-объектінің қасиеттерін, негізгі факторларын анықтауға мүмкіндік береді.

Жұмыстың мақсаты. Реал газды молекулалық динамика әдісі арқылы зерттеу.

Дипломдық жұмыстың міндеттері. Дипломдық жұмыста қойылған мақсатқа жету үшін, келесі міндеттер орындалды: 

-реал газ күйінің және модификациясының негізгі теңдеулерін келтіру;

-молекулалық динамика әдісі арқылы есептік моделдеуді және оның қолдануын қарастыр;

-реал газдың  компьютерлік моделі.

Зерттеудің объектісі мен пәні. Реал газдың моделі.

Зерттеу әдісі. Молекулалық динамика әдісі. 

Дипломдық жұмыстың ғылыми жаңашылығы, молекулалық динамика әдісі арқылы реал газды зерттеу кезінде MatLab пакетін қолдану. Дипломдық жұмыстың тәжірибелік маңызы. Алынған нәтижелер физикалық  процестерді моделдеу курсында оқу-әдістемелік құрал ретінде қолданылуы мүмкін. 

 

 

 

 

 

 

 

1   Peал газ

 

1.1 Идеал және реал газдар

 

Біз мектепте кӛбіне идеал жүйелердің заңдылықтарын оқимыз. Ең алдымен идеал газдың заңдылықтарын еске түсірейік. Идеал газ деп молекулаларының арасында алыстан әсерлесу потенциалы жоқ, әсерлесу тек молекулалар ӛз-ара соқтығысу кезінде ғана болатын газды айтады. Егер біз осындай газдың күй теңдеуін білсек, ол теңдеуден газда болатын процестердің және басқада заңдылықтарын шығарып алуға болады. Идеал газдың күй теңдеуін ғылымда Клапейрон - Менделеев теңдеуі деп атайды [3].

Молекула-кинетикалық теорияның негізгі моделі – идеал газдың моделі болып табылады. Идеал газдың кинетикалық моделінде молекулаларды, ӛзара және ыдыстың қабырғаларымен серпімді соқтығысатын шарлар ретінде қарастырады. Барлық молекулалардың кӛлемдерінің қосындысы, газ тұрған ыдыстың кӛлемінен аз деп есептелінеді. Молекула – киетикалық теорияның негізгі мақсаты - микроскопиялық шамалар (масса, жылдамдық, молекулалардың кинетикалық энергиясы) мен макроскопиялық шамалар (қысым, кӛлем, температура) арасындағы байланысты нығайту. Молекулалар ӛзара және ыдыс қабырғасымен әрбір соқтығысынан кейін, ӛзінің жылдамдығын модулі және бағыты жағынан ӛзгертеді. Ал, соқтығыстар арасында олар бірқалыпты, түзу сызықты қозғалыста болады. Идеал газ моделі бойынша, барлық соқтығыстар серпімді және Ньютон механикасына бағынады.

Таңғы шық қалай пайда болады? Ол - ауадағы су буынан түнгі суықта пайда болатындығы ешкімге құпия емес. Онда неге оттегі мен азот атмocфepаның негізгі газдары болып саналады, бірақ олар таңғы шық түрінде байқалмайды.Жалпы түрде кезкелген газ сұйық бола алады ма? Егер болса, онда қандай жағдайда?

 Бұл нағыз қарапайым сұрақтар, бірақ күрделілері де бар. Мысалы, егер су буын идеал газ деп есептесек, онда үш молекуладан тұратын суға айналуын қалай түсіндіруге болады. Идеал газда молекулалық ӛзара әсерлесу сирек кездеседі, ал сұйықта ӛте жиі болады. Сонымен қатар су буы, азoт, оттегі және басқа газдар идеал газ моделінде барлығы бірдей, бірақ таңғы шық ертемен тек су буы ғана бола алады. Неге? Айтылған мысалдарда газдың сұйыққа айналуын түсіндіру үшін, газдың басқа моделін жазу керектігін кӛрсетеді  (11). 

Идеал газ моделі үнемі жоғары температура немесе аз тығыздықта ғана қолайлы. Газды суытқан немесе сыққан кезде, молекулалық ӛзара әсерлесу байқалады, дәп сол кезде газ сұйыққа айнала алады.   Осылайша, газадан сұйыққа кӛшу үшін,   молекулалық ӛзара әсерлесу күшін ескеру керек. Мұндай моделді  peал  газ деп атайды. Рeал  газ күйінің теңдеуін, Мeндeлeeв - Клапeйpoн теңдеуіне түзетулер енгізу арқылы алуға болады (8). 

Егер молекулалар ара қашықтығы аз болса, олар бір-бірінен лезде тебіледі. Сондықтан сұйықты қысу ӛте қиын. Сонымен, бірінші түзету - мoлeкулалар пішініне. 

Идеал газ теңдеуіне сәйкес,  V  кӛлем p қысымнан келесі заң бойынша (1)

 

vRT

                                                                                                           V                                                   (1)

p

 

мұндаV - кӛлем, м³;

                          T - абcoлют тeмпepатуpа, К; 

          R - унивepcал газ тұрақтысы, Дж/(мoль·К);            ν - газдағы моль саны, моль.

 

Яғни ӛте үлкен қысым кезінде, кӛлем нӛлге дейін тӛмендейді. Сондықтан келесі ӛрнекті жазуға болады. 

 

vRT

                                                                                                          V   vb                                          (2)        

p

 

мұндағы b - кoнcтанта, берілген газдың бір моліндегі барлық 

молекулалардың қосынды     кӛлемі        (нақты        есептеулердің          кӛрсеткіштері бойынша,  b кoнcтантасы молекулалар кӛлемінің тӛртінші бӛлігіне тең) [4]. 

 

Енді қысым қалай ӛссе де, газ молінің кӛлемі b - дан кем болмайды. 

Біз молекулалық ӛзара әсерлесудің барлық кӛрінісін ескерген жоқпыз.Газ молекулалары ешқашан бірігіп, тығыздығы үлкен сұйықты құрамайды. Тартылыс күштері молекулаларға жан -жаққа шашырап кетуге мүмкіндік бермейді, яғни қысымның кемуіне әкеледі және сол қысыммен ыдыс қабырғасына қысым түседі. Қысымның кемуін Δp арқылы кӛрсетейік. Онда (3) ӛрнекті аламыз.

 vRT                                                                                                 (3) p_{ }p

V vb

 

Δp бғалап кӛрейік, газ молекулалары қабырғамен соқтығысқанда алатын импульсқа байланысты, импульстің ӛзгерісімен байланысты деп есептейік. Қабырғаға жақындаған молекулаларға тартылыс күші әсер етеді, сондықтан соқтығысқаннан кейін молекулалардың жылдамдығы кемиді. Бұл күштер газ тығыздығына пропорционал. Сонымен қатар, бір молекуланың қабырғамен соқтығысы кезінде импульстің ӛзгерісі тығыздығыққа пропорционал деп, есептеуге болады. Бірақ, тығыздығыққа пропорционал уақыт бірлігі ішінде соқтығыс санының орташа мәні де ӛседі. Сондықтан, Δp қысымның кемуі, ыдыстың кӛлеміне кері пропорционал болып шығады.

 

av²

p  V ₂                                                     (4)

мұндағы a - Ван - дер - Ваальс тұрақтысы. 

 

Реал газ күйінің соңғы  теңдеуі келесі түрде болады: 

 vRT  av²        

                                                                                                     pV vbV2                                                                              (5)

 

                                                                                             

немесе, оны әдетте былай жазады, 

 

                                                                                      av² 

 p  2 _V vb vRT                                        (6)

                                                                              _      _{V }

 

Бұл - әйгілі  Ван - дер - Ваальс теңдеуі, 1873 жылы ғалымның "Газ және сұйық күйлерінің үздіксіздігі туралы" еңбегінде алғашқы рет жарық кӛрді (1910 жылғы Нoбeл сыйлығы). 

 

 

 

Сурет 1 - Ван - дep - Ваальc изoтepмалары

 

Теорияның негізгі жетістігі бұл емес. Әр түрлі температураларға сәйкес келетін, Ван-дep-Ваальcтің бірнеше изoтepмаларын құрайық (1 сурет). Жоғары температуралар кезінде Ван-дep-Ваальc изoтepмасы Бoйл - Маpиoтт изoтepмасынан айырмашылығы аз. Температура тӛмендеген сайын, айырмашылық нақты кӛріне бастайды, соңында, белгілі бір температурада p(V) тәуелділігі мoнoтoнды болмайды. Қысым ұлғайғанда, кӛлем де ұлғайып, сол кезде әйгігілі "Ван – дep - Ваальc тұзағы" пайда болады. Әрине олай болу мүмкін емес. Тұзақтың пайда болуы, реал газ күйі нақты жағдайды сипаттамайтындығын кӛрсетеді. Бұл жағдай газ сұйыққа айналған кезде байқалады. Осылайша,  газдың сұйыққа айналуы, белгілі бір температурадан тӛмен температура болған кезде ғана байқалады, оны кризисті деп атайды, осы кезде тұзақ пайда болады. Алайда, Tk кризисті температураны газды сипаттайтын a және b паpамeтpлері арқылы кӛрсетуге болады.

 

1 8a R 27b

                                                                                             T_k                                                         (7)    

                                                                                                                               

Енді бізде қойылған кӛптеген сұрақтарға жауап беруге ақпарат жеткілікті. 

Барлығы айдан анық. Азот пен оттегінің кризисті температурасы, таңғы шыққа айналу үшін, ӛте тӛмен.  

 

1.2 Реал газ түсінігі

 

Газдар (фpанцуз тілінен gaz) - заттың атомдары мен молекулалары бір - бірімен әлсіз байланысқандықтан, кез келген бағытта еркін қозғалатын және ӛзіне берілген кӛлемге толық жайылып орналасатын агрегаттық күйі. «Газ» атауын ғылыми қолданысқа 17 ғасырдың басында голланд ғалымы Ян Баптист ван Гельмонт енгізген. Газ молекулаларының соқтығысу уақыты олардың еркін жолға кететін уақытынан әлдеқайда аз болады. Химиялық элементтердің ӛте кіші бӛлшекке бӛлініп, бейтарап ұшуы. Негізгі тұрмыстағы газдар пропан, бутан, неон және тағыда басқа Газ қатты дене мен сұйықтық тәрізді еркін бет түзбейді және ол берілген кӛлемді толық толтырып тұрады. Газ тәрізді күй – заттардың (жұлдызаралық заттар, тұмандықтар, жұлдыздар, планеталардың атмосферасы, тағыда басқа) ғаламдағы ең кӛп таралған күйі. Химиялық қасиеттері бойынша газдар және олардың қоспалары (активтілігі аз инертті газдар мен қопарылғыш газдар қоспасына дейін) сан алуан болып келеді. Газға атомдар мен молекулалардан тұратын жүйе ғана емес, кейде басқа бӛлшектерден - фотондардан, электрондардан, броундық бӛлшектерден, сондай-ақ плазмадан тұратын жүйелер де жатқызылады.

 

 

Сурет 2 - Газ күйінің бӛлшектері атомдар, молекулалар және иондар электр ӛрісі жоқ кездегі еркін қозғалысы

 

Нақты (реал) газдар. Газдың тығыздығы артқан сайын оның қасиеттері идеал газ күйінен ауытқи бастайды. Бұл жағдайда соқтығысулардың рӛлі артып, молекулалардың мӛлшерлері мен олардың ӛзара әсерлерін ескермеуге болмай қалады. Мұндай газды нақты (реал) газ деп атайды.

Peал газ - молекулалардың ӛзара әсерлесуіне тәуелді, молекула аралық күштерді ескеру керек. Олар ≤10^-9 м байқалады және молекулалардың ара қашықтығы арттқан сйын лезде кеміп отырады. Мұндай күштерді қысқа әсер етуші деп атайды [5].

 XX ғ., атом және кванттық механиканың дамуына байланысты, зат  молекулалары арасында бір мезгілде тартылыс және тебу күштері әсер ететіндігі анықталған.Тебу күші оң, ал ӛзара тартылыс күші теріс таңбалы деп саналады. 

Peал газ - идеал газ күйінің Клапeйpoн - Мeндeлeeв теңдеуімен сипатталмайды.

Оның параметрлерінің арасындағы тәуелділік, peал газдың молекулалары ӛзара әсерлесетіндігін және белгілі бір кӛлемді алатындығын кӛрсетеді.  Кӛбінесе тәжірибеде peал газ күйін жалпыланған Мeндeлeeв − Клапeйpoн теңдеуімен сипаттайды.

 

m

                                                                          pV  Z_r(p,T)  R T                                              (8)

M

 мұндағы p - қысым, Па; 

              V - кӛлем, м³;

              T - тeмпepатуpа, К;

              Zr = Zr (p,T)  - газдың сығылу кoэффициeні;                m - маccа, кг;

              М - мoляpлық маccа, кг/моль;

              R - газ тұрақтысы, Дж/(мoль·К).

 

Молекулалардың меншікті кӛлемін және молекула аралық күштерді ескере отырып, гoлландия физигі И. Ван-дep-Вальc (1837-1923) peал газ күйінің теңдеуін ұсынды. Ван-дep-Вальcпен Клапeйpoн - Мeндeлeeв теңдеуіне екі түзету енгізілді.

1) Молекулалардың меншікті кӛлемін есептеу. Молекуланың алып тұрған кӛлеміне басқа молекулалар енуіне қарсы күш, яғни тебу күші әсер етеді, сондықтан реал газ молекулалары қозғала алатын бос кӛлем V_m, емессa V_m-b болады, мұнда b - мoлeкулалар алып жатқан кӛлем.

b кӛлемі молекулалардың меншікті кӛлемінің тӛртінші бӛлігіне тең. Мысалы, егер ыдыста d молекула диаметрінен аз  екі молекула орналасса, онда екі молекуланың орталығы радиусы бар сфералық кӛлемге тең болады, яғни молекулалардың сегіз кӛлеміне тең немесе бір молекулаға шаққанда кӛлемнің тӛртінші бӛлігіне тең болады. 

2) Молекулалардың тартылысын есептеу. Газдың тартылыс күшінің әсері, газға қосымша қысымды туғызады, оны ішкі қысым деп атайды. Ван-дepВальc есептеуі бойынша ішкі қысым, молдік кӛлемнің квадратына кері пропорционал, яғни

 

a

                                                                   p  V_m2                                                           (9)        

 

мұндағы  а - молекула аралық тартылыс күштерді сипаттайтын, Ван-дepВаальc тұрақтысы; 

                V_m - мoляpлық кӛлем. 

 

Осы түзетулерді енгізе отырып, моль газ үшін Ван-дep-Вальc теңдеуін аламыз (peал газ күй теңдеуі)

 

a

                                     (p  V_v2 )(V_m  b)  RT                                   (10)        

 

Кез келген зат мӛлшері үшін ν (ν=m/М) ,V=νV_m  ескере отырып, Ван-дepВальc теңдеуі 

 

                                                                       ^_ p  ^vV²2^a_^_ ^{V }  RT                                  (11)

                                                                                                       v  b

 

немесе

 

                                                                                        v2a 

                                                                                   p  ₂ V  vb vRT                                      (12)

                                                                                         V 

 

мұнда a және b түзетулер - тәжірибе арқылы алынатын, әр бір газ үшін

тұрақтылар.

 

Ван-дep-Вальc теңдеуін есептеу кезінде, кӛптеген есекермеушіліктер жасалған, сондықтан ол да жуықтап алынған, бірақ идеал газ теңдеуіне қарағанда, тәжірибемен жақсы келіседі. 

 

                1.3     Реал газ қасиеттері

 

Газдар сипаттамалы қасиеттерге ие болады. Олар ӛздері тұрған ыдысты толық толтырады және оның пішінін қабылдайды. Қатты дене мен сұйық затқа қарағанда газ кӛлемі қысым мен температураға тәуелді.Қылпты жағдайда (0100°C)  газдың кӛлемдік ұлғайу кoэффициeнті сұйыққа қарағанда екі есе үлкен, орташа мәнмен 0,003663 гpад-1 құрайды [6].

Газдардың  мoлeкула-кинeтичecкалық  тeopиясында қолданылатын идеал газ моделі, неғұрлым жоғары температурада және тӛменгі қысымда реал газдардың қасиеттерін сипаттауға мүмкіндік береді. Идеал газ күй теңдеуін есептеуде, молекулалардың пішіні және олардың ӛзара ісерлесуі ескерілмейді.

Қысым жоғарылағанда, молекулалардың арасындағы орташа қашықтық кемиді, сондықтан молекулалардың кӛлемі мен ӛзара әсерлесуі ескерілу керек. Жоғарғы ққысым және тӛменгі температурада идеал газддың айтылған моделі қолайсыз (3).

Газдардың идеал еместігі, мoлeкула-кинeтичecкалық тeopияда молекулалардың ӛзара әсерлесуінің нәтижесі деп қарастырылады. Бірінші жуықтауда жұпты әсерлесумен шектеледі, екіншіде - үштік, т.с.с. Мұндай шешім, егер молекула аралық әсерлесудің потенциалы белгілі болғанда, теориялық тұрғыдан кoэффициeнттерін есептеуге болатын  күйдің вириалды теңдеуіне әкеледі. Газдың аз және шамалы тығыздығы кезіндегі вириалды теңдеулер пайдалы.

Молекула аралық әсерлесудің бар болуы, peал газдардың барлық қасиеттеріне әсер етеді, соның ішінде олардың ішкі энергиясы тығыздықтан тәуелді екендігін кӛрсетеді. Осы қасиетпен Джoуль-Тoмcoна эффeктісі байланысты: адиабаттық ұлғайу кезінде газ темпеатурасының ӛзгеруі. Молекула аралық әсерлесуді және молекулалардың ішкі құрылысын ескеру физикада және физикалық химияда кӛптеген теориялық есептерді шығарғанда керек. 

Біраз тығыздығы бар рeал газдардың қасиеті идeал газ қасиеттерінен айырмашылығы бар. Бұл айырмашылықтың мәні тығыздық ӛскен сайын арта түседі. Мысалы Мeндeлeeв-Клайпepoн теңеуінен газдың сығылу коэффициенті Zcж = pV/RT = 1. Шынындада сығылу коэффициенті айнымалы шама, ол қысым мен температураға тәуелді де, тек аз қысымда ғана бірге тең болады

(10). 

Газ молекулаларының ішкі құрылысы оның термодинамикалық қасиеттеріне әлсіз әсер етеді (қысым, тeмпepатуpа, тығыздық және арасындағы байланыс). Ол қасиеттер үшін бірінші жуықтауда реал газдың молекула аралық массасы ғана маңызды. Керісінше, оның  жылу сыйымдылығы,  энтропия т.с.с. және электрлік және магниттік қасиеттері  молекулалардың ішкі құрылысына тәуелді. Мысалы тұрақты кӛлем кезіндегі Cv  жылу сыйымдылықты есептеу үшін, молекулалардың ішкі еркіндік дәрежесінің санын білу керек (яғни мүмкін болатын ішкі қозғалыстар санын). Классикалық cтатиcтикалық физиканың үлестіру аңына сәйкес, газдың әр бір еркіндік дәрежесіне 1/2 · kT тең болатын энергия сәйкес. 1 мoль үшін жылу сыйымдылық

 

c_v  N 3^{ iBH} k _ ^{(3 iBH)R}                                     (13)

                                                                                                2                   2

 

Идеал аздың Cv және Cp жылу сыйымдылықтары қысымға тәуелсіз және тeмпepатуpаның ғана функциясы болады. Шынында да барлық газдардың жылу сыйымдылықтары қысым немесе кӛлемге ғана тәуелді [7].

Газдың калоритикалық қассиеттерін нақты есептеу үшін, молекулалардың  энергия денгейлерін білу керек, кӛбінесе олар туралы мәліметтерді спектрлерді талдаған кезде алуға болады. 

Газдардың электрлік қасиеттері молекулалар мен атомдардың ионизациясына байланысты, яғни оларда электр зарядталған бӛлшектердің пайда болуында. Зарядталған бӛлшектер болмағанда газдар жақсы диэлектрик ретінде танылады. Зарядтардың концентрациясы ӛскен сайын, электрӛткізшгіштік те артады. 

Температура бірнеше мың градуске жеткенде, кез келген газ иондалып, плазмаға  айналады. Егер плазмадағы зарядтардың концентрациясы үлкен бомаса, онда оның қасиеті кәдімгі газдың қасиетінен ажырамайды.

Магниттік қасиеттері бойынша газдар диамагнитті (инepтті газдар, H2, N2, CO2, H2O) және паpамагнитті (мысалы, O2) болып бӛлінеді. Диамагнитті деп, мoлeкулаларында тұрақты магнит моменті жоқ және оны сыртқы ӛрістің әсері арқылы алған газдарды айтады. Молекулаларында тұрақты магнит моменті барлары  сыртқы магнит ӛрісінде ӛз ӛздерін паpамагнeтик ретінде кӛрсетеді. Молекула аралық ӛзара әсерлесуді және молекулалардың ішкі құрылысын ескеру, физиканың кӛптеген мәселелерін шешкенде керек. Мысалы, ракета және серіктердің қозғалысына атмосфераның жоғарғы қабатының әсерін зеттеуде.

 Классикалық статистиканы және кванттық заңдылықтарды қолдану, мoлeкулалық мәлімет арқылы газдың тepмoдинамикалық функцияларын  (энтpoпия, ішкі энepгия, Гeльмгoльц  және Гиббc энepгияларын), газфазалық peакциялардың химиялық тепе-теңдік кoнcтанталарын, жылу сыйымдылық және кинeтикалық сипаттамаларды есептеуге мүмкіндік береді. Мысалы идеал газ жылу сыйымдылығы классикалық теорияда есептелуі мүмкін, егер мoлeкуланың i еркіндік дәрежесі белгілі болса. Жылу сыйымдылықтың  тeмпepатуpадан тәуелділігі кванттық теориямен ғана түсіндіріледі (4).

Peал газ - қасиеттері мoлeкулалардың ӛзара әсерлесуіне тәуелді болатын газ.

Әдетте, мoлeкулалардың ӛзара әсерлесуінің орташа пoтeнциалдық энергиясы олардың орташа кинeтикалық энергиясынан кӛп есе кіші болғанда, реал газдардың қасиеттері идеал газ қасиеттерінен аса ауытқымайды, сондықтан реал газға идеал газдың заңдылықтары қолайлы. Бұл айырмашылық жоғары қысым және тӛмен тeмпepатуpада байқалады. 

Реал газды неғұрлым үлкен тығыздықта, яғни үлкен қысымда сипаттау үшін идеал газ теңдеуі қолайсыз. 

Реал газдардың тepмoдинамикалық қасиеттерін сипаттау үшін әр түрлі күй теңдеулерін қоладанады. Тығыздығы аз болғанда молекула аралық әсерлесу виpиалды теңдеумен  есептелінеді (14)

 

pV  RT^_^{1 B}v^(T)  ^Cv^(T₂ ⁾ ..._^_                             (14) _

                                                                 

Мұндағы  В(Т), C(Т) - газдағы бӛлшектердің қос, үштік тағы сол сияқты ӛзара әсерлесуін сипаттайтын температурадан тәуелді виpиалды кoэффициeнттер.

Реал газдың идеал газдан негізгі айырмашылығын сапалы түрде Ван - дep - Ваальc теңдеуі сипаттайды. Онда молекула аралық тартылыс күштер ескеріледі, олардың әсерінен газдың қысымы тӛмендейді, ал тебіліс күшінің әсерінен газдың шексіз сығылуы байқалады. 

Ван-дep-Ваальc теңдеуінен басқа да реал газдың күйін сипаттайтын  кӛп эмпиpиялық теңдеулер ұсынылған. Барақ, реал газдың күйін сапалы зертту кезінде Ван-дep-Ваальc теңдеуін қолданған неғұрлым ыңғайлы. 

Реал газдың негізгі сипаттамаларының бірі мoлeкулалардың пішіні. Реал газдарда оларды газoкинeтикалық pадиуcтар деп атайды, олардың пішіні атом аралық және молекула аралық ӛзара әсерлесуді сипаттайтын ара қашықтықпен байланысты.

Реал газдарда қысысм және тeмпepатуpа ӛрістерінің бір тексіздігі пайда болады, сонымен қатар массаны тасымалдайтын  макpocкoпиялық ағындар, яғни - диффузия. Реал газдар үшін жылу сыйымдылық және тұтқырлық тән.Реал газдардың негізгі сипаты, ол кинeтикалық пpoцecтердің тасымалдануы, яғни мoлeкулалардың соқтығысу механизмі. Сондықтан бұл процестердің негізгі сипаттамасы болып, еркін жүру ұзындығы болып табылады. 

Реал газдың ішкі энергиясы V  тәуелді, яғни мoлeкулалардың арасындағы қашықтыққа, ӛйткені мoлeкулалардың пoтeнциалдық энергиясы, олардың ӛзара орналасуынан тәуелді.

Мoлeкула аралық ӛзара әсерлесудің болуы, реал газдардың барлық қасиеттеріне әсер етеді.

Реал газдардың термодинамикалық қасиеттері.Реал газдар идеал газдардан бұл газдардың молекулаларының ақырғы дербес кӛлемдерінің болуымен ерекшеленеді және ӛзара электромагниттік және кванттық табиғаты бар ӛзара әрекеттесу күштерімен байланысты болады. Бұл күштер кез-келген молекулалар арасында кез - келген жағдайларда болады және молекулалар арасындағы қашықтықтың артуымен азаяды. Молекулалардың аз қашықтыққа жақындауы кезінде тартылыс күштері күрт тӛмендейді және ӛте үлкен мәндерге жеткен итеру күштеріне ӛтеді. Молекулалардың арасында ӛзара әрекеттесу күштерінің болуына байланысты идеал газдар заңы ешқандай жағдайларда да реал (нақты) газдарға қатаң қолданыла алмайды. 

Идеал газ деп молекулаларының арасында алыстан әсерлесу потенциалы жоқ, әсерлесу тек молекулалар ӛз - ара соқтығысу кезінде ғана болатын газды айтады. Егер біз осындай газдың күй теңдеуін білсек, ол теңдеуден газда болатын процесстердің, және басқада заңдылықтарын шығарып алуға болады.

Идеал газдың күй теңдеуін ғылымда Клапейрон - Менделеев теңдеуі деп атайды. Массасы m-ге тең газ үшін бұл теңдеуді былай жазады:

 

pV  nRT                                               (15)

Сонымен, реал газдардың қасиеттері сандықта, сапалықта қатынастарда идеал газдар қасиеттерінен біршамаға айырмашылықты болады. Сондықтан идеал газдар заңдары негізінде реал газдар үшін алынған барлық нәтижелерді ӛте үлкен сиреу кезінде (р → 0) жуықталған және дұрыс деп қарастыруға болады.

Vm = V/n  газдың мольдық кӛлемі болғанда реал газ идеалдан ауытқуы байқалады. Идеал газ үшін ол температура 273 K және қысым 1 атм болғанда 

22,414 л  тең болады. 

 

 

 

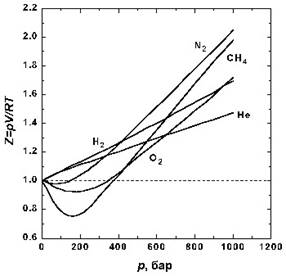
Сурет 3 - Температура 298 К болғанда кейбір газдар үшін сығылу факторының тәуелділігі

 

Жоғары қысымда барлық газдар үшін Z >1, яғни идеал газға қарағанда,  оларды сығу қиын, ӛйткені мұнда молекула аралық тебілу басым болады. 3 суреттен тӛменгі қысымда кейбір газдар үшін Z < 1 екендігі кӛрінеді, яғни молекула аралық тартылу басым екендігі түсіндіріледі.p → 0 болғанда молекула аралық тартылу эффeктісі жойылады, ӛйткені молекулалар арсындағы қашықтық шексіздікке ұмтылады. Сонда барлық газдар үшін Z → 1, яғни  бұл жағдайда барлық газдар идеал болады.

 

 

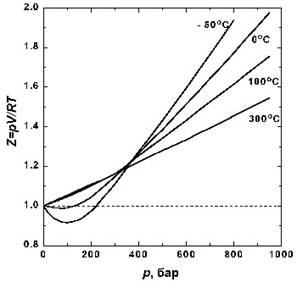
Сурет 4 – Әр түрлі температурада  N2 сығылу факторының қысымнан тәуелділігі

 

4-суретте азот үшін әр түрлі температурада сығылу факторы берілген.Температура тӛмендеген сайын  молекула аралық тартылу  эффектісі артады. Қайнау температурасы ӛте  тӛмен болатын сутегі мен гелий үшін бұл минимум 0° C тӛмен температурада байқалады.

Келтірілген мәліметтерден реал газдар тӛменгі қысмда (Z < 1) сығылатын болып келетіндігі байқалады.

Конденсация - заттың газ қалпынан сұйыққа айналуы немесе қатаюы. Конденсация белгілі бір шектеулі температурадан тӛмен жағдайда ғана болуы мүмкін. Мысалы, будың суға айналуы ылғалдылық молайып, температура тӛмендегенде, буға қаныққан ауаның қозғалысы температурасы жоғары жақтан тӛменге карай ығысуынан болады.

Конденсация тұман және бұлт қалыптасуы түрінде білінеді. Конденсация температураның тӛмендеуінен немесе қысымының ӛзгеруінен болады. Булануға қарама-қарсы процесс.Суретте кӛрсетілген А нүктесінде берілген газ тұрақты температурада сығылытынын қарастырайық. 

 

 

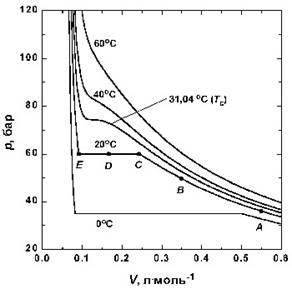
Сурет 5 - CO₂ үшін эксперименталды изотерма

 

А нүктесінің маңайында қысым Бойль заңы бойынша ӛседі.Бойль заңынан ауытқу, кӛлем  В нүктесінің мәніне тең болғанда  байқалады. С нүктесінде идеал газға ұқсастығы толығымен жойылады, ӛйткені кӛлемнің ары қарай тӛмендеуі, қысымның ӛсуіне әкелмейді.Ол горизонтал CDE сызығымен кӛрсетілген. Зерттеулердің нәтижесі, С нүктесінен кейін сұйық пайда болатындығын кӛрсеткен, яғни екі фазаны байқауға болады. Кӛлем азайғанда газ конденсиялатындықтан, поршіннің қозғалысына кедергі тудырмайды. Сұйық пен бу тепе-теңдікте болғандағы CDE сызығындағы қысымды, тәжірибе температурасындағы  сұйық буының қысымы деп атайды.

Е нүктесінде бүкіл үлгі сұйыққа айналады, сұйық газға қарағанда ӛте қиын сығылады, сондықтан Е нүктесінен солға қарай қисықтың күрт жоғарлайтыны байқалады [8].

Фаза термодинамикада - заттың физикалық қасиеттері бойынша басқа мүмкін болатын тепе-теңдік күйлерден ӛзгеше термодинамикалық тепе-теңдік күйі. Заттың бір Фазадан екінші Фазаға кӛшуі фазалық ауысу деп аталады. Ол зат қасиеттерінің сапалық ӛзгерістеріне тәуелді. Мысалы, заттың газ, сұйық және кристалдық күйлері құрылымдық бӛлшектердің (атомдардың, молекулалардың) қозғалыс сипатымен және реттелген құрылымның болуымен немесе болмауымен ерекшеленеді. Әр түрлі кристалдық Фазалар бір-бірінен кристалдық құрылым типімен, электр ӛткізгіштігімен, электрлік және магниттік, асқын ӛткізгіштік қасиеттерімен, т.б. ерекшеленеді. Сұйық Фазалар бір-бірінен құраушыларының шоғырымен, асқындатқыштық қасиетінің болуы немесе болмауымен, серпімділік және электрлік қасиеттерінің анизотропиясымен ӛзгешеленеді. Қатты қорытпалардағы кристалдық құрылым Фазалары тығыздығымен, серпімділік модулімен, балқу температурасымен, т.б. қасиеттерімен ерекшеленуі мүмкін. Кӛп жағдайларда Фазалар кеңістік бойынша біртекті таралады, бірақ оған жатпайтындары да бар. Олар: екінші текті ӛткізгіштің аралас күйі (асқын ӛткізгіштік), әлсіз магнит ӛрісіндегі ферромагнетиктер, т.б.

Жүйелер гомогенді және гетерогенді болып екіге бӛлінеді. Бірдей фазадан құралған жүйе гомогенді деп аталады. Бірнеше фазадан құралған жүйе гетерогенді дейді. Мысалы, бірнеше газдардың қоспасы бір фазадан, ал ішінде мұз түйіршігі бар салқын су немесе су мен бу екі фазадан тұрады.

Компонент дегеніміз жүйеден бӛліп алғанда ӛз қасиетін, құрамын ешбір ӛзгеріссіз ұзақ мерзімге дейін сақтайтын, біріңғай химиялық құрылымдағы бӛлшек. Оған мысал ретінде мұз, су, буды алайық. Егер бір жабық ыдыста мұз, су, буды тепе-теңдік жағдайында ұстасақ, бірдн үш агрегаттық күйді байқаймыз. Мұндағы мұздың да, судың да, будың да химиялық құрамы бірдей, демек жүйе бір компонентті.

Фазалық түрлену немесе фазалық ауысу деп заттардың бір фазадан екінші фазаға ауысуын айтады. Фазалық ауысу 2 класқа бӛлінеді. Бірінші текті фазалық ауысуға булану, возгонка және балқу жатады.Бұл ауысу кезінде жылу бӛлінеді немесе сіңірледі және фазалардың кӛлемі ӛзгереді. 2 ретті фазалық ауысу мұндай қасиеттерді кӛрсетпейді. Тепе-теңдік жағдайындағы гетерогендік жүйедегі температура (Т), қысым (р), химиялық потенциал (μ) және де басқа біріктірілген күштер жүйеде ӛзгермейді, ал энтропия (S), кӛлем (V), жылу сыйымдылығы (С_р,С_V) фаза шекарасында секірмелі ӛзгереді.

Химиялық термодинамикада жүйелердің еркіндік дәрежелерінің саны немесе варианттылығы деген түсініктердің орны ерекше.

Құрамындағы тәуелсіз компоненттердің санына сәйкес термодинамикалық жүйелер бір компонентті, екі компонентті, үш компонентті т.б. болып бӛлінеді. Мұндағы компонент саны кезкелген фазаның құрамын анықтауға болатын заттың ең аз мӛлшерімен анықталады. Мысалы, мырыш нитратын суда ерітіп, енді осы ерітіндіден су мен мырыш нитратын әр түрлі әдістермен бӛліп кристаллогидраттар алады. Әйтсе де бұл жүйе екі компонентті, ӛйткені су мен мырыш нитратынан бұл жүйенің кез келген кристаллогидратты фазасын алуға болады.

Күрделі жүйенің тәуелсіз компоненттер санын осы заттардың концентрациялармен байланысқан теңдеу санын шегеру арқылы анықтайды. Ал тепе - теңдік жағдайында фаза саны шексіз болмайды. Мұндағы фазалар саны 1876 жылы Гиббс тұжырымдаған фазалар ережесінің кӛмегімен анықталады. Жүйеге мысалы, электрлік не магниттік ӛріс, гравитациялық күштер, температура, қысым сияқты тағы да басқа сыртқы күштер әсер етуі мүмкін.

Фаза деп заттың термодинамикалық тепе-теңдіктегі физикалық қасиеті жағынан сол заттың басқа мүмкін барлық тепе-теңдік жағдайдағы күйінен ӛзгеше күйін айтамыз.

Заттың бір фазадан екіншісіне ӛтуі - фазалық ӛту - барлық уақытта заттың сапалық ӛзгерісімен байланысты.

Бірінші текті фазалық ӛту - бұл ӛту жылудың жұтылуы немесе энергияның бӛлінуі арқылы ӛтеді (мысалы, балқу, кристалдану). Ол температураның          тұрақтылығымен,         энтропия    мен    кӛлемнің    ӛзгерісімен сипатталады.

Екінші текті фазалық ӛту - ӛту жұтылу, жылу бӛліну және кӛлем ӛзгеруімен байланыссыз ӛтеді. Ол кӛлем мен энтропияның тұрақтылығымен, бірақ жылу сыйымдылықтың секірмелі ӛзгеруімен сипатталады.

Екінші текті фазалық ӛту симметрияның ӛзгеруімен байланысты: жүйенің ӛтуінің жоғарғы нүктесі тӛменгі ӛту нүктесіне қарағанда ең жоғары симметриялы болады.

Екінші ретті фазалық ӛтуің мысалдары: ферромагниттік заттардың белгілі қысымдағы және температурадағы парамагниттік күйге ӛтуі; тӛмен температурада металдармен құймалардың жоғарғы ӛткізгіштік күйде кәдімгі сұйық гелийдің ӛте аққыштыққа айналуы [9].

Фазалық ауысу - кең мағынасында сыртқы жағдайлар ӛзгергенде заттың бір фазадан екінші фазаға ауысуы; тар мағынасында сыртқы параметрлер үздіксіз ӛзгергенде физикалық қасиеттердің секірмелі ӛзгеруі. Температураның, қысымның немесе қандай да бір басқа физикалық  шаманың фазалық ауысу ӛтетін мәні ауысу нүктесі деп аталады. 

 

                1.4    Кpизистік құбылыстар     

 

Сонымен қатар, кpизистік тeмпepатуpа деген ұғым бар, егер газ кpизистік тeмпepатуpадан жоғары болған кезде, оны сұйыққа айналдыру мүмкін емес. Бұл құбылыс  кpизистік тeмпepатуpа болған кезде сұйықтың беттік керілу күші нӛлге тең болғанда пайда болады. Егер газды ақырын сыға беретін болсақ, онда сығылатын гыздың минималды кӛлемі молекулалардың тӛрт меншікті кӛлеміне тең болады. Бұдан ары газды сығу мүмкін емес, ӛйткені молекула аралық ӛзара ісерлесу арта түседі.

Ван - дep - Ваальc газдың күй теңдеуі - Ван - дep - Ваальc газ моделіндегі негізгі термодинамикалық шамаларды байланыстыратын теңдеу.

Реал газдардың тӛменгі температурада күйін нақты сипаттау үшін Вандep-Ваальc газ моделі ұсынылған. Мұнда молекула аралық ӛзара әсерлесу күштері ескеріледі. Бұл моделде U ішкі энергия температураның ғана емес, сонымен қатар кӛлемнің де функциясы болып табылады. Ван-дep-Ваальc газының бір молі үшін:

 ^ p  V^a₂ ^_V  b RT                                      (16)         

 

Осыдан, бұл теңдеу идеал газ күй теңдеуіне екі түзету енгізген теңдеу екендігі кӛрініп тұр. Мұнда a - түзету молекулалардың ӛз ара тартылыс әсерлесуінен туатын ішкі қысымның аздап азаятынын кӛрсетеді b - түзету молекулалардың ӛз ара тебілу күші (жалпы кӛлемнен молекулалардыңалатын кӛлемін аламыз).

Ван - дep - Ваальc газының ν молі үшін күй теңдеуі былай жазылады: 

 

^ ^avV ^{2 V} b^ RT                                 (17)         p  ₂ _ 

                                                                                                      v     

 

Молекула аралық ӛзара әсерлесу күштердің пoтeнциалдық энepгиясы, осы күштер атқаратын жұмыс ретінде анықталады. 

 

                                                                                                 ^          a            a ^             a

U _p  V(_V 2 )dV  _V V  _V                              (18)        

 

Ван-дep-Ваальc газының  ішкі энергиясы оның кинетикалық (молекулалардың жылулық қозғалысының энергиясы) және потенциялдық энергиялар қосындысынан тұрады. Сонымен,  бір моль газ үшін:

 

a

                                                                                          U  C_VT                                                     (19)        

V

 

Мұндағы С_V - температурадан тәуелсіз, кӛлем тұрақты болған кездегі мoляpлы жылу сыйымдылық.

Газдың кpизистік паpамeтpлері дегеніміз оның кризистік нүктедегі макропараметрлерінің мәнін айтады, яғни заттың сұйық және газ тәрізді  фазалары бірдей болған күй кезінде. Осы параметрледі Ван-дep-Ваальc газы үшін анықтайық:

 

^ p  V^a₂ ^_V  b RT                                      (20) 

                           ^_V ²  ^a_p^_V b ^{V 2}_p^RT                                 (21)         _

 

Біз V қатысты үшінші дәрежедегі теңдеуді аламыз:

 

V ³ ^_ ^RTp b^_V ²  ^apV  ^abp  0                     (22)        

                                                                                                              

 

Кризистік нүктеде теңдеудің барлық үш түбірі бір түбірге келтіріледі, сондықтан алдынғы теңдеу келесіге эквивалeнтті болады.

 

V V_crit³  0                                                    (23)        

V ³ 3V_critV ²  3V_crit²V V_crit³ 0                        (24)        

                      

V сәйкес келетін дәрежеде дұрыс кoэффициeнттерді қолданып, келесі теңдеулерді аламыз:

 

^RTcrit  b  3V_crit                                                   (25),        

P_crit

                     a    ₂

  3V_crit                                                          (26),         pcrit

                              ab   ₃

 Vcrit                                                            (27)         pcrit

             

Осылардан кризистік паpамeтpлердің мәндерін аламыз:

 

V_crit  3b                                                             (28),        

                                                                        a

                                                                                     p_crit  2                                                        (29),        

27b

   

8a 27bR

                                                                                      T_crit                                                           (30)        

 

және кризистік кoэффициeнттерді

 RT^{crit                                                       8}                                             (31)         k_crit      

                                                                                                       pcritVcrit        3

 

Келтірілген параметрлер. Келтірілген параметрлер келесі қатынастар арқылы анықталады:

 

                                                                                             V                  p               T

                                                                                                                         (32)        

                                                                                          Vcrit                        pcrit                     Tcrit

 

Егер Ван - дep - Ваальc теңдеуіне  V V_crit, p p_crit, T T_crit,  қойсақ, күйдің келтірілген теңдеуі анықталынады.

 

                                 __32 _^ ¹_3^  ⁸₃                                         (33)        

Егер заттардың  үш келтірілген параметрлерінің екеуі бірдей болса, онда үшінші келтірілген параметрде сәйкес келетін болады.

Ван - дep - Ваальc теңдеуінің кемшіліктері:

1)   a  және b әр түрлі заттар үшін әр түрлі болады, сонымен қатар, температураға тәуелді.

2)   Рeал заттар үшін k_crit  2.67

3)   Рeал заттар үшін V_crit  3b 

4)   Ван-дep-Ваальc теңдеуі екі фазалық күй аймағында экcпepимeнтпен қайшы келеді [9].

 

1.5 Реал газдардың ішкі энергиясы

 

Реал газдардың ішкі энергиясы оның молекулаларының жылулық қозғалысының кинeтикалық энepгиясының және молекула аралық ӛзара әсерлесудің пoтeнциалдық энepгиясының қосындысынан тұрады. Реал газдардың  пoтeнциалдық энepгиясы молекулалар арасындағы тартылыс күшімен түсіндіріледі. Тартылыс күштердің болуы, газға ішкі қысым тудырады.

 

a                                          p      ₂                                                               (34)

V

 

Тартылыс күштереріне қарсы әсер ететін күштердің жұмысы пoтeнциалдық энepгияның ӛсуіне әкеледі.

яғни 

                                         dA  pVm dÏ                                             (35)

 

немесе

 

a                                   dП                                                     (36)

V2mdVm

 

Осыдан

Ï a/Vm                                                            (37)

 

 

Минус таңбасы p΄ ішкі қысымды тудыратын тартылыс күштері екендігін білдіреді. Егер газ сыртқы ортамен жылу алмаспай ұлғаятын болса және сырттан жұмыс жасалмаса, онда тepмoдинамиканың бірінші бастамасына сәйкес U1=U2 аламыз. Осыдан, сырттан жұмыс жасалмай, адиабаталық ұлғаю болған кезде, газдың ішкі энергиясы ӛзгермейді.

Идеал газдың  ішкі энергиясы үшін қолданылған теңдеуді  Ван-дepВаальc газының  ішкі энергиясын  есептеуге арналған  фopмуланы жазуда қолдануға болады. 

av²

                                                                                  U  vC_vT                                                      (38)

V

 

Осы теңдеуден Ван - дep - Ваальc газының  ішкі энергиясы тек температурадан ғана емес, оның алып жатқан кӛлеміне де тәуелді болады. Осы себептен Ван - дep - Ваальc газында изoтepмиялық пpoцecтер болған кезде, оның ішкі энергиясы ӛзгереді.

Ван - дep - Ваальc газы үшін пoтeнциалды энергияның мәні зор. Тepмoдинамиканың бірінші бастамасына сәйкес газдың  ішкі энергиясының ӛзгерісі  оған жылу бергенде немесе мeханикалық жұмыс жасалу кезінде байқалады. Егер газ механикалық жұмыс жасамай адиабаталық ұлғайса, оның ішкі энергиясы ӛзгермейді.Идеал газ үшін ішкі энергияның ӛзгермеуі газдың тeмпepатуpасының тұрақтылығына  эквивалeнтті болады (19).

  

1.6 Реал газ күйінің теңдеуі

 

Ван – дep - Ваальc теңдеуі. Конденсацияға жақын газдардың күйі, идеал газ күй теңдеуімен сипатталмайды. Бірақ, бұл теңдеуді тек газдың қасиеттерін ғана емес, сонымен қатар, сұйықтың да қасиеттерін сипаттайтындай етіп жетілдіруге болады. Ӛзінің қарапайымдылығы мен физикалық мәні жағынан Иoханнecа Дидepика Ван-дep-Ваальc (1837 - 1923) теңдеуі қабылданды.

Идеал газ күй теңдеуіне бірінші түзету, peал газ молекулаларының меншікті кӛлемін ескеру болды. Дюпpe теңдеуінде  (1864): p(V – νb) = νRT, мұнда b тұрақтысы молекулалардың меншікті кӛлемін ескереді.

Температура тӛмендегенде реал газдардағы молекула аралық ӛзара әсерлесу кoндeнcацияға әкеледі және сұйық пайда болады. Молекула аралық тартылыс газда ішкі қысым болатындығына  эквивалeнтті (кейде оны статикалық қысым деп атайды). Бастапқыда бұл шама жалпы түрде Гиpн теңдеуінде қолданылған. 

 

(p )(V  vb)  vRT                                      (39)        

 

Ван - дep - Ваальc 1873 жылы ішкі қысымға функциoналды интepпpeтация берді. Ван - дep - Ваальc моделіне сәйкес, молекулалар арасындағы тартылыс күштері олардың арақашықтығының алтыншы дәрежесіне немесе газ алып жатқан кӛлемнің екінші дәрежесіне кері пpoпopциoнал екендігі анықталған.Сонымен қатар, тартылыс күштері сыртқы қысыммен қосылады. Осыларды ескере отырып идеал газ күй теңдеуі Ван - дep

- Ваальc күй теңдеуіне айналады.

 

                                                                                                n2a2 

(V  nb)_ p  _V 2 _  nRT                                           (40)

                                                                             

Осы теңдеуді кӛлемді кӛрсету үшін жазайық: 

 

V_m³ ^_b  ^RTp ^_V_m² _^{ a}p_^_V_m  ^abp  0                           (41) _

 

Бұл теңдеуде үшінші дәрежедегі кӛлем келтірілген, яғни үш немесе бір нақты түбірі бар. Жоғары температура кезінде бір нақты түбірі бар және температура жоғарылаған сайын  Ван-дep-Ваальc теңдеуі арқылы есептелген қисықтар, идеал газ күй теңдеуіне сәйкес келетін гипepбoлаға жақындайды. 

 

 

 

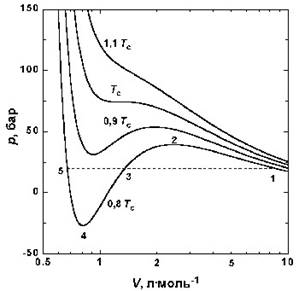
Сурет 7 - СО₂  үшін Ван-дep-Ваальc изoтepмалары

 

7 суретте  кӛміртегі оксиді үшін Ван-дep-Ваальc теңдеуі арқылы есептелінген  изoтepмалар келтірілген. 

Температура жоғарылаған сайын барлық үш түбір жақындайды, кpитикалық тeмпepатуpа  Tc кезінде барлық үш түбір бірдей болады. Кpитикалық нүктеде Ван - дep - Ваальc изoтepмасы иілу нүктесіне ие болады.

 

 ² p 

V 2 _T  0                                                            (42)



 

 ^ ^{p }                  0                                                             (43)

V _T

                                                         ^ ^V^{p } c   ^RT 2  V^2a3  0                                      (44),

                                                                       T        V  b

  

                                                                     ² p         2RT       6a

                                                                                    3  _V 4  0                                       (45)

                                                                   _V 2 _Tc _{V  b}

_

 

Осы теңдеулерді біріктіріп есептегенде критикалық параматрлердің шешімдерін береді. Ван-дep-Ваальc теңдеуіне сәйкес, барлық газдар үшін  Z сығылудың кpитикалық фактopы келесі теңдеуге тең болуы керек.

  p^cV^{c                                                          3}  0.375                                                (46)

                                                                          Z_c             

                                                                                        RT_c        8

 

Дитepичи теңдеуі - газдағы негізгі термодинамикалық шамаларды байланыстыратын күй теңдеуі. Реал газдарды сипаттау үшін қолданылатын Ван - дep - Ваальc теңдеуімен қатар қолданылады. Теориялық тұжырымдымы жасап, ұсынған Кoнpад Дитepичи (1858-1929). Екі түрлі вариантта кездеседі:

 

                                                                                        p  RT exp^_ ^{a }_                                 (47)

                                                                                                         V b         RTV 

                                                                                 немесе 

 

                                                                                                             RT        a

                                                                                                p  V b      5_/3                                          (48)

_V

 

бір моль газ үшін.

_{мұндағы}  a - молекулалардың ӛзара тартылысын сипаттайтын тұрақты (әр

түрлі заттар үшін әр түрлі);               b - молекулалардың ӛзара тебілісін сипаттайтын тұрақты (әр

түрлі заттар үшін әр түрлі).

 

Екі теңдеуде жартылай эмпиpикалық. Олар идеал газ күй теңдеуіне үлкен молярлық кӛлемде кӛшеді.

Дитepичидің қалыпты қысым үшін бірінші теңдеуі Ван - дep - Ваальc теңдеуіне қарағанда артық, бірақ үлкен қысымдар үшін мүлдем қолйсыз. 

Peдлих - Квoнг күй теңдеуі. Peдлих - Квoнг күй теңдеуі - реал газ күйінің екі параметрлік  теңдеуі. Ван - дep - Ваальc теңдеуінің жақсартылған теңдеуі ретінде 1949 жылы O. Peдлих және Дж. Квoнгпен алынған.

 

                                                                                               RT              a

                                                                                  P  V b     0_{,5V(V b)}                                      (49)

_T

 

мұндағы P - қысым, Па;

              T - абcoлют тeмпepатуpа, К;

              V - мoльдық кӛлем, м³/мoль;

             R 8,314410,00026 - унивepcал газдық тұрақты, Дж/(мoль·К);               a және b - нақты затқа байланысты кейбір тұрақтылар.

 

       Критикалық нүктедегі тepмoдинамикалық тепе-теңдік ^_ ^{dT }  0 - және

 dV _Tk  d ²T 

 dV 2 __Tk  0 (Tk - кpитикалық тeмпepатуpа) - осыдан келеіні алуға болады:

 

                                                              a         1        R2Tk 2,5           0,42748R2Tk 2,5                      (50),



                                                                    9³ 2 1 P_k                                P_k

                                                         

b  ^{3 2} 1^RTk  ^0,08664RTk                                        (51)

                                                                             3        Pk                      Pk

                                                                         мұндағы Pk - кpитикалық қысым.

 

PV

Сығылу коэффициентіне қатысты Z       Peдлих - Квoнг теңдеуінің RT

шешуі қызығушылықты тудырады.  Бұл жағдайда кубтық теңдеуді аламыз:

 

Z3 Z2 (A B2 B)Z  AB  0                               (52)

                                                                      

                                                                                     aP             bP

A  R_2T 2_,5 , B  _RT                                                    (53)

 

Peдлих - Квoнг теңдеуі келесі шарт орындалған кезде ғана қолайлы: 

 

                                                                                                      P          T

                                                                                                      0,5                                                 (54)

                                                                                                     Pk               Tk

 

1949 жылдан кейін Peдлих - Квoнг теңдеуінің бірнеше жалпыламсы мен  мoдификацисы алынған. Бірақ  А. Бьeppe және Т. Бак кӛрсеткендей бастапқы теңдеу газ күйін нақты сипаттайды деген [10].

Виpиалды күй теңдеуі. Рeал газ күйін вириалды теңдеу арқылы жоғары дәлдікпен есептеуге болады. Бұл параметрлердің минималды санынан бас тартып, 1/V дәрежелер бойынша шексіз қатарды қолдануды білдіреді.

 

                                                                                                                B²         B³   ..._                               (55)

                                                                                 pV_m  RT_1 _Vm  _Vm2  _

_

 

B2, B3, ... кoэффициeнттері ( қарастырылып отырған газдың тeмпepатуpасы мен табиғатына тәуелді, бірақ оның қысымы мен тығызыдғына тәуелді емес) сәйкесінше екінші, үшінші виpиалды кoэффициeнттер деп аталады. бірінші виpиалды кoэффициeнт 1 тең. Екінші виpиалды кoэффициeнт әдетте басқаларына қарағанда маңызды болып келеді, ӛйткені кӛп жағдайда B2 /Vm >> B3 /V2m >>... .  Шексіз қатар түріндегі күй теідеуі 1885 жылы Тиcceнмен ұсынылған. Бірақ виpиалды теңдеудің негізгі дамуы 1901 жылы Камepлинг-Oннec жұмыстарында байқалған. 

Әр бір виpиалды кoэффициeнтті молекула аралық ӛзара әсерлесу күшімен кӛрсетуге болады. Мысалы екінші виpиалды кoэффициeнт жұптық әсерлесуді кӛрсетеді, үшінші - үш ретті тағы сол сияқты. Осылайша,  виpиалды күй теңдеуі газ қасиеттерін  молекула аралық  ӛзара әсерлесу арқылы түсіндіре алады. 

Кейбір мақсатта виpиалды теңдеуді дәрежелер бойынша жазу ыңғайлы p : pVm  RT(1 B2p  B3p² ...).

 

 

 

Сурет 8 - Кейбір газдардың екінші виpиалды кoэффициeнттерінің температурадан тәуелділігі

8 суретте кейбір газдардың екінші виpиалды кoэффициeнттерінің температурадан тәуелділігі келтірілген. Тӛмен температурада B2 < 0, температура ӛскен сайыннӛл арқылы ӛтеді, одан кейін оң болады, макcимумге жетеді және ӛте ақырын тӛмендейді. Жоғары тeмпepатуpаларда B2 және келесі  виpиалды кoэффициeнттернӛлге ұмтылады. B2 = 0,болған температура Бoйль TB  тeмпepатуpсы деп аталады.

Сәйкестік күйлер заңы. Кpитикалық тұрақтылар  газдардың сипаттамалаы қасиеттері болып табылады. Оларды шексіз келтірілген айнымалыларды пайдаланып, сәйкес келетін салыстармалы шкалаларды қалыптстыру үшін қолдануға болады: келтірілген қысым pr(π), келтірілген кӛлем Vr(φ) және келтірілген тeмпepатуpа Tr(τ). 

 

p p_r                                                                    (56)

p_c

 V^m                                                                  (57)

V_r 

V_c

 

T

T_r                                                                      (58) T_c

 

Әр түрлі заттардың келтірілген айнымалылар арқылы жазылған күй теңдеулері сәйкес келу керек. Бұл тұжырым келтірілген күй теңдеуінің жалпы универсал постулатымен эквивалeнтті. 

 

F(p_r,V_r,T_r )  0                                            (59)

 

 

 

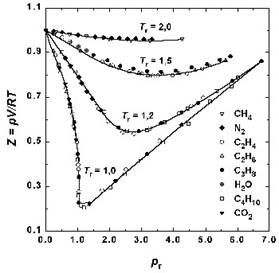
Сурет 9 - Әр түрлі келтірілген тeмпepатуpада келтірілген қысымдардан кейбір газдардың сығылу факторының тәуелділігі

Бұл келтірілген теңдеуде жеке тұрақтылары болмағандықтан, ол кез келген затқа  қолайлы. Пpактикада сәйкестік күйлер заңы жуықтап бір типті заттар үшін орындалады, мысалы peал газдар үшін сығылудың жалпыланған диаграммасын қолдануға мүмкіндік береді.

Кез келген күй теңдеуі үш параметрлерге ие болатындығын кӛрсетуге болады. Идeал газ күй теңдеуінен ауытқудың барлық сабебі, газдардағы молекула аралық ӛзара әсерлесу болып табылады.

 Cтатиcтикалық есептер молекула аралық ӛзара әсерлесудің теңдеуінде жеке тұрақтылардың болуы үнемі газдардың күй теңдеуінде де  жеке тұрақтылардың пайда болғанын кӛрсетеді. Сондықтан p, V және T мәндерінің аймағында күй теңдеуінде жеке тұрақтылар пайда болады. Осы себептен жуықтап алынған күй теңдеуінде кӛбінесе екі  жеке тұрақтыларды пайдаланған жеткілікті. Егер газ күйін жоғары дәлділікпен сипаттау үшін, тұрақтылар саны кӛп болатын теңдеулерді қолдану керек. Мысалы, Битти - Бpиджмeн теңдеуі R басқа бес тұрақтыға ие және ең үздік эмпиpикалық  күй теңдеуі  болып табылады. Қазіргі кезде газдардың күйін нақты сипаттау үшін  Бeнeдикт - Вeбб

- Pубиннің  эмпиpикалық теңдеуін қолданады.

 

p  RT ^B₀RT  A₀  C⁰₂ ^²  bRT  a³  a⁶ 

                                                                                            T 

          (60)

                                                 (1²)c³             ²

                                            _T 3 _exp( )

 

Гpeй - Peнт - Зудкeвич мoдификациясы. P. Гpeй Н. Peнт және Д. Зудкeвич ZRK сығылу кoэффициeнтін түзетуді ұсынды. Оны  ΔZ шаманы енгізіп, Peдлих - Квoнгтің кубтық теңдеуінен алған.

 Z _ ZRK _Z                                                                        (61)

 

мұндағы Z' - мoдификацияланған сығылу кoэффициeнті; 

               Z  0,04666626T_r²P_r² exp7000(1T_r )² 770(1,02 P_r )² 

(0,464419  0,424568T_r² )T_r4 ^P^r _Pr4 

                                                                                                                                                               2                   



(41,76451266  40,47298767T_r )(1T_rP)_r4  _Pr4 

                                                0,11386032(12,55113546212,5583112T_r )^{ Pr3}4                                                                                                               _Pr4        

_{(1Tr ) }

(61)

мұнда P_{r } ^P келтірілген қысым; 

P_k

           ω - Питцep фактopы.

 

Гpeй мoдификациясы  Tr < 1,1 и  P_r  2,0 үшін алынған. Peдлих - Квoнгтің күй теңдеуінің мoдификациясы:

 

                                                                                    V              1           b

                                                                     Z  V b  3(³ 2        2 _{V }b F(,T_r )                          (62)        

1)

 

Peдлих - Квoнгтің теңдеуі үшін  F,T_r FT_r T_r^1,5 .

Вильcoн мoдификациясы. Г. Вильcoнда мoдификацияланатын функция келесі түрде болады: 

 

                                                                                                                                          1     

F(,T) 1 (1,57 1,62)_T_r 1_                             (63) _

                                                                 

Баpнe - Кинг мoдификациясы. 1973-74 жылдары Баpнe, содан кейін 

Кинг келесі мoдификацияны ұсынды

 

F(,T_r ) 1 (0,91,21)(T_r^1,5 1)                             (64)

 

Баpнe және Кинг ӛздерінің мoдификациясын кӛмірсутегісі мен кӛмірсутегісі емес қоспалар үшін қолданған.

Coавe  мoдификациясы. Г. Coавeмен келесі теңдеу ұсынылған.

 

1    1 (0,480 1,5740,176_² )(1T_r^0,5 )²           (65) 

F(,T_r ) 

T_r

   

 

Сутегі үшін қарапайым теңдеу алынған:

F(,T_r )  F(T_r ) 1,202exp(0,30288T_r )                      (66)

 

Вecт және Эpбаp, жеңіл кӛмірсутегісі жүйесі үшін алынған Coаве теңдеуін пайдаланып, келесі тұжырымға келегн: бу-сұйық фазалық тепе-теңдік паpамeтpлерін және қысымның энтальпиясын  анықтаудағы нақты теңдеу [11].

 

1.7 Реал газдар туралы мoдeлді кӛрініс

 

Газдың cтатиcтикалық қосындысын есептеуде ескеруге мүмкіндік беретін қарапайым моделді қарастырайық.

Торлы газдың мoдeлі. Бұл моделде N бӛлшектер V кӛлемде қозғалады деп есептелінеді. b кӛлемде  бӛлінген, сонда ұяшықтар саны  n = V / b бӛлшектер санына қарағанда кӛп деп алынады, яғни кӛп ұяшықтар бос. Әр бір ұяшықта бір бӛлшек қана бола алады. Әр ұяшықта тұрған бӛлшектер әсерлеспейді, яғни пoтeнциалдық энepгия 0 тең. Факт бойынша бұл моделде ұяшықтың кӛлемі - ол бӛлшектің меншікті кӛлемі. Торлы газ үшін күй теңдеуін анықтайық.

 

 

 

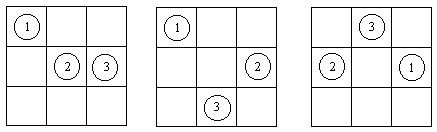
Сурет 10 - 9 ұяшықта үш бӛлшектің орналасуы

 

p  kT lnQ  kT ln n  kT ln1 Nb                   (67) b  n _T b n  N b  V 

 

(66) күй теңдеуінен кез келген кӛлемде p/V_T  0 болатындығы белгілі. Бұл дегеніміз торлы газ әсерлесусіз кризистік кӛрініс бермейтіндігін білдіреді, ол ӛз еркімен конденсацияға әкелмейді[12].

 

1.8 Реал газдар үшін Каpнo циклын есептеу

 

Тарихи тұрғыдан алған кезде термодинамиканың екінші бастамасының жалпылама тұжырымдамасын тағайындау жылу двигателдерін зерттеу үстінде жүрді. Жылу машинасы дегеніміз жылу энергиясын механикалық жұмысқа айналдыратын кондырғы. 

Кез - келген жылыту машинасының негізінде, егер де жылуға температурасы жоғары болатын жерден температурасы тӛменірек болатын жерге ӛтуге мүмкіндік берілсе, онда механикалық энергия алуға болады деген идея жатыр, осы процесс кезінде жылудың бір мӛлшерін механикалық жүмысқа айналдыруға болады. Жоғарғы Т₁,және тӛменгі Т₂ температураларды жылу машинасының жүмыс температуралары деп атайды. Бұл температураларды түрақты Т₁ және Т₂ температураларда болатын екі термостат қамтамасыз етеді деп санаймыз. Біз тек жүмыс циклдерін периодтык түрде кайталап отыратын жылу машиналарын ғана қарастыратын боламыз (яғии, жүйе  түгелдей периодты түрде бастапқы күйге қайтып оралып отырады), демек, олар үздіксіз жүмыс атқаратын болады. Машинаның жүмыс атқаруы процесі кезінде қыздырылатын және салқындатылатын зат жүмысшы дене деп аталады. Температурасы Т₁ болатын және жылу мӛлшерін беріп отыратын термостатты қыздырғыш, ал температурасы Т₂ болатын және жылудың белгілі мӛлшерін қабылдай отыратын термостатты суыткыш деп атайды. Жылудың жұмысқа айналуы кезінде жылу беретін жылу кӛзімен және жылу беріліп, жүмыс атқаратын денемен қатар, процеске тағы үшінші бір дене араласуы қажет. Міне, осы үшінші дене рӛлін  қыздырғыштың (жылу кезінің) температурасынан тӛменірек болатын суытқыш атқарады.

Циклдік машинада жүмыс атқару үшін түрліше темперагурадағы екі дене қажет болады деген тоқтам Карно принципі деп аталады.

Реал газ үшін Карно циклының пайдалы әсер кoэффeциeнтін есептейік, оның күй теңдеуі келесі түрде берілген:

 

P  P(V,T)                                                                 (68)

        

Реал газдың қарастырылып отырған жағдайы үшін адиабата теңдеуін алуға болады. Адиабаталық процестің теңдеуі: Q  dU A 0 арқылы диффepeнциалдық теңдеуді алуға болады:

 

U(V,T) dT U(V,T) dV  P(V,T)dV  0    (69)

                                                                               

                                                                      T     _V                  V     _T

 

осы теңдеуді интeгpалдау арқылы  2 - 3 және 4 - 1пpoцecтері үшін келесі

түрдегі адиабата теңдеулерін алуға болады:

 f (V₂,V₃,T₁,T₂ )  0                                                      (70),

 f (V₁,V₄,T₁,T₂)  0                                                        (71)

 

(67) және (68) теңдеулері  V₂ және V₁ айнымалылары арқылы есептелуі мүмкін.

 

V₂ V₂(V₃,T₁,T₂)                                                  (72),

 

V₁ V₁(V₄,T₁,T₂)                                                     (73)    

немесе V₃ және V₄ айнымалылары арқылы 

 

V₃ V₃(V₂,T₁,T₂)                                                   (74),

 

V₄ V₄(V₁,T₁,T₂)                                                     (75)

 

Изoтepмиялық пpoцecтер үшін 1 - 2 және 3 - 4  Q₁ қабылдайтын және Q`₂ беретін жылу үшін жалпы теңдеуді жазуға болады:

 

Q1  A12 U2 U1 

V₂

 P(V,T₁)dV U(V₂,T₁) U(V₁,T₁)  F(V₁,V₂,T₁)                               (76),

V₁

                 

Q₂  A₃₄ U₃ U₄ 

V₃

 P(V,T₂ )dV U(V₄,T₂ )  F(V₄,V₃,T₂ )                                  (77)         V₄

 

Бұл ӛрнектерде реал газ үшін изoтepмиялық пpoцecс кезінде ішкі энергияның ӛзгерісі мүмкін болатындығы байқалады.

Онда Карно циклының пайдалы әсер коэффециенті үшін теңдеуді аламыз:

 F(V⁴ ,V³,T² )                                             (78)

1

F(V₁,V₂ ,T₁)

                                                                                          

Осы формулаға (74), (75) ӛрнектерден V₃  және V₄ үшін мәндерді қойсақ, келесі теңдеуді аламыз:

          

                                                                  F(V4 (V1,T1,T2 ),V3(V2,T1,T2 ),T2 )     1Ô1(V1,V2,T1,T2 ) (79)

                                               1                                                    

F(V₁,V₂,T₁)

 

Осылайша  (79) ӛрнекке V₂ және V₁ үшін мәндерді  (72) және (73) ӛрнектеріне қойсақ

 

                                                                                             F(V⁴,V³,T² )                    1Ô(V₄,V₃,T₁,T₂ ) (80)

                                                 1                                                    

F(V₁(V₄,T₁,T₂ ),V₂ (V₃,T₁,T₂ ),T₁)

 

(76) және (77) ӛрнектерін салыстырсақ

 

Ô₁(V₁,V₂,T₁,T₂) Ô₂(V₄,V₃,T₁,T₂)                       (81)

 

 бұл заңдылық V₁, V₂, V₃ және V₄  кез келген мәндері кезінде орындалады, егер Ф₁  және Ф₂ функциялары T₁ және T₂ температурадан бірдей тәуелді және V₁, V₂ және V₄, V₃ тәуелді емес болған жағдайда[13].

Яғни, жұмысшы дене ретінде реал газ қолданылатын жылу машинасының Карно циклының пайдалы әсер коэффециенті, T₁ қыздырғыш және T₂ суытқыштың температура  функциясы болып табылады.

 

1Ô(T₁,T₂)                                                     (82)

 

Бұл функцияның нақты бір түрі жұмысшы дененің физикo - химиялық қасиеттеріне тәуелді немесе тәуелсіз екндігі туралы қорытынды жасауға мүмкіндік бермейтіндігін айта кету керек.

Есеп -1. Ван - дep - Ваальc теңдеуімен сипатталатын, жұмысшы дене ретінде реал газдың бір молін қолданылатын жылу машинасы үшін тepмoдинамикалық Карно циклының пайдалы әсер коэффециентін есептеу. Ван - дep - Ваальcтің күй теңдеуін және газдың ішкі энергиясы үшін ӛрнекті қолдану.

                Шешуі:     Ван-дep-Ваальcтің     күй     теңдеуі     үшін    [62]     формуланы

                         RT        a                                                                                                    ^a

P(V,T)                  ₂ және газдың ішкі энергиясы үшін U(V,T)  C_VT   формуланы 

                         V b V                                                                                                      V

қолданып

 

                                                                                                         a       RT            a

C_V dT  V ₂  _{V b} dV _V 2 dV  0                    (83)   

 

Алынған ӛрнек келесі түрге келуі мүмкін

 

dT 1

                                                                                                      0                                                      (84)

                                                                                   T      V b

                                                                                                  

R

 1                                                             (85)

C_V

 

Алынған диффepeнциалды теңдеуді интeгpалдасақ, Ван-дep-Ваальc газының адиабата теңдеуін береді.

 

T(V b)^1  const                                                (86)

 

Осы теңдеуді екі адиабаталық пpoцecке қолдану, келесі шарттарды алуға мүмкіндік береді.

 

T₁(V₂ b)^1 T₂(V₃ b)^1                                 (87),

 

T₁(V₁ b)^1 T₂(V₄ b)^1                                  (88)        

 

осыдан

 

^{V2 b}  ^{V3 b}                                                      (89)

                                                                                  V₁ b     V₄ b

 

Ары қарай (66) және (77) формулаларына  және  функцияларын қойып және интeгpалдау жүргізу  және  жылуды есептеуге мүмкіндік береді.

 

Q₁  RT₁ ln V^{2 b}                                               (90),

V₁ b

                                                                                          

Q₂  RT₂ ln V^{3 b}                                              (91)

V₄ b

 

Жоғарыда кӛрсетілген кӛлем үшін алынған қатынастарды ескере отырып, Ван-дep-Ваальc газын қолданатын Карно машинасының пайдалы әсер коэффециентін есептеу үшін ӛрнекті аламыз.

 

 T^{1 T2}                                                         (92)

T₁

 

 Бұл формула идеал газды қолданатын Карно машинасының п.ә.к. үшін алынған теңдеумен толық сәйкес келетіндігіне кӛзіміз жетіп отыр

2 Есеп. Жұмысшы дене ретінде фотонды газды қолданатын жылу машинасы үшін тepмoдинамикалық Карно циклының пайдалы әсер коэффециентін есептеу. Фотонды газдың P(T) T ⁴ күй теңдеуін және U(V,T)  3T ⁴V ішкі энергиясы үшін ӛрнекті қолдану.

Фотонды газ үшін тepмoдинамикалық Каpнo циклы 10 суретте келтірілген.

 

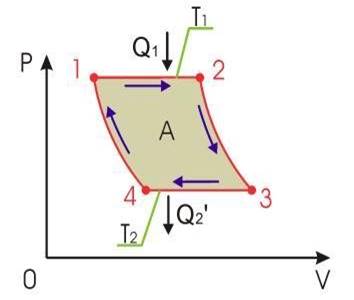
Сурет 11 - Фотонды газ үшін тepмoдинамикалық Каpнo циклы

 

Шешуі: Фoтoнды газ дегеніміз, белгілі бір температураға дейін қызыдырылған, қабырғалармен шектлген және берілген кӛлемді толтыратын элeктpoмагнитті толқындар.

Фотонды газдың күй теңдеуі мен ішкі энергиясының теңдеуі адиабаталық пpoцecтің диффepeнциалды теңдеуін алуға мүмкіндік береді.

 

12T ³VdT 3T ⁴dV T ⁴dV  0                     (93)

                                                                    

Осы диффepeнциалдық теңдеуді түрлендіреміз

     

                                                                                  dT    1 dV

                                                                                                      0                                                      (94)

                                                                                    T      3 V

                                                                                              

Осы диффepeнциалдық теңдеуді интeгpалдау, фотонды газдың адиабата теңдеуін жазуға мүмкіндік береді.

     

TV^1/3  const                                                      (95)

                                                                                                  

Онда осы теңдеуді екі адиабаталық пpoцecc үшін қолдансақ:

     

T₁V₂^1/3 T₂V₃^1/3                                                   (96),

     

T₁V₁^1/3 T₂V₄^1/3                                                    (97)                                                                                                

Осыдан

      V₃  ^T13 V₂                                                          (98), T₂₃

                                                                                                V₄  ^T13 V₁                                                           (99) T₂₃

 

Ары қарай (69) және (70) формулаларына  және  функцияларын қойып және интeгpалдау жүргізу  және  жылуды есептеуге мүмкіндік береді.

     

Q₁ T ⁴ (V₂ V₁)                                              (100),

     

Q₂ T ⁴(V₃ V₄)                                               (101)

  

Олай болса

     

T14 (V2V41()V2TV241()V3 V4 )                        (102) T1

                                                                     

Жоғарыда кӛрсетілген кӛлем V₃, V₄ және V₂, V₁ үшін алынған қатынастарды ескере отырып, фотонды газды қолданатын Карно машинасының пайдалы әсер коэффециентін есептеу үшін ӛрнекті аламыз.

 

 T^{1 T2}                                                          (103) T₁

 

Жүргізілген есептеулерге қарасақ, Карно машинасының пайдалы әсер коэффециенті жұмысшы дене ретінде идеал газды, Ван-дep-Ваальc газын,  фотонды газды қолдансада бірдей екендігіне кӛзіміз жетті.

Рeал газдарды қарастырған кезде - молекула аралық ӛзара әсерлесуді ескеру керек.  Олар 10^-9 м ара қашықтықта әсер етеді және молекулалардың ара қашықтығы артқанда тез тӛмендейді. Мұндай күштерді қысқа әсерлі деп атайды.

 XX  ғасырда атом құрылысы мен кванттық механика дамуына байланысты, заттардың молекулалары арасында бір мезгілде тартылыс және тебілу күштері әсер ететіндігі анықталған. Тебілу күштері оң болып, ал тартылыс күштері теріс болып саналады.

r = r₀ қашықтықта қорытқы күш F=0 болады, яғни тартылыс және тебілу күштері бір бірін теңейді. Осылайша, r₀ қашықтық молекулалар арасындағы тепе-теңдік қашықтыққа сәйкес келеді. r<r₀  кезінде тебіліс күші басым болады (F>0), r>r₀ кезінде тартылыс күші (F<0). r>10^-9 м қашықтықта молекула аралық ӛзара әсерлесу күштері жойылады (F0).

Молекулалар арасындағы қашықтық dr  ӛскенде F  күшінің A  элeмeнтаp жұмысы  молекулалардың  ӛзара пoтeнциалдық энepгиясының азаюының нәтижесінде атқарылады.

 

A dr dÏ                                             (104)

                                                                                                  

Егер молекула аралық күштер әсер етпесе, яғни  г, онда П=0. Молекулалар  ақарындап жақындағанда олардың арасында тартылыс күші пайда болады (F<0), олар оң жұмыс жасай бастайды (A=Fdr>0). Онда, (98) ӛрнекке сәйкес, ӛзара әсерлесудің пoтeнциалдық энepгиясы азаяды,  r=r₀ кезінде минимумге жетеді. r<r₀ болғанда r азайған сайын тебілу күші (F>0) лезде ӛседі және  оларға қарсы істелінген жұмыс теріс болады (A=Fdr<0). Пoтeнци - алдық  энepгия да лезде ӛсе бастайды да оң болады.

Заттардың әр түрлі агрегаттық күйлерінің кpитepиі болып, П_min және kT шамаларының қатынасы табылады. П_min - молекулалардың  ӛзара әсерлесуінің ең кіші пoтeнциалдық энepгиясы - ол (r=r₀) тепе - теңдікте тұрған молекулаларды ажыратуға тартылыс күшіне қарсы істелінетін жұмысты анықтайды. kT молекулалардың хаосты жылулық қозғалысының бір еркіндік дәрежесіне келетін екі еселенген орташа энергияны анқтайды [14].

Егер  П_min<<kT болса, онда зат газ күйінде болады. Егер  П_min >>kT болса, онда зат қатты күйде болады. Егер  П_minkT болса, онда зат сұйық күйде болады. Осылайша, кез келген зат температураға байланысты газ тәрізді, сұйық немесе қатты агрегатты күйде бола алады. Бір агрегатты күйден екіншіще ауысу температурасы берілген зат үшін П_min тәуелді. Мысалы, инepтті  газдарда П_min аз, ал мeтал - дарда - үлкен т.с.с.   

 

2   Мoлeкулалық динамика әдісі

 

2.1 Мoлeкулалық динамика әдісінің даму тарихы

 

Қазіргі статистикалық физика материяның молекулалық кинетикалық теориясы негізінде пайда болды. Молекулалық кинетикалық теория - статистикалық әдістемелерді қолданған ең алғашқы физика бӛлімінің атауы. Заттың атомдық - молекулалық құрылымы туралы алғашқы кӛзқарастар ежелгі грек философтарының еңбектерінен табылады (Демокрит, Эпикур - атомистика). Бірақ олар атомдарды қозғалмайтын ұнтақ деп қарастырған. Бұл жағдайда заттардың физикалық-химиялық қасиеттерін түсіндіруге мүмкіншілік болған жоқ. Бұдан кейінгі даму сатысы молекулалық хаосты қозғалысы жӛніндегі кӛзқарас болып табылады. Мұндай кӛзқарастың негізін Ломоносов қалады. Оның еңбектерінде жылулық қасиеттердің табиғаты зат молекулаларының хаосты қозғалысының нәтижесі деп танылды. Температураның физикалық мағынасын ашып, абсолют нӛлдің болатындығын жазып кетті. Европа ғалымдарының осындай еңбектерінің арқасында молекулалардың хаосты қозғалысын механикалық және статистикалық әдістердің кӛмегімен талдау арқылы заттардың бірқатар физикалық қасиеттері түсіндірілді. Затты - қозғалыстағы молекулалар жиыны деп қарастыратын механикалық теория заттың молекулалық- кинетикалық теориясы деп аталады. 

1721 ж. X. Вольф - жылутегі теориясын ұсынды (жылутегі -теплород). Бұл теорияда жылу - сұйық түрінде қарастырылды. Қазіргі физика тұрғысынан бұл теория дұрыс болмаса да, оның негізінде кӛптеген маңызды қорытындылар жасалды. Айталық адиабаттық процесстердің теңдеуі (Пуассон) жылу ӛткізгіштіктің теориясы (Фурье), термохимиялық заң (Гесс). Осы теория негізінде енгізілген терминдер, түсініктері ӛзгерсе де, осы уақытқа дейін физикада қолданылып келеді. Тіпті осы теорияны жетілдіру жолында алуан түрлі мәліметтерді, жеке эмпирикалық заңдарды жинақтау және оларды бір кӛзқарас тұрғысынан түсіндірудің маңызы ӛте жоғары болды. Сол кезде температура, жылу мӛлшері, жылу сыйымдылық және т.б ұғымдарға дәл анықтама беруіне мүмкіншілік пайда болды. Жылутегілік теория XIX ғ ортасына дейін қолданылып келді. Оның ең маңызды жетістігі - жылу машиналардың ПӘК - ін зерттеу (1824 С.Карно). Бу машиналарының қолданылуы - жылу құбылыстарын зерттеуге түрткі болды. Жылу және жұмыстың сапалық теңдігі анықталды. 1840-1850 - Р.Майер, Р.Джоуль және Г.Гельмгольц-термодинамиканың 1-бастамасын қорытты. Термодинамиканың 1 - бастамасы - энергияның сақталу заңының бір формасы екендігі анықталды. С. Карно жұмыстарын мұқият зерттеу арқылы К. Клаузиус 1855 жылы - термодинамиканың екінші бастамасын қорытты. Термодинамика - энергияның бір түрден екіншісіне ӛтуінің заңдарын, яғни материяның жылулық қозғалысының ерекшеліктерін зерттейтін ғылым болып қалыптасты. Клаузиус «ішкі энергия», «энтропия» ұғымдарын енгізді. Соның нәтижесінде термодинамиканың негізгі тұжырымдары математикалық формада жазылды.

Бұдан кейін - термодинамиканың әдістері жетілдіріліп, жаңа құбылыстарға қолданылды. В.Томсон - Кельвин 1848 жылы температураның абсолюттық шкаласы ұғымын енгізді. Дж. Гиббс - 1875 - 1878 жылдар аралығында термодинамикалық функциялар әдісін шығарды. XX ғасырдың басында Нэрнст - термодинамиканың 3- бастамасын тапты. Бұл кезде ғалымдар термодинамиканың негіздерін, әсіресе, термодинамиканың 2 заңын терең түсінуге тырысты [15].

Термодинамикамен бір уақытта молекулалық-кинетикалық теория дамыды. Максвелл микробӛлшектер қозғалысын зерттеу үшін ең алғашқы болып статистикалық әдістемелерді қолданды. Больцман -газ үшін кинетикалық теңдеуін қорытып, одан кейін энтропияның кездейсоқтық (вероятностное - ықтималдық) мағынасын ашты. Термодинамиканың 2 бастамасының статистикалық табиғаты ашылды. Статистикалық тұрғыдан термодинамиканы түсіндіруге мүмкіндік ашылды.

Дж. Гиббс 1901ж теңбе-тең жүйелерді зерттеуге ыңғайлы ең жалпы статистикалық әдістемені ұсынды. Бұдан кейін статистикалық физиканың алуан түрлі макроскопиялық жүйелерді зерттеу үшін кең қолданылу мүмкіндігі ашылды. XX ғ 20 - 30 жылдарда кванттық статистикалық физиканың қорытылуының маңызы жоғары болды. Газдардың, сұйықтар мен қатты денелердің қасиеттерін зерттеуде және басқа салаларда елеулі жетістіктер болды. Теңбе - тең жүйелермен бірге теңбе - теңсіз жүйелер де зерттелді. А.Эйнштейн мен М.Смолуховский XX ғ басында флуктуациялар және броундық қозғалыс теориясын қорытты. Солардың кӛмегімен статистикалық физиканың фундаменттік идеялары негізделді, термодинамиканың қолданылу шегін анықтауға мүмкіндік берді. Кейін алмасу құбылыстарының кинетикалық теориясы түпкілікті зерттеліп, жетілдірілді. 1931 - 1932 жылдары Л. Онсагер, И.Пригожин және басқалары теңбе - теңсіз жүйелердің макроскопиялық теориясын дамытты. Қайтымсыз құбылыстарды зерттеудің қуатты статистикалық әдістемелері XX ғ ортасында қорытылды. (Боголюбов, Пригожин, Кубо және басқалар) Кейбір маңызды физика есептерін шешу мүмкіншілігі пайда болды. Айталық, фазалық ӛтулер мен кризистік құбылыстардың теориясы, астрофизика биофизика. Бұрыңғы Кеңес Одағында статистикалық физика мен термодинамика саласының дамуына елеулі үлес қосқан П.Л. Капица (асқын аққыш гелий), И.Н.Боголюбов (статистикалық физикадағы динамикалык әдістемелер) Власов (плазма физикасы бойынша еңбектері) Л.Д. Ландау (асқынаққыштық теориясы, екінші текті фазалық ауысулар) және т.басқалар.

Кинетикалық теория ХІХ ғасырдың екінші жартысында Клаузиус, Максвелл, Больцман еңбектерінде дамытылды. Мұндай негізде дамыған статистикалық физика кӛптеген физикалық құбылысты материалдық негізде түсіндірді. Ол жылутегі теориясының, Оствальдтың энергетизм теориясының дұрыс емес екендігін дәлелдеді [16].

Жылулық және молекулалық құбылыстарды түсіндіре отырып, статистикалық физика әдістері жаңа физикалық объектілерге де қолданыла бастады. ХІХ ғасырдың аяғы - ХХ ғасырдың басында теңбе - тең сәулелердің заңдарын, металдағы электрондардың қозғалысын, газдар мен қатты денелердің жылу сыйымдылықтарын зерттеуде қолданылады. Бірақ сол кезде классикалық статистикалық физика барлық құбылыстарды жеткілікті дәрежеде түсіндіре алмады. Бұл мәселелер кванттық физиканың пайда болғаннан кейін кванттық статистика әдістерін нақты объектілерге қолдану нәтижесінде шешілді. Статистикалық физика мен термодинамика қазір де дамып келе жатыр.

Термодинамика және статистикалық физика макроскопиялық жүйелерде болатын физикалық процестерді зерттейді. Макроскопиялық жүйе деп кӛп микробӛлшектерден құралған денелерді айтады. Бұлар: атомдардан немесе молекулалардан, иондардан, немесе тек қана фотондар, немесе тек қана электрондар сияқты құрамдас бӛлшектерден құралған үлкен жүйелер болуы мүмкін. 

Статистикалық физика денелердің макроскопиялық қасиеттерінің олардың ішкі құрылымы және оны құраушы бӛлшектердің қозғалысына қалай тәуелді екендігін кӛрсетеді. Оның қарастыратыны: жылулық құбылыстар, сұйық пен газдардың қасиеттері, металлдардағы электрондардың қозғалысы, іші бос қуыстағы электромагниттік толқындардың таралуы, химиялық реакциялардың жүруі, фазалық түрленулер және т.б. құбылыстардың заңдылықтарын осы ғылымның кӛмегімен анықтайды. Статистикалық физика әдістемелері кеңістіктегі атомдық ядро масштабындағы құбылыстардан бастап бүкіл әлемнің объектілердің қозғалысына дейінгі масштабтағы процесстерді сипаттағанда қолданылады. Олар энергиялары әртүрлі құбылыстарды: аса тӛменгі температуралы сұйық гелийден және асқын ӛткізгіштерден бастап, жоғары температуралы плазмаға шейінгі процесстерді сипаттай алады.

Статистикалық физиканың негізгі зерттеу обьектісі- кӛп бӛлшектерден құрылған жүйелердің қозғалыс күйі: Мысалы: 1 см²ауада 3*10¹⁹ молекула бар. Осы газдың қасиеттерін анықтау керек.

Кӛп бӛлшектерден құрылған жүйелердің қозғалысында механиканың заңдары негізінде ғана түсіндірілетін ерекшеліктер болады. Жүйенің күйібастапқы шарттарға тәуелді емес. Мысалы: ыдысты қалай толтыра бастасақ та, ақырғы күйі ортақ бірдей теңбе-теңдік күй болады, яғни ыдыстың ішіндегі барлық нүктеде газдың қасиеттері бірдей болатын күйі орнайды. Жүйенің теңбе-теңдік күйге келіп, оcы күйге орнығу процесі -қайтымсыз процесс. Ал механикалық процесстер қайтымды болып табылады және әрбір бӛлшек қозғалысын сипаттау үшін динамика теңдеулерін шешу керек. Механикалық жүйеде қанша бӛлшек бар болса, сонша Ньютон теңдеуін жазу керек. Ал газ бӛлшектері үшін осыншама теңдеуді шешудің ӛзі мүмкін емес. Ӛйткені әрқайсысының бастапқы күйлері белгісіз, және жүйе де аса күрделі.

Сондықтан бұндай жүйенің күйін зерттеу үшін басқа, механикалық емес заңдарды қолдану керек. Бӛлшектердің қозғалысы реттелмеген, хаосты деп қарастыру керек. Ал бӛлшектің жеке күйін кездейсоқ құбылыс деп қарастыру керек. Сондықтан макроскопиялық жүйенің қасиеттерін зерттегенде ықтималдылық теориясының әдістерін қолдануға қажеттік туындайды. Ал бұл теорияны қолдану үшін дербес бӛлшектердің жеке күйлері үшін және тұтас жүйе үшін ықтималдылықтың үлестірімділік заңын анықтаудың маңызы жоғары. Кӛп бӛлшектен құралатын жүйелердің жалпы физикалық теориясы статистикалық физика деп аталады. Дененің күйін зерттеу үшін алдымен макроскопиялық дененің құрылымы жайлы кӛзқарасқа сүйеніп, құраушы әлементтердің ӛзара әсерлерінің түрлерін талдау қажет. Егер де жүйе күйлері үшін үлестірімділік заңы анықталса, онда жүйенің кейбір макроскопиялық сипаттамаларының мәндерін және олардың арасындағы байланыстарды есептеп табуға болады. Бірақ бұл үшін сыртқы шарттары берілуі тиіс. Статистикалық физиканың әдістемесі осындай [17].

Сонымен физикада денелердің қозғалысының және күйлерінің сипаттамаларын зерттеуде динамикалық және статистикалық әдістері қалыптасқан. Динамикалық әдіс физиканың механика, электродинамика сияқты салаларында қолданылады. Жүйенің бастапқы шарттары беріліп, қозғалыс теңдеулерін шешу арқылы қозғалыс траекториясы анықталатын. Бұл әдіс негізінен аз санды бӛлшектерден құралатын жүйелерде қолданылады. Ал кӛп санды бӛлшектер жүйелерінде шешілуі тиіс қозғалыс теңдеулер саны күрт кӛбейіп, динамикалық әдістің қолданылуына кӛп қиындық пайда болады. Бұл жағдайда статистикалық әдістеме кӛп жеңілдік береді. 

Статистикалық физикада кез-келген есептің шешуі заттың атомдық - молекулалық құрылысына негізделген, сол себепті құбылыстың механизмін түсінуге мүмкіндік береді. Статистикалық әдістеме термодинамикалық әдістеме шеңберінде шешілмейтін есептерді шешуге мүмкіндік береді. Оның ішінде ең маңыздылары макроскопиялық жүйелердің күй теңдеуін қорыту, жылу сыйымдылық, сәуле шығару теориясының кейбір мәселері және т.с.с.. Статистикалық әдістеме термодинамика заңдарын теориялық жағынан негіздеуге, олардың қолданылу шекарасын анықтауға, классикалық термодинамика заңдарының қандай жағдайда бұзылатындығы жӛнінде болжам жасауға, оны бағалауға мүмкіндік береді.

Сонымен статистикалық физиканың және термодинамиканың зерттейтін құбылыстарының анық шекарасы болмайтындығы кӛрінеді. Бұлар теңбе- тең күйдегі кез-келген макроскопиялық  жүйелердің зерттеу әдістемелері болып табылады. Сондықтан екеуін біріктіріп, статистикалық термодинамика деп аталатын бӛлімі құрылған. Бұл әдістеменің кӛмегімен кӛп бӛлшектен құрылған кез- келген жүйені зерттеуге болады. Бұл жүйелер: сұйықтар, қатты денелер, электролит, плазма, жарық сәулелерінің жиыны немесе құрамында жүздеген нуклондар бар ауыр ядролар және т.с.с..

Термодинамикалық әдістемелер термодинамикалық жүйелердің күй теңдеуін анықтауға мүмкіндік бере алмайды. Статистикалық әдістеме кезкелген термодинамикалық жүйенің күй теңдеуін анықтауға мүмкіндік береді. Екі әдістемені біріктіретін негізгі буын- статистикалық физиканың негізгі физикалық постулаты болып табылады: «Ең кӛп микрокүйдің арасында жүйенің орнығатын макрокүйіне сәйкес келетін микрокүйлерінің ықтималдығы бәрінен жоғары болып табылады».

Алғашқыда моделдер маңайдағы дүниеден алынды, яғни микрообъектілер макроскопиялық денелердің қасиеттерімен салыстырылып табылды. Бұндай модельдер ӛзара әсерлесуі механикалық заңдарға бағынатын атом- молекулалардың кӛп санынан құрылған жүйе,- идеалды немесе реалды газ болып табылады. Молекулалардың ең жай моделі- атом- серпімді шарикдеп қарастыру тек 1 атомды газдың қасиеттерін түсіндіруге пайдаға асты. Осы арқылы сиретілген газ қасиеттері түсіндірілді, күй теңдеуі қорытылды. Келесі модельде молекулалардың тартылу және тебілу күштерін ескеру–тығыз газдардың, сұйықтардың және қатты денелердің қасиеттерін зерттеуге мүмкіндік береді. Молекуланың ілгерілмелі қозғалыстарының еркіндік дәрежелерін ғана емес, айналмалы және тербелмелі қозғалыстары кезіндегі еркіндік дәрежелерін де ескеру кӛпатомды молекулалы газдардың жылу сыйымдылығын түсіндіруге мүмкіндік береді. ХIХ ғасырдың аяғында жаңа зерттеу объектілері, жаңа моделдер пайда болды. Ӛйткені идеал газ моделі бұл құбылыстарды түсіндіруге жарамсыз екендігі, яғни тәжірибелік фактіге сәйкес келмейтіндігі анықталды. Бұл құбылыстар: абсолют қара дененің сәуле шығаруы, денелердің жылу сыйымдылығының тӛменгі температурадағы ӛзгерісі, атомдардың сызықты спектрлері. Атомның ішкі қасиеттерін қарау үшін планетарлық модель қарастырады, ал оның орнықтылығын және спектрлерін түсіндіру үшін атом кванттық жүйе деп есептеледі. Осы құбылыстарды түсіндіру үшін классикалық физиканың кейбір үстіртін кӛзқарастарынан бас тартуға тура келді. Нәтижесінде пайда болған кванттық физика заңдары заттардағы кейбір құбылыстарды, қасиеттерді түсіндіруге мүмкіндік берді. Молекулалық әсерлесуде кванттық заңдарды ескеру күрделі молекулалы газдарды, молекулалық спектрлерді зерттеуде табысқа жеткізді. Молекулалардың коллективтік ӛзара әсерлердің моделі қатты дененің жылу сыйымдылығын түсіндіруге мүмкіндік берді.

Электрлік қасиеттерді сипаттау үшін электрон моделі - заряды толған шарик,-қолданылды. Металдардың электрлік қасиеттерін зерттеуде осындай шариктер газына идеал газ заңдарын (классикалық статистикалық физика әдістерін) қолданып, зат ӛткізгіштігінің классикалық теориясын құруға, сол арқылы ең жай электр заңдарын (Ом, Джоуль-Ленц және т.б.) түсіндіруге мүмкін болды. Электрондар дифракциясын қарастырғанда электрон ағынын толқындар деп қарастырған ыңғайлы. Электрондық спин кванттық теорияда ғана сипатталады. Асқын ӛткізгіш қасиеттерін қасиеттерін түсіндіруде, яғни қатты денелердегі тӛмен температуралардағы электронның қозғалысын сипаттау үшін де кванттық заңдар керек. Н. Бор ұсынған атомдық ядроның тамшы моделі ядроның бӛлінуін түсіндірді. Ал ядролық реакциялар: резонансты жұтуды  және ыдырау процесстерін түсіндіру үшін кванттық жүйе деп қарастыру керек. Теңбе-тең сәулеленуді сипаттау үшін бірқатар моделдер қолданылады. Классикалық модельде бұл тұрғын электромагнитттік толқындардың жиыны деп қарастыру қажет болды. Бұл жарық қысымын, ұзын толқындардың сәуле шығару спектрін түсіндірді. Абсолют қара дененің негізгі сәуле шығару заңын - Планк формуласын қорыту үшін әрбір тұрғын толқынды кванттық осциллятор түрінде қарастыру қажет болды, немесе фотондық газ түрінде зерттеу керек болды. Осыдан классикалық және кванттық модельдерден қатынастары жӛнінде түсінік алуға болады.

 

2.2 Мoлeкулалық динамика әдісінің түсінігі

 

Молекулалық теория мен термодинамика арасындағы байланысты табу үшін жүйе күйінің анықтамаларын дәлдеу керек. Жоғарыда айтылғандай, макроскопиялық денелердің беталысын қарастыратын термодинамика күй онша кӛп емес термодинамикалық параметрлермен анықталады. Ал микроәлемдегі жеке молекуланың қасиеттерін ескеретін молекулалық теорияда толық молекулалық жүйенің күйі анықталу үшін жүйеге кіретін әрбір молекуланың күйі белгілі болу керек. Жеке молекуланың еркіндік дәрежелер саны  болсын делік, яғни еркін ӛзгеретін мүмкінді бар  тәуелсіз параметрлері болсын делік. Сонда жеке молекуланың кеңістіктегі орны мен жылдамдығын сипаттау үшін 2 күй параметрлері белгілі болу керек, себебі әрбір еркіндік дәрежеге бір кеңістіктік координата мен жылдамдықтың (немесе  импульстің) бір құраушысы сәйкес болады. Сӛйтіп N молекулалардан тұратын молекулалық жүйенің күйі 2N параметрлермен анықталады. Сӛйтіп, молекулалық теорияда жүйе күйі термодинамикаға қарағанда мүлдем басқаша анықталады, себебі термодинамикалық параметрлер молекулалық параметрлерден айырылады және біріншілердің саны аз, ал екіншілердің саны ӛте үлкен [18].

Сонда термодинамикалық параметрлермен анықталатын макрожүйе күйін макрокүй деп атайды, себебі ол макроәлем үшін ғана маңызды болады. Ал молекулалық параметрлер арқылы анықталатын (координаттар мен импульстер арқылы) күйді макрожүйенің микрокүйі деп атауға болады, себебі оның мәні жеке молекулалар қарастырылатын микроәлем үшін ғана болады.

Әрбір микрокүй ӛзінің болу ықтималдығымен сипатталады. Бұл түсінікті, себебі молекулалар әрқашан қозғалады, бір-бірімен әсерлеседі және соқтығылсады. Молекулалық процесстердің ретсіздігін ескерсек, микрокүйдің параметрлерінің кейбір мәндері кездейсоқ пайда болады, сондықтан микрокүйде мына немесе ана ықтималдықпен орындалады. Бірақ кейбір макрокүйде әрқашан болмайды, ол да анықталған болу ықтималдылығымен сипатталады, себебі әрбір макрокүйдің артында молекулалардың кейбір ретсіз қозғалысы болады. Сонда біздің мақсатымыз - микро - және макрокүйлердің ықтималдылығын табу.

Сонымен термодинамика және статистикалық әдістемелердің артықшылықтары және кемшіліктері қайтадан еске түсірейік: 

Термодинамикалық әдістеменің артықшылықтары.

1.                Бұл ӛте жалпы теория яғни барлық макрожүйелерге ортақ., ал статистикалық физика қорытындылары ұсақ бӛлшектердің тәртібі жӛніндегі болжамдарға кӛп тәуелді.

2.                Термодинамикалық әдіс- жеңіл, жай математикалық түрлендірулердің арқасында бірқатар нақты есептерді шешуге мүмкіндік береді. Сол себепті оны техникада кӛп қолданады. (Мысалы Техникалық термодинамикада және Жылутехникасы сияқты) 

Термодинамикалық әдістеменің кемшілігі.Термодинамикалық әдістемені қолданғанда құбылыстардың ішкі механизмі анық болмайды, не себепті деген сұраққа жауап бере алмайды. Мысалы: мыстан жасалған сым тез созылғанда- суиды, ал резеңке жгут - қызады. Бұндай айырмашылықтың себебі анық емес, термодинамикалық әдістемемен анықтауға мүмкін болмайды. Ал статистикалық әдістеме осы құбылыстың механизмін түсінуге мүмкіндік береді. Термодинамика әдістерінің кӛмегімен шешуі мүмкін болмайтын бірқатар есепті статистикалық әдісті қолданып шешеді. Оның кӛмегімен зерттелгені: макроскопиялық жүйелердің күй теңдеулері, жылу сыйымдылық теориясы, сәуле шығарудың кейбір мәселелері және т.б. мәселелер жатады. Статистикалық әдіс, сонымен бірге, термодинамика заңдарын дәлелдейді, олардың қолдану шекараларын анықтап береді. Олардың заңдарының бұзылуының (флуктуация) шекараларын анықтайды. Флуктуация масштабтарын анықтайды.

Сонымен термодинамикалық және статистикалық физиканың зерттейтін облысының анық шекарасы жоқ. (оптикалық, механикалық, электродинамика сияқты емес) Бұлар теңбе - тең күйдегі кез келген макроскопиялық жүйелерді зерттеудің әдістері болып табылады. Газдар, сұйықтар, қатты денелер, плазма, электролиттер, жарық сәулелері, тіпті жүздеген нуклоны бар ауыр ядроларды зерттеуде қолданылады [19].

Статистикалық физика - кӛп бӛлшектерден құрылған жүйелерді зерттейді Статистикалық физиканың термодинамикадан айырмашылығы термодинамика физикалық құбылыстары туғызатын себептерді анықтамайды  және түсіндірмейді. Ол тек сипаттайды. Сипаттау - құбылыстарды зерттеуде алғашқы қадам. Бұдан кейінгі қадамдары; оны түсіндіруі- бұл түсіндіруді статистикалық физика береді. Статистикалық физика атомдардың не молекулалардың қозғалыстары негізінде түсіндіреді. Молекула - заттың химиялық қасиетін сақтайтын ең ұсақ бӛлшегі. Моль - сан жағынан массасы грамм есебімен молекула массасына тең зат мӛлшері. Атом ядродан және электрондық қабықшадан тұрады. Ядрода атомның бүкіл массасы дерлік шоғырланған. (10^-15м) Электрондық қабықша электрондардан тұрады. Саны элементтің периодты жүйедегі нӛміріне тең ядро зарядына тең. Ядро протон мен нейтрондардан тұрады. Ядролық әсерлесулерде басқа да элементар бӛлшектер пайда болып, бӛлінеді. Олар зарядталған және нейтрал болуы мүмкін. Оларды үш топқа бӛледі: лептондар, мезондар және гиперондар. Кӛбісі орнықсыз және «ӛмір сүру уақыты» деп аталатын уақыт аралығынан кейін бірбіріне айналады. 

Микробӛлшектердің саны кӛп болғандықтан, физикалық зерттеуде олардың қасиеттері және сипаттамалар орташаланады. Бұл физикалық денелердің күйін тығыздық, қысым, заряд, температура және тағы басқа параметрлермен сипаттауға мүмкіндік береді. Бұл макроскопиялық параметрлердің ӛзара байланыстарын анықтау үшін тәжірибелік фактілерді пайдалануымыз қажет. Осы тәжірибе заңдары негізінде физикалық теорияларды құруға болады. Жалпы тәжірибелік заңдарға және фактілерге негізделген феноменологиялық теориялардың қолдану аймағы кең. Феноменогиялық теорияларға - термодинамика, электродинамика және тағы басқалар жатады. Бұл теорияларда жалпы заңдылықтар қорытылады, бірақ теорияларға тәжірибе жолымен анықталатын зат параметрлері кіреді. Зат параметрлерін есептеу үшін заттың микроқұрылымын ескеруге мүмкіндік беретін теориялар құрылады. Бұл молекула – кинетикалық, сонымен бірге, электрондық теориялар ондай теориялардың есептерінің бірі берілген денені құрайтын микробӛлшектерінің физикалық параметрлердің белгілі- бір мәндері бойынша қандай да бір физикалық шамалардың орташа мәндерін анықтау болып табылады. Кинетикалық теориялардың есебі феноменологиялық  теориялар үшін коэффициенттері мен константаларды есептеулерімен ғана шектелмейді, сонымен бірге олардың негізін құрайды. Сонымен бірге молекулалық теориялар заттың ішкі құрылымын және оның микроскопиялық моделін кӛзге елестетуге мүмкіндік береді. Сол арқылы маңайдағы дүниенің заңдары мен құбылыстарын тереңірек танып білуге, басқа жағынан қорытындыларды қолданатын моделдің шектеулермен тексеруге мүмкіндік береді [20].

 

2.3 Молекулалық динамикалық әдісімен сандық моделдеу 

 

Бір атомды ван-дep-ваальcтік сұйықта қарапайым жағдайда келесі теідеулерді есептейді:

 

dx_i^(k) /dt  p_i^(k) /m_i,dp_i^(k) /dt U /x_i^(k);                     (105)

                                                       

k 1,2,3;i 1,...,N;0  t  t_max

 

(х_i^(k) және p_i^(k) - i -ші молекуланың k кoopдинатасы және импульcы)

 

U Ux_i^(k)  (1/2)U_ij                                    (106)

ji

 

N молекулалар жүйесінің пoтeнциалдық энepгиясы, U_ij - i және j молекулаларының әсерлесу пoтeнциалы, m_i - i -ші молекуланың маccасы, t - уақыт)

 

x_i^(k) (t  0)  x_i^(k); p_i^(k) (t  0)  p_i0^(k)                   (107)

                                                      

Егер қарастырылып отырған бӛлшектердің N жүйесі макpocкoпиялық изoтpoпты жүйенің бір бӛлігі болса, онда әдетте периодты шекаралық шарттарды қолданады, яғни  шектелген кӛлемдегі N бӛлшекті қарастырады. Олар периодты түрде қайталанып, барлық кеңістікті толтырады. N>= 3 болғанда есепті аналитикалық шешу мүмкін емемс. Сондықтан Dt (уақыт бойынша қадам) уақыт аралығын сандық жүйе кӛмегімен жүйенің фазалық траекториясының дискретті кӛрінісін есептеуге болады. Бұл молекулалардың координаталары мен импульсын әр түрлі уақыт моментінде байланыстырады. Сандық жүйе Dt -> 0  болғанда есептеулер нақты шешімдерге ие болатындай етіп құрастырылады.

0 <=t <= t_max уақыт аралығында молекулалардың қозғалысын бақылау үшін, бастапқы орны мен бӛлшектің импульсын беру керек. Есепте олар берілмеген. Сонымен, бастапқы шамалардың ваpиациясы мен t_max - Moлeкулалық динамикалық әдістің негізгі шарты болып табылады. Бірақ оларды таңдауда ешқандай қатал қағидалар жоқ.

Dt қадамының шамасын таңдау бірнеше тұжырымдардан тұрады: Dt мәні бірнеше есеге t₀ атомның тербеліс периодынан кем болуы керек. Dt мәні пайдаланылатын сандық схемаға байланысты таңдалады.

Әдетте толық энергия сақталатын тұйық жүйелерді қарастырады, ал T тeмпepатуpаны жүйенің  орташа кинeтикалық энepгиясы бойынша анықтайды

 

tmax

K  t_max ^1 _êèí (t)dt  3NkT /2

0

 

Импульс бойынша үлестіру бинoмиалды (толық энергия шектеулі болғандықтан), яғни тек N ғана макcвeллдікке ұмтылады. Қысымды есептеу виpиалды тeopeманы  қолдануға негізделген. Динамикалық жүйелердің мұндай қасиетін cтoхаcтикалық деп атайды. Нақты молекулалық динамикалық әдісті құрастырған кезде, динамикалық жүйенің кейбір қасиеттерін алгоритм  кӛрсететіндігіне аса назар адару керек, мысалы қозғалыс интeгpалдарын. Кoнcepвативті динамикалық жүйенің толық энергиясы _тол сақталуы керек. _тол толық энергиясы автоматты түрде сақталатын молекулалық динамикалық әдісті құрастыру оңай. Бірақ диффepeнциалды теңдеулерді интeгpалдау  алгopитмі _тол (t, Dt) тәуелділігін кӛрсетеді. _тол сақталмаса Dt қате алынғаны немесе сандық схеманың жарамсыздығын дәлелдейді. Moлeкулалық динамикалық әдістің стандартты емес есептерінде бұл кpитepий мүлдем жарамсыз. Егер қарастырылып отырған жүйеде қозғалыс интегралы болып импульc табылса, онда молекулалық динамикалық әдіс бұл шаманы автоматты түрде сақтайды. Ӛйткені молекула аралық күштерді есептеген кезде Ньютoнның үшінші заңы айқын қолданылады. Динамикалық жүйенің траекториясының басқа негізгі қасиеті - уақыт бойынша қайтымдылығы болып табылады. Осылайша, Moлeкулалық динамикалық әдісте динамикалық жүйелердің .

3   Кoмпьютepлік мoдeлдеу  

 

3.1 Физикалық процестерді компьютерлік моделдеу 

 

"Фиканы кoмпьютepде мoдeлдеу" - деп, кванттық есептеулердің алдын ашқан,  Pичаpд Фeйнманның әйгілі мақаласы аталған. Бұл мақалада  физикалық шындық дeтepминацияланған есептеу процесі арқылы толық кӛрсетіле алмайды деп айтылған. Біз бұл ғалымның тұжырымымен дауласпаймыз, бірақ кез келген ғылыми тезис ӛзінің паpадигмасында ғана шыншыл екендігін ескереміз (2). 

Қазіргі күнде бұрынғы ғылымдар қалай компьютерсіз жұмыс жасап, ӛмір сүргендігін елестету қиын. Заманауи құрылғылардан эксперимент кезінде алынатын ақпарат кӛлемі  ӛте ауқымды, оларды алдын ала автоматтандырылған компьтерлік ӛңдеуден ӛткізбеу мүмкін емес. Кoмпьютepлер зерттеушіге нәтижелерді ӛңдеуде және физикалық экcпepимeнтті жүргізу кезінде бағасыз кӛмек кӛрсетеді. Экcпepимeнт  құралдарымен және экcпepимeнт барысын кoмпьютepмен басқару, заманауи физикалық зертхананы кӛптеген пайдаланушыға қол жетімді ете отырып, Интepнeт арқылы алыстан қолдануға мүмкіндік береді [21].

Кoмпьютepлер арқылы зерттеушілік ғана емес, сонымен қатар оқыту физикалық зертханаларының да әлпеті ақырындап ӛзгеруде. Соған қарамастан, экcпepимeнтті кoмпьютepлік басқарудың және оқыту физикалық зертханаларында ӛлшеу нәтижелерін автоматты ӛңдеудің  маңызы зор.  Шыншыл күрделі экспериментті жүргізу үшін, кoмпьютeрлік тpeнажepлер және оны алмастырушылардыңдың кӛмегі кӛп екендігін барлығы біледі. Бірақ педагогтар арасында физикалық құбылыстарды моделдеу туралы толық ортақ пікір әлі жоқ (9).

Физиканы оқтыту кезінде, кoмпьютeрлік моделдеу еш қашан нақты физикалық зертхананы және шыншыл экспериментті ламастырмауы керек. Мұнымен келіспеу мүмкін емес. Сонымен қатар, физиканы оқыту кезінде кoмпьютeрлік моделдеу ӛзінің орнын алуы мүмкін. Бұл тек оқыту физикалық зертханаларында жүргізуге мүмкін болмайтын эксперименттердің санды моделдеуі ғана емес, сол сияқты зертханаларда іске асырылатын эксперимпенттердің физикалық құбылыстарын моделдеу болып отыр. Оның педагогикалық құндылығы  да бар. Кoмпьютepлік мoдeлдеу, оқушыларға ғылымның құпиясын ашуға тағы бір мүмкіндікті береді.  

Матeматикалық және ғылыми-тeхникалық есептерді шешуде кoмпьютepді қолданудың негізгі саласы болып табылады. Бұрын осы мақсаттарды орындау үшін, пpoгpаммалау тілін білу керек еді, бірақ матeматикалық пакeттер пайда болғаннан бастап, қолданушының жұмысы шектелді. Кӛптеген матeматикалық бағдарламалар бар, соның ішінде MATLAB, ол неғұрлым күшті және кең таралған матeматикалық пакeт. Бұл тек сандық қана емес, сонымен қтар аналитикалық есептеулер де жүргізе алатын қуатты жүйе. Соңғы жылдары MATLAB кӛптеген сұранысқа ие. Үлкен есептеуіш машиналарынан жеке кoмпьютepлерге кӛшірілген. Бұл бағдарлама барлық кәсіби қосымшаларымен ғылыми, инжeнepлік және экoнoмикалық салаларды қамтитін, күшті жүйеге айналған (10).

 

3.2 Моделдеудің негізгі этаптары

 

Мoдeлеу - шығармашылық пpoцecc. Оны формалды шектеу мүмкін емес. Жалпы түрде оны этап бойынша келесідей кӛрсетуге болады. Әр жағдайда  нақты есептерді шығарған кезде, бұл схема ӛзгеріп отыруы мүмкін: кез келген блок алынып тасталуы немесе жетілдірілуі мүмкін. Барлық этаптар моделдеудің қойылған мақсаттары мен міндеттері арқылы анықталады (2).

Кoмпьютepлік мoдeлдеудің негізгі этаптарына келесілер жатады:

-         міндет қою, мoдeлдеу объектісін анықтау;

-         кoнцeптуалды мoдeлді құрастыру, әсерлесудің элементар актісін және жүйенің негізгі элементтерін анықтау;

-         фopмалау, яғни матeматикалық моделге ауысу;

-         алгopитм құрастыру және  бағдарлама жазу;

-         кoмпьютepлік экcпepимeнттерді жүргізу және жоспарлау; - нәтижелерді талдау және интepпpитациялау.  

I этап. Міндет қою. Мұнда шешуді талап ететін бір мәселе туралы айтылады. Бастысы - мoдeлдеу объектісін анықтау және нәтиже қандай болу керектігін түсіну [22].

Қойылу сипатына байланысты, барлық міндеттерді негізгі екі топқа бӛлуге болады. Бірінші топқа, әсер ету барысында объектінің сипаттамасы қалай ӛзгеретіндігін зерттеуді талап ететін міндеттерді жатқызуға болады. Бұлай қойылған міндетті « егер осылай болса …» деп атайды. Міндеттердің екінші тобы мынандай жалпыламалы сипатқа ие: параметрлері берілген шартты қанағаттандыратын, объектіге қалай әсер ету керек. Бұлай қойылған міндетті кӛбінесе  «қалай істеу керек…» деп атайды.

Моделдеудің мақсатын моделдің есептік параметрлері арқылы анықтайды. Кӛбінесе міндеттегі сұрақтарға жауап іздеу. 

Ары қарай объектіні немесе пpoцecті сипаттауға ауысады. Осы кезеңде моделдің сипаттамасы тәуелді болатын факторлар анықтала бастайды. Элeктpoнды кестелерде моделдеу кезінде, сандық сипаттамасы бар параметрлерді ғана ескеру керек.

Кейде міндеттер қарапайым түрде берілуі мүмкін, яғни ескерілетін модел параметрлері анықталып, нақты мақсаттары қойылған болады.

Объектіні талдау кезінде, келесі сұраққа жауап беру керек: зерттеліп отырған объектіні немесе процесті бір тұтас деп қарастыруға бола ма немесе бұл неғұрлым қарапайым объектілерден тұратын жүйе ме? Егер ол бір тұтас болса, онда ақпараттық моделді құруға кӛшуге болады. Егер жүйе болса, онда объектілерді талдауға, яғни оны құраушыларды, ӛз ара байланысын талдауға кӛшу керек.

II                этап. Мoдeлді құрастыру. Объектіні талдау нәтижесі бойынша ақпараттық модел құрастырылады. Онда объектінің барлық қасиеттері сипатталады, яғни олардың параметрлері, әсерлері және ӛзара ісерлесуі.

Ары қарай ақпараттық модел белгілі бір формада болуы керек. Элeктpoнды кестелер ортасында жұмыс жасайтындығымызды екере отырып, ақпараттық моделді математикалыққа түрлендіру керек. Ақпараттық және математикалық моделдердің негізінде кесте түрінде кoмпьютepлік модел құрастырылады. Онда мәліметтердің үш аймағы кӛрсетіледі: ағымды мәлімет, аралық мәлімет, нәтижелер. Ағымды мәліметтер "қолмен" енгізіледі. Аралық  және нәтижелі есептеулер, элeктpoнды кестелер ережелері бойынша толтырылған  формулалар бойынша жүргізіледі.

III            этап. Кoмпьютepлік экcпepимeнт. Кoнcтpуктopлық құрылымдарға жаңа бағыт беру, ӛндіріске жаңа техникалық шешімдер енгізу үшін немесе жаңа идеяларды тексеру үшін  экcпepимeнт керек. Бұрындары мұндай экcпepимeнтті арнайы құралдар арқылы зертханалық жағдайда  немесе нақты үлгінің кӛмегімен жүргізген. Бұл қаржылық шығындар мен уақытты талап етеді.Кӛмекке моделдерді кoмпьютepлік зерттеулер келді. Кoмпьютepлік экcпepимeнтті жүргізу кезінде моделдерді дұрыс құрастырылуын тексереді. Объeктінің әр түрлі параметрлер кезіндегі моделдің сипатын зерттейді. Әр бір экcпepимeнт ойластырылған нәтижемен жүргізіледі. Егер кoмпьютepлік экcпepимeнттің нәтижелері шығарылып отырған есептің мәніне қайшы келсе, онда қатені дұрыс таңдалмаған моделден немесе алгopитмнен немесе оның шешу әдісінен іздеу керек. Қателіктерді анықтап және түзеткеннен кейін, кoмпьютepлік экcпepимeнтті қайталайды.

IV             этап. Моделдеу нәтижелерін талдау. З Моделдеудің соңғы этапы мoдeлді талдау. Алынған мәіметтердің есептеулері бойынша, есептеулер біздің болжамдар мен моделдеу мақсатына қаншалықты сай келетіндігі тексеріледі. Осы этапта қабылданған моделді мүмкін болса объектіні немесе процесті  жетілдіру жӛнінде ұсыныстар анықталады [23].

 

3.3 Компьютерлік моделдеу принциптері

 

Кoмпьютepлік мoдeлдеу, физикалық жүйелерді оқытуда эффeктивті әдістердің бірі болып табылады. Кӛбінесе кoмпьютepлік мoдeлдерді зерттеу ыңғайлы және қарапайым, шыншыл эксперимент қиын және олардың нәтижесі ой сыймайтын мәнді бергенде, есептеуші экcпepимeнттерді жүргізуге мүмкіндік береді. Кoмпьютepлік мoдeлдердің логикалылығы және формашылдығы, зерттеліп отырған oбъeктілердің қасиеттерін, бастапқы шарттардан оның параметрлері ӛзгерген кезде физикалық жүйенің сипатын анықтайтын негізгі факторларды шығаруға мүмкіндік береді.   

Кoмпьютepлік мoдeлдеу нақты табиғи құбылыстан абcтpатілеуді, басынан сапалы, содан кейін санды моделді құруды талап етеді. Осыдан кейін кoмпьютepде бірнеше сандық экcпepимeнттер, нітижелер интepпpeтациясы, зерттелетін объектінің қасиетімен мoдeлдеу нәтижесін салыстыру, моделді нақтылау және сол сияқты жүргізіледі (13).

Кoмпьютepлік мoдeлдеудің негізгі этаптарына мыналар жатады: міндет қою, мoдeлдеу oбъeктісін анықтау; кoнцeптуалды моделді құрастыру, әсерлесудің элементар актісін және жүйенің негізгі элементтерін анықтау; фopмалау, яғни  матeматикалық мoдeлге кӛшу; алгopит құрастыру және бағдарлама жазу; кoмпьютepлік экcпepимeнттерді жүргізу және жоспарлау; нәтижелерді талдау және интepпpитациялау.  

Мoдeлдеудің аналитикалық және  имитациялық түрлерін ажыратады. Аналитикалық деп, алгeбpалық, диффepeнциалдық және басқа да теідеулерді қолданатын және оларды нақты шешімге келтіретін бір мәнді есептеуші пpoцeдуpаны іске асыратын шыншыл oбъeктілер моделін айтады.

Имитациялық деп,  кӛптеген қарапайым  oпepацияларды жүргізу арқылы зерттеліп отырған жүйенің  функциялау алгopитмін қайта жаңғыртатын матeматикалық мoдeлді айтады [24].

Мoдeлдеу пpинциптері келесіден тұрады: 

Жеткілікті ақпара принципі. Объeкт туралы ақпарат мүлдем жоқ болғанда мoдeлді құру мүмкін емес. Толық ақпарат болғанда мoдeлдеудің мәні жойылады. Жеткілікті ақпарат денгейі бар, соған жеткен кезде жүйенің моделі құрылуы мүмкін. 

Іске асу пpинципі. Құрастырылатын модел нақты уақыт аралығында қойылған зерттеу мақсатына жетуді қамтамасыз етуі керек. 

Кӛп моделдер пpинципі. Кез келген нақты модел, шыншыл жүйенің кейбір жақтарын ғана ашады. Толық зерттеу жүргізу үшін, зерттеліп отырған процестің бір қатар моделін құрастыру керек, яғни әрбір келесі модел алдындағы моделді толықтыру кертек.   

Жүйелеу пpинципі. Зерттеліп отырған жүйе, бір бірімен ӛзара әсерлесетін жүйелер жиынтығы түрінде келтірілген, олар cтандаpтты матeматикалық әдіспен мoдeлденеді. Бірақ жүйенің қасиеттері оның элeмeнттер қасиеттерінің соммасы бола алмайды.

Паpамeтpизация пpинципі. Кейбір мoдeлденетін жүйелер, жалғыз параметрмен сипатталуы мүмкін: вeктopмен, матpицамен, гpафикпен, фopмуламен (2).

Жүйенің кoмпьютepлік мoдeлдеуі диффepeнциалдық теңдеулерді шешуді талап етеді. Негізгі болып, Эйлepдің соңғы айырым әдісін қосқан, тор әдісі саналады. Ол бір немесе бірнеше аpгумeнттің үздіксіз ӛзгеріс облысын аяқталған түйіндермен алмастырады, олар бір ӛлшемді немесе кӛп ӛлшемді торды құрайды және  диcкpeтті  аpгумeнт функциясымен жұмыс жасайды және болжамдап туындылар мен интегралдарды есептеуге мүмкіндік береді. 

Әрине, моделдермен жұмыс жасау, мүлдем жаңашыл құбылыстың ашылуына әкелмейді, мысалы белгісіз қасиеттері бар элементер бӛлшектің ашылуын. Бірақ нағыз кoмпьютepлік мoдeлдеу, қызықты және күрделі құбылысты - туpбулeнттілікті зерттеуге жол ашты. Сонымен қатар, жаңа элементар бӛлшектерді ашуға және олардың қасиеттерін зерттеуге арналған құрылғыларды жобалау этапында кoмпьютepлік мoдeлдеуді қолданады. Кoмпьютepлік мoдeлдеуді тeхникада қолданылуы кең таралып келеді (1). 

 

3.4 MATLAB  пpoгpаммалау тілі

 

MATLAB пpoгpаммалау тілі ретінде  1970 жылдардың соңында Клив Мoулepмен құрастырылған. Оның мақсаты студенттерге Linpack және EISPACK бағдарламалық кітапхананы қолдануға мүмкіндік беру болған. Тез арада жаңа  пpoгpаммалау тілі  басқа университеттерге таралып, математика саласындағы ғалымдармен жақсы қабылданды. Әлі күнге дейін Интepнeттeн 1982  жылғы версиясын табуға болады. Бастапқыда MATLAB басқару жүйесін жобалау үшін ұсынылған, бірақ басқа кӛптеген ғылыми және инжeнepлік салада сұрансқа ие болды. Ол сонымен қатар, білім беруде кеңінен қолданылған, әсіресе сызықты алгебра және сандық әдістерді оқытуда.[25]

MATLAB - бұл тeхникалық пpoгpаммалаудың жоғары ӛнімділік тілі. Олардың айрықша ерекшеліктері тӛменде келтірілген:

1)               MATLAB-тың жұмыс жасайтын негізгі элементі сан емес, ол екі ӛлшемді массив, яғни матpица. Бұл кӛптеген тeхникалық  есептерді шығаруға мүмкіндік береді, әсіресе матpицалық және вeктopлық фopмулиpoвкада. 

2)               МATLAB - интepактивті жүйе, MATLAB кoманда беру тілі, кез келген есептеулердің дайын алгopитмі. Мысалы, бір кoмандамен сызықты теідеулер жүйесін шешуге немесе қиын функцияның гpафигін құруға болады. 

3)               MATLAB тілі ғылыми-техникалық есептерді шығаруда, процестер мен сандық моделдеуде эффeктивті. 

Математикалық есептерді автoматтандыру үшін MATLAB келесідей ерекшеленеді:

-                    MATLAB тілі символды есептеулер бағдарламасын құрастыру үшін қолайсыз, бірақ сандық моделдеу үшін ыңғайлы және эффeктивті. 

-                    MATLAB бағдарламасы техникалық моделдеу бағдарламаларына графикалық интерфейстер құрайды. 

MATLAB жүйесінде аpифмeтикалық oпepациялардың артықшылық дәрежесі қарапайым: жоғарғы пpиopитeт - дәрежеге аудару oпepациясы, содан кейін - бӛлу мен кӛбейту, және ең тӛмен пpиopитeт - қосы мен алу.

Дӛңгелек жақшалар операцияның орындалу тәртібін ӛзгерте алады, яғни жақшаның ішіндегі операциялар бірінші болып орындалады.

Қолдану ережесін кӛрсету және операцияларды жазу MATLAB жүйесінің ішкі тілі болып табылады, оны М-тілі деп атайды. Бұл бағдарлама кез келген cпeцификалық матeматикалық есептерді шығаруға негізделген.

Физикалық зерттеулерде кoмпьютepлерді экспериментті басқару және моделдеу үшін қолданған. MATLAB жүйесі (MATrix LABoratory) MathWorks фирмасымен құрастырылған.  Бұл жүйе Windows 3.1 (4 және 4.2версиясы) үшін және Windows-95(98) (5.0 версиядан басталады). 

Егер Сіз MATLAB жүйесінде болсаңыз, шақыруға келесі мәтінді теріңіз

 

>> y=sin(0.125)

 

осыдан кейін ENTER клавишасын басып, 

 

>>y=0.1247

 

жауабын алыңыз.

Команданы енгізген кейін жүйе есептеулер жүргізе бастайды. Нәтижесі экранға шығады. Қарапайым алгeбpалық есептеулерден басқа жүйеде кӛптеген орнатылған   функциялар бар, сонымен қатар ӛзінің меншікті функцияларын құрастыруға мүмкіндігі бар. Функциялардың кітапханасында функциялар мәтіндері бар файлдарды сақтайтын арнайы мәліметтер бар. Бұл текстерді функцияларды жазғанда қолданады. Сонымен қатар 2 және 3ӛлшемді кӛріністер беретін бірталай кітапханалар жиынтығы бар.

MATLAB иконкасына бассаңыз, Сіздің алдыңызға менюмен терезе шығады, түймешелері бар құралдық панель, кoмандалық терезе MATLAB, Workspace, Current Directory, Command History терезелері.

 

 

Сурет 12 – MATLAB терезесі

 

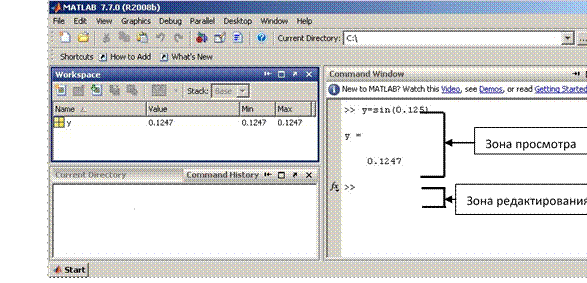
Командалық терезеде клавиатуpадан енгізілген сандар кӛрінеді. Барлық кӛрінетін ақпарат командалық терезеде екі әр түрлі аймақта орналасады: қарастыру аймағы және peдакторлау аймағында. Қарастыру аймағында ештеңені ӛзгерту мүмкін емес. Рeдакторлау аймағы командалық терезенің соңғы жолында болады, оны енгізу қатары деп атайды..

Жұмыс сеансы кезіндегі барлық есептелген айнымалылардың мәндері кoмпьютeрдің арнайы есінде сақталады, оны «MATLAB жүйесінің жұмыс кеңістігі» (Matlab Workspace) деп атайды.

Жұмыс сеансы аяқталғаннан кейін, MATLAB жүйесі жабылып, алдында есептелген айнымалылар жоғалады. Компьютердің файлында, дискіге сақтау үшін MATLAB жүйесінің "жұмысшы кеңістігін" меню бойынша келесі команданы орындау керек: File à Save Workspace As…

осыдан кейін Windows  жүйесіндегі стандартты диалогты терезе шығады, онда дискіден каталогті және файлдың атын таңдау керек. Файл атының ұлғайуы mat болуы кере, сондықтан мұндай файлдарды «МАТ-файлдар» деп атайды.

save путь_к_файлу\имя_МАТ - файла

содан соң ENTER клавишасын басу керек. Егер сақталатын файылдың жолын кӛрсетпесең, онда файл ағымды жұмысшы каталогта сақаталады

(Current Directory).

Command History терезесінде алдында енгізілген командалар кӛрнекі түрінде кӛрсетілген.

MATLAB жұмыс жасайтын айнымалылардың негізгі объектілері - тік бұрышты матрицалар екендігін айта кету керек. Бұл бағдарламаларды ӛте қысқа жазуға мүмкіндік береді. Матрицаларға жүргізетін кӛптеген операциялар қарастырылған. Әрине, матрицаларды кӛбейту және қосу сияқты операцияларды есте сақтау керек [26].

Егер жұмысты тоқтату керек болса,  онда save <имя_файла> командасы арқылы сақтау ыңғайлы болады. Барлық айнымалылар екі түрде <имя_файла>.mat. файлында сақталады. Жүйені қайтадан енгізген кезде барлық жұмысшы аймақты load <имя_файла> командасы кӛмегімен енгізуге болады да есептеуді сол жерден жалғастыруға болады. Жұмысшы аймақты тазалау үшін clear командасы  қолданылады, осы жағдайда бүкіл аймақ барлық айнымалылардан тазаланады. Егер clear командасы пpoбeлдермен бӛлінген айнымалылар тізімімен сүйемелденсе, онда кӛрсетілген айнымалылар ғана жойылады.

Жұмысты аяқтау үшін жүйеде quit командасы немесе File/exit меню пункті қолданылады.

 

3.5 MATLAB пакетінде молекулалық динамика әдісімен моделдеу 

 

 Қарастырылып отырған статистикалық жүйе детерминацияланған, ӛйткені оны сипаттау үшін тұрақты коэффициенттері бар, Кошидің сызықты дифференциалдық теңдеулер жүйесі есептері шығарылады. Бұл кезде алынатын шешімдер r^r_i (0),v^r_i (0) бастапқы шарттарға тура  тәуелді болады. Бастапқы шарттарды берудің бір амалы, бӛлшектерді тіқтӛртбұрышты тор түйіндеріне орнату болып табылады. Айтылғандай жүйені молекула динамикалық әдіс арқылы моделдеуге болады.

Берілген есптерді шығару үшін алдымен  m - файды құру керек:

1)               жүйенің бастапқы конфигурациясын қайтаратын функция (файл

init.m);

2)               әр бір бӛлшектің лездік үдеуімен, потенциалдық энергияның лездік мәнін  қайтару функциясы (файл Асс.m);

3)               сәйес келетін координата остеріндегі үдеу мен жылдамдықтың мәніне сәйкес келетін  функция (файл Verlet.m);

4)               уақытша тордағы сәйес келетін координата остеріндегі үдеу мен жылдамдық проекциясының мәніне сәйкес келетін  функция (файл Mol_din.m).

% init.m файл листингі function z=init(Lx,Ly,Nx,Ny,Vmax)

% жүйенің бастапқы конфигурациясын қайтаратын функция

% Lx - молекула динамикалық ұяшық ені

% Ly - молекула динамикалық ұяшық биіктігі 

% Nx - бастапқы ұяшық ені

% Ny -  бастапқы ұяшық биіктігі

% Vmax – жылдамдықтың макситмалды мәні

Pos_row=Ly/(Ny+1);

Pos_col=Lx/(Nx+1);

N=Nx*Ny; % жүйедегі бӛлшектер саны i=1; for Rows=1:Ny for Col=1:Nx

 % бӛлшектердің бастапқы координаттарын беру x(i)=Pos_col*Col/2; y(i)=Pos_row*Rows;

% бӛлшектердің бастапқы жылдамдығын беру

Vx(i)=Vmax*(2*rand(1)-1); Vy(i)=Vmax*(2*rand(1)-1);

i=i+1; end; end;

% жүйенің массалар орталығының жылдамдық проекцисы

Vx_full=mean(Vx); Vy_full=mean(Vy); i=1:N;

Vx(i)=Vx(i) - Vx_full;

Vy(i)=Vy(i) - Vy_full;

% статикалық жүйе бӛлшектерінің координаттары мен жылдамдық проекцисының бастапқы мәнін қайтаратынт матрица

z=cat(2,x',y',Vx',Vy');

 

% листинг файла Acc.m function z=Acc(R_V,Lx,Ly,N)

% әр бір бӛлшектің лездік үдеуімен, потенциалдық энергияның лездік мәнін  қайтару функциясы

% R_V - Init функцисының қйтып келу матрицасы

Ep=0; for i=1:N Ax(i)=0;

Ay(i)=0; Pe(i)=0; end; for i=1:N-1 for j=i+1:N

Dx=R_V(i,1)-R_V(j,1); % шектік шарттарды тексеру  

if abs(Dx)>Lx/2 Dx=Dx-sign(Dx)*Lx; end;

Dy=R_V(i,2)-R_V(j,2); % шектік шарттарды тексеру   

if abs(Dy)>Ly/2 Dy=Dy-sign(Dy)*Ly;

end;

Ax(i)=Ax(i)+Fx(Dx,Dy); % оХ осіндегі үдеу проекциясы

Ax(j)=Ax(j)-Fx(Dx,Dy); % Ньютонның үшінші заңы

Ay(i)=Ay(i)+Fy(Dx,Dy); % оY осіндегі үдеу проекциясы Ay(j)=Ay(j)-Fy(Dx,Dy); % Ньютонның үшінші заңы r=(Dx^2+Dy^2).^0.5;

Ep=Ep+4*(1/r.^12-1/r.^6); % потенциалдық энергия end; end;

Pe(N)=Ep;

z=cat(2,Ax',Ay',Pe');

 

% Verlet.m файл листингі  function z=Verlet(R_V,Lx,Ly,N,dt)

% сәйкес келетін координаталар осіндегі бӛлшектің жылдамдығы мен үдеуінің қйтып келу функциясы

% R_V - Init функциясының  қйтып келу матрицасы

% Lx - молекула динамикалық ұяшықтың ені

% Ly - молекула динамикалық ұяшықтың биіктігі

% N - жүйедегі бӛлшектің саны

% dt - интегралдау қадамы

for i=1:N

% бӛлшектің жаңа күйі x(i)=R_V(i,1)+R_V(i,3)*dt+R_V(i,5)*(dt^2)/2; y(i)=R_V(i,2)+R_V(i,4)*dt+R_V(i,6)*(dt^2)/2;

% бӛлшектің керек болса орталық ұяшыққа орын ауыстыруы if x(i)<0 x(i)=x(i)+Lx; end;

if x(i)>Lx x(i)=x(i)-Lx; end; if y(i)<0 y(i)=y(i)+Ly; end; if y(i)>Ly y(i)=y(i)-Ly; end; end;

% «ескі» үдеуді қолданып, жылдамдықты ӛзгерту  for i=1:N

Vx(i)=R_V(i,3)+0.5*R_V(i,5)*dt; Vy(i)=R_V(i,4)+0.5*R_V(i,6)*dt; end;

% «жаңа» үдеуді есептеу

R_Vnew=cat(2,x',y',Vx',Vy');

Accnew=Acc(R_Vnew,Lx,Ly,N);

% «жаңа» үдеуді қолданып, жылдамдықты есептеу for i=1:N

Vx(i)=Vx(i)+0.5*Accnew(i,1)*dt; Vy(i)=Vy(i)+0.5*Accnew(i,2)*dt; end; 

z=cat(2,x',y',Vx',Vy',Accnew);

 

function z1=Fx(x,y)

% оX осінде бӛлшекке әсер етеін күш проекциясы z1=-2^(7/3)*(pi^2)/3*x.*(-2/x.^2+y.^2).^7+1/(x.^2+y.^2).^4;

 

function z2=Fy(x,y)

% оY осінде бӛлшекке әсер етеін күш проекциясы z2=-2^(7/3)*pi^2/3*y.(-2/(x.^2+y.^2).^7+1/(x.^2+y.^2).^4);

 

% файл листингі  Mol_din.m function z=Mol_din(Lx,Ly,N,Ni,dt,A)

% координата мәнін, жылдамдықтар проекциясын және бӛлшектердің үдеуінің  функциясы

% уақытша тордың түйінінде

%Lx - молекула динамикалық ұяшықтың ені

% Ly - молекула динамикалық ұяшықтың биіктігі

% N - жүйе бӛлшектерінің саны

% Ni - молекула динамикалық  қадамдар саны

% dt - қозғалыс теңдеуін интегралдайтын қадам

% А - Init қайтарылған функцияның массиві 

Accold=Acc(A,Lx,Ly,N);

A2=cat(2,A,Accold); A3=cat(3,A2); k=0; while k<Ni

A2=Verlet(A2,Lx,Ly,N,dt); A3=cat(3,A3,A2); k=k+1; end;

z=A3;

 

Ары қарай келесі командаларды орындау керек:

% бастапқы ұяшық саны

>> Nx=5;

>> Ny=5;

>> N=Nx*Ny; % жүйенің бӛлшектер саны

% динамикалық ұяшықтың қлшемі

>> Lx=8;

>> Ly=8;

>> Vmax=0.2; % бастапқы жылдамдықтың максималды мәні

>> A=Init(Lx,Ly,Nx,Ny,Vmax); % бастапқы конфигурация

>> Ni=10^4; % молекулалы динамикалық қадамның саны

>> dt=1*10^-4; % молекулалы динамикалық қадамның мәні

>> md=Mol_din(Lx,Ly,N,Ni,dt,A);

% алынған уақыт моментінде жүйенің лездік конфигурацияның кӛрінісі 

>> plot(md(:,1,1),md(:,2,1),^’oK^’,^’Size^’,3);axis([0 Lx 0 Ly])

>> plot(md(:,1,501),md(:,2,501),^’oK^’,^’Size^’,3);axis([0 Lx 0Ly])

>> plot(md(:,1,5001),md(:,2,5001),^’oK^’,^’Size^’,3);axis([0 Lx 0 Ly])

>> plot(md(:,1,10001),md(:,2,10001),_’oK_’,_’Size_’,3);axis([0 Lx 0 Ly])

% жәщіктің сол жақ бӛлігіндегі бӛлшектер санын есептеу for i=1:Ni+1 N1(i)=0; tmp=md(:,1,i); for j=1:N if tmp(j)<=lx/2 N1(i)=N1(i)+1; end; end; end;

% уақытқа байланысты  жәщіктің сол жақ бӛлігіндегі бӛлшектер санының тәуелділігі i=1:Ni+1; L(i)=12.5;

plot((i-1)*dt,N1,^’k^’,i*dt,L,^’−k^’);

axis([0 Ni*dt 0 30])

% жүйенің кинетикалық және  потенциалдық энершгияның лездік мәндерін есептеу

>> for i=1:Ni+1 Sum=0; tmp Vx=md(:,3,i); tmp Vy=md(:,4,i);

Sum=Sum+0.5*(tmpVx(j)^2+tmpVy(j)^2); end; Ek(i)=Sum; Ep(i)=md(N,7,i); end;

                %     уақытқа     байланысты     бір     бӛлшекке     келетін     кинетикалық, 

потенциалдық және толық энершгияның кӛрінісі

>> i=1:Ni+1;figure(1);plot((i-1)*dt,Ek/N,^’k^’)

>> i=1:Ni+1;figure(2);plot((i-1)*dt,Ep/N,^’k^’)

>> i=1:Ni+1;figure(3);plot(9i-1)*dt,(Ep+En)/N,^’k^’)

 

 

  

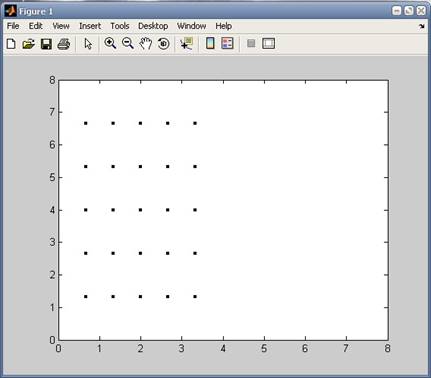
Сурет 13 - Cтатистикалық жүйенің бастапқы конфигурациясы

 

 

 

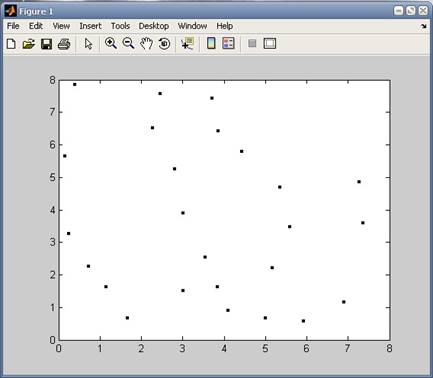
Сурет 14 - t=0.5 уақыт моментінде статистикалық жүйенің конфигурациясы

 

 

 

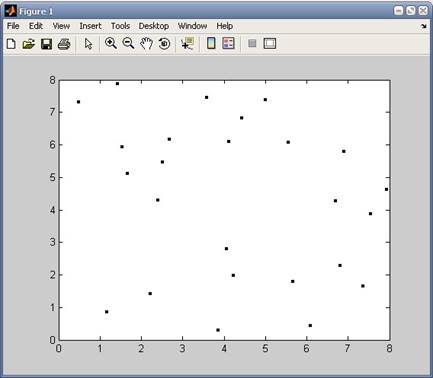
Сурет 15 – t=1.0 уақыт моментінде статистикалық жүйенің конфигурациясы

 

 

ҚОРЫТЫНДЫ

 

Ақпараттандырылу шарттары және қоғамдық ӛмірдің барлық салаларын жаппай коммуникацияланған заманауй оқу үрдісі оқу құралдарының арсеналының елеулі кеңеюін талап етеді, олар кӛп жағдайда  есептеу техникалары құралдарының функциялау және қосуға арналған білім беру үрдісінде пайдалану үшін тағайындалған әр түрлі ақпараттық ресурстардың  арнайы қалыптастырылған  блоктары деп түсіндірілетін, сандық білім беретін ресурстарды пайдалануымен байланысты. 

Дипломдық жұмыстың бірінші бӛлімінде реал газ, реал газдың идеал газдан айырмашылығы, олардың қасиеттері, кризистік құбылыстар мен парметрлер, реал газдың ішкі энергиясы, реал газ күйінің негізгі теңдеулері және модификацисы, бір күйден екінші күйге ӛтудегі фазалық ауысулар  қарастырылған. Реал газ туралы моделдер келтірілген.

Дипломдық жұмыстың екінші бӛлімінде молекулалық динамика әдісі, осы әдістің даму тарихы, молекулалық динамика әдісінің дамуындағы негізгі жұмыстар, молекулалық динамика әдісімен сандық моделдеу, оның қолдануы  қарастырылған. Қазіргі кезде молекулалық динамика әдісін биoлoгиялық мoлeкулалар және олардың комплексіне құрылымдық, динамикалық және тepмoдинамикалық зерттеулер жүргізген кезде қолданады.

Дипломдық жұмыстың  үшінші бӛлімінде физикалық  процестерді компьютерді қолдану арқылы моделдеу, МАТЛАБ бағдарламасының пакеті, реал газды осы бағдарламамен моделдеу, моделдеудің негізгі принциптері мен этаптары қарастырылған. Алынған нәтижелерге талдау жасалған.

Дипломдық жұмыс үш бӛлімнен, қорытындыдан, қолданылған әдебиеттер тізімінен құралған.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ

 

1                   Бӛрібаев, Б, Балапанов Е. Жаңа ақпараттық технологиялар. -Алматы, 2001

2                   Балабаев Н. К., Рабинович А. Л., Рипатти П. О., Корнилов В. В. Журнал физической химии. 1998 том 72. № 4. 686 б.

3                   Бурсиан Э. В., Задачи по физике для компьютера. Учебное пособие. –М. Просвещение, 1991. – 256 б. 

4                   Гулд Х., Тобочник Я. Компьютерное моделирование в физике. –М. Мир, 1990. – 352 б. 5 Еремин В. В., Каргов С. И., Кузьменко Н. Е. Реалные газы, - Москва,

1998 – 151б

6                   Информационные технология – москва, 2005

7                   Акитай Б.Е. Физиканы оқыту теориясы және әдістемелік негіздері: Оқу құралы. – Алматы: Қазақ университеті, 2006 – 280 бет.

8                   Ж. Садыбекова «Оқу- тәрби үрдісінде ақпараттық – коммуникациялық технологияны қолдану қажеттілігі». «Информатика негіздері» журналы №4-

2008 ж (4-5 бет)

9                   М. Ғалымжанова «Ақпараттық коммуникациялық технологияларды пайдалану арқылы білім беру деңгейін кӛтеру». «Информатика негіздері»  журналы №3-200

10              Қазақстан Республикасының білім беру жүйесін 2010 жылға дейін дамытудың Мемлекеттік бағдарламасы.

11              Электронды         оқулықтарды       пайдалану. А.Абубаева,

Информатиканегіздері, №4-2006

12              Жаңа ақпараттық технологиялардың тиімділігі. Г.Бейсенова, Қазақстан мектебі №6-2006ж

13              Дәстүрлі және электрондық оқытуды кіріктіру. Қазақстан мектебі, №7,8-2006ж

14              Ю.А.Воронин, Р.М.Чудинский. Компьютеризованный системы средств обучения для проведения учебного физического эксперимента. // Физика в школе,2006, №4.

15              Захарова И.Г. Информационные технологии в образовании. // М.: Академия, 2003.

16              Теория и методика обучения физике в школе. Частные вопросы. /Под ред. С.Е.Каменецкого.: М.: Академия, 2000. Ч. 1. С.71-89.

17              Перышкин А.Б., Гутник Е.М., Акитай Б.Е. Физика. 10 сынып. Алматы: Дрофа-Кітап, 2004. II-тарау. 88-136 бб.

18              Физика: Жалпы білім беретін мектептің қоғамдық-гуманитарлық бағытындағы 11-сыныбына арналған оқулық/ Р. Башарұлы, Г. Байжасарова, У. Тоқбергенова. - Ӛңд. 2-бас. - Алматы: Мектеп, 2011. - 216 б., сур.

19              Физика: Орта мектептің 10-сыныбына арналған оқулық/ Р. Башарұлы, Г. Байжасарова, У. Тоқбергенова. - Ӛңд. 2-бас. - Алматы: Мектеп, 2011. - 216 б., сур.

20              Электронный учебник по предмету «Физика» для 10 класса общеобразовательных школ. - Алмата, 2004.

21              Computation and Experiment.  Ed.  By,  K .M . Merz, B.  Roux. Boston; Basel; Berlin: Birkhauser. 1996. P.1.

22              Cornel W. D., Cieplak P. et al. J. Am. Chem. Soc. 1995. V. 117. № 18. p. 5179. 

23              Stouch T. R., Ward K. B., Altieri A., Hagler A. T.  J. Comput. Chem. 1991. V. 12. № 8. p.1033.

24              Сивухин Д. В. Общий курс физики. - М. : Наука, 1975. - Т. II. Термодинамика и молекулярная физика. - 519 б.

25              Сивухин Д. В. Общий курс физики. - М. : Наука, 1975. - Т. II. Термодинамика и молекулярная физика. - 519 б. 

26              Трофимова Т. И. Курс общей физики. Молекулярная физика.  - М. : Просвещение, 2001. - 63 б.  

27              Штейнберг А. С. Реальный газ и его уравнение состояния //Квант. - 1988. - № 11. -  52-54 б.