
Министерство образования и науки Самарской области
государственное бюджетное профессиональное образовательное учреждение
Самарской области
«Борский государственный техникум»
ДОКЛАД
По дисциплине: «Математика»
На тему: «Совершенствование форм и методов работы учителя математики»
Подготовила:
Ромаева Н. С. – преподаватель математики
с. Борское, 2020г.
Совершенствование форм и методов работы преподавателя математики
Будущее образования определяется не президентом отдельно взятой страны, не министром образования и даже не преподавателем. Каждый участник образовательного процесса сам решает, идти в ногу с будущим или вышагивать пятками вперед.
А.А.Гин
Новые требования, которые предъявляются к результатам освоения программы обучающимися, предполагают изменение содержания образования, опираясь на принципы метапредметности.
Под метапредметностью понимаются умения и универсальные учебные действия, как указано в новом образовательном стандарте. Выделяют следующие группы метапредметных умений:
1) умение планировать собственную деятельность;
2) способность эффективно действовать в группе;
3) компьютерная грамотность;
4) умение работать с источниками информации.
Опираясь на работы известных современных учёных А.В Хуторского, Н.В.Громыко, Ю.В.Громыко, О.В.Лебедева и А.Г.Асмолова, рассмотрим понятие метапредметных компетенций.
Метапредметный подход предполагает такое изменение организации образования, при котором знания воспринимаются, как то, что необходимо осмыслить и применить в жизни. При таком подходе возможно сформировать у обучающегося представление о дисциплине, как о системе знаний о мире, выраженном в числах и обеспечить преемственность всех ступеней образования.
Математика – это наука о фундаментальных структурах реального мира. На протяжении веков, развитие математики способствовало развитию научно-технического прогресса всего человечества. Математически образованная личность легко применит её технологии в изучении любой новой для человека проблематики.
Педагогика обязывает нас принимать обучающегося таким, каков он есть, но каждый студент – личность. И в группе всегда есть такие студенты, которые схватывают все на лету, и такие, которым все надо подробнейшим образом несколько раз пояснять; увлеченные математикой и не любящие ее. Насильно против воли человека научить невозможно. Когда-то Галилео Галилей сказал: «Вы не в состоянии научить человека чему-либо. Вы можете лишь помочь ему обнаружить это внутри себя». Дети учатся сами, а учителя, педагоги учиться только помогают. Нужно сделать так, чтобы ученик сам захотел, тогда он выучит. Стимулом к обучению служат эмоции, лучше, если положительные.
Инновационные технологии предполагают:
· повышение уровня мотивации к учебному труду;
· формирование высокого уровня развития обучающихся на основе включения их в постоянную усложняющуюся деятельность при активной поддержке преподавателя;
· постоянное повторение, систематизация знаний проговаривание вместе с преподавателем;
· ведущая роль – формирование доброжелательной атмосферы, создание позитивного отношения к преподавателю посредством индивидуального отношения к каждому студенту.
Педагогические технологии, используемые при этом:
· Личностно-ориентированная технология обучения
· Технология уровневой дифференциации.
· Проблемное обучение.
· Тестовые технологии
· Групповая технология
· Технология модульного обучения
· Информационно-коммуникационные технологии
· Здоровьесберегающие технологии
Цель: создание условий для развития у обучающихся качеств личности, необходимых для полноценной жизни в современном обществе:
ü инициативность
ü предприимчивость
ü коммуникабельность
Задачи:
· развитие способности и умений самостоятельной познавательной деятельности;
· овладение системой математических знаний и умений, необходимых для применения в практической деятельности;
· подготовка к самостоятельному решению проблем в различных сферах деятельности;
· формирование опыта разнообразной деятельности (индивидуальной, коллективной).
Успех обучения в значительной степени зависит от познавательной активности студентов, от того, насколько они заинтересованы. Новизна, практическая значимость содержания учебного материала, использование исторического материала, современных достижений науки способствуют привлечению внимания учащихся к обучению. А по организации учебного процесса:
1. применение нетрадиционных форм урока (уроки-соревнования, театрализованные уроки, уроки-игры, интегрированные, уроки-лекции, урок-практикум и т.д.);
2. использование разных форм учебной работы (групповые, индивидуальные, фронтальные, парные);
3. мотивация и стимулирование учащихся;
4. использование современных технологий, метапредметных связей, проектных и поисковых методов, технологии проблемного обучения.
Такие формы, методы и приемы я применяю на своих уроках и считаю, что они способствуют формированию устойчивых познавательных интересов у обучающихся.
Примеры активизации познавательной активности.
Нестандартные ситуации – как средство мотивации учащихся

Изучение
новой темы
Проблемные ситуации
• Представьте себе, что вы стоите перед дилеммой, либо получить 100 тыс. долларов прямо сейчас, либо в течении 28 дней получать монетку в 1 цент, который ежедневно удваивается. Чтобы вы предпочли?
Поисковая беседа
• «На обоих берегах реки растет по пальме, одна против другой. Высота одной 30 локтей, другой – 20 локтей. Расстояние между их основаниями – 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли ее одновременно. На каком расстоянии от более высокой пальмы появилась рыба?»
 Совместный
поиск выхода из проблемной ситуации
Совместный
поиск выхода из проблемной ситуации
• Что можно сказать о положении луча b? (Он проходит между сторонами развернутого угла (a1 a2))
• Почему можно сделать такое заключение? (он исходит из вершины развернутого угла и отличен от его сторон)
• Как можно представить градусную меру угла (a1 a2)? (По аксиоме измерения углов: (a1 a2) = (a1 b) + (a2 b) )
• Чему равна градусная мера развернутого угла? (180º)
Использование материала, выходящего за рамки школьной программы
· приемы быстрого счета;
· нетрадиционные методы решения задач (решение задачи с конца, метод графов и др.);
· методы и приемы решения геометрических задач.
Формула Пика
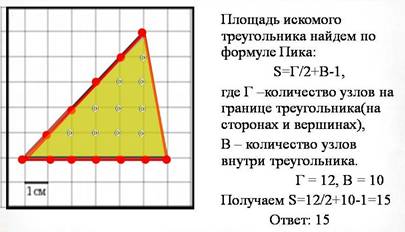
Умение применять знания для решения конкретных практических задач:

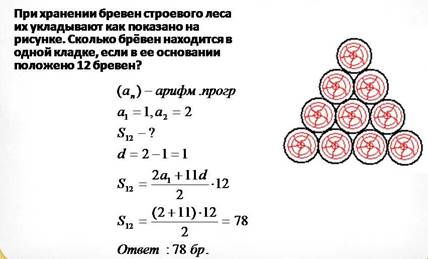
Абстрактная задача может быть практической:
Абстрактная задача : Решить уравнение x2-58x+480=0
Практическая: Имеется материал для построения забора длиной116 м. Можно ли загородить этим забором прямоугольный загон для уток на птицефабрике площадью 4,8 а. Определить стороны этого загона.
Такой подход к решению задач показывает учащимся реальную необходимость применения получаемых знаний для достижения стоящих перед ними практических целей.
Исторические задачи

Метод проектов на уроках
Типы заданий, предлагаемых ученикам в ходе проекта:
· практические задания (измерения, черчения с помощью чертежных инструментов, разрезания, сгибания, рисования и др.)
· практические задачи – задачи прикладного характера;
· проблемные вопросы, ориентированные на формирование умений выдвигать гипотезы, объяснять факты, обосновывать выводы;
· теоретические задания на поиск и конспектирование информации, ее анализ, обобщение и т.п.;
· задачи - совокупность заданий на использование общих для них теоретических сведений.
Урок
– проект по теме
Теорема Пифагора
За неделю до проведения урока класс был разделен на группы, каждая из которых получила задание.
Задание 1 группе: изучить биографию Пифагора, результаты представить в виде презентации и буклета;
Задание 2 группе: подготовить обзор доказательств теоремы Пифагора в виде презентации и публикации;
Задание 3 группе: изучить отражение теоремы Пифагора в литературе: в легендах, стихах, песнях, анекдотах, результаты представить в виде презентации;
Задание 4 группе: собрать исторические задачи, в решении которых применяется теорема Пифагора, результат оформить в виде публикации;
Задание 5 группе: изучить философские высказывания Пифагора, их связь с современностью, результат оформить в виде презентации.
Результаты этой работы были представлены на уроке.
Постоянная, органическая связь теории с практикой в преподавании математики обеспечивает такое усвоение обучающимися программного материала, при котором теория становится для них руководством к действию, к решению практических задач, возбуждает интерес к изучению математики, повышает творческую активность.
Список литературы
1. Данилов. И.К. Об игровых моментах на уроках математики // Математика в школе. – 2005.- №1.-
2. Демченкова Н., Моисеева Е. Формирование познавательного интереса у учащихся // Математика. -2004.- №19.
3. Минаева С. Формирование вычислительных умении в основной школе // Математика в школе.- 2006.- №2
4. Федотова Л. Повышение вычислительной культуры учащихся // Математика в школе. - 2004. - №43
5. Щукина. Г.И. Активизация познавательной деятельности учащихся в учебном процессе: Учебное пособие для студентов педагогических институтов. – М.: Просвещение, 1980.
Успех обучения в значительной степени зависит от познавательной активности студентов, от того, насколько они заинтересованы. Новизна, практическая значимость содержания учебного материала, использование исторического материала, современных достижений науки способствуют привлечению внимания учащихся к обучению. А по организации учебного процесса:
1. применение нетрадиционных форм урока (уроки-соревнования, театрализованные уроки, уроки-игры, интегрированные, уроки-лекции, урок-практикум и т.д.);
2. использование разных форм учебной работы (групповые, индивидуальные, фронтальные, парные);
3. мотивация и стимулирование учащихся;
4. использование современных технологий, метапредметных связей, проектных и поисковых методов, технологии проблемного обучения.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.