Эффективное обучение в рамках личностно ориентированного подхода на уроках математики

Эффективное обучение в рамках личностно ориентированного подхода на уроках математики

Под термином “личностно-ориентированный подход в обучении” понимается такой подход, при котором учитель в процессе обучения может контролировать качество полученных знаний каждого обучающегося и в зависимости от индивидуальных особенностей обучающегося совершенствовать их.

        Но как на практике осуществить индивидуальный личностный подход к каждому обучающемуся? Как, обучая  в одном классе, всех вместе, учитывать интересы каждого? Как изловчиться развивать личность каждого  в соответствии с его природными способностями?

        Простого однозначного ответа на эти вопросы нет и быть не может. Все зависит от личности учителя, обучающегося, от среды, в которой проходит обучение.

     Не уроках математики я стараюсь пробудить у обучающихся интерес к этой науке и его поддерживать.  Для этого,  необходимо тщательно продумывать, как доступно, понятно объяснять  новый материал, как заинтересовать обучающихся, как сделать так, чтобы они не просто слушали объяснение - лекцию, а стали соучастниками открытия, доказательства, важного вывода, чтобы уже во время объяснения новой темы они почувствовали себя творцами.

                                   "Плохой учитель преподносит истину, хороший учит ее находить" - эти слова немецкого педагога и математика 19 века Адольфа Дистервега надо не забывать, когда готовимся к урокам.

           Для успешного решения поставленных задач необходимо владение современными  образовательными технологиями и методиками и   эффективное применение их в практической профессиональной деятельности. Выбор и использование мною современных образовательных технологий определяется целями и задачами каждого конкретного урока, возрастными и индивидуальными особенностями обучающихся.

              Считаю, что основой эффективной практической деятельности учителя являются современные образовательные технологии. В своей педагогической деятельности использую следующие технологии:

· личностно-ориентированную;

· разноуровневого обучения;

· проблемного обучения;

· тестовые технологии;

· современные компьютерные технологии;( очень редко)

· развивающие творческие способности в процессе обучения  математике;

        Применяю различные формы организации учебного процесса: индивидуальную, групповую, коллективную. Индивидуальную форму работы провожу чаще при контроле усвоения нового материала по карточкам. В работе опираюсь на принцип индивидуализации обучения, что является основой личностно-ориентированной технологии и разноуровневого обучения. Знаю и учитываю различия в уровне развития способностей и возможностей своих учащихся, их познавательных интересов.

 С учащимися, имеющими повышенный интерес к предмету, организую индивидуальные консультации, помогаю им организовать самостоятельную образовательную деятельность в форме индивидуальных заданий и заданий для самоподготовки. Привлекаю таких учащихся для участия в интернет олимпиадах, конкурсах, проектах.

       Наиболее эффективной формой организации учебной деятельности учащихся при решении задач считаю групповую работу. Она обеспечивает индивидуальное развитие каждого учащегося, формирование межличностного интеллекта, а это в первую очередь означает высокое развитие коммуникативных компетенций. Мозговой штурм - самая интересная форма групповой деятельности. Во время этой работы мои ученики могут кратко и четко выражать свои мысли, учатся слышать и слушать друг друга. Таким образом, используя различные методы решения учебной проблемы, я решаю в работе с учащимися следующие задачи: обеспечить освоение учениками логической цепочки выдвижения предположений, аргументации своих предположений, доказательств выбора решений, выводов, опорных схем и конспектов, разработку проектов, что формирует теоретическое мышление и технологическую культуру учащихся, создаёт условия для индивидуального самовыражения, признания, самоутверждения каждого ученика как личности, формирует учебно - познавательные компетенции.

Наше время востребует нового человека – исследователя проблем, а не простого исполнителя. Сегодня обществу нужен человек-творец, умеющий самостоятельно и критически мыслить, способный видеть и творчески решать возникающие проблемы. Моя цель как педагога, как учителя математики,- средствами своего предмета научить учащихся думать, самостоятельно принимать решение, делать открытия, самостоятельно добывать знания, (при возможности) решать возникающие проблемы, нести ответственность за принятое решение - полностью согласуется с целями, которые решает школа и система образования в целом.

    Когда приходишь на урок, хочется, чтобы ученики стремились узнавать новое, хотели чему-то учиться, рассуждали и спорили, искали и доказывали. Приняв как аксиому тезис     «человека нельзя научить, развить, воспитать; он может только научить себя сам, то есть научиться, развиться, воспитаться», я понимаю, что мне нужно создать условия, при которых у учащихся появляется потребность  « включения» в активный процесс познания. Мне удается этого достичь путем использования технологии проблемного обучения. Соблюдение принципов организации проблемного обучения позволило мне достичь неплохих результатов. Эти результаты выражаются не столько в объеме полученных знаний, сколько в приобретении школьниками качеств, навыков, умений, способов мышления, познания, которые позволят им быть успешными и далее в учебной деятельности, формируют потребность в познании, в общении.

Конечно среди моих учащихся есть те, кто испытывает отрицательное отношение к математике, и моя главная задача исправить это. На уроках, построенных по технологии проблемного обучения, даже ученики, имеющие низкие учебные возможности, иногда добиваются успеха. Усвоение материала происходит в основном на уроке. В этом и вся проблема, что у учащихся нет возможности продолжить занятие вне школы.

       Особое место в моей методической копилке занимают тестовые технологии, которые вырабатывают у учащихся навыки ускоренного обдумывания выбора ответа, используя методы сравнения, исключения, взаимосвязей, по аналогии и т. д.     Тестирование способствует подготовке к сдаче ГИА.

        В своей практике использую метод рефлексии, который помогает научить обучающихся самооценки знаний. В начале года провожу входные контрольные работы, зачетные работы после изучения основных тем (глав), а  в конце—итоговые контрольные работы. Анализируя результаты контрольных работ, можно проследить общую картину  об изменениях в знаниях, и отследить  динамику роста качества  ЗУН. Данная система работы позволяет мне своевременно корректировать учебный процесс.

Этап актуализации субъектного опыта

Данный этап обычно сопровождается устной работой. Для этого использую, такие задания. Пример:

Тема: Числовая последовательность. (алгебра 9 класс)

 Устная работа. 1.Назовите пропущенный член последовательности:

а) 1; 3; 5; *; 9; … б) –10; 10; –10; 10; *; … в) а₁; …; а_{п – 2}; *; а_п; …

2.Последовательность задана формулой п-го члена, найти ее член с заданным индексом:

г) х_п = 5п – 2, х₅ = *  д) у_п = п³ – п, у₃ = * е) b_n = (–1)ⁿ · n, b₆ = *.

Последовательность задана несколькими первыми членами, задайте формулу п-го члена:

ж) 4; 8; 12; 16; … х_п = *  з) 7; 7; 7; …а_п = *            к) 3; 7; 11; 15; … х_п = *.

Актуализация знаний. 1. Назовите первые три члена последовательности:

а) a_n = n/2;                     б) b_n = 3n – 1;                      в) с_п = п² + 1.

2.Для последовательности, заданной первым членом и рекуррентной формулой, найдите второй и третий члены: г) x₁ = 2, x_{п + 1} =( х_n+2)/4; д) у₁ = 3, у_{п + 1} = у_п² – 5.

 Актуализация знаний и создание проблемной ситуации.

 Пример: (10 класс алгебра и начала мат. Анализа). «Лови ошибку!»На проверочном листе записаны свойства логарифмов с ошибками . Ваша задача рядом с ошибочным вариантом свойств записать их в правильном варианте.

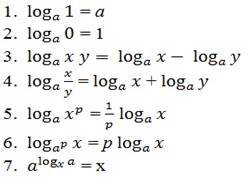
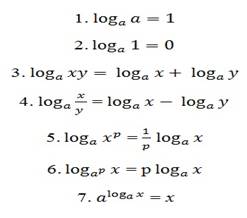
При изучении нового материала стараюсь “заразить” обучающихся поиском решения той или иной проблемы. Очень важно никого не обойти вниманием, опираясь на более подготовленных к логическим рассуждениям сильных обучающихся, не забывать о слабых, задавать им вопросы, подталкивать к верным выводам. Если он соучаствовал в рассмотрении новой темы, он будет по другому, по-доброму к ней относиться

Опыт работы показывает, что глубокие, прочные и, главное, осознанные знания могут получить все, если развивать у них не столько память, сколько логическое мышление.

Важным и значимым становятся математические сведения, если они затрагивают личность, если с ними связаны жизненный и личный опыт. При этом учебная ситуация преобразуется в личностно-значимую, а учебная информация – в событие самого обучающегося.

Для успешного выполнения упражнений, необходимо ответить на некоторые вопросы. На столах лежат карточки “Составьте соответствия” (11 класс алгебра и начала мат. Анализа)

Составьте соответствия

Закрепление изученного материала практически всегда сопровождаю заданиями на составление обратной задачи. Такая форма работы применима к любой теме курса математики. Если учащиеся способны составлять обратную задачу, значит, они понимают смысл данного задания.

Предлагаю выполнять самостоятельную работу по одному из предложенных вариантов: а) полностью самостоятельно; б) по аналогии с решениями упражнений, записанных на доске; в) с использованием учебника.

Создание ситуации успеха

Обучение и воспитание будут способствовать развитию обучающегося в том случае, если у него возникает интерес к учению. Но как повлиять на его формирование? Для того чтобы сформировать интерес у учащихся необходимо создавать ситуации успеха!

Без ощущения успеха  пропадает интерес к школе и учебным занятиям, поэтому педагогически оправдано создание для обучающегося ситуации успеха. Это можно создать различными речевыми оборотами, подбадривающими словами.

Хочу привести речевые обороты, которыми пользуюсь в своей практике для создания ситуации успеха

Этап проверки знаний

При проверке знаний учащихся, кроме перечисленных выше методов (тесты, карточки на выбор), выясняю степень усвоения материала учащимися с помощью листов взаимоконтроля, которые содержат перечень программных вопросов по изучаемой теме.

На данном этапе использую различные тестовые задания. (геометрия 9 класс)

 Работа по индивидуальным карточкам

I уровень (карточка №1)

1.      В треугольнике ΔMNK МКN = 150º, МN = 8, а площадь треугольника равна 20. Найдите NK.

2.      В параллелограмме один из углов равен 45º, а его стороны равны 5 см и 8 см. Найдите его площадь.

3.      В прямоугольнике диагональ равна 12 см, а угол между диагоналями 30º. Найдите площадь прямоугольника.

II уровень (карточка№2)

1.      Найдите площадь параллелограмма, если его диагонали равны 8 см и 12 см, а угол между ними равен 45º.

2.      В треугольнике МКN N= 150º, МN = 4 см, NК = 6 см, NЕ – биссектриса треугольника . Найдите площадь треугольников МNЕ и NКЕ.

3.      Медианы ΔABC пересекаются в точке О, АВС = 30º, АВ =4 см, ВС = 6 см. Найдите произведение площадей треугольников АОС, ВОС, ВОА.

Тест на определение истинности (ложности) утверждения и правильности формулировок определений

1.      В треугольнике против угла в 150° лежит большая сторона. (И)

2.      В равностороннем треугольнике внутренние углы равны между собой и каждый равен 60°.(И)

3.      Существует треугольник со сторонами: 2 см, 7 см, 3 см. (Л)

4.      Прямоугольный равнобедренный треугольник имеет равные катеты. (И)

5.      Если один из углов при основании равнобедренного треугольника равен 50°, то угол, лежащий против основания, равен 90°.(Л)

6.      Если острый угол прямоугольного треугольника равен 60°, то прилежащий к нему катет равен половине гипотенузы. (И)

7.      В равностороннем треугольнике все высоты равны. (И)

8.      Сумма длин двух сторон любого треугольника меньше третьей стороны. (Л)

9.      Существует треугольник с двумя тупыми углами. (Л)

10.  В прямоугольном треугольнике сумма острых углов равна 90°.(И)

11.  Если сумма двух углов меньше 90°, то треугольник тупоугольный. (И)

Итоговым этапом урока является рефлексия. Высказывается каждый обучающийся, и уже с учётом сказанного планирую следующие уроки, ведущие к новым знаниям. В диалоге с ними не просто повторяются формулировки нового материала, а систематизируется весь изученный к этому моменту материал и ситуации его применения.