С.А. Агалаков

Уравнения и неравенства с параметром

Приведем общие замечания о решении задач с параметром.

Уравнение (неравенство) с параметром содержит, кроме основной неизвестной, дополнительную — параметр. Процесс решения задач с параметром более сложен, чем в обычном случае. Это связано с тем, что, во-первых, часто приходится разбирать несколько случаев (в зависимости от значения параметра), во-вторых, как правило, нельзя проверить все полученные значения параметра, подставляя их в исходное уравнение. Поэтому при решении уравнений и неравенств с параметром следует особое внимание уделять эквивалентности преобразований, накладывая, если необходимо, ограничения, отсекающие посторонние решения.

Задачи с параметром можно разделить на два вида.

К первому виду относятся задачи, в которых требуется найти все значения параметра, при которых выполняются условия, сформулированные в задаче. Второй вид — это задачи, в которых необходимо найти все значения неизвестной, при которых выполняются условия задания при заданных значениях параметра. Задачи второго типа, как правило, сводятся к задачам первого типа, если в качестве параметра взять неизвестную, а неизвестной считать параметр.

В общем случае, решение любых уравнений или неравенств с параметром происходит по обычной схеме: ОДЗ, решение, проверка. В процессе решения следует выполнять равносильные преобразования.

 Обычно решение задач с параметром сводится исследованию линейных и квадратных уравнений и неравенств.

Самые простые уравнения с параметром — линейные. Процесс решения таких уравнений не сложен: сначала приводим к виду Ax = B , затем рассматриваем два случая: A = 0 и A ¹ 0 .

Линейные неравенства с параметром вида Ax < B решают, рассматривая, три случая: A < 0, A = 0 и A > 0.

Пример 1. (Демо ЕГЭ2007). Найдите все значения x , которые удовлетворяют неравенству (2a -1)x² <(a +1)x + 3a при любом значении параметра a , принадлежащем промежутку (1;2 .)

Решение. Эта задача относится ко второму типу, поэтому, считая параметр a неизвестной, а неизвестную x — параметром, приведем

2

неравенство к виду: (2x² - x - 3)a + -( x² - x) < 0 . Это неравенство является линейным относительно неизвестной a . Рассмотрим три случая. В каждом случае будем использовать график линейной функции f( )a = - - +- -(2x² x 3)a ( x² x).

1.         Коэффициент при неизвестной 2x² - x - 3 < 0. В этом случае неравенство выполняется при всех a ^Î (1; ²), если прямая f( )a = - - +- -(2x² x 3)a ( x² x) пересекает ось абсцисс в точке, расположенной не далее 1. Значит, эта ситуация описывается следующей системой неравенств: ìïïïíïïïî2fx₍1²₎-£x0.- 3 < 0,

Решая эту систему, получаем:

ìïïíïïï⁽₍xx ++1 21⁾₎⁽₍xx-- <33₎⁾£ 00, Û - < £1      x          1,5 . î

2.         Коэффициент при неизвестной 2x² - x - 3 = 0 , т. е. x =-1 или

x = 1,5 .

Подставив x =-1 в неравенство, имеем: 0 < 0. Это неравенство не выполняется ни при каких значениях a . Значит, x =-1 — не удовлетворяет условию задачи.

Подставляя x = 1,5 в неравенство, получаем -2,25-1,5 < 0 . Это неравенство выполняется при всех значениях a . Значит, x = 1,5 — удовлетворяет условию задачи.

3.         Коэффициент при неизвестной 2x² - - >x 3 0. В этом случае неравенство выполняется при всех a Î(1;2), если прямая f( )a ⁼(2x² - -x ³)a ^{+ - -}( x^{2 x}) пересекает ось абсцисс в точке, рас-

положенной не ближе 1. Значит, эта ситуация описывается следующей

ìïï

системой неравенств: ïíïïïî2fx(22)- - >£x0. 3 0,

Решая эту систему, получаем:

ìïïíïï⁽₍xx ++ 1 21⁾₎⁽₍xx--23₎⁾£>00, Û 1,5 < x £ 2 . î

3

4.         Объединяя полученные в каждом из трех случаев ответы, имеем: - <1 x £1,5 , x = 1,5 , 1,5 <x £ 2 , т. е. x Î -( 1;2].

Ответ: (-1;2].

Решение квадратных уравнений и неравенств с параметром рекомендуется проводить в два этапа: предварительный анализ, затем решение задачи.

На первом этапе выясняются все возможные случаи выполнения условий задания. Для этого рассматриваются следующие ситуации:

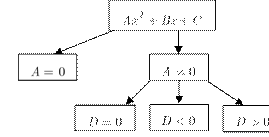
 В ходе анализа используются: связь между знаком дискриминанта D и числом корней, расположение параболы относительно оси абсцисс.

На втором этапе происходит разбор всех случаев выполнения условий задания. Здесь используются различные свойства квадратного трехчлена: связь между знаком дискриминанта и числом корней, расположение параболы относительно оси абсцисс, теорема Виета, формулы для вычисления координат вершины параболы.

Использование графиков

 Некоторые задачи с параметром удобно решать, используя графики функций.

Сначала рассмотрим задачи на наибольшее и наименьшее значения функции. Для решения этих задач построение графика не требуется. Достаточно знать только общий вид графика соответствующей функции.

Пример 2. При каких значениях параметра a наименьшее значение функции y = + + -x² 3x |x a | меньше -2 ?

Решение. Раскрывая знак модуля, нетрудно заметить, что график данной функции состоит из частей двух парабол, "склеенных" в точке с абсциссой x = a : y = x² + 4x -a при x ³a и y = x² + 2x + a при x a< .

Следовательно, наименьшее значение исследуемая функция принимает или

4

при x = a (точка "склеивания"), или при x =-2 (абсцисса вершины первой параболы), или при x = -1 (абсцисса вершины второй параболы).

Мы перечислили все возможные точки, которых функция может достигать своего наименьшего значения. Поэтому достаточно выяснить, когда в данных точках функция принимает значение меньше -2 , и объединить полученные значения параметра a .

Вычислим значения функции в указанных точках, сравним с заданным числом и найдем ограничения на параметр a :

x = Þ + <- Þ + + < Þ- < <-a    a²                                      3a        2          a²                                      3a        2          0          2          a          1; x = -2 Þ - 2 + -2 -a< -2 Þ-2 -a< 0 Þ               Æ ; x =-1Þ- +- - <- Þ - - < ÞÆ21 a21 a0           .

Объединяя найденные значения a , получаем

Ответ: -2 < a < -1 .

Задания

1.      Найдите количество целых значений параметра a , при которых

неравенство x - + +2a 2x   a £15 имеет хотя бы одно решение. 

2.      Найдите все значения параметра a , при которых неравенство x² + x+ |x -a | + 29 £ 0 не имеет решений. 

3.      Найдите все значения параметра a , при которых неравенство x²- |x -a | - |x -1| +3 ³ 0 выполняется при всех действительных значениях x . 

4.      Найдите все значения параметра a , при которых неравенство 2x² + ax + 7 > 1 не имеет решений на отрезке [1;3].

Теперь рассмотрим задачи, в ходе решения которых целесообразно использовать графики функций.

Пример 3. При каких значениях параметра a уравнение x x - 6x + a -1 = 0 имеет два различных корня?

Решение. Представим уравнение в виде: x x - 6x = 1 -a . С помощью функций y = x x - 6x и y = 1 -a исходная задача сводится к следующей: при каких значениях параметра a графики функций y = 1 -a и y = x x - 6x пересекаются ровно в двух точках? Решим поставленную задачу. Для этого построим график функции y = x x - 6x . Используя определение модуля числа, имеем: если x ³ 0 , то y = x² - 6x , если же x < 0 , то y = -x² - 6x . Следовательно, 5

нужно построить график первой функции и взять ту часть, которая расположена над интервалом x ³ 0 . У графика второй функции следует оставить часть, расположенную над интервалом x < 0 . Искомый график — это объединение этих двух частей.

График функции y = x² - 6x — парабола с "ветвями", направленными вверх, пересекающая ось абсцисс в точках 0 и 6 и имеющая вершину с координатами x₀ = 3 , y₀ = y(3) = -9 . График функции y = -x² - 6x имеет следующие характеристики: "ветви" направлены вниз, пересекает ось абсцисс в точках 0 и 6, x₀ = -3, y₀ = y(-3) = 9

— координаты ее вершины. 

В результате построения этих двух графиков и оставления необходимых частей, получаем следующий рисунок:

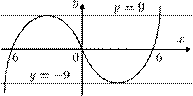
Рис. 1

 Графиком функции y = 1 -a является прямая, параллельная оси ОХ. С помощью рис. 1 находим, что имеются всего две горизонтальные прямые, пересекающие график функции y = x x - 6x в двух точках: y = -9 и y = 9 . Следовательно, либо 1 -a = -9 , либо 1 -a = 9 .

Решая эти уравнения, получаем Ответ: a = 10 , a = -8.

Задания

5.    Найдите все значения параметра a , при которых уравнение x x + 2a + 1 -a = 0 имеет только один корень.

6.    Найдите все значения параметра a , при которых неравенство 2 |x -a |< 2ax - 2 - x² имеет решение.

6

Задания ЕГЭ 2013 года

Рассмотрим пример выполнения задания С5 из демонстрационного варианта 2013 года.

Пример 6. Найдите все значения a , при каждом из которых наименьшее значение функции f( )x = 2ax+ |x² - 8x + 7 | больше 1.

Решение. Пусть 1. Функция f имеет вид:

a) при x² - 8x + 7 ³ 0 : f( )x = x² + 2(a - 4)x + 7 , а её график есть две части параболы с ветвями, направленными вверх, и осью симметрии x = -4 a ;

б) при x² - 8x + 7 < 0 : f( )x = - x² + (2a + 8)x - 7 , а её график

есть часть параболы с ветвями, направленными вниз.

Все возможные виды графика функции f (x) показаны на рисунках:

2.          Наименьшее значение функция f( )x может принять только в точках x = 1 или x = 7 , а если 4 -a Ï éêë1; 7ûùú – то в точке x = 4 -a .

3.          Наименьшее значение функции f больше 1 тогда и только тогда, когда

ìï_ï^ïïíff(1)(7)>>11,, Û ï^ïïíïïïïïï_ïïìï1422 (4aaa>>-1,1a,) + a₂ - 9 > 1 Û ï ïïïîf(4 -a) > 1 î

7

Û ïïïïïìïïîïa > 211, , Û êêêêéêêêêïïïíïïîïìïìïïíïïïaa321a2³<2--3a8,a8<a+3-,108 << 00 Û ïïíïïa >2 -148a + 1 - a2 - 9 < 0

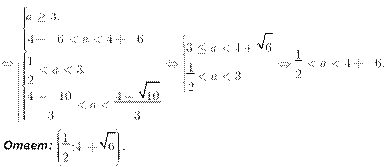
ïïï2aêïïî ïêë

Ниже приведены задания из вариантов ЕГЭ 2010-2012 годов.

Задания

7.         Найдите все значения a , при каждом из которых наименьшее значение функции f x( ) = 4ax + x² - 8x + 7 меньше 1.

8.         Найдите все значения a , при каждом из которых функция f( )x = x² - 2 x -a² -10x имеет хотя бы одну точку максимума.

9.         Найдите все значения a , при каждом из которых наибольшее значение функции f( )x = x² - 8 x -a - 2x ^{на отрезке} ëé-4;7ùû не принимает-

ся ни на одном из концов этого отрезка.

10.       Найдите все значения a , при каждом из которых любая прямая, перпендикулярная оси ординат, имеет нечетное число общих точек с графиком функции f( )x = (2a - 3)x -(x + 3) x -a .

11.       Найдите все значения a , при каждом из которых уравнение x +2 1 = a x - 3 на промежутке ^éë0;+^¥) имеет более двух корней.

8

12.       Найдите все значения a , при каждом из которых уравнение x5 - 3 = ax - 2 на промежутке (0;+^¥) имеет более двух корней.

13.       Найдите все значения a , при каждом из которых уравнение

1 - 2x = a - 7 x имеет более двух корней.

Ответы к заданиям

1. -6 £ a £ 6 . 2. a> . 3. -2 £ £a 1 . 4. -£ £a -8 .

5. a< ¹₂( 5 -1), a> 1 . 6. a < - 2, a >          2 . 7. a< , a> .

8. - < <-6 a    2 , 2< <a    6 . 9. - < <2 a 3 . 10. a £ 0 .

11. ¹ <a£ 2 . 12. ⁶ < <a 5 . 13. ⁷ £ <a 25 .

        2           3         5           4         2            7