К НОВОЙ ОФИЦИАЛЬНОЙ

ДЕМОНСТРАЦИОННОЙ ВЕРСИИ ЕГЭ

СОЗДАНО РАЗРАБОТЧИКАМИ ЕГЭ

Под редакцией И. В. Ященко

МАТЕМАТИКА

ПРОФИЛЬНЫЙ УРОВЕНЬ

ТИПОВЫЕ ТЕСТОВЫЕ

ЗАДАНИЯ

2017

ГОСУДАРСТВЕННЫЙЕДИНЫЙ                                                                             ЭКЗАМЕН

ЕДИНЫЙ ГОСУДАРСТВЕННЫЙ ЭКЗАМЕН

Под редакцией И. В. Ященко

МАТЕМАТИКА

ПРОФИЛЬНЫЙ УТОВЕНЬ

типовьњ ТЕСТОВЫЕ ЗАДАНИЯ

10 вариантов заданий Ответы и решения

Критерии оценок

Бланки ответов

ИзДательство

«ЭКЗАМЕН»

МОСКВА

2017

удк 372.8:51

ББК 74.262.21

ЕЗЗ

ЕЗЗ ЕГЭ 2017. Математика. Профильный уровень. Типовые тестовые задания / И. В. Ященко, М. А. Волчкевич, И. Р. Высоцкий, Р. К. Гордин, П. В. Семёнов, О. Н. Косухин, Д. А. Фёдоровых, А. И. Суздальцев, А. Р. Рязановский, И. Н. Сергеев, В. А. Смирнов, А. В. Хачатурян, С. А. Шестаков, Д. Э. Шноль; под ред. И. В. Ященко. — М. : Издательство «Экзамен»,

2017.— 55, [1] с. (Серия «ЕГЭ. ОФЦ. Типовые тестовые задания») ISBN 978-5-377-11100-9

Типовые тестовые задания по математике содержат 10 вариантов комплектов заданий, составленных с учётом всех особенностей и требований Единого государственного экзамена по математике профильного уровня в 2017 году. Назначение пособия предоставить читателям информацию о структуре и содержании контрольных измерительных материалов 2017 г. по математике профильного уровня, степени трудности заданий.

В состав авторского коллектива входят специалисты, имеющие большой опыт работы в школе и вузе и принимающие участие в разработке тестовых заданий для ЕГЭ.

В сборнике даны ответы на все варианты тестов и приводятся решения всех заданий одного из вариантов. Кроме того, приведены образцы бланков, используемых на ЕГЭ для записи ответов и решений.

Пособие может быть использовано учителями для подготовки учащихся к экзамену по математике в форме ЕГЭ, а также старшеклассниками и выпускниками — для самоподготовки и самоконтроля.

Приказом № 699 Министерства образования и науки Российской Федерации учебные пособия издательства «Экзамен» допущены к использованию в общеобразовательных организациях.

удк 372.8:51

ББК 74.262.21

Подписано в печать 09.08.2016. Формат 60х90/8.

Гарнитура «Школьная». Бумага газетная. Уч.-изд. л. 2,63. Усл. печ. л. 7. Тираж 10 ООО экз. Заказ 2412/16.

ISBN 978-5-377-11100-9

 Ященко И. В., Волчкевич М. А., Высоцкий И. Р.,

Гордин Р. К., Семёнов П. В., Косухин О. Н.,

Фёдоровых Д. А., Суздальцев А. И., Рязановский А. Р.,

Сергеев И. Н., Смирнов В. А., Хачатурян А. В.,

Шестаков С. А., шноль Д. Э., 2017

 Издательство «ЭКЗАМЕН», 2017

СОДЕРЖАНИЕ

Инструкция по выполнению работы

Вариант 1

Часть 1

Часть 2

Вариант 10

Часть 1.42 Часть 244

Решение заданий

Вариант 10. Часть 2 50

Инструкция по выполнению работы

Экзаменационная работа состоит из двух частей, включающих в себя 19 заданий. Часть 1 содержит 8 заданий с кратким ответом. Часть 2 содержит 4 задания с кратким ответом и 7 заданий с развёрнутым ответом.

На выполнение экзаменационной работы по математике отводится З часа 55 минут (235 минут).

Ответы к заданиям 1—12 записываются в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов

При выполнении заданий 13—19 требуется записать полное решение и ответ в бланке ответов № 2.

Все бланки ЕГЭ заполняются яркими чёрными чернилами. Допускается использование гелевой, капиллярной или перьевой ручек.

При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы.

Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.

Желаем успеха!

Справочные материалы

sin а + cos ос = 1 sin2a = 2 sin а • cos а

cos 20 = cos ос — sin се sin (а + р) = sin а • соф + cosa • sin cos(a + р) = cosa • cos — sin а • sin

Результаты выполнения заданий с ответом в краткой форме

зоошоошоооошооо zooooooooooooooo;oooooooooooooooo боошоошоооошооо;ооооооооооооооо

600000000000000060000000000000000 600000000000000600000000000000 боошоошоооошооо;оооооошооооооооо

боооооооооооооо;оошоооооооооооо бооооооооооооооооо;оошоооооооооооо

вооооооооооооооо sooooooooooooooo бооооошоооооооо;оошоошоооооооо боошоошоооошооо;оошоошоооошооо

ш-оооооооооооооош ш-ооооооошоошоош ш-ошооооооооооош ш-оооооооооошаза:п о-оатоооооопооо о-оооооооооооооош

、E図Hヒー「OOY aPCTBeHHbll>I SKaaMeH

…ん… 2皿ⅢⅢ旧旧Ⅲ Ⅲ Ⅱ Ⅱ

P              H H npe¥Ta npeAMera

3HaqeHVIR YKaaaHHbl><日曰u」eロone ⅵ3 SfiAHKA PE「L/ICTPAUI/IL/I

OTBeqaq Ha 3aaaHhA TecTa, nVILUhTe aKKypaTHO h 0a3500 BO, C05れa pa3MeTKY CTpaH駲日. He 3a6YAbTe YIG3aTb HOMep 3aaaHhR, Ha KOT000e Bbl 0TBæaere. ソcnOB 3 at-MA ne enhCblBaTb He H米HO.

BH¼MAH¼Eー4を村村、一朝6町村リ0 0れ30eamb moれト0 003M・cm村0 0 ðg′M府′材M 6・村を03を村村0を0れを・m・

o       ロロロロロ0ロロロ00000ロ00000000000ロ00000ロ00

0000ロロロ00ロ00000ロ00000000000000000000

00ロロロロ0ロ00ロ00ロ0ロロロロ0ロ0000ロ00000ロ0ロ00

00ロ000000000000ロロ000000000ロロロロ0ロ0ロ00 00ロ0000000000ロ000ロ00ロ00000ロ0000ロ0000 ロロロロロロロロロロロロロロ0ロ00000000000000000000 ロロロ0ロロロロ0ロ0ロロロ0ロ0ロロ0000000ロ00ロ000ロ00 00ロ0ロ0ロ000ロロロ00ロロロロ0ロ00000ロ0ロロ000000 0ロロ000000ロロロロ00ロロロ0000000000000ロ0ロ00 ロロロロロ0ロ0ロ000ロ00ロロ0000000000000000000 ロロロロロ000ロ0ロロロロロロロロロロロ000000000000000 0ロロ0ロ0ロ000ロ0ロロ0ロロロ0ロロ00ロ0000ロ0000000 ロ0ロ0ロ0ロ0000ロ0ロ000000000ロ000000000000 000ロロ000000ロロ動ロ000ロロロロ00000000000000

o       ロ0ロ0000ロ0ロロロロロ000000000000000000000

00000000000ロロロロ000ロロロロ0ロ0ロ0000000000

000000000000ロ000000ロ0000000000000ロ00

o       ロ0ロ0000000ロロロロ0ロ00ロ0ロ00000000000ロ0ロ

00000000000ロ0ロロ0ロ0ロ0ロ0ロロ000000000ロ00

000ロ0000000ロ0ロロ000ロ0ロロロロロロ00ロ000000ロ

00000000000000000000ロ0ロロ0ロ00000ロ0ロ0ロ

00000000000ロ00000000ロ0ロ0ロ0000000000ロ

00000000000ロ00000000ロ0ロロロ00000ロ00000

0000000000000ロ0000000000000000ロ00ロ0ロ

000000ロ000000000000000ロロロ0ロ0ロ0ロロロロロロ

000000ロ0000000000000ロロロロロ000000ロロ0ロロ

000000000000000000000ロロ0ロロ000000ロロロロ

000000ロ0ロ0ロ00000000000ロ0ロ00000ロ0ロ0ロロ

000000000000000000000000ロロロ0ロ0ロロロロロロ

0000000ロ000000000000000000ロ00ロロロ00ロ0

0000000000ロ0000000000000000000000ロロロ

000000000000000000000ロ0000ロロ00000ロロ0 00000000ロ0000000000000ロ0000ロ0ロロロロロロ0

ftp駲HeAOCTaTKe MecTa OTBeTa hcnonト3YhTe 2000THY0 CTOPOHY 6naHKa

0

                                   ВАРИАНТ 1                                     

Часть 1

1.            Пакет молока стоит 21 рубль 30 копеек.

Какое наибольшее количество пакетов молока можно купить на 500 рублей?

2.            Первый посев семян петрушки рекомендуется проводить в апреле при дневной температуре воздуха не менее +6 ^о с. На рисунке показан прогноз дневной температуры воздуха на первые три недели апреля. Определите, в течение скольких дней за этот период .моэкно производить посев петрушки.

1 з 5 7 9 11 13 15 17 19 21

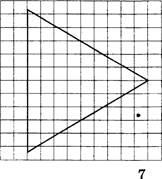
З. На клетчатой бумаге с размером клетки 1х1 изображён равносторонний треугольник. Найдите радиус вписанной в него окружности.

4.             Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвуют 56 шашистов, среди которых 12 участников из России, в том числе Валерий Стремянкин. Найдите вероятность того, что в первом туре Валерий Стремянкин будет играть с каким-либо шашистом из России.

5.             Найдите корень уравнения 5 ⁴ = 25.

6.             Отрезок АВ является хордой окружности с центром О. Найдите угол между прямой АВ и касательной к окружности, проходящей через точку А, если угол АОВ равен 56 ⁰ . Ответ дайте в градусах.

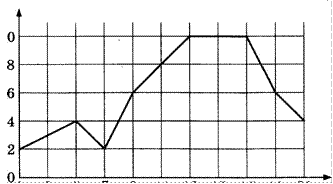
7.             На рисунке изображены график функции у = f (х) и касательная к этому графику, проведённая в точке хо е, Касательная задана уравнением у = —2х + 15 . Найдите значение производной функции у — ——f(x)+5 в точке хо.

у - -2х + 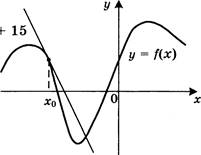15

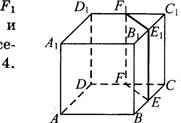
8.             В кубе АВСТ1В1СР1 точки Е, Р, Е1 и являются серединами рёбер ВС, DC, ВIС1 и DlC1 соответственно. Объём призмы, отсекаемой от куба плоскостью EFF1, равен 14. Найдите объём куба.

Часть 2

9.             Найдите значение выражения (558² — 23 ² ) : 581.

10.        Ёмкость высоковольтного конденсатора в телевизоре С = 4 • 10 -6 Ф. Параллельно с конденсатором подключён резистор с сопротивлением R = 2 • 10 ⁶ Ом. Во время работы телевизора напряжение на конденсаторе Uo = 22 кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением t = aRC log2 (с), где = 1,7 ом • Ф постоянная. Определите напряжение на конденсаторе, если после выключения телевизора прошло 27,2 секунды. Ответ дайте в кВ (киловольтах).

11.        В сосуд, содержащий 7 литров 15-процентного водного раствора некоторого вещества, добавили 8 литров воды. Сколько процентов составит концентрация получившегося раствора?

12.        Найдите наибольшее значение функции

у = (21 — х)е^{х 20}

на отрезке [19; 21].

13.        Решите уравнение

                                                (tg х +          lQg13(2 sin² х)

х) — 0. log31    cos

14.        В правильной четырёхугольной пирамиде SABCD с вершиной S сторона основания равна 4. Точка 1., — середина ребра SC. Тангенс 2Jii угла между прямыми BL и SA равен

17

а) Пусть О — центр основания пирамиды. Докажите, что прямые ВО и LO перпендикулярны.

б) Найдите площадь поверхности пирамиды.

2х ² -10х +6

15.        Решите неравенство

16.        Окружность с центром О вписана в угол, равный 60⁰ . Окружность большего радиуса с центром 01 также вписана в этот угол и проходит через точку О.

а) Докажите, что радиус второй окружности вдвое больше радиуса первой.

б) Найдите длину общей хорды этих окружностей, если известно, что радиус первой окружности равен 245

17.        В двух областях есть по 90 рабочих, каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,3 кг алюминия или 0,1 кг никеля. Во второй области для добычи х кг алюминия в день требуется х ² человеко-часов труда, а для добычи у кг никеля в день требуется у ² человеко-часов труда.

Для нужд промышленности можно использовать или алюминий, или никель, причём 1 кг алюминия можно заменить 1 кг никеля. Какую наибольшую массу металлов можно добыть в двух областях суммарно для нужд промышленности?

18.        Найдите все значения параметра а, при каждом из которых нерах ² + х —2а

венство—1 2 не имеет решений на интервале (1; 2).

19.        Решите в целых числах уравнение з^п + 8 = х .

ВАРИАНТ 2

Часть 1

1.            Для покраски потолка требуется 140 г краски на 1 м² . Краска продаётся в банках по З кг. Какое наименьшее количество банок краски нужно купить для покраски потолка площадью 42 м² ?

2.            Мощность отопителя в автомобиле регулируется дополнительным сопротивлением, которое можно менять, поворачивая рукоятку в салоне машины. При этом меняется сила тока в электрической цепи электродвигателя чем меньше сопротивление, тем больше сила тока и тем быстрее вращается мотор отопителя. На рисунке показана зависимость силы тока от величины сопротивления. На оси абсцисс откладывается сопротивление (в Омах), на оси ординат — сила тока в Амперах. Ток в цепи электродвигателя уменьшился с 8 до 4 Ампер. На сколько Омов при этом увеличилось сопротивление цепи?

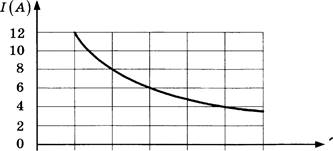
R(OM)

0,5 1,0 1,5 2,0 2,5 3,0

З. Найдите площадь трапеции ABCD, изображённой на клетчатой бумаге с размером клетки 1 х 1 (см. рис.).

4.             Конкурс исполнителей проводится в З дня. Всего заявлено 80 выступлений — по одному от каждой страны. В первый день запланировано 20 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?

5.              Решите уравнение log25(2 — 3х) = 0,5.

6.             В треугольнике АВС углы А и В равны соответственно 45 ⁰ и 67 ⁰ . Найдите угол между биссектрисой и высотой, проведёнными из вершины С. Ответ дайте в градусах.

7.             На рисунке изображён график функции у = f(x). Прямая, проходящая через точку (—1; 1), касается этого графика в точке с абсциссой З. Найдите Г(З).

8.             В сосуде, имеющем форму конуса, уровень жидкости достигает 1

    2 высоты. Объём жидкости равен 25 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

Часть 2

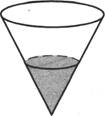
21

9.             Найдите cosa , если sina —           И ОС Е- 5          2

10.        Высоту над землей (в метрах) подброшенного вверх камня можно вычислять по формуле h(t) 1,4 + 14t — 5t ² , где t — время в секундах. Сколько секунд камень будет находиться на высоте более 8 метров?

11.        Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 60 км/ч, а вторую половину времени со скоростью  46 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

12.        Найдите точку минимума функции у = х^з — 12х ² + 15 .

13.        а) Решите уравнение 2sin(7t + х) • cos — + х = sinx .

б) Найдите все корни этого уравнения, принадлежащие отрезку [— 5л; — 4.л] .

14.        В правильной шестиугольной призме ABCDEFAIB1C1DIEIF1 стороны основания равны 5, а боковые рёбра равны 11.

а) Докажите, что прямые СА и CID1 перпендикулярны.

б) Найдите площадь сечения призмы плоскостью, проходящей через вершины С, „41 и F1 .

15.        Решите неравенство log5 х

16.        Две окружности касаются внутренним образом. Третья окружность касается первых двух и их линии центров.

а) Докажите, что периметр треугольника с вершинами в центрах трёх окружностей равен диаметру наибольшей из этих окружностей.

б) Найдите радиус третьей окружности, если известно, что радиусы первых двух равны З и 2.

17.        31 декабря 2014 года Олег взял в банке некоторую сумму в кредит под некоторый процент годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на а%), затем Олег переводит очередной транш. Если он будет платить каждый год по 328 050 рублей, то выплатит долг за 4 года. Если по 587 250 рублей, то за 2 года. Найдите а.

18.        Найдите все значения а, при каждом из которых уравнение 8х⁶ + 4х ² — (3х + 5а)³ + 6х + 10а

не имеет корней.

19.        В роте два взвода, в первом взводе солдат меньше, чем во втором, но больше, чем 46, а вместе солдат меньше, чем 111. Командир знает, что роту можно построить по несколько человек в ряд так, что в каждом ряду будет одинаковое число солдат, больше 8, и при этом ни в каком ряду не будет солдат из двух разных взводов.

а) Сколько солдат в первом взводе и сколько во втором? Приведите хотя бы один пример.

б) Можно ли построить роту указанным способом по 13 солдат в одном ряду?

в) Сколько в роте может быть солдат?

ВАРИАНТ З

Часть 1

1.            В доме, в котором живёт Женя, один подъезд. На каждом этаже по восемь квартир. Женя живёт в квартире 87. На каком этаже живёт Женя?

2.            На диаграмме показано распределение выплавки меди в 11 странах мира (в тысячах тонн) за 2006 год. Среди представленных стран первое место по выплавке меди занимала Папуа — Новая Гвинея, одиннадцатое место — Индия. Какое место занимал Узбекистан?

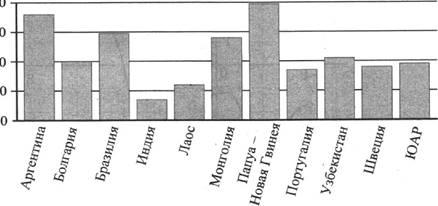200 150

100

50

З. Найдите площадь прямоугольной трапеции, вершины которой имеют координаты (З; 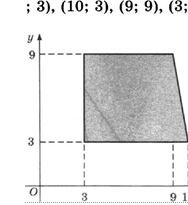З), (10; З), (9;

4.             В сборнике билетов по истории всего 50 билетов, в 13 из них встречается вопрос о Великой Отечественной войне. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос о Великой Отечественной войне.

5.             Найдите корень уравнения

9х+2 8х-4

6.             Угол А четырёхугольника ABCD, вписанного в окружность, равен 25 ⁰ . Найдите угол С четырёхугольника. Ответ дайте в градусах.

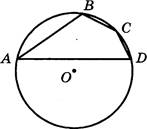
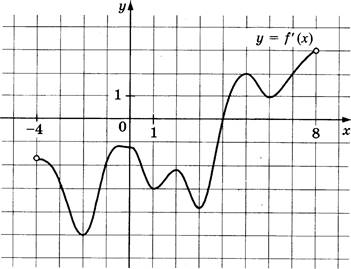
7.             На рисунке изображён график производной у = (х) функции f(x), определённой на- интервале (—4; 8). В какой точке отрезка [—3; 1] функция f(x) принимает наименьшее значение?

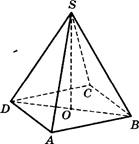
8.             В правильной четырёхугольной пирамиде SABCD точка О центр основания, S — вершина, SA = 10, BD = 16. Найдите длину отрезка SO.

Часть 2

9.             Найдите значение выражения      22

cos² 34 ⁰ + cos² 124 ⁰

10.        Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объём и давление связаны соотношением pV^{1 4} = const, где р (атм) давление в газе, — объём газа в литрах. Изначально объём газа равен 256 л, а его давление равно одной атмосфере. До какого объёма нужно сжать газ, чтобы давление в сосуде поднялось до 128 атмосфер? Ответ выразите в литрах.

11.        Плиточник должен уложить ЗОО м² плитки. Если он будет укладывать на 5 м² в день больше, чем запланировал, то закончит работу на 5 дней раньше, чем наметил. Сколько квадратных метров плитки в день планирует укладывать плиточник?

— Х² + 49

12.        Найдите точку максимума функции у =

13.        а) Решите уравнение tg² х + 5 tg х + 6 - 0.

б) Найдите все корни этого уравнения, принадлежащие отрезку

—2л; —— .

2

14.        Ребро SA пирамиды SABC перпендикулярно плоскости основания АВС.

а) Докажите, что высота пирамиды проведённая из точки А, делится плоскостью, проходящей через середины рёбер АД АС и SA,

пополам.

б) Найдите расстояние от вершины А до этой плоскости, если = мБ , Ав = АС = 5, вс = 245 .

15.        Решите неравенство logfX+11 (х + 1)⁴ + log2 (х + 1)² S 22 .

16.        Точки В1 и С1 лежат на сторонах соответственно АС и АВ треугольника АВС, причём АВ1 : ВIС = АС1 : СIВ . Прямые ВВ1 и СС1 пересекаются в точке О.

а) Докажите, что прямая АО делит пополам сторону ВС.

б) Найдите отношение площади четырёхугольника АВIОС1 к площади треугольника АВС, если известно, что АВ : В С —

17.        Тимофей хочет взять в кредит 1,1 млн рублей. Погашение кредита происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов. Ставка процента 10 ⁰/0 годовых. На какое минимальное количество лет может Тимофей взять кредит, чтобы ежегодные выплаты были не более 270 тысяч рублей?

18.        Найдите все значения а, при каждом из которых уравнение

64х⁶ + 4х² не имеет корней.

19.        Конечная последовательность щ, ф, состоит из п 23 не обязательно различных натуральных чисел, причём при всех натуральных К п —2 выполнено равенство ак+2 2а —4 —1.

а) Приведите пример такой последовательности при п = 5, в которой а5 = 4.

б) Может ли в такой последовательности некоторое натуральное число встретиться три раза?

в) При каком наибольшем п такая последовательность может состоять только из трёхзначных чисел?

ВАРИАНТ 4

Часть 1

1.            По тарифному плану «Просто как день» компания сотовой связи каждый вечер снимает со счёта абонента 18 рублей. Если на счету осталось меньше 18 рублей, то на следующее утро номер блокируют до пополнения счёта. Сегодня утром у Лизы на счету было 500 рублей. Сколько дней (включая сегодняшний) она сможет пользоваться телефоном, не пополняя счёт?

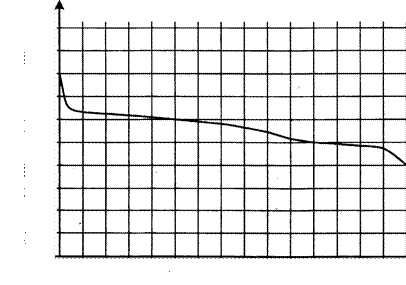
2.            При работе фонарика батарейка постепенно разряжается, и напряжение в электрической цепи фонарика падает. На рисунке показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечается время работы фонарик-а в часах, на вертикальной оси — напряжение в вольтах. Определите по рисунку, какое напряжение будет в цепи через 15 часов работы фонарика. Ответ дайте в вольтах.

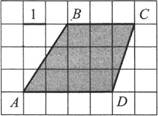З. Найдите площадь трапеции ABCD, изображённой на клетчатой бумаге с размером клетки 1х 1 (см. рис.).

4. 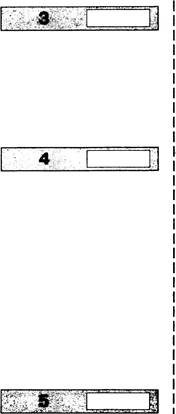            Павел Иванович совершает прогулку из точки А по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Найдите вероятность того, что Павел Иванович попадёт в точку G.

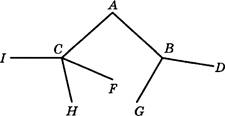
5.             Найдите корень уравнения log1 (5 — х) = —

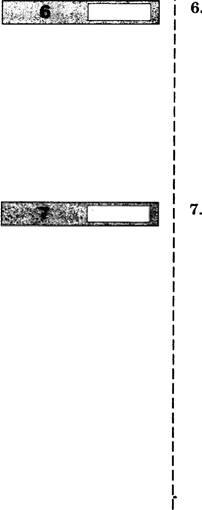
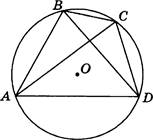Четырёхугольник ABCD вписан в окружность. Угол АВС равен 132 ⁰ , угол „4.BD равен 61 ⁰ . Найдите угол СМ). Ответ дайте в градусах.

На рисунке изображены график функции у= f(x) и десять точек на оси абсцисс: х1, х2, хз, . . . , х10. В скольких из этих точек производная Г(х) функции f(x) положительна?

8. Бетонный шар весит 0,5 т. Сколько тонн будет весить шар вдвое большего радиуса, сделанный из такого же бетона?

Часть 2

60

9.             Найдите значение выражения     

610g6 5

10.        Коэффициент полезного действия некоторого двигателя определяется формулой —  • 100 % . При каком значении температу-

ры нагревателя Т1 (в градусах Кельвина) КПД этого двигателя будет 80 ⁰/0 , если температура холодильника Т2 = 200 К?

11.        Брюки дороже рубашки на 30 ⁰/0 и дешевле пиджака на 22 ⁰/0 . На сколько процентов рубашка дешевле пиджака?

12.        Найдите наибольшее значение функции

у = 13х — 13tg х — 18

на отрезке О;

4

13.        а) Решите уравнение 5 • 4х² + 4х + 20-10х² + 4х -1 -7 -25х2+ 4х - 0 .

б) Найдите все корни этого уравнения, принадлежащие отрезку

14.        В правильной треугольной призме АВСА1В1С1 сторона основания АВ = 745 , а боковое ребро АА1 = 8.

а) Докажите, что плоскость ВСА1 перпендикулярна плоскости, проходящей через ребро АД и середину ребра ЦС1.

б) Найдите тангенс угла между плоскостями ВСА1 и ВВ1С1.

20

15.        Решите неравенство х +

16.        На сторонах АС и ВС треугольника АВС вне треугольника построены квадраты ACDE и ВМС. Точка М — середина стороны АВ.

а) Докажите, что СМ = — Dk .

б) Найдите расстояния от точки М до центров квадратов, если АС = 14, ВС = 16 и ИСВ = 150⁰ .

В двух областях есть по 50 рабочих, каждый из которых готов трудиться по 10 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,2 кг алюминия или 0,1 кг никеля. Во второй области для добычи х кг алюминия в день требуется х ² человеко-часов труда, а для добычи у кг никеля в день требуется у ² человеко-часов труда.

Обе области поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 1 кг алюминия приходится 2 кг никеля. При этом области договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?

18.       Найдите все значения К, при каждом из которых уравнение

= 2 имеет хотя бы одно решение на отрезке

sin t — cos t

О;

2

19.       Три различных натуральных числа являются длинами сторон некоторого тупоугольного треугольника.

а) Может ли отношение большего из этих чисел к меньшему из з них быть равно

2

б) Может ли отношение большего из этих чисел к меньшему из них быть равно — ?

в) Какое наименьшее значение может принимать отношение большего из этих чисел к меньшему из них, если известно, что среднее по величине число равно 18?

ВАРИАНТ 5

Часть 1

1.            Железнодорожный билет для взрослого стоит 220 рублей. Стоимость билета для школьника составляет 50 ⁰/0 от стоимости билета для взрослого. Группа состоит из 16 школьников и З взрослых. Сколько рублей стоят билеты на всю группу?

2.            На графике, изображённом на рисунке, представлено изменение биржевой стоимости акций газодобывающей компании в первые две недели ноября. 2 ноября бизнесмен приобрел 10 акций этой компании. Шесть из них он продал 6 ноября, а 13 ноября — остальные 4. Сколько рублей потерял бизнесмен в результате этих операций?

2100. ' '

1800

1500

1200

900 600 зоо

1 2 3 4 5 6 7 8 9 10 11 1213 14

З. Наидите площадь трапеции, вершинами которой являются точки с координатами (1; 6), (7; 6), (4; 1), (2; 1).

4.             
В среднем из 150 карманных фонариков три неисправных. Найдите вероятность купить работающий фонарик.

5.              Найдите корень уравнения х ² — 15 = (х — 15)2

6.              Концы отрезка АВ лежат по разные стороны от прямой l. Расстояние от точки А до прямой I равно 7, а расстояние от точки В до прямой I равно 13. Найдите расстояние от середины отрезка АВ до прямой l.

7.              На рисунке изображены график функции у = f(x) и касательная к нему в точке с абсциссой хо. Найдите значение производной функции f(x) в точке хо.

8.

Найдите объём куба.

Часть 2

9.             Вычислите значение выражения             ⁷ + 4910g7 Jii

10.        Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой = • 100 ⁰/0 , где — температура

нагревателя (в градусах Кельвина), Т2 температура холодильника (в градусах Кельвина). При какой температуре нагревателя 7'1 КПД двигателя будет 15 ⁰/0, если температура холодильника Т2 = 340 ⁰ К? Ответ выразите в градусах Кельвина.

11.        Из пункта А круговой трассы, длина которой равна 30 км, одновременно в одном направлении стартовали два автомобилиста. Скорость первого равна 92 км/ч, скорость второго — 77 км/ч. Через сколько минут первый автомобилист будет опережать

второго ровно на 1 круг?

12.        Найдите          наибольшее значение       функции

у = 6sinx — 345х + 0, 5Ј5п + 6 на отрезке О;

2

13.        а) Решите уравнение 6 sin² х + 7 cos х — 7 = О.

б) Найдите все корни этого уравнения, принадлежащие отрезку

14.        В прямоугольном параллелепипеде ABCDA1B1CID1 известны длины рёбер „4,41 = 7, АВ = 16, АО = 6. Точка К — середина ребра ClDl.

а) Докажите, что плоскость, проходящая через точку В перпендикулярно прямой АК, пересекает отрезок ДК .

б) Найдите тангенс угла между этой плоскостью и плоскостью АВС.

28х ² + 2х -10

15.        Решите неравенство х^з + 6х ² +     х-5

16.        На катетах АС и ВС прямоугольного треугольника АВС вне треугольника построены квадраты ACDE и ВМС. Точка М — середина гипотенузы АВ, Н — точка пересечения прямых СМ и Dk.

а) Докажите, что СМ Dk .

б) Найдите МН, если известно, что катеты треугольника АВС равны 130 и 312.

17.        15-го января планируется взять кредит в банке на 18 месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 2 ⁰/0 по сравнению с концом предыдущего месяца;  со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.

Сколько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь срок кредитования?

18.        Найдите все значения а, при каждом из которых уравнение 10-0,2^{1 х} — а — 5 ^x + 2а = О, 04-х имеет ровно два неотрицательных решения.

19.        Конечная возрастающая последовательность  состоит из п 23 не обязательно различных натуральных чисел, причём при всех натуральных К п —2 выполнено равенство Зак+2 = 5а - 2ак .

а) Приведите пример такой последовательности при п = 4 .

б) Может ли в такой последовательности при некотором п З ВЫПОЛНЯТЬСЯ равенство ап = 302 — 201 ?

в) Какое наименьшее значение может принимать а1 , если  = 667?

ВАРИАНТ 6

                                                                       Часть 1       

1.            Поезд Екатеринбург—Москва отправляется в 7:23, а прибывает в 9:23 на следующий день (время московское). Сколько часов поезд находится в пути?

2.            На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода осадков не было,

4,5

4,0

3,5

3,0

2,5

2,0

1,5

1,0

0,5

0,0

8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

З.       На клетчатой бумаге с размером клетки 1х1 изображён равносторонний треугольник. Найдите радиус описанной около него окружности.

4.             В среднем из каждых 50 поступивших в продажу аккумуляторов 48 аккумуляторов заряжены. Найдите вероятность того, что купленный аккумулятор не заряжен.

5.             Найдите корень уравнения log8 2^{7х 8}

6.             В треугольнике АВС АС = ВС     12, tgA           Найдите высоту сн.

7.             На рисунке изображён график функции у = f(x), определённой на интервале (—10; 2). Найдите количество точек, в которых касательная к графику функции параллельна прямой у - -20.

8.             Объём параллелепипеда ABCDAIBICID1 равен З. Найдите объём треугольной пирамиды ADICB1.

Часть 2

9.             Найдите значение выражения 7 • 5logs 2

10.        При температуре 0⁰С рельс имеет длину = 25 метров, а зазор между соседними рельсами равен 12 мм. При возрастании температуры происходит тепловое расширение рельса, и его длина будет меняться по закону l(t) = lo (1 + ос • t) , где = 1,2 10 ⁵ ( ^ос)-1 коэффициент теплового расширения, t температура (в градусах Цельсия). При какой температуре зазор между рельсами исчезнет? (Ответ выразите в градусах Цельсия.)

11.        Два человека отправляются из одного и того же места на прогулку до опушки леса, находящейся в 4,3 км от места отправления. Один идёт со скоростью 4 км/ч, а другой со скоростью 4,6 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча? Ответ дайте в километрах.

12.       

13.        а) Решите уравнение           =

б) Найдите все корни этого уравнения, принадлежащие отрезку

— Зп; — 2

14.        Основание прямой четырёхугольной призмы ABCDAIB1CID1 прямоугольник ABCD, в котором АВ = 12, „40 = . Расстояние между прямыми АС и BID1 равно 5.

а) Докажите, что плоскость, проходящая через точку D перпендикулярно прямой ВЦ , делит отрезок BD в отношении

1                                                 : 7, считая от вершины D1.

б) Найдите косинус угла между плоскостью, проходящей через точку D перпендикулярно прямой Щ, и плоскостью основания призмы.

2                                                 З

15.        Решите неравенство

Х — 12Х + 35 Х -17х+ 70

16.        Пятиугольник ABCDE вписан в окружность. Из вершины А опуЩеНЫ перпендикуляры АР, АН, АР и AQ на прямые DE, ВЕ, CD и ВС соответственно.

а) Докажите, что ZFAH = ZPAQ.

б) Найдите АН, если АР = а, АР = Ь и „4Q = с.

17.        В двух областях есть по 250 рабочих, каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,2 кг алюминия или 0,1 кг никеля. Во второй области для добычи х кг алюминия в день требуется х² человеко-часов труда, а для добычи у кг никеля в день требуется у ² человеко-часов труда.

Для нужд промышленности можно использовать или алюминий, или никель, причём 1 кг алюминия можно заменить 1 кг никеля. Какую наибольшую массу металлов можно добыть в двух областях суммарно для нужд промышленности?

18.        Найдите все значения а, при каждом из которых множество ре-

а — (а ² — 2а — 3)cosx + 4 шений неравенства  < 1 содержит отрезок

sin² х + а² + 1

19.        Можно ли привести пример пяти различных натуральных чисел, произведение которых равно 312 и

а) пять;

б) четыре;

в) три из них образуют геометрическую прогрессию?

Часть 1

1.            Установка двух счётчиков воды (холодной и горячей) стоит 3500 рублей. До установки счётчиков за воду платили 1700 рублей ежемесячно. После установки счётчиков ежемесячная оплата воды стала составлять 1100 рублей. Через какое наименьшее количество месяцев экономия по оплате воды превысит затраты на установку счётчиков, если тарифы на воду не изменятся?

2.            На рисунке жирными точками показана цена тонны никеля на момент закрытия биржевых торгов во все рабочие дни с 6 по 20 мая 2009 года. По горизонтали указываются числа месяца, по вертикали — цена тонны никеля в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку разность между наибольшей и наименьшей ценой никеля на момент закрытия торгов в указанный период (в долларах США за тонну).

13 600 13 400

13 200

13 000

12 800

12 600

12 400

• 12 200 12 000

11 800

6 7 8 11 12 13 14 15 18 19 20

зо

З. На клетчатой бумаге изображён круг площадью 72. Найдите площадь заштрихованного сектора.

4.             Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,05. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,96. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,04. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.

5.             Найдите корень уравнедия (х      = -32.

6.             В треугольнике АВС АС = ВС 5, sin А — Найдите АВ .

7.             На рисунке изображён график функции у = f' (х) — производной функции f(x) , определённой на интервале (— З; 8) . Найдите точку минимума функции f(x) .

8.             Найдите объём многогранника, вершинами которого являются точки А, В, С, „41, С1 правильной треугольной призмы АВСАIВ1С1, площадь основания которой равна 4, а боковое ребро равно 9.

Вычислите log5135 — log55,4.

10.        Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора получена экспериментально: Т = То +bt + а е , где t время в минутах, То = 1450 К,

— 30 К/мин² , Ь = 180 К/мин. Известно, что при температуре нагревателя свыше 1600 К прибор может испортиться, поэтому его нужно отключить. Определите (в минутах), через какое наибольшее время после начала работы нужно отключить прибор.

11.        В сосуд, содержащий 10 литров 24-процентного водного раствора некоторого вещества, добавили 5 литров воды. Сколько процентов составит концентрация получившегося раствора?

12.        Найдите наибольшее значение функции у = 76х — 38 tg х —       + 87

на отрезке О;

з

13.        а) Решите уравнение 4sin ⁴ 2х + З cos 4х —1 = О .

б) Найдите все корни этого уравнения, принадлежащие отрезку

Зл л;

2

14.        В правильной треугольной пирамиде SABC с вершиной S, все рёбра которой равны 2, точка М — середина ребра АД точка О центр основания пирамиды, точка F делит отрезок SO в отношении З : 1, считая от вершины пирамиды.

а) Докажите, что прямая МЕ перпендикулярна прямой SC.

б) Найдите угол между плоскостью МВЕ и плоскостью АВС.

15.        Решите неравенство 9^{х з} — 9х 2 +9х 1 > 511.

16.        Окружность с центром О вписана в угол, равный 60 ⁰ . Окружность большего радиуса с центром 01 также вписана в этот угол и проходит через точку О.

а) Докажите, что радиус второй окружности вдвое больше радиуса первой.

б) Найдите длину общей хорды этих окружностей, если известно, что радиус первой окружности равен 2415 .

32

17.        В начале 2001 года Алексей приобрёл ценную бумагу за 19 ООО рублей. В конце каждого года цена бумаги возрастает на 3000 рублей. В начале любого года Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 10 ⁰/0. В начале какого года Алексей должен продать ценную бумагу, чтобы через пятнадцать лет после покупки этой бумаги сумма на банковском счёте была наибольшей?

18.        При каких значениях а уравнение х² — 4х —5 — За = х — al — 1 имеет ровно три корня?

19.        Красный карандаш стоит 17 рублей, синий 13 рублей. Нужно купить карандаши, имея всего 495 рублей и соблюдая дополнительное условие: число синих карандашей не должно отличаться от числа красных карандашей больше чем на пять.

а) Можно ли купить при таких условиях 32 карандаша?

б) Можно ли купить при таких условиях 35 карандашей?

в) Какое наибольшее число карандашей можно купить при таких условиях?

                                                                       ВАРИАНТ 8       

Часть 1

1.            Для приготовления яблочного варенья на 1 кг яблок нужно 1,2 кг сахара. Сколько килограммовых упаковок сахара нужно купить, чтобы сварить варенье из 26 кг яблок?

2.            На диаграмме показан средний балл участников 10 стран в тестировании учащихся 8-го класса по естествознанию в 2007 году (по 1000балльной шкале). Среди указанных стран второе место принадлежит Великобритании. Определите, какое место занимает Россия.

560

550

540

530

520

510

500

490

480

З. На клетчатой бумаге с размером клетки 1х1 изображён угол. Найдите его градусную величину.

4.             В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что решка выпадет ровно один раз.

5.             Найдите корень уравнения  = 9 .

6.             В треугольнике АВС угол А равен 56⁰ , углы В и С — острые, высоты ВИ) и СЕ пересекаются в точке О. Найдите угол DOE. Ответ дайте в градусах.

7.             На рисунке изображён график функции у = f(x) , определённой на интервале (— 6; 6) . Найдите количество решений уравнения

f '(х) = О на отрезке

8.             Шар, объём которого равен л, вписан в куб. Найдите объём куба.

Часть 2

9.             Найдите значение выражения 200 cos   $6.

10.        Рейтинг R интернет-магазина вычисляется по формуле

О, 02k

где т —— средняя оценка мага-

зина покупателями, оценка магазина, данная экспертами, К — число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина, если число покупателей, оценивших магазин, равно 26, их средняя оценка равна 0,68, а оценка экспертов равна 0,32.

11.        Расстояние между городами А и В равно 440 км. Из города А в город В выехал первый автомобиль, а через два часа после этого навстречу ему из города В выехал со скоростью 90 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 260 км от города А. Ответ дайте в км/ч.

12.        Найдите наибольшее значение функции у = ln(x + 5) ⁵ — 5х на от-

резке  .

13.        а) Решите уравнение 19 • 4 ^x - 5 . 2 ^х + ² + 1 = 0 .

б) Укажите корни этого уравнения, принадлежащие отрезку

14.        В правильной треугольной призме АВСА1ВIС1 все рёбра равны 1.

а) Докажите, что прямая АД параллельна прямой, проходящей через середины отрезков АС и ВС1 .

б) Найдите косинус угла между прямыми АВ1 и ВС1.

15.        Решите неравенство 1 + log6(4 — х) log6 (16 — х²

16.        На сторонах АС и ВС треугольника АВС вне треугольника построены квадраты ACDE и ВРКС. Точка М середина стороны АВ.

а) Докажите, что СМ = — Dk .

б) Найдите расстояния от точки М до центров квадратов, если АС = 6, ВС = 10 и ZACB = 30⁰ .

17.        У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свеклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет ЗОО ц/га, а на втором 200 ц/га. Урожайность свеклы на первом поле составляет 200 ц/га, а на втором — ЗОО ц/га.

Фермер может продавать картофель по цене 10 ООО руб. за центнер, а свеклу по цене 13 ООО руб. за центнер. Какой наибольший доход может получить фермер?

18.        Найдите все значения а, при каждом из которых уравнение +21 +3 х² +4х +13 +21 имеет хотя бы один корень.

19.        а) Приведите пример такого натурального числа п , что числа п и (п + 16)² дают одинаковый остаток при делении на 200.

б) Сколько существует трёхзначных чисел п с указанным в пункте а свойством?

в) Сколько существует двузначных чисел т , для каждого из которых существует ровно 36 трёхзначных чисел п , таких, что п ² и (п + т) дают одинаковый остаток при делении на 200.

ВАРИАНТ 9

Часть 1

1.            Для ремонта квартиры купили 42 рулона обоев. Какое наименьшее количество пачек обойного клея нужно купить, если одна пачка клея рассчитана на 8 рулонов?

2.            На диаграмме показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются номера месяцев, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько месяцев второго полугодия 1999 года средняя температура была ниже 15 ^о с.

24,0

20,0'

16,0

12,0

- 12,0

                                               З,               Найдите площадь трапеции с вершинами (1; 1),(10; 4),

                                            0 1 2 3           10 х

4.             В случайном эксперименте бросают две игральные кости (кубика). Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.

5.             Найдите корень уравнения 32^{х з}

6.             В треугольнике АВС угол С равен 90 ⁰ , cos А            Найдите sin В.

7.             На рисунке изображён график функции у f(x), определённой на интервале (—5; 9). Найдите количество точек, в которых производная функции f(x) равна О.

8.             Диагональ правильной четырёхугольной призмы наклонена к плоскости основания под углом 30 ⁰ . Боковое ребро равно З. Найдите диагональ призмы.

Часть 2

9.             Найдите значение выражения 9 — 43 —

10.        Ёмкость высоковольтного конденсатора в телевизоре С = З • 10-6 Ф. Параллельно с конденсатором подключён резистор с сопротивлением R = 5 • 10⁶ Ом. Во время работы телевизора напряжение на конденсаторе Uo = 9 кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое с

выражением t = aRC log2 (с), где = 1,1  — постоянная. ом • Ф

Определите напряжение на конденсаторе, если после выключения телевизора прошло 33 секунды. Ответ дайте в кВ (киловольтах).

11.        Первая труба наполняет бак объёмом 600 литров, а вторая труба — бак объёмом 900 литров. Известно, что одна из труб пропускает в минуту на З л воды больше, чем другая. Сколько литров воды в минуту пропускает вторая труба, если баки были наполнены за одно и то же время?

12.        Найдите наименьшее значение функции у = е2х — 5е^х — 2 на отрезке

13.        а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку

л;

2

14.        Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Расстояние между этими хордами равно 730 .

а) Докажите, что центры оснований цилиндра лежат по разные стороны от этой плоскости.

б) Найдите угол между этой плоскостью и плоскостью основания цилиндра.

15.        Решите неравенство 2^х + З • 2-х < 4 .

16.        На катетах АС и ВС прямоугольного треугольника АВС вне треугольника построены квадраты ACDE и ВМС. Точка М — середина гипотенузы АД Н — точка пересечения прямых СМ и Dk.

а) Докажите, что СМ Dk.

б) Найдите МН, если известно, что катеты треугольника АВС равны 30 и 40.

17.        15-го января планируется взять кредит в банке на сумму 2,4 млн рублей на 24 месяца. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 3 ⁰/0 по сравнению с концом предыдущего месяца;  со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Какую сумму нужно выплатить банку за первые 12 месяцев?

18.        Найдите все значения а, при каждом из которых уравнение а ² +7 х + 1! +5 х ² +2х +5 = 2а + 31х — 4а +11

имеет хотя бы один корень.

19.        Имеется 8 карточек. На них записывают по одному каждое из чисел —1, 2, 4, —6, 7, —8, —10, 12. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел —1, 2, 4, —6, 7, —8, —10, 12. После этого числа на каждой карточке складывают, а полученные восемь сумм перемножают.

а) Может ли в результате получиться О?

б) Может ли в результате получиться 1?

в) Какое наименьшее целое неотрицательное число может в результате получиться?

ВАРИАНТ 1 о

                                      Часть 1   

В розницу один номер еженедельного журнала «Репортаж» стоит 26 руб., а полугодовая подписка на этот журнал стоит 590 руб. За полгода выходит 25 номеров журнала. Сколько рублей сэкономит Иванов за полгода, если не будет покупать каждый номер журнала отдельно, а оформит подписку?

На диаграмме показана средняя температура воздуха в Нижнем Новгороде за каждый месяц 1994 года. По горизонтали указываются номера месяцев, по вертикали средняя температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев с отрицательной средней температурой в 1994 году в Нижнем Новгороде.

З. На клетчатой бумаге с размером клетки 1х1 отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС.

4.             В случайном эксперименте симметричную монету бросают четыреэкды. Найдите вероятность того, что орёл выпадет ровно три раза.

5.             Найдите корень уравнения log3 (2 — х) = 2.

6.             В прямоугольном треугольнике угол между высотой и медианой, проведёнными из вершины прямого угла, равен 28⁰ . Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.

7.             На рисунке изображён график у = f' (х) производной функции f(x), определённой на интервале (—4; 10). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой у = —2х + 16 или совпадает с ней.

8.             Найдите объём многогранника, изображённого на рисунке (все двугранные углы прямые).

Часть 2

4 cos 146 ⁰

9.             Найдите значение выражения cos 34 ⁰

10.        Для определения эффективной температуры звёзд используют закон Стефана—Больцмана, согласно которому мощность излучения нагретого тела Р, измеряемая в ваттах, прямо пропорциональна площади его поверхности и четвёртой степени температуры:

Р = 6ST⁴ , где б = 8 вт         — постоянная, площадь S измем2 .к4

ряется в квадратных метрах, а температура Т — в градусах Кельвина. Известно, что некоторая звезда имеет площадь

1

• 10²¹ м ² , а излучаемая ею мощность Р равна  Вт. 256

Определите температуру этой звезды. Ответ выразите в градусах Кельвина.

11.        Игорь и Паша могут покрасить забор за 30 часов. Паша и Володя могут покрасить этот же забор за 36 часов, а Володя и Игорь — за 45 часов. За сколько часов мальчики покрасят забор, работая втроём?

12.        Найдите точку минимума функции у = х ² — 14х + 20 lnx 6.

13.        а) Решите уравнение 2 sin⁴ х + З cos 2х + 1 = О .

б) Найдите все корни этого уравнения, принадлежащие отрезку

14.        Площадь боковой поверхности правильной четырёхугольной пирамиды SABCD с основанием ABCD равна 108, а площадь полной поверхности этой пирамиды равна 144,

а) Докажите, что угол между плоскостью SAC и плоскостью, проходящей через вершину S этой пирамиды, середину стороны АВ и центр основания, равен 45 ⁰ .

б) Найдите площадь сечения пирамиды плоскостью SAC .

ln х —2х

15.        Решите неравенство 7        42—х)

16.        Медианы АА1, ВВ1 и СС1 треугольника АВС пересекаются в точке М. Точки „42, В2 и (22 — середины отрезков МА, МВ и МС соответственно.

а) Докажите, что площадь шестиугольника А1В2СIА2ВIС2 вдвое меньше площади треугольника АВС.

б) Найдите сумму квадратов всех сторон этого шестиугольника, если известно, что АВ = 5, ВС = 8 и АС = 10.

17.        1 января 2015 года Александр Сергеевич взял в банке 1,1 млн рублей в кредит. Схема выплаты кредита следующая — 1-го числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (то есть увеличивает долг на 194), затем Александр Сергеевич переводит в банк платёж. На какое минимальное количество месяцев Александр Сергеевич может взять кредит, чтобы ежемесячные выплаты были не более 275 тыс. рублей?

18.        Найдите все значения а, при каждом из которых уравнение 1х — а² + + а + 21 + lX — 0² + За — 2а — З имеет корни, но ни один из них не принадлежит интервалу (4; 19).

19.        Возрастающая конечная арифметическая прогрессия состоит из различных целых неотрицательных чисел. Математик вычислил разность между квадратом суммы всех членов прогрессии и суммой их квадратов. Затем математик добавил к этой прогрессии следующий её член и снова вычислил такую же разность.

а) Приведите пример такой прогрессии, если во второй раз разность оказалась на 48 больше, чем в первый раз.

б) Во второй раз разность оказалась на 1440 больше, чем в первый раз. Могла ли прогрессия сначала состоять из 12 членов?

в) Во второй раз разность оказалась на 1440 больше, чем в первый раз. Какое наибольшее количество членов могло быть в прогрессии сначала?

ОТВЕТЫ

Вариант 1

Вариант 2

                     Вариант З       

4

Вариант 5

Вариант 6

7

Вариант 8

Вариант 9

10

РЕШЕНИЕ ЗАДАНИЙ

Вариант 10 Часть 2

13. а) Решите уравнение 2sin ⁴ х + З cos 2х + 1 = О.

б) Найдите все корни этого уравнения, принадлежащие отрезку [п; Зп].

Решение.

а) Воспользуемся формулой sin ² х = 1 — cos 2х

2

Из неё следует, что sin ⁴ х — — cos² 2х — 2 cos 2х + 1

Поэтому уравнение можно преобразовать так:

1

— cos ² 2х — cos 2х + — + З cos 2х + 1 — О 2 cos ² 2х + 4cos 2х +3 = О.

Сделаем замену t = cos 2х . Получим

t = —1 или t = cos2x = —1 или cos2x = —3 .

Уравнение cos 2х — —3 не имеет решений. Из уравнения cos 2х — —1 получаем

2х = п + 2лп п eZ. n ez

2

б) При помощи тригонометрической окружности отберём корни, принадлежащие за-

данному отрезку.

2

Зл

Ответ.n e z•, б)

                                                                                                                                                               2       2

14. Площадь боковой поверхности правильной четырёхугольной пирамиды SABCD с основанием ABCD равна 108, а площадь полной поверхности этой пирамиды равна 144.

а) Докажите, что угол между плоскостью SAC и плоскостью, проходящей через вершину S этой пирамиды, середину стороны АВ и центр основания, равен 45 ⁰ .

б) Найдите площадь сечения пирамиды плоскостью SAC .

Решение.

Площадь основания пирамиды равна 144 — 108 = 36, поэтому АВ = 6.

          Площадь боковой грани равна             27.

4

,srvf • АВ

        Пусть SM — высота грани SAB. Тогда SSAB                   = SM • З = 27, поэтому SM = 9.

2

а) Пусть SH — высота пирамиды. Тогда Н середина основания пирамиды. Значит, SH — прямая, по которой пересекаются данные плоскости. Прямая SH перпендикулярна любой прямой, лежащей в плоскости основания пирамиды, в том числе и прямым АН и МН. Значит, угол между плоскостями SAC и SMH — это угол АНМ, который равен 45⁰ .

          6) Имеем            = srvf ² - МН ² = dii = 6Ji .

            Тогда SSAC• АС = 60 •          = 36 .

Ответ: б) 36.

ln х

15.        Решите неравенство 7x)ln7

Решение.

 Преобразуем неравенство:

ln

^ln7

откуда получаем, что

Ответ.

16.        Медианы АА1, ВВ1 и СС1 треугольника АВС пересекаются в точке М. Точки „42, В2 и — середины отрезков МА, МВ и МС соответственно.

а) Докажите, что площадь шестиугольника А1В2С1А2В1С2 вдвое меньше площади треугольника АВС.

б) Найдите сумму квадратов всех сторон этого шестиугольника, если известно, что 5, ВС = 8 и АС = 10.

Решение:

а) Площадь треугольника А1МВ2 в два раза меньше площади треугольника „41 МВ, поскольку МВ = 2МВ2, а высота, проведённая из вершйны „41, у этих треугольников общая:

                                                                                                                                                              амв                       АIМВ2 •

Аналогично получаем ещё 5 равенств:

                        А мс                  АМС2 ' Ц МС        СIМА             qn,fA2 стмвг •

Складывая эти равенства почленно, получаем

                                                                                                                                                      АВС                     АIС2В1А2С1В2 •

б) Обозначим длины сторон ВС, АС, АВ треугольника АВС через а, Ь, с.

Докажем, что квадрат медианы АА1 равен — 2b² + 28 — а

Для доказательства на продолжении отрезка „4,41 за точку „41 отложим отрезок А1Р = АА1. Получим параллелограмм АСРВ со сторонами АС = РВ = Ь и АВ = СР = с и диагоналями ВС = а и АР = 2АА1. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон:

2b² + 2с ² = а ² + 4,4х41² , откуда АА+28 - а

         Аналогично доказывается, что ВВ1²         2а ² + 2с ² — b²20 ² + 2b ²

Отрезок СIА2 — средняя линия треугольника АВМ, значит,

— вц !вв1.

Рассуждая аналогично, мы получим, что стороны шестиугольника втрое меньше медиан треугольника АВС: В2С1 = В1С2 = — АД, АД = АД = ! СС1 . Следовательно, сумма з

квадратов сторон шестиугольника равна

2. (вс + ас: + д в;) = —(АА² + вв: + сс:)

                                  • (28 + 28 -а ² +     +28

2) 61 (0 ² + b² + с2).

Подставляя в эту формулу длины сторон треугольника АВС, получаем ответ: сумма 63 квадратов сторон шестиугольника равна

2

63 Ответ:

2

17.        1 января 2015 года Александр Сергеевич взял в банке 1,1 млн рублей в кредит. Схема выплаты кредита следующая 1 числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (то есть увеличивает долг на 1 ⁰/0), затем Александр Сергеевич переводит в банк платёж. На какое минимальное количество месяцев Александр Сергеевич может взять кредит, чтобы ежемесячные выплаты были не более 275 тыс. рублей?

Решение:           

Заметим, что за 4 месяца Александр Сергеевич выплатит 1,1 млн рублей. Таким образом, он не покроет долг с процентами.

Каждый месяц долг увеличивается не более, чем на 1 100 ООО • 0,01 — 11 ООО рублей. Значит, за пять месяцев Александр Сергеевич должен будет выплатить не более 1 100 ООО + 5•11 ООО = 1 155 ООО рублей, что менее чем 5• 275 ООО = 1 375 ООО рублей. Таким образом, Александр Сергеевич сможет выплатить кредит за 5 месяцев.

Ответ: 5.

18.        Найдите          все      значения       а,         при     каждом         из        которых        уравнение

- 20 -3 имеет корни, но ни один из них не принадлежит

интервалу (4; 19).

Решение:

Разность выражений, стоящих под знаками модуля, совпадает с правой частью уравнения:

х— а² + За —1

Сделаем замену: т — х — а² + За — 1, п —— Х — 0 ²

Тогда уравнение примет вид:

Это равносильно условию п О т . Получаем

х—а ² + а + За — 1 ;

а² — За  —а —2.

Уравнение имеет корни, ни один из которых не принадлежит интервалу (4; 19), только если правая граница отрезка решений не больше 4 или левая граница не меньше 19.

Получаем

                        -0-2,             

Ответ: 1,5 а S З; а 2 6 .

19. Возрастающая конечная арифметическая прогрессия состоит из различных целых неотрицательных чисел. Математик вычислил разность между квадратом суммы всех членов прогрессии и суммой их квадратов. Затем математик добавил к этой прогрессии следующий её член и снова вычислил такую же разность.

а) Приведите пример такой прогрессии, если во второй раз разность оказалась на 48 больше, чем в первый раз.

б) Во второй раз разность оказалась на 1440 больше, чем в первый раз. Могла ли прогрессия сначала состоять из 12 членов?

в) Во второй раз разность оказалась на 1440 больше, чем в первый раз. Какое наибольшее количество членов могло быть в прогрессии сначала?

Решение.

 а) Пример: 1, 2, З. Разность квадрата суммы и суммы квадратов равна 36 — 14 = 22.  Если добавить число 4, то разность будет равна 100 — 30 = 70, что ровно на 48 больше, чем было.

б) Обозначим члены прогрессии ар аа . Тогда разность, вычисленная математиком в первый раз, равна

+20201.

Когда к прогрессии добавили член а то вычисленная во второй раз разность отличается от первой дополнительным слагаемым

                       + nd

где d — разность прогрессии.

Из условия следует, что а1 О и d 1 , поэтому

                                                   (01 +             + (п — 1)           п ² (п 1) .

Получаем неравенство п ² (п —1) 1440 ,

откуда п 11 . Значит, 12 членов в начальной прогрессии быть не может.

в) Из равенства (Щ + + (п — 1) = 1440 следует, что п является делителем числа 1440. Значит, п * 11 .

Если п = 10, получаем

(Щ  + 9d) = 144.

Если d 2 , то левая часть не меньше чем 90d² > 90 • 4 =144 .

Следовательно, d = 1 . Получаем уравнение ц +2901 - 54

которое не имеет целых решений.

Если п = 9 , получаем

                                                              (01 +                 + 8d) = 160 .

Если d > 2 , то левая часть не меньше чем 72d² > 72 • 4 = 288 > 160 .

Следовательно, d = 1. Получаем уравнение

а: + 1301 — 44 = О,

которое не имеет целых решений. Если п = 8, получаем:

(щ + и) (201 + 7d) = 180 .

Если d 2 , то левая часть не меньше чем 56d ² > 56 • 4 = 224  180. Следовательно, d = 1. Получаем уравнение

Ц +2301 - 124 = о ,

которое имеет единственный натуральный корень 4.

       Значит, прогрессия из восьми чисел 4, 5, 6            11 удовлетворяет условию задачи.

Ответ: а) 1, 2, З; б) нет; в) 8.

Справочное изДание

Ященко И. В., Волчкевич М. А., Высоцкий И. Р., Гордин Р. К.,

Семёнов П. В., Косухин О. Н., Фёдоровых Д. А., Суздальцев А. И.,

Рязановский А. Р., Сергеев И. Н., Смирнов В. А., Хачатурян А. В., Шестаков С. А., Шноль Д. Э.

ЕГЭ

МАТЕМАТИКА

ПРОФИЛЬНЫЙ УРОВЕНЬ

ТИПОВЫЕ ТЕСТОВЫЕ ЗАДАНИЯ

Издательство «ЭКЗАМЕН»

Гигиенический сертификат

№ РОСС RU.11U№l.H00199 от 19.05.2016 г.

Главный редактор Л. Д. Лаппо Редактор И. М. Бокова

Технический редактор Л. В. Павлова

Корректоры Л. К. Корнилова, Н. Н. Якоапева Дизайн обложки Л. В. Демьянова

Компьютерная верстка К. А. Реутова

107045, Москва, Луков пер., д. 8. www.examen.biz

E-mail: по общим вопросам: info@examen.biz; по вопросам реализации: sale@examen.biz тел./факс 8 (495) 641-00-30 (многоканальный)

Общероссийский классификатор продукции ок 005-93, том 2; 953005— книги, брошюры, литература учебная

Отпечатано в соответствии с предоставленными материалами в 000 ”ИПК Парето-Принт", 170546, Тверская область Промышленная зона Боровлево- 1, комплекс УВА www.pareto-print.ru

По вопросам реализации обращаться по тел.: 8 (495) 641-00-30 (многоканальный).