С.А. Агалаков

Неравенства

Общие замечания о решении неравенств

1.          Решение неравенства целесообразно начинать с анализа ограничений на неизвестную величину, т.е. с анализа области допустимых значений (ОДЗ), иначе — области определения неравенства (ОО). Следует выписать эти ограничения в виде системы и найти ее решения.

2.          В конце решения любого неравенства необходимо выполнить проверку найденных решений, используя ОДЗ (ОО).

3.          Приступая к решению неравенства, следует помнить, что наиболее часто применяется способ разложения на простые множители.

4.          Решение дробного неравенства, начинается, как правило, с приведения всех дробей к общему знаменателю.

5.          Неравенства возводить в квадрат или любую другую четную степень можно только тогда, когда обе его части неотрицательны.

6.          Любые неравенства можно решать обобщенным методом интервалов, т. е. сначала решая уравнение (с проверкой корней), а затем вычисляя знаки соответствующей функции на интервалах ОДЗ.

Предполагается, что задание №17, в котором требуется решить неравенство, будет более легким, чем аналогичное задание С3 из ЕГЭ прошлых лет. Поэтому в этом разделе приведены только те задания С3 из вариантов ЕГЭ, которые содержат решение одного неравенства.

Рассмотрим пример выполнения задания №17 из демонстрационного варианта 2015 года.

Пример 2. Решите неравенство

log (29 log-₁₅xx)--log (2log15₂₅x-x) _{£ log25 9 .}

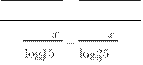
Решение. Неравенство определено при 0 x 2,x1. Преобразуем неравенство, приведя все логарифмы из левой части к основанию 5:

log (2₅ -x) - log (2₅ -x)

                                     log 9log5 ₅    loglog 15₅ 5  £ log25 9 ,

                                                                                                                                          2

log₅ èççççælog 15æççççèlog 9l5 1₅--log 25log 1515 1₅ ÷ø÷ö÷÷÷ ÷_÷ö÷÷÷ø £ log₂₅ 9 _, log (2⁵ -x) x

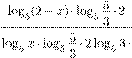 £ log₂₅ 9,

 £ log25 9 , loglog (25x5⋅2log-x5)3⋅ £ log25 9.

       Умножив преобразованное неравенство на 2^log₅ 3 > 0 , получаем:

.

 Вычислим знаки логарифмов с переменной при 0x1, 1 x 2 : log (2₅ -x) < 0 Û 0 < 2-x <1 Û 1< x > 2 , log₅x < 0 Û 0 < x <1.

Следовательно, на каждом из интервалов 0x1, 1x2 левая часть неравенства отрицательна, а правая положительна.

Таким образом, решение неравенства составляют все числа из интервалов (0; 1) и (1; 2).

Ответ: (0; 1), (1; 2).

Далее приведены задания из дидактических и тренировочных работ МИОО для подготовки к ЕГЭ 2010-2011 годов.

                                                                                                                                     3

Задания

x-1

6. 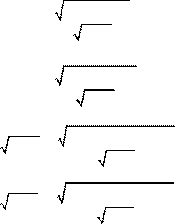    5-x < x3 -7x2 +14x -5 .

x -1

7.     log₂(x² + 4x) + log2₁ ^x₄ + 2 ³ log₂(x² + 3x - 4).

8.     .

9.     log (7_x - <x)          log_x (x³ - + - -6x²                                       14x 7) log (_x x-1) .

10.   log (5_x - <x)          log_x (x³ - + - -7x²                                       14x 5) log (_x x-1).

x +2           log x -5           _x .

                                                                                                                                          4

Ниже приведены задания из вариантов ЕГЭ 2010-2011 годов. Задания

Решите неравенства:

 .

 .

            2log (x² -2x)                2log (x² +5x)

£1. £1 .

17.  3log₅ çæççè5 +x²⁰-5^ö÷÷÷ø£ -9        2log_0,2 ^æçççè25-x¹⁰⁰-1^÷÷÷^öø.

18.  2log₄ ççèçæ256 +x¹⁰²⁴-4÷÷ø^ö÷£ 19-5log_0,25 ççè^æç16^{- 64}x ø÷^ö÷÷ .

19.  log 2x+(4-48x) £ log log 21          x . 20. loglog5x+(-3 2525x) £ log log 51  x . log

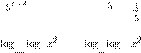                                                                                 1            7              1              17

                                                                      . 22. 17 ¹⁷               < 7    ⁷              .

Ответы к заданиям

1. -3 £x <-1, - <1 x £-0,5 . 2. -6 £x <-2, - <2 x £-1,5 .

3. 0 <x £1 , x =2, 3 £ <x                    4 , 4 <x £ 5 . 4. 0 <x £ 1 , x =3,

4 £ <x  5 , 5 <x £ 6. 5. 1< <x 2, 3 <x £ 7 . 6. 1< <x 2, 4 <x £ 5 . 7. 1 <x £ 17 . 8. - <2 x £ . 9. 1< <x 2, 3< <x 7 .

10. 1< <x 2, 4< <x 5 . 11. x<-2, x>6 . 12. 0 <x £ 0,5 ,

2 < x £ ⁴ 32 . 13. éê_ë-20;-9) È (1;2ú_ûù . 14. éê_ë-15;-6) (È -5;5ùú_û .

                                                                                                                                          5

15. (-1;0) (È 2;3ùú_û . 16. _ëéê-6;-5) (È 0;1). 17. (-¥;1) È ê_ê^é_ë³¹₆ ;+^¥÷÷_÷ø÷^ö .

18. (-¥;0) È ê_êé_ë256₆₃ ;+¥÷_÷ø^÷ö÷.     19. -8 £x <-4 , - < <-4 x      1,

-0,125 < <x 0 . 20. -25 £x <-3, - < <-3 x   1, - < <0,25 x 0 .

21. x <-1, x >1. 22. x <-1, x >1.