С.А. Агалаков

Уравнения

Общие замечания о решении уравнений

1.         Решение уравнения целесообразно начинать с анализа ограничений на неизвестную величину, т.е. с анализа области допустимых значений (ОДЗ), иначе — области определения уравнения (ОО). Следует выписать эти ограничения в виде системы (по крайней мере, в черновике). Возможно, полученные сведения помогут найти простое решение задачи.

2.         В конце решения любого уравнения необходимо выполнить проверку найденных корней, так как, кроме посторонних корней, возможны вычислительные ошибки. В простых случаях достаточно использовать подстановку корней в исходное уравнение. В этом случае указывать ограничения (ОДЗ или ОО) в чистовике не нужно. В более сложных ситуациях необходимо использовать ОДЗ (ОО), указывая в решении, какое именно ограничение использовалось.

3.         Приступая к решению уравнения, следует помнить, что наиболее часто применяется способ разложения на простые множители.

4.         Выполняя преобразования с корнями или и логарифмами, следует помнить, что: арифметический корень четной степени есть величина неотрица-

тельная, в частности, a² =|a |; выражение, стоящее под знаком логарифма, есть величина положи-

тельная, в частности, log_ab² = 2log_a b.

Рассмотрим пример выполнения задания №15 из демонстрационного варианта 2015 года.

Пример. а) Решите ^{уравнение} cos2x = 1- cosççççèæp2 - xö÷÷÷÷ø.

б) Найдите все корни этого уравнения, принадлежащие промежутку ^éêêë- ⁵2^p ;-p^ö÷÷÷÷ø .

          Решение. а) Так как cos2x = -1 2sin² x , cos^ççççèæ^p2 - x^÷÷÷ø^÷ö = sinx , то

2

1-2sin² x = -1     sinx , 2sin² x- =sinx 0, sinx sinx ^{-     ÷}÷^÷_÷ = 0 .

Корни уравнения: x =pn ,

x = -( 1)^{k p}+pk , n ZÎ , k ZÎ .

6

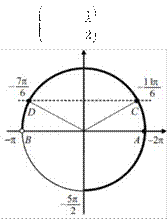
б) Корни уравнения sinx = 0 изобра-

жаются точками A и B , а корни уравнения sinx = точками C и D , промежуток

êêëé- 52p ;-pö÷÷÷÷ø изображается жирной дугой

(см. рис.). 

В указанном промежутке содержатся три корня уравнения: -2p ,

- + =-2p p     11p и - - =-p p  7p .

               6          6               6         6

Ответ: а) x =pn , x = -( 1)^{k p}+pk , n ZÎ , k ZÎ . 6

б) -2p , -11^p _, -7^p _.

                              6         6

Ниже приведены задания из дидактических и тренировочных работ, подготовленных    Московским        институтом                 открытого            образования (МИОО).

3

Задания

33.      Решите уравнение 6cos² x-7cosx- =5 0. Укажите корни, принадлежащие промежутку [-p p;2 ].

34.      Решите уравнение 4sin² x-12sinx+ =5 0 . Укажите корни, принадлежащие промежутку [-p p;2 ].

35.      Решите уравнение sinççççèæ₃2p - 2x÷÷÷÷øö = sinx и найдите корни, принадле-

éêêë32p p;52 ùúúû . жащие промежутку

æççççè32p + 2xö÷÷÷÷ø = cosx и найдите корни, принад36. Решите уравнение cos

éêêë52p ;4pùúúû . ^{лежащие промежутку}

37.     Решите уравнение cosx =ççççèæcos x2 -sin x2÷÷øö÷÷² -1 и найдите корни, при-

^{надлежащие промежутку} êêëép2 ;2pùúúû .

38.     Решите ^{уравнение} sinx + ^çççèçæcos ^x2 - sin ^x2^÷øè÷÷÷^öæç^çççcos ^x2 + sin ^x2^öø^÷÷÷÷ = 0 и

^{найдите корни, принадлежащие промежутку} êêëép;52pùúúû .

39.     Решите уравнение 2sin2x = 4cosx-sinx+1. Укажите корни, _{принадлежащие промежутку} êêëép p2 ;32 ùúúû .

40.     Решите уравнение sin2x = 2sinx- +cosx 1. Укажите корни, при^{надлежащие промежутку} êêëé-2p;- p2 ùúúû .

4

Далее приведены задания вида №15 единого государственного экзамена 2012-2014 годов.

Задания

41.  а) Решите уравнение 4cos² x -8sinx +1 = 0. б) Найдите все корни ^{этого уравнения, принадлежащие отрезку} êêëé-3p;- 32pùúúû .

42.  а) Решите уравнение 6sin² x + 5sinçççèæçp2 - xøö÷÷÷÷ - 2 = 0. б) Найдите все ^{корни этого уравнения, принадлежащие отрезку} êêëé-5p;- 72pùúúû .

43.  а) Решите уравнение cos2x + sin² x = 0,25 . б) Найдите все корни

^{этого уравнения, принадлежащие отрезку} êêëé3p;92pùúúû .

44.  а) Решите уравнение 4sin³ x = 3cosççççèæx - p2 ÷÷÷øö÷ . б) Найдите все корни

_{этого уравнения, принадлежащие отрезку} êêëé72p p;92 ùúúû .

45.  а) Решите уравнение 10^sinx = 2^sinx ⋅5^-cosx . б) Найдите все корни

^{этого уравнения, принадлежащие отрезку} êêëé- 52p ;-pùúúû .

46.  а) Решите уравнение 15^cosx = 3^cosx ⋅5^sinx . б) Найдите все корни этого уравнения, принадлежащие отрезку êêëé5p;132pùúúû .

5

æç3p - xö÷÷÷÷ø . б) Найдите все корни 47. а) Решите уравнение sin2x = 3 cosçççè 2 ^{этого уравнения, принадлежащие отрезку} éêë-3p p;-2 ùúû .

æçp + x÷÷øö÷÷ . б) Найдите все корни 48. а) Решите ^{уравнение} sin2x = sinçççè2 этого уравнения, принадлежащие отрезку êêëé- 72p;- 52pùúúû .

49.  а) Решите уравнение 3tg² x- 5 + =1 0 . б) Найдите все корни cosx

^{этого уравнения, принадлежащие отрезку} êêëé- 72p ;-2pùúúû .

50.  а) Решите уравнение 5tg² x + 3 + =3            0. б) Найдите все корни cosx

^{этого уравнения, принадлежащие отрезку} êêëé52p ;4pùúúû .

51. 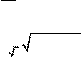 а) Решите уравнение 1+ log₂ (9x² + =5)      log ₂                       8x⁴ +14 . 

éêêë-1;89ùúúû .

б) Найдите все корни этого урав^{нения, принадлежащие отрезку}

52.  а). Решите уравнение 1+ log₃ (10x² + =1)    log ₃                       3x⁴ + 30 . 

б) Найдите все корни этого уравнения, принадлежащие отрезку éêêë-11 24 3; ùúúû .

6

53.  (2014). Решите ^{уравнение} cos2x + 2 sinççççèæp2 +xøö÷÷÷÷+ =1 0 . б) Ука^{жите корни этого уравнения, принадлежащие отрезку} êêëé-3p;- 32pùúúû .

² 3- 3 cos^çççèæç^p2 -^x÷÷øö^÷÷= 0 . б) Укажите

54.  (2014). Решите ^{уравнение} 2sin

^{корни этого уравнения, принадлежащие отрезку} êêëé-3p;- 32pùúúû .

55.  (2014). а) Решите _{уравнение} ^çæ ö^çççè ø25^÷÷÷÷^cosx +æ ö^çççè ø^ç25^÷÷÷÷^cosx = 2 . б) Укажите корни

^{этого уравнения, принадлежащие отрезку} êêëé-3p;- 32p ùúúû .

56.  (2014). а) Решите уравнение 9^sinx +9^-sinx = . б) Укажите корни ^{этого уравнения, принадлежащие отрезку} êêëé-3p;- 32p ùúúû .

57.  (2014). а) Решите уравнение  . б) Ука-

^{жите корни этого уравнения, принадлежащие отрезку} éêë2;3ùúû .

58.  (2014). Решите уравнение log₅ (2 - ^x) = log₂₅ x⁴ . б) Укажите корни этого уравнения, принадлежащие отрезку êêëé-log9 821 ;log 89 ùúúû .

Ответы к заданиям

33. x =±2^p+2pn ; -2p , 2p , 4p . 34. x ^{= -}( ¹)^{k p}+pk ; p , 5p . 35.

                      3                   3 3       3                         6             6 6

7

x = -( 1)k+1 p+pk , x = +p 2pn ; 11p , 5p . 36. x = -( 1)k p+pk ,

6   2          6          2          6 x = +^p pn ; 5p , 17p , 7p . 37. x =- +^p pn ; 3p , 7p . 38.

2 2 6 2 4 4 4 x =- +p pn ; 7p .

              4             4

39. x = +p 2pn , x = ±arccosçççèæç- 14÷ø÷ö÷÷ + 2pk ; p2 ,               arccosèæçççç- 14÷ö÷÷ø÷, 2

2p - arccosçç_ççèæ^- 1₄^÷ö÷^÷_÷ø . 40. x = -( 1)^{k+1 p}₆ +pk , x = 2pn ; -2p , -⁵₆p .

41. x ^{= -}( ¹)^{k p}+pk ; -11p . 42. x =±2^p+2pn ; -14p .

                            6                6                     3                  3

43. x =±^p+pn ; 10p , 11p , 13p . 44. x =±^p+pn , x =pn ; 13p ,

                     3              3       3       3                     3                           3

11p , 4p . 45. x =- +^p pn ; -9p , -5p . 46. x = +^p pn ; 21p , 25p .

3                             4               4        4                4             4       4

47.  x =_± 5^p+2pk , x =pk ; -3p , _-17p , -2p .

                      6                                        6

48.  x _{= +}^p 2pk , x _{= +}5^p 2pk , x = +p pn ; -7p , -19p ,-5p .

                 6                    6                    2                2         6        2

49.  x =±^p+2pn ; -7p . 50. x = +p p2 n ; 3p .

                     3                 3

51. ± -2,        ¹,¹ ;-¹,¹ .         52. ± ±3, 1 ;- -3, 1.              53. x _{= +}^p pn ,

                           2 2      2 2                                                          2

x =_± 3^p+2pn ; _-11p , _-5p , _-3p . 54. x =pk , x = -( 1)^{k p}+pk ;

               4                   4         2        2                                       3

2p , 7p , 8p , 3p . 55. x _{= +}^p pn ; _-5p , _-3p . 56. x =_±^p+2pn ,

           3      3                        2                2         2                    6

8

x =± 5^p+2pn ; -19p , -17p , -13p . 57. a) log 3 , log 4 ; б) log 3

               6                  6          6          6                                                   

. 58. a) -2 , 1; б). -2 .