Элективный курс

муниципальное бюджетное общеобразовательное учреждение

 «Советская средняя  школа №10»
 
 

 

 

Рабочая программа

 

по предмету   элективный курс по математике

«Математика вокруг нас» в 9 классе

 

 
Учителя   Дубинина С.В., Левкина В.А., Шкарубская Е.М.

 

 

Рассмотрено на заседании методического

объединения физико-математических      

 дисциплин

 

 

протокол № 1 от   28 августа  2014 года

 

 

 

2014-2015

 

 

 

 

 

 

 

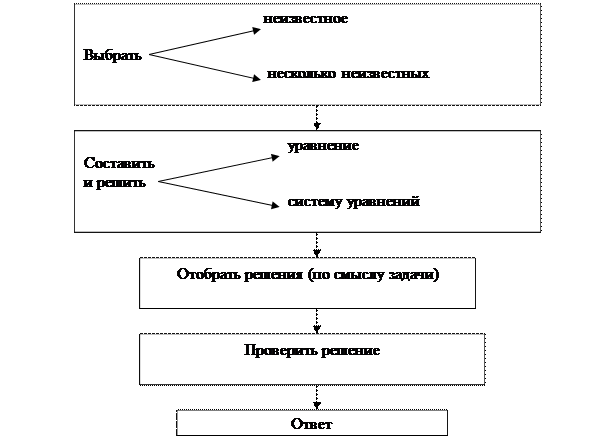
CТРУКТУРА   ДОКУМЕНТА

 Рабочая  программа по элективному курсу «   Математика вокруг нас9  класс включает разделы: пояснительную записку; основное содержание; требования к уровню подготовки обучающихся; список литературы; календарно- тематическое планирование.

 

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

 

Рабочая программа  по элективному курсу 9 класса составлена на основе:

- методических пособий;

1. Н.Я. Виленкин, А.Н.Виленкин, Г.С.Сурвилло и др. Алгебра: Учебное пособие для учащихся 9 кл. с углубленным изучением математики. Под ред. Н.Я.Виленкина.я газета «Математика», приложение к «1 сентября»,2004г. №17,№23,№36, 2005 г. №2,№15,2001г.

2.Кузнецова Л.В. и др. Сборник заданий для проведения письменного экзамена по алгебре за курс основной школы. - М.: Дрофа, 2002.
3. Кузнецова Л.В.  Суворова С.Б.  Сборник заданий для подготовки итоговой аттестации в 9 классе.   - М.:  Просвещение 2007.
4.  Барабанов, О. О. Задачи на проценты как проблемы словоупотребления. Математика в школе. —2003.
5. Башарин, Г. П. Начала финансовой математики. — М., 1997.
6.  Башарин, Г. П. Элементы финансовой математики. — М.: Математика (приложение к газете «Первое сентября»).№27— 1995.
7. Вигдорчик, Е., Нежданова, Т. Элементарная математика в экономике и бизнесе. — М., 1997.
8.  Водинчар, М. И., Лайкова, Г. А., Рябова, Ю. К. Решение задач на смеси, растворы и сплавы методом уравнений. Математика в школе.—2001. №4.
- базисного  учебного плана на 2014- 2015  учебный год

      Согласно базисному учебному плану  на изучения данного курса в 9 классе отводится 34 часа из расчета 1 час в неделю.

      Необходимость такого курса вызвана  несколькими причинами:

- необходимостью формирования умений решения задач   различных типов ,

-  развитие логического мышления учащихся, их алгоритмической культуры и математической интуиции

- способствовать интеллектуальному развитию учащихся, формированию качеств мышления, характерных для математической деятельности и необходимых человеку для жизни в современном обществе и решения практических проблем

- подготовка  к ГИА в  9 классе

 Математика в наши дни проникает во все сферы жизни. Овладение практически любой профессией требует тех или иных знаний по математике. Особое значение в этом смысле имеет умение смоделировать математически определённые реальные ситуации. Применение на практике различных  задач, связанных с окружающей нас жизнью,  позволяет создавать такие учебные ситуации, которые требуют от учащегося умения смоделировать математически  определённые физические, химические, экономические процессы и явления, составить план действия (алгоритм) в решении реальной проблемы. Кроме того, практика последних лет говорит о необходимости формирования умений решения задач   различных типов ещё и в связи с включением их в содержание ГИА. Значительная часть учащихся испытывает серьёзные затруднения при решении текстовых задач.  В большей степени это связано с недостаточной сформированностью у учащихся умения составлять план действий, алгоритм решения конкретной задачи, культурой моделирования явлений и процессов. Большинство учащихся решают такие задачи лишь на репродуктивном уровне. Задачи же на концентрацию практически не рассматриваются в школьном курсе математики, хотя включены в содержание ГИА.

 Сначала и до конца обучения в школе математическая задача неизменно помогает ученику вырабатывать правильные математические понятия, глубже выяснять различные стороны взаимосвязей в окружающей его жизни, дает возможность применять изучаемые теоретические положения. В тоже время решение задач способствует развитию логического мышления.

Предлагаемый элективный курс «Математика вокруг нас   демонстрирует учащимся применение математического аппарата к решению повседневных бытовых проблем каждого человека, вопросов рыночной экономики и задач технологии производства. Данный элективный курс ориентирует учащихся  на обучение по естественно-научному, социально-экономическому и техническому профилю. Познавательный материал курса будет способствовать формированию устойчивого интереса учащихся к процессу и содержанию деятельности, а также познавательной и социальной активности.

     Тема «Проценты» на первом этапе основной школы, когда учащиеся в силу возрастных особенностей еще не могут получить полноценные представления о процентах, об их роли в повседневной жизни. На последующих этапах обучения повторного обращения к этой теме не предусматривается. Во многих школьных учебниках можно встретить задачи на проценты, однако в них отсутствует компактное и четкое изложение соответствующей теории вопроса. Текстовые задачи включены в материалы итоговой аттестации за курс основной школы, в КИМы и ЕГЭ, в конкурсные экзамены. Однако практика показывает, что задачи на проценты вызывают затруднения у обучающихся и очень многие окончившие школу не имеют прочных навыков обращения с процентами в повседневной жизни. Понимание процентов и умение производить процентные расчеты в настоящее время необходимы каждому человеку: Прикладное значение этой темы очень велико и затрагивает финансовую, демографическую, экологическую, социологическую и другие стороны нашей жизни.

Преподавание элективного курса   строится как углубленное  изучение вопросов, предусмотренных программой основного курса. Углубление реализуется на базе обучения методам и приемам решения математических задач, требующих применения высокой  логической культуры, развивающих  научно-теоретическое и алгоритмическое мышление .В процессе  работы возможно перераспределение часов в зависимости  от уровня подготовки учащихся.

В силу большой практической значимости данный курс вызывает интерес, является средством обучения и средством развития интеллектуальных качеств личности обучающихся. Для обучающихся, которые пока не проявляют заметной склонности к математике, эти занятии могут стать толчком в развитии интереса к предмету и вызвать желание узнать больше. Хотя при изучении курса не ставится цель выработки каких-либо специальных умений и навыков, при достаточно полном рассмотрении вопросов курса несомненно появится прогресс в подготовке обучающихся

Целями данного  элективного курса являются:

 - сформировать понимание необходимости знаний процентных вычислений для решения большого круга задач, показать широту применения процентных расчетов в реальной жизни;

— способствовать интеллектуальному развитию учащихся, формированию качеств мышления, характерных для математической деятельности и необходимых человеку для жизни в современном обществе, для общей  социальной ориентации и решения практических проблем.

- формирование умения моделировать реальные ситуации.
 -развитие исследовательской и познавательной деятельности учащихся
  -способствовать интеллектуальному развитию учащихся, формированию качеств мышления, характерных для математической деятельности и необходимых человеку для жизни в современном обществе и решения практических проблем.

 

 

 

 

 

 

 

 

                              ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ ОБУЧАЮЩИХСЯ

    В результате изучения курса учащиеся должны:
1. Знать основные способы решения задач на составление уравнений.
2. Знать основные способы моделирования реальных ситуаций при решении задач различных типов.
3. Решать задачи разного уровня (включая творческие задания) на составление уравнений.
4. Моделировать реальные ситуации, описываемые в задача.

5. Знать широту применения процентных вычислений в жизни, решать основные задачи на проценты, применять формулу сложных процентов.
6. Производить прикидку и оценку результатов вычислений.

7. При вычислениях сочетать устные и письменные приемы, применять калькулятор, использовать приемы, рационализирующие вычисления.

 

ЛИТЕРАТУРА

 

1. Н.Я. Виленкин, А.Н.Виленкин, Г.С.Сурвилло и др. Алгебра: Учебное пособие для учащихся 9 кл. с углубленным изучением математики. Под ред. Н.Я.Виленкина.я газета «Математика», приложение к «1 сентября»,2004г. №17,№23,№36, 2005 г. №2,№15,2001г.

2. Кузнецова Л.В. и др. Сборник заданий для проведения письменного экзамена по алгебре за курс основной школы. - М.: Дрофа, 2002.
3. Кузнецова Л.В.  Суворова С.Б.  Сборник заданий для подготовки итоговой аттестации в 9 классе.   - М.:  Просвещение 2007.
4.  Барабанов, О. О. Задачи на проценты как проблемы словоупотребления. Математика в школе. —2003.
5.  Башарин, Г. П. Начала финансовой математики. — М., 1997.
6.  Башарин, Г. П. Элементы финансовой математики. — М.: Математика (приложение к газете «Первое сентября»).№27— 1995.
7. Вигдорчик, Е., Нежданова, Т. Элементарная математика в экономике и бизнесе. — М., 1997.
8.  Водинчар, М. И., Лайкова, Г. А., Рябова, Ю. К. Решение задач на смеси, растворы и сплавы методом уравнений. Математика в школе.—2001. №4.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

КАЛЕНДАРНО - ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ

 

№ урока	Дата проведения урока	Наименование разделов и тем уроков	Количество часов
		Задачи на движение	4
1		Составные части задач. Структура и сущность решения задач
2		Задачи на движение двух тел
3		Задачи на движение двух тел по окружности
4		Задачи на движение двух тел по реке
		Задачи на   работу	3
5		Задачи на   работу
6		Задачи на   работу
7		Задачи на   работу
		Проценты	8
8		Проценты. Основные задачи на проценты
9		Проценты. Основные задачи на проценты
10		Сложные проценты
11		Сложные проценты
12		Сложные проценты
13		Процентные вычисления в жизненных ситуациях.
14		Процентные вычисления в жизненных ситуациях
15		Процентные вычисления в жизненных ситуациях
		Задачи на сплавы, смеси, растворы	3
16		Задачи на сплавы, смеси, растворы
17		Задачи на сплавы, смеси, растворы
18		Задачи на сплавы, смеси, растворы
		Задачи на проценты, встречающиеся на ГИА	3
19		Задачи на проценты, встречающиеся на ГИА
20		Задачи на проценты, встречающиеся на ГИА
21		Задачи на проценты, встречающиеся на ГИА
		Задачи с литературными сюжетами	3
22		Задачи с литературными сюжетами
23		Задачи с литературными сюжетами
24		Деловая игра «Проценты в современной жизни»
		Комбинированные задачи	2
25		Комбинированные задачи
26		Комбинированные задачи
		Задачи решаемые  при помощи неравенств	2
27		Задачи решаемые  при помощи неравенств
28		Задачи решаемые  при помощи неравенств
		Задачи  на нахождение оптимального решения	3
29		Задачи  на нахождение оптимального решения
30		Задачи  на нахождение оптимального решения
З1		Задачи  на нахождение оптимального решения
		Решение нестандартных задач	2
32		Решение нестандартных задач
33		Решение нестандартных задач
34		Решение задач по всему курсу	1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

СОДЕРЖАНИЕ ИЗУЧАЕМОГО КУРСА

 

 1. Составные части задач. Структура и сущность решения задач.1 час

Типы задач. Методы и способы решения задач. Основные способы моделирования задач. Составления плана решения задач.

2. Задачи на движение двух тел. (3 часа)

Обобщить и систематизировать знания учащихся по теме «Движение двух тел».

Равномерное движение. Одновременные события. Задачи на движение по реке, суше, воздуху. Задачи на определение средней скорости движения.

задач,

 

 3. Задачи на   работу.(3часа)

Обобщить и систематизировать знания учащихся по темам: работа, производительность.

 

 4. Задачи на проценты(8 часов)

. Сообщается история появления процентов; устраняются пробелы в знаниях по решению основных задач на проценты: а) нахождение процента от числа (величины); б) нахождение числа по его проценту; в) нахождение процента одного числа от другого. Актуализируются знания об арифметических и алгебраических приемах решения задач. работа. Процентные вычисления в жизненных ситуациях. Банковские операции. Основная формула процентов. Простые и сложные проценты. Средний процент изменения величины. Показ широты применения в жизни процентных расчетов. Введение базовых понятий экономики: процент прибыли, стоимость товара, заработная плата, бюджетный дефицит и профицит, изменение тарифов, пеня и др. Решение задач, связанных с банковскими расчетами: вычисление ставок процентов в банках; процентный прирост; определение начальных вкладов. Выполнение тренировочных упражнений.

5. Задачи на смеси, сплавы, растворы.(3 часа)

 

Концентрация вещества. Процентное содержание вещества. Количество вещества..
Усвоение учащимися понятий концентрации вещества, процентного раствора. Формирование умения работать с законом сохранения массы. Обобщение полученных знаний при решении задач на проценты.

6 Задачи на проценты, встречающиеся на ГИА (3 часа)

 

 7..  Задачи с литературными сюжетами. (3 часа)

Различные истории, связанные с процентными вычислениями, встречаются в ряде художественных произведений, в исторических документах и преданиях.

 Игра позволит ориентировать обучающихся на прикладное применение математических знаний в профессиональной деятельности, в неформальной обстановке произвести диагностику качества знаний учащихся по данной теме, создать условия, в которых обучающиеся могут испытать себя как будущего профессионала, проявить свои деловые качества: умение «презентовать» себя на рынке труда, умение руководить коллективом, инициативность, выносливость, смелость.

 

8. Комбинированные задачи(2часа)

 Различные способы решения комбинированных задач. Задачи,  решаемые с помощью уравнений и систем уравнений.

 

9. Задачи решаемые  при помощи неравенств. (2часа)

 

10.Задачи на нахождение оптимального решения 3часа

 

11.Решение нестандартных задач(3часа

 

 

 

ПРОЦЕНТНЫЕ ВЫЧИСЛЕНИЯ В ЖИЗНЕННЫХ СИТУАЦИЯХ
Цели: познакомить обучающихся с понятиями «скидка», «распродажа», «бюджет», «тарифы», «пеня»; сформировать умение применять знания процентов в жизненных ситуациях; закрепить умение решать основные задачи на проценты.
Занятие
РАСПРОДАЖА, ТАРИФЫ, ШТРАФЫ ( с презентацией)
Цел и: добиться усвоения учащимися таких понятий, как скидка, распродажа, тарифы, штрафы, бюджет; отработать навыки решения основных задач на проценты. (Слайд 2)
Ход занятия
1. Беседа.
Полезно подчеркнуть, что сюжеты задач взяты из реальной жизни — из газеты, объявлений, документов и т. д.
II. Закрепление. Решение задач.
1. Задача 1. (Распродажа.)  (Слайд 3)
Зонт стоил 360 р. В ноябре цена зонта была снижена на 15%, а в декабре еще на 10 %. Какой стала стоимость зонта в декабре?

Решение. (Слайд 4)
Стоимость зонта в ноябре составляла 85 % от 360 р., т. е.360•0,85 = 306(р.). Второе снижение цены происходило по отношению к новой цене зонта; теперь следует искать 90 % от 306 р., т. е. 306•0,9 = 275,4 (р.).
Ответ: 275 р. 40 к.
Дополнительный  вопрос: На сколько процентов по отношению к первоначальной цене подешевел зонт? (Слайд 5)
Решение. (Слайд 6)
Найдем отношение последней цены к исходной и выразим его в процентах. Получим 76,5 %. Значит, зонт подешевел на 23,5 %.
Ответ: 23,5%.
2. Задача 2. (Бюджет. Зарплата.) (Слайд 7)
При приеме на работу директор предприятия предлагает зарплату 4200 р. Какую сумму получит рабочий после удержания налога на доходы физических лиц?
Решение. (Слайд 8)
1) (4200 —400) 0,13 = 494 р. — налог.
2) 4200 —494 = 3706 р.
Замечание. При начислении налога на доходы физических лиц нужно учитывать стандартный вычет 400 р., налог 13 % берется от оставшейся суммы.
Ответ: 3706р.
3. Задача 3. (Слайд 9)
Заработок рабочего повысился на 20 %, а цены на продукты и другие товары снизились на 15 %. На сколько процентов рабочий теперь на свой заработок может купить больше продуктов и товаров, чем прежде?
Решен и е. (Слайд 10)
Примем для простоты вычислений прежний заработок рабочего за 10 р. и пусть он покупает только один какой-то продукт по 1 р. за килограмм, т. е. 10 кг. После повышения на 20 % заработок рабочего стал 12 р., а цена продукта после снижения цены на 15 %- 0,85 р. за 1 кг. Теперь рабочий может купить 12 : 0,85 =14,1 (кг), т. е. на 4,1 : 10 = 0,41, т. е. на 41 % больше, чем прежде.
Ответ: на  4I %больше.

4. Задача 4. (Тарифы.) (Слайд 11)
В газете сообщается, что с 10 июня согласно новым тарифам стоимость отправления почтовой открытки составит З р. 15 к. вместо 2 р. 27 к. Соответствует ли рост цен на услуги почтовой связи росту цен на товары в этом году, который составляет 14,5 %.
Решение. (Слайд 12)
Разность тарифов составляет 0,4 р., а ее отношение к старому тарифу равно 0,14545... Выразив это отношение в процентах, получим примерно 14,5 %.
Ответ: да, соответствует.
Дополнительный вопрос. Сколько будет стоить отправка заказного письма, если эта услуга сейчас оценивается в 5 р. 50 к? (Слайд 13)
Решение.
Цена услуги увеличивается на 14,5 %, т. е. станет 5,5•1,145 = 6,3 (р.).

Ответ: 6 р. 30 к.

5. Задача 5. (Штрафы.) (Слайд 14)
Занятия ребенка в музыкальной школе родители оплачивают в сбербанке, внося ежемесячно 250 р. Оплата должна производиться до 15 числа каждого месяца, после чего за каждый просроченный день начисляется пеня в размере 4 % от суммы оплаты занятий за один месяц. Сколько придется заплатить родителям, если они просрочат оплату на неделю?
Решение. (Слайд 15)
Так как 4 % от 250 р. составляют 10 р., то за каждый просроченный день сумма оплаты будет увеличиваться на 10 р. Если родители просрочат оплату на день, то им придется заплатить
250 + 10 = 260 (р.),
на неделю 250 + 107 = 320 (р.).
Ответ: 320 р.
Домашнее задание. Составить 2 задачи, используя жизненные ситуации, записать на отдельных листах.  (Слайд 16)

 

Занятие  «Задачи на сплавы, смеси, растворы» (с презентацией)

 

Ц е л и: сформировать умение работать с законом сохранения массы; обеспечить усвоение обучающимися понятий концентрации вещества, процентного раствора; обобщить полученные знания при решении задач на проценты.
Форма занятия: комбинированное занятие.
Методы обучения: рассказ, объяснение, практическая работа.
Формы контроля: проверка самостоятельно решенных задач.

Оборудование: компьютер, проектор

Ход занятия

1. Проверка домашнего задания.

II. Рассказ учителя.
Данный тип задач охватывает большой круг ситуаций — смещение товаров разной цены, жидкостей с различным содержанием соли, кислот различной концентрации, сплавление металлов с различным содержанием некоторого металла и пр. Связь различных задач между собою станет яснее, если рассматривать типичные ситуации в общем виде. При решении задач данного типа используются следующие допущения: (Слайд3)
1. Всегда выполняется «Закон сохранения объема или массы»:
если два раствора (сплава) соединяют в «новый» раствор (сплав), выполняются равенства:
V = V₁ + V₂ — сохраняется объем;
m= m₁ + m₂ — закон сохранения массы.
2. Данный закон выполняется и для отдельных составляющих частей (компонентов) сплава (раствора).
З. При соединении растворов и сплавов не учитываются химические взаимодействия их отдельных компонентов.
Задачи на смеси, растворы и сплавы называют еще задачами на процентное содержание или концентрацию. Введем основные понятия. (Слайд4) 

     Говоря о смесях, растворах и сплавах, будем употреблять термин «смесь» независимо от ее вида (твердая, жидкая, газообразная сыпучая и т. д.). Смесь состоит из «чистого вещества» и «примеси». долей а чистого вещества в смеси называется отношение количества чистого вещества т в смеси к общему количеству М смеси при условии, что они измерены одной и той же единицей массы или объема: а = т/М. Отсюда получаем т = аМ, М = т/а. Понятие доли чистого вещества можно вводить следующей условной записью.
Доля чистого вещества в смеси равна количеству чистого вещества в смеси, деленному на общее количество смеси. Заметим, что складывать и вычитать доли и процентные содержания нельзя.
Процентным содержанием чистого вещества в смеси с называют его долю, выраженную процентным отношением: с = а 100 %, а=с/ 100%.
Формула, по которой рассчитывают концентрацию смесей (сплавов):п =m_{b /}m_p, где n — концентрация, m_b — масса вещества в растворе (сплаве), m_p — масса всего раствора (сплава).

III. Решение задач.

Задача 1. (Слайд 5)

Сколько граммов воды надо добавить к 50 г раствора, содержащего 8 % соли, чтобы получить 5 % раствор?
Решение. (Слайд 6)
Пусть Х -количество воды, которое надо добавить. Новое количество раствора - (50 + Х) г. Количество соли в исходном растворе 50 •0,08 г. Количество соли в новом растворе составляет 5 % от (50 + Х) г, т. е. 0,05(50 + Х) г.
Так как количество соли от добавления воды не изменилось, то оно одинаково в исходном и новом растворах. Получаем уравнение. Иногда в химии это уравнение называют кратко «баланс по соли».
50•0,08 = 0,05(50 + Х),
50•8 = 5(50 +Х),
80 = 50 +Х,

 Х=30

Ответ: 30 г.

Задача 2. (Слайд 7)
Сколько граммов 30 %-го раствора надо добавить к 80 г 12 %-го
раствора этой же соли, чтобы получить 20 %-й раствор соли?
Решение. (Слайд 8)
Пусть надо добавить Х г 30 % раствора соли. Получится (80 + Х) г
20 % раствора. В 80 г 12 % раствора содержится 80•0,12 г соли 0,ЗХг
соли — в Х г 30 % раствора, 0,2(80 + Х) г соли — в (80 + Х) г 20 % раствора.
Получаем уравнение:
0,Зх + 0,12•80 = 0,2(80 + Х) — это и есть «баланс по соли».
0,ЗХ+9,6 =16+0,2Х,
0,ЗХ—0,2Х= 16—9,6,
0,IХ = 6,4,
Х=64.
Ответ: 64 г.
Задача 3. (Слайд 9)
Если смешать 8 кг и 2 кг растворов серной кислоты разной
концентрации, то получим 12 %-й раствор кислоты. При смешивании
двух одинаковых масс тех же растворов получим 15 %-й раствор.
Определите первоначальную концентрацию каждого раствора.
Решение. (Слайд10)

Пусть концентрация серной кислоты  в первом растворе Х%, а во втором
растворе —У%. Это значит, что в 1 кг первого раствора содержится Х/100 кг кислоты и 1-Х/100 кг воды, тогда в 8 кг первого раствора 8Х /100 кг кислоты и (8-8Х/100)кг воды.
Во втором растворе аналогично: У/100кг кислоты; (1-У/100) кг воды, в 2кг- 2У/100кг кислоты и (2- 2У/100) кг воды.
После смешения получим раствор общей массой 10 кг, в нем  содержится  (8Х/100+2У/100)  кг кислоты. По условию получаем раствор

12 %-и концентрации, значит, в 10 кг раствора будет 10• 12/100кг кислоты
Получаем уравнение  8Х/100+2У/100=1,2.
 Преобразуя, получим 4х + у = 60 — первое уравнение системы.
Рассмотрим вторую ситуацию. Пусть возьмем по 1 кг каждого
раствора, тогда будет Х/100 кг кислоты, а в 1 кг второго раствора содержится У/100кг кислоты. Так как смесь получится 15 %-й концентрации, то в (1 + 1) кг смеси должно содержаться 2*15/100 =0,3 кг кислоты.
Получаем второе уравнение   Х/100+У/100=0,3, после преобразований имеем Х+ У= 30.
Решив систему уравнений, получим Х=10, У=20.
Ответ: 10 %-й и. 20 %й растворы.

Задача 4. (Слайд 11)
Имеется два куска сплава олова и свинца, содержащие 60 % и 40% олова. По сколько граммов от каждого куска надо взять, чтобы получить 600 г сплава, содержащего 45 % олова?
Решение. (Слайд 12)
Пусть масса куска, взятого от первого сплава т₁ г, тогда масса куска от второго сплава будет 600 - т₁, составим уравнение
т₁•0,6 +(б00— т₁)•0,4= 600•0,45,
6 т₁₊2400—4 т₁ =2700,
20 т₁ = 3000,

т₁ = 150,
600— т₁ =450,
т₂=450.
Ответ: I50г;450г.

Домашнее задание: Даны два куска с различным содержанием олова. Первый, массой 300 г, содержит 20 % олова. Второй, массой 200 г, содержит 40 % олова. Сколько процентов олова будет содержать сплав, полученный из этих кусков. (Слайд 13)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Примерный дидактический материал для занятий.

 

Тема 1. Составные части задач. Структура и сущность    решения задач.

 Типы задач:

1.                                                               Изменение величины и сравнение её значений.

2.                                                               Задачи на работу.

3.                                                               Задачи на движение двух тел.

4.                                                               Задачи на смеси и сплавы.

Блок-схема алгоритма решения задач.

 

Тема 2. Задачи на движение двух тел.

 

 Задача 1. (Средняя скорость движения)

Средней скоростью движения на некотором участке пути называют постоянную скорость, с которой можно тот же участок пути пройти за то же время.

 

Турист шёл со скоростью А км/ч , а точно такое же время со скоростью В км/ч. Какова средняя скорость движения туриста на всём участке пути?

Решение:

Пусть турист  шёл  Х км со скоростью Акм/ч и столько же Х ч– со скоростью В км/ч.Тогда за 2Х ч он прошёл АХ+ВХ=Х(А+В) км. Средняя скорость туриста равна:

 км/ч.

Задача 2.

Автомобиль ехал из А в В порожняком со скоростью 60 км/ч, а возвращался   с грузом  со скоростью 40 км/ч.Найдите среднюю скорость движения на всём участке движения.

Задача 3.

В гору велосипедист ехал со скоростью 10 км/ч, а с горы с некоторой другой скоростью. Как он подсчитал, средняя скорость движения была12 км/ч . С какой скоростью он ехал с горы?

Решение в общем виде:

       Х=

 Задачи на "Движение по реке"

Сформулируем задачу в общем виде:

Лодка от А до В плывёт по течению t часов, а от В до А(против течения) k часов. Сколько часов будет плыть бревно от А до В?

Задача 4.

Я грёб вверх по течению и, проплывая под мостом, потерял шляпу. Через 10 мин. Я это заметил и, повернув и гребя с той же силой, нагнал шляпу в 1 км ниже моста. Какова скорость течения?

Тема 3. Задачи на   работу.

При решении задач на работу нередко в условии задачи говорится о выполнении некоторого задания без указания конкретных единиц, в которых измеряется работа. В этом случае обычно принимают всю работу за единицу: А=1. Как правило, для составления уравнения или системы уравнений, буквами обозначаются в первую очередь производительности участников работы, а остальные величины вводятся по мере необходимости.
 Задача 5.

Два экскаватора разной мощности, работая совместно, выполняют работу за 6 часов. Если первый проработает 4 часа, а затем второй 6 часов, то они выполнят 80% всей работы. За какое время каждый экскаватор отдельно может выполнить всю работу?

Решение:

Пусть Х-производительность первого экскаватора, а У- производительность второго экскаватора. Вся работа-1.

Так как экскаваторы работают совместно 6ч с производительностью Х+У и выполняют всю работу, то составим уравнение: (Х+У)6=1.

Первый экскаватор работает 4ч с производительностью Х., а затем 6ч второй экскаватор с производительностью У, и выполняют 0,8 всей работы, то 4Х+6У=0,8. Решим систему уравнений:

 

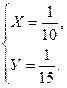
Поскольку время, необходимое для выполнения всей работы, и производительность связаны соотношением t=t=, то t=10ч, t=15ч.

Ответ: 10ч, 15ч.

Задача 6.

Два каменщика, второй из которых начинает работать позже первого на 3 дня, могут  выстроить стену за 14 дней. Первому  каменщику потребовалось бы на выполнение этой работы на 6 дней больше, чем второму. За сколько дней может выстроить эту стену каждый каменщик в отдельности?

Задача 7.

Для разгрузки баржи имеется три крана. Первому крану для разгрузки всей баржи требуется времени в четыре раза меньше, чем второму, и на 9 часов больше, чем третьему. Три крана, работая вместе, разгрузили бы баржу за 18 часов, но по условиям эксплуатации одновременно могут работать только два крана. Определите наименьшее время (в часах) необходимое для разгрузки баржи.(Производительность каждого крана постоянна в течении всей работы)

Ответ: 20ч.

Тема  4.Задачи на проценты.

 1. Процент – сотая часть числа.

2. Чтобы найти р% от всего числа, надо всё число умножить на 0.01р.

3. Чтобы найти всё число по его р% процентам, надо известное число разделить на   0.01р.

4. Чтобы найти сколько процентов одно число составляет от другого, надо одно число разделить на другое и умножить на 100%.

Задача 8.

Сколько процентов соли содержится в растворе, если в 200г. раствора содержится 150г. воды?

Решение:

1)                                                              200-150=50(г.) – соли

2)                                                              50*100%=25% - соли

           200

Ответ: 25%

Задача 9.

Кофе при жарке теряет 12% своей массы. Сколько свежего кофе надо взять, чтобы получить 14.08 кг. жареного кофе?

Задача 10.

На сколько процентов увеличится произведение двух чисел, если одно из них увеличить на 30%, а другое - на 20 %?

Задача 11.

Свежие грибы содержали по массе 90% воды, а сухие 12%. Сколько получится сухих грибов из 22 кг свежих?

Решение:
1) 22 ^. 0,1 = 2,2 (кг) - грибов по массе в свежих грибах;
2) 2,2 : 0,88 = 2,5 (кг) - сухих грибов, получаемых из свежих.
         Ответ: 2,5 кг.

Задача 12.(из ЕГЭ).

Цену товара повышали: первый раз на р%, затем новую цену повысили на 2р%. После этого цену товара снизили на 15%. В итоге окончательная цена оказалась выше первоначальной на 12.2%. На сколько процентов была повышена цена товара в первый раз?

Простые проценты.

  Обозначим через А сумму первоначального вклада. Банк  обязуется выплачивать вкладчику в конце каждого p% (годовая процентная ставка) от первоначальной суммы А. По истечении одного года величина вклада станет равной А= А(1+) рублей.  Если по прошествии каждого года вкладчик снимает со счёта начисленные проценты, то через n лет на вкладе по формуле простого процента будет:

 А= А(1+) .

  Задача 13. 

Банк выплачивает вкладчикам каждый год 8% от внесённой суммы. Клиент сделал вклад в размере 200000р.Какая сумма будет на его счёте через 5 лет, 10 лет?

Решение:
Используя формулу : А= А(1+)

А=200000(1+)=280000 (р)

 

 А=200000(1+)=360000 (р)

         Ответ: 280000 р., 360000 р.

  Задача  14.

При какой процентной ставке вклад на сумму 500р. Возрастёт за 6 месяцев до 650 р.

Ответ: 5%.

Задача  15.

 Каким должен быть начальный вклад, чтобы при ставке 4% в месяц он увеличился за 8 месяцев до 33000р.

Ответ:  25000р.

  Сложные проценты

Если обозначить через А сумму первоначального вклада, А- сумма, которая будет на вкладе к концу n-го года, то при начислении p% годовых, не снимая со счёта сумму начисленных процентов, можно пользоваться формулой сложных процентов:

А= А .

 Задача  16.

Банк предлагает вклад «студенческий». По этому вкладу сумма, имеющаяся  на 1 января, ежегодно увеличивается на одно и то же число процентов. Вкладчик вложил 1 января 1000 рублей и в течение 2 лет не производил со своим вкладом никаких операций. В результате вложенная им сумма увеличилась до 1210 рублей. На сколько процентов ежегодно увеличивается сумма денег, положенная на этот вклад?

Решение:

Пусть на a%  ежегодно увеличивается сумма денег, положенная на «студенческий» вклад. Так как было положено 1000 рублей, а к концу второго года получилось 1210 рублей, то А=1000;  А=1210; n=2.

Решим уравнение :

1210=1000.

а= 10.

Ответ : 10%.

Задача 17.

Рассчитайте, что выгоднее для вкладчика: получить 20 000 рублей сегодня или получить 35 000 рублей через 3 года, если процентная ставка равна 17%.

Рассчитаем будущую стоимость 20000 рублей через 3 года, под 17% годовых.
  А= 20000 * (1 + 0,17)³ = 32032 рубля.

Ответ. Получить 35000 рублей через 3 года является более выгодным решением, при данном значении процентной ставки.

Задача 18.

Какой должна быть ставка ссудного процента, чтобы 10000 рублей нарастились до30000 рублей, за срок вклада 5 лет?                                                                                               Ответ. 10 000 рублей нарастятся до 30 000 рублей за 5 лет при ставке ссудного процента 24,573%

Тема 5. Задачи на смеси, сплавы и растворы.

Смесь состоит из «чистого вещества» и «примеси».Долей а чистого вещества в смеси называется отношение количества чистого вещества m в смеси к общему количеству М смеси при условии, что они измерены одной и той же единицей массы или объёма: а=m/М.

Процентным содержанием чистого вещества в смеси с называют его долю, выраженную процентным отношением: с=а 100%.

Задача 19.

В 2 литра 10% раствора уксусной кислоты добавили 8 литров чистой воды. Определить процентное содержание уксусной кислоты в полученном растворе.

Решение:

2л – 100%

Воды – 1,8л.

Кислота – 0,2л.

После добавления воды стало 9,8л. Воды, поэтому процентное содержание

(0,2\(0,2+9,8))*100%=2%

Ответ: 2%.

Задача 20.

 Сплав содержит 10 кг олова и 15 кг цинка. Каково процентное содержание олова и цинка в сплаве?
Решение:

Процентное содержание вещества в сплаве - это часть, которую составляет вес данного вещества от веса всего сплава.

1) 10 + 15 = 25 (кг) - сплав;
2) 10/25 ^. 100% = 40% - процентное содержание олова в сплаве;
3) 15/25 ^. 100% = 60% - процентное содержание цинка в сплаве;
          Ответ: 40%, 60%.

 Задача 21.

Сплав олова с медью весом 12кг. Содержит 45% меди. Сколько чистого олова нужно добавить, чтобы получить сплав, содержащий 40% меди.

Задача 22.

 Имеется 2 сплава, в одном из которых содержится 40%, а в другом 20% серебра. Сколько кг второго сплава нужно добавить к 20 кг первого, чтобы после сплавления вместе получить сплав, содержащий 32% серебра?

 Задача 23.

 К 15 л 10%-ного раствора соли добавили 5%-ный раствор соли и получили 8%-ный раствор. Какое количество литров 5%-ного раствора добавили?

Задачи на концентрацию.

Формула концентрации    смеси (сплава) :

n=,

n – концентрация,

m- масса вещества в растворе (сплаве),

m- масса  всего раствора.

 

 Если концентрация вещества в соединении по массе составляет р%, то это означает, что масса этого вещества составляет р% от массы всего соединения.

Отношения объема чистой компоненты в растворе ко всему объему смеси называется объемной концентрацией этой компоненты.

Сумма концентраций всех компонент, составляющих смесь, равна 1. В этом случае концентрация - безразмерная величина.

Если известно процентное содержание вещества, то его концентрация находится по формуле:                   n=

n - концентрация вещества;
р - процентное содержание вещества (в процентах).

Задача 24.

К 20кг. 12%-раствора соли добавили 3кг. соли. Сколько надо долить воды, чтобы концентрация соли в растворе не изменилась.

1) 0.12*20=2.4(кг.) – масса соли в первоначальном растворе

2) 2.4+3=5.4(кг.) – масса соли в полученном растворе

Пусть Х(л.) воды требуется долить.

Запишем пропорцию:

20+Х=5.4

   20    2.4

2.4(20+Х)=5.4*20

48+2.4х=108

2.4х=60

х=25(кг.)

Ответ: 25(кг.)

Задача 25.

Если смешать 8 кг и 2кг растворов серной кислоты разное концентрации, то получим 12% раствор кислоты. При смешивании двух одинаковых масс тех же растворов получим 15% раствор. Определите первоначальную концентрацию каждого раствора.

Ответ: 10%-й и 20%-й растворы.

Задача 26.

Сколько граммов надо добавить к 100г. 30-% соляной кислоты, чтобы получить 10%-кислоту?

Задача 27.

 К раствору, содержащему 39г. соли, добавили 1л. воды, после чего концентрация соли уменьшилась на 10%. Найти первоначальную концентрацию соли в растворе.

Задача 28.

В колбе было 800г 80% спирта. Провизор отлил из колбы 200г этого спирта и добавил в неё 200г воды. Определите концентрацию ( в %) полученного спирта.

 Тема 6. Комбинированные задачи.

Задачи,  решаемые с помощью уравнений.  

Задача 29.

Магазин в первый день продал половину привезённых гусей да ещё  гуся; во второй день  часть остатка да ещё  гуся, а в третий день магазин продал оставшихся 33 гусей. Сколько всего гусей было привезено в магазин?

Решение:

Пусть было привезено в магазин х гусей. Тогда магазин продал:

1)                                                              в первый день гусей;

2)                                                              во второй деньгусей;

3)                                                              в третий день 33 гуся.

Составим уравнение и решим его.

++33=х,

,

-,

х=101.

Ответ: 101 гусь.

Задача 30.

Автомобилист проехал расстояние между двумя городами за 3 дня. В первый день он проехалвсего пути и ещё 60 км, во второй он проехал всего пути и ещё20 км, а в третий день он проехал  всего пути и оставшиеся 25 км. Найдите расстояние между городами.

Ответ:400 км.

Задача 31.

В течении года завод дважды увеличивал выпуск продукции на одно и то же число процентов. Найдите это число, если известно, что в начале года завод ежемесячно выпускал 600 изделий, а в конце года стал выпускать ежемесячно 726 изделий.

Ответ:10%.

Задача 32.

Моторная лодка, скорость которой в стоячей воде равна 10 км/ч, проплыла по течению 91 км и вернулась обратно. Найдите скорость течения реки, если лодка провела в пути 20 часов.

Ответ: 3 км/ч.

Задачи, решаемые с помощью систем уравнений.

Задача 33.

Имеются два раствора серной кислоты в воде: первый – 40%-й, второй- 60%-й. Эти два раствора смешали , после чего добавили 5 кг чистой воды и получили 20% раствор. Если бы вместо 5 кг чистой воды добавили 5 кг 80%-го раствора, то получился бы 70%-й раствор. Сколько было 40%-го раствора и 60%-го раствора?

Решение:

	Масса серной Кислоты, кг	Масса раствора	Концентрация
1-й раствор	0,4х	х	40%=0.4
2-й раствор	0,6у	у	60%=0,6
Первая смесь	0,4х+0,6у	х+у+5
Вторая смесь	(0,4х+0,6у)+ +5 =0,4х+0,6у+4	х+у+5

По условию доля серной кислоты в первой смеси равна 20%=0,2, а во второй смеси равна 70%=0,7.

Составим и решим систему уравнений:

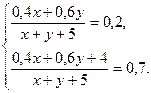
Пусть 0,4х+0,6у=а, х+у+5=b. Тогда система примет вид

     

 

   

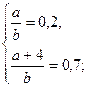
1 кг –масса 40%-го раствора серной кислоты.

2 кг- масса 60%-го раствора серной кислоты.

Ответ: 1 кг, 2 кг.

Задача

Имеется кусок сплава меди с оловом общей массой 12 кг, содержащий 45% меди. Сколько чистого олова надо прибавить к этому куску сплава, чтобы получившийся новый сплав содержал 40% меди?

Ответ: 1,5 кг.

Задача 34.

 В реку впадает приток. Катер отходит от пункта А, находящегося на притоке, плывёт по течению 80 км до впадения притока в реку в пункте В, а затем идёт вверх по реке до пункта С. На путь от А до С он затратил 18 часов, на обратный путь – 15 часов. Найдите расстояние от В до С, если известно, что скорость течения реки3км/ч, а собственная скорость катера 18 км/ч.

Ответ: 210 км.

Задача 35.

Фирма А  может выполнить заказ на производство игрушек на 4 дня быстрее, чем фирма В. За какое время может выполнить этот заказ каждая фирма, если известно, что  при совместной работе за 24 дня они выполняют заказ в 5 раз больший?

Ответ: фирма А за 8 дней, фирма В за 12 дней

Задачи, которые решают при помощи неравенств.

Задача 36.

В контейнере находятся коробки и ящики общим числом  более 16. Если вдвое увеличить количество коробок и на 20 – количество ящиков, то ящиков будет больше, чем коробок.

Решение.

Пусть х- количество коробок, а у- количество ящиков в контейнере. По смыслу задачи х и у- натуральные числа. По условию задачи составим систему неравенств:

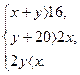
Преобразуем данную систему:

На координатной плоскости найдём множество точек (х;у), удовлетворяющих этим условиям.

 

Точки лежащие внутри ΔАВС, и будут удовлетворять данным условиям. Это одно точка с натуральными координатами-(12;5). Следовательно, количество коробок может быть только 12, при этом  ящиков должно быть 5.

Проверка: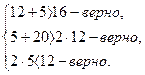

Ответ : 12 коробок.

Задача 37.

Из пункта А в пункт В, находящийся на расстоянии 105 км от пункта А, со некоторой скоростью выезжает автобус. Через 30 минут вслед за ним из А со скоростью 40 км/ч отправляется автомобиль, который догнав автобус, поворачивает обратно. Определите скорость автобуса, при которой автомобиль возвращается в А позже, чем автобус приходит в В.

Решение.

Пусть х км – расстояние от пункта А до места встречи автобуса и автомобиля. Обозначим v км/ч скорость автобуса.

Время, которое затрачивает автобус на путь из А в В, равно  ч. Время, которое затрачивает автомобиль, чтобы догнать автобус и вернуться в А, с учётом его более позднего, на 0,5 ч, отправления, составляет  ч. По условию задачи время движения автомобиля больше времени автобуса, т.е.  . По условию задачи время, затраченное автобусом на путь от А до места встречи, на 0,5 ч больше времени, которое потребовалось автомобилю, чтобы догнать автобус, т.е. ,   х= В результате неравенство примет вид:

 

,

.

как 0, 0, то умножая обе части неравенства на 2v(40-v)0, имеем:

2v+(40-v) v210(40-v),

v+250v-8400,

Учитывая условие задачи, решение неравенства имеет вид: v30.

По условию задачи встреча произошла до пункта В, т.е. 0.В результате имеем ещё одно неравенство:

0,  так как  0,то

 

0,

0.

Учитывая, что : v30 , окончательный результат:

30, при таких скоростях, автомобиль возвращается в А позже, чем автобус приходит в В.

Ответ: 30.

Задача 38.

На реке, скорость течения которой 5 км/ч, в направлении её течения расположены пристани А,В и С, причём В находится посередине между А и С. От пристани В одновременно отходят плот , который движется по течению к пристани С, и катер, который идёт к пристани А, причём скорость катера в стоячей воде равна v км/ч. Дойдя до пристани А, катер разворачивается и движется по направлению к пристани С. Найдите все те значения v, при которых катер приходит в С позже, чем плот.

Ответ: 515 км/ч.

Тема 7. Решение задач по всему курсу.

Задача 39.( производительность)

В бассейн проведена труба. Вследствие её засорения приток  воды уменьшился на 60%. На сколько процентов вследствие увеличится время, необходимое для заполнения бассейна?

Ответ: 150%

Задача 40.

Имеются 2 слитка, содержащие медь. Масса 2 слитка на 3кг. Больше, чем масса 1 слитка. Процентное содержание меди в первом слитке – 10%; во втором – 40%. После сплавливания этих двух слитков получился слиток, процентное содержание меди в котором – 30%. Определить массу полученного слитка.

Ответ: 9кг.

Задача 41.

Из турбазы в одном направлении выходят три туриста с интервалом в 30 мин. Первый идёт со скоростью 5 км/ч, второй – 4 км/ч. Третий турист догоняет первого. Найдите скорость третьего туриста.

Ответ: 6 км/ч.

Задача 42.

  За определённое время на автозаводе должны были собрать 160 автомобилей. Первые 2 ч выполнялась установленная почасовая норма, а затем стали забирать на 3 автомобиля больше. В результате за 1 ч до срока было собрано 155 автомобилей. Сколько автомобилей в час планировали собирать первоначально?

Ответ:  20автомобилей.