Элективный курс по математике (10 класс)

Пояснительная записка

Рабочая программа курса составлена на основе обучающей системы подготовки к ЕГЭ Дмитрия Гущина.

Программа данного элективного курса ориентирована на рассмотрение отдельных вопросов математики, которые входят в содержание единого государственного экзамена. Курс дополняет и развивает школьный курс математики, а также является информационной поддержкой дальнейшего образования и ориентирован на удовлетворение образовательных потребностей старших школьников, их аналитических и систематических способностей. Основная идея данного элективного курса заключена в расширении и углублении знаний обучающихся по некоторым разделам математики, в обеспечении прочного и сознательного овладения обучающимися системой математических знаний и умений, необходимых при сдаче выпускного экзамена, а для некоторых школьников – необходимых для продолжения образования.

Изучение курса предполагает обеспечение положительной мотивации обучающихся на повторение ранее изученного материала, выделение узловых вопросов курса, предназначенных для повторения, использование схем, моделей, опорных конспектов, справочников, компьютерных тестов, самостоятельное составление тестов аналогичных заданиям ЕГЭ.

Старшие школьники уже включаются в новый тип деятельности — учебно-профессиональный. Учебная деятельность для обучающихся 10 класса является средством реализации жизненных планов, поэтому она направлена на структурную организацию и систематизацию индивидуального опыта путем его расширения и пополнения. В этом возрасте учебная информация может быть осмыслена самостоятельно и ученики способны самостоятельно выбирать формы получения информации. Одной из возможных форм является данный элективный курс.

     Цель данного курса: создание условий для формирования и развития у обучающихся самоанализа и систематизации полученных знаний.

    Задачи курса:

• Расширение и углубление школьного курса математики.

• Актуализация, систематизация и обобщение знаний обучающихся по математике.

• Формирование у обучающихся понимания роли математических знаний как инструмента, позволяющего выбрать лучший вариант действий из многих возможных.

• Развитие интереса обучающихся к изучению математики.

• Расширение научного кругозора обучающихся.

• Обучение старшеклассников решению учебных и жизненных проблем, способами анализа информации, получаемой в разных формах.

• Формирование понятия о математических методах при решении сложных математических задач.

• Обучение заполнению бланков ЕГЭ.

• Психологическая подготовка к ЕГЭ.

Согласно учебному плану общеобразовательного учреждения на изучение элективного курса в 10 классе отводится 68 часов.

Курс состоит из двух модулей: «Алгебра» и «Геометрия». Темы распределены в соответствии с прохождением материала школьного курса математики 10 класса.

Выбор тем обусловлен следующими причинами:

1. Необходимостью более глубокого изучения указанных тем в соответствии с требованиями ЕГЭ.

2. Логическим соответствием данных тем программе по алгебре и геометрии 10 класса, что позволяет значительно расширить и углубить знания обучающихся.

3. Пожеланиями обучающихся.

На изучение предмета отводится 2 часа в неделю, итого 68 часов за учебный год.

Ожидаемые результаты

Изучение данного курса дает учащимся возможность:

1. Повторить и систематизировать ранее изученный материал школьного курса математики;

2. Овладеть навыками построения и анализа предполагаемого решения поставленной задачи;

3. Познакомиться и использовать на практике нестандартные методы решения задач;

4. Повысить уровень своей математической культуры, творческого развития, познавательной активности;

5. Познакомиться с возможностями использования электронных средств обучения, в том числе Интернет-ресурсов, в ходе подготовки к итоговой аттестации в форме ЕГЭ

Контроль ожидаемых результатов

Эффективность обучения отслеживается следующими формами контроля: контрольные и самостоятельные работы, тестирование.

Курс заканчивается итоговой контрольной работой.

В рамках данного элективного курса предполагается безоотметочная система оценивания.

Методы и формы обучения

В связи с учетом особенностей обучающихся в процессе обучения используются следующие формы уроков:

• лекция

• практикум

• занятие-обсуждение

• консультация

• обучение через опыт и сотрудничество;

• интерактивность (тренинги, вне занятий - метод проектов);

• личностно-деятельностный и субъект–субъективный подход (большее внимание к личности)

Содержание элективного курса

Финансовая математика

Банки. Вклады. Кредиты.

Задачи с параметром

Уравнения с параметром. Неравенства с параметром.

Системы уравнений с параметром. Системы неравенств с параметром.

Планиметрические задачи

Многоугольники и их свойства. Окружности и треугольники. Окружности и четырехугольники. Окружности и системы окружностей. Задачи на доказательство и вычисление.

Числа и их свойства

Числа и их свойства. Числовые наборы на карточках и досках. Последовательности и прогрессии. Задачи с экономическим содержанием.

Сюжетные задачи.

Неравенства

Рациональные неравенства. Иррациональные неравенства. Неравенства с модулем. Смешанные неравенства.

Уравнения

Логарифмические и показательные уравнения. Тригонометрические уравнения. Уравнения смешанного типа.

Стереометрические задачи

Угол между скрещивающимися прямыми. Угол между прямой и плоскостью.

Угол между плоскостями. Расстояние от точки до прямой и до плоскости.

Расстояние между прямыми и плоскостями.

Учебно-тематический план

Календарно-тематическое планирование

Учебно-методическое обеспечение

для учителя

1.    ЕГЭ. Математика. Профильный уровень. Самостоятельная подготовка

2.    к ЕГЭ. Универсальные материалы с методическими рекомендациями, решениями и ответами / Л.Д. Лаппо, М.А. Попов. – М.: Издательство «Экзамен», 2015. – 351, (1) с. (Серия «ЕГЭ. Полный курс»)

3.    ЕГЭ 2017. Математика. Профильный уровень. Демоверсия, спецификация, кодификатор.

4.    Математика. Подготовка к ЕГЭ 2016. Профильный уровень/Д.А. Мальцев, А.А. Мальцев, Л.И. Мальцева – Ростов н/Дону: Издатель Мальцев Д.А.; М.: Народное образование,2016. – 188, (1) с.

5.    Математика. Подготовка к ЕГЭ-2016. Профильный уровень. 40 тренировочных вариантов по демоверсии на 2016 год: учебно-методическое пособие. Под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова - Ростов-на-Дону: Издательство «Легион», 2015 . – 352 с.

6.    Подготовка к ЕГЭ по математике в 2016 году. Профильный уровень. Методические указания / И.В. Ященко, С.А. Шестаков, А.С. Трепалин. – М.: МЦНМО, 2016. – 204 с.

Интернет ресурсы

1.      http://ege.sdamgia

2.      http://mathege.ru

3.      http://uztest.ru/exam

4.      http://egeru.ru

Учебно-методическое обеспечение

для учащихся

1.    ЕГЭ – 2016 : Математика: 30 вариантов экзаменационных работ для подготовки к единому государственному экзамену: профильный уровень / под ред. И.В. Ященко. – Москва: АСТ: Астрель, 2016. – 135, (1) с. – (Государственная аттестация).

2.    ЕГЭ 2017. Математика. Профильный уровень. Типовые тестовые задания/ И.В. Ященко, М.А. Волчкевич, И.Р.Высоцкий, Р.К. Гордин, П.В.Семенов, О.Н. Косухин, Д.А. Федоровых, А.И. Суздальцев, А.Р. Рязановский, И.Н. Сергеев, В.А. Смирнов, А.В. Хачятурян, С.А. Шестаков, Д.Э. Шноль; под ред. И.В. Ященко. – М.: Издательство «Экзамен», 2017. – 55, (1) с.

3.    Математика. Подготовка к ЕГЭ 2016. Профильный уровень/Д.А. Мальцев, А.А. Мальцев, Л.И. Мальцева – Ростов н/Дону: Издатель Мальцев Д.А.; М.: Народное образование,2016. – 188, (1) с.

4.    Математика. Подготовка к ЕГЭ-2016. Профильный уровень. 40 тренировочных вариантов по демоверсии на 2016 год: учебно-методическое пособие. Под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова - Ростов-на-Дону: Издательство «Легион», 2015 . – 352 с.

Интернет ресурсы

1.     http://ege.sdamgia

2.      http://mathege.ru

3.      http://uztest.ru/exam

4.      http://egeru.ru

Приложение

Контрольная работа №1

Финансовая математика. Планиметрия

1.     В одной стра­не в об­ра­ще­нии на­хо­ди­лось 1 000 000 дол­ла­ров, 20% из ко­то­рых были фаль­ши­вы­ми. Некая кри­ми­наль­ная струк­ту­ра стала вво­зить в стра­ну по 100000 дол­ла­ров в месяц, 10% из ко­то­рых были фаль­ши­вы­ми. В это же время дру­гая струк­ту­ра стала вы­во­зить из стра­ны 50 000 дол­ла­ров еже­ме­сяч­но, из ко­то­рых 30% ока­за­лись фаль­ши­вы­ми. Через сколь­ко ме­ся­цев со­дер­жа­ние фаль­ши­вых дол­ла­ров в стра­не со­ста­вит 5%?

2.     Найдите все зна­че­ния a, при каж­дом из ко­то­рых урав­не­ние    имеет един­ствен­ный ко­рень.

3.     Най­ди­те все зна­че­ния па­ра­мет­ра a, при каж­дом из ко­то­рых не­ра­вен­ство

имеет един­ствен­ное целое ре­ше­ние.

4.     Най­ди­те все зна­че­ния a, при каж­дом из ко­то­рых си­сте­ма урав­не­ний

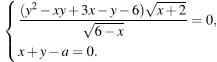имеет ровно два раз­лич­ных ре­ше­ния.

5.     Най­ди­те все зна­че­ния a, при каж­дом из ко­то­рых си­сте­ма

имеет един­ствен­ное ре­ше­ние.

Контрольная работа №2

Планиметрические задачи

1.     Пря­мая, про­ведённая через се­ре­ди­ну N сто­ро­ны AB квад­ра­та ABCD, пе­ре­се­ка­ет пря­мые CD и AD в точ­ках M и T со­от­вет­ствен­но и об­ра­зу­ет с пря­мой AB угол, тан­генс ко­то­ро­го равен 4. Най­ди­те пло­щадь тре­уголь­ни­ка BMT, если сто­ро­на квад­ра­та ABCD равна 8.

2.     Рас­сто­я­ние между па­рал­лель­ны­ми пря­мы­ми равно 4. На одной из них лежит точка C, а на дру­гой — точки A и B, при­чем тре­уголь­ник ABC — рав­но­бед­рен­ный и его бо­ко­вая сто­ро­на равна 5. Най­дите ра­ди­ус окруж­но­сти, впи­сан­ной в тре­уголь­ник ABC.

3.     Окруж­ность S ра­ди­у­са 24 впи­са­на в рав­но­бед­рен­ную тра­пе­цию с ос­но­ва­ни­я­ми 36 и 64. Най­ди­те ра­ди­ус окруж­но­сти, ко­то­рая ка­са­ет­ся ос­но­ва­ния, бо­ко­вой сто­ро­ны и окруж­но­сти S.

4.     Окруж­но­сти ра­ди­у­сов 2 и 3 с цен­тра­ми O₁ и O₂ со­от­вет­ствен­но ка­са­ют­ся в точке A. Пря­мая, про­хо­дя­щая через точку A, вто­рич­но пе­ре­се­ка­ет мень­шую окруж­ность в точке B, а боль­шую — в точке C. Най­ди­те пло­щадь тре­уголь­ни­ка BCO₂, если ∠ABO₁ = 30°.

5.     В тре­уголь­ни­ке АВС про­ве­де­на бис­сек­три­са АМ. Пря­мая, про­хо­дя­щая через       вер­ши­ну В пер­пен­ди­ку­ляр­но АМ, пе­ре­се­ка­ет сто­ро­ну АС в точке N. АВ = 6; ВС = 5; АС = 9.

а) до­ка­жи­те, что бис­сек­три­са угла С делит от­ре­зок МN по­по­лам;

б) пусть Р — точка пе­ре­се­че­ния бис­сек­трис тре­уголь­ни­ка АВС. Най­ди­те от­но­ше­ние АР : РN.

Контрольная работа №3

Числа и их свойства

1.     Наи­боль­шее целое число, не пре­вос­хо­дя­щее число x, равно

Най­ди­те все такие зна­че­ния x.

2.     На доске на­пи­са­но число 2015 и еще не­сколь­ко (не менее двух) на­ту­раль­ных чисел, не пре­вос­ходя­щих 5000. Все на­пи­сан­ные на доске числа раз­лич­ны. Сумма любых двух из на­пи­сан­ных чисел де­лит­ся на какое-ни­будь из осталь­ных.

           а) Может ли на доске быть на­пи­са­но ровно 1009 чисел?

           б) Может ли на доске быть на­пи­са­но ровно пять чисел?

           в) Какое наи­мень­шее ко­ли­че­ство чисел может быть на­пи­са­но на доске?

 3. Воз­рас­та­ю­щая ко­неч­ная ариф­ме­ти­че­ская про­грес­сия со­сто­ит из раз­лич­ных целых не­от­ри­ца­тель­ных чисел. Ма­те­ма­тик вы­чис­лил раз­ность между квад­ратом суммы всех чле­нов про­грес­сии и сум­мой их квад­ра­тов. Затем ма­те­ма­тик до­ба­вил к этой про­грес­сии сле­ду­ю­щий её член и снова вы­чис­лил такую же раз­ность.

          а) При­ве­ди­те при­мер такой про­грес­сии, если во вто­рой раз раз­ность ока­за­лась на 48 боль­ше, чем в пер­вый раз.

          б) Во вто­рой раз раз­ность ока­за­лась на 1440 боль­ше, чем в пер­вый раз. Могла ли про­грес­сия сна­ча­ла со­сто­ять из 12 чле­нов?

          в) Во вто­рой раз раз­ность ока­за­лась на 1440 боль­ше, чем в пер­вый раз. Какое наи­боль­шее ко­ли­че­ство чле­нов могло быть в про­грес­сии сна­ча­ла?

 4. В игре «Дро­ти­ки» есть 20 на­руж­ных сек­то­ров, про­ну­ме­ро­ван­ных от 1 до 20 и два цен­траль­ных       сек­то­ра. При по­па­да­нии в на­руж­ный сек­тор игрок по­лу­ча­ет ко­ли­че­ство очков, сов­па­да­ю­щее с но­ме­ром сек­то­ра, а за по­па­да­ние в цен­траль­ные сек­то­ра он по­лу­ча­ет 25 или 50 очков со­от­вет­ствен­но. В каж­дом из на­руж­ных сек­то­ров есть об­ла­сти удво­е­ния и утро­е­ния, ко­то­рые, со­от­вет­ствен­но, удва­и­ва­ют или утра­и­ва­ют но­ми­нал сек­то­ра. Так, на­при­мер, по­па­да­ние в сек­тор 10 (не в зоны удво­е­ния и утро­е­ния) дает 10 очков, в зону удво­е­ния сек­то­ра ― 20 очков, в зону утро­е­ния ― 30 очков.

           а) Может ли игрок тремя брос­ка­ми на­брать ровно 167 очков?

           б) Может ли игрок ше­стью брос­ка­ми на­брать ровно 356 очков?

           в) С по­мо­щью ка­ко­го наи­мень­ше­го ко­ли­че­ства брос­ков, игрок может на­брать ровно 1001 очко?

Контрольная работа №4

Уравнения и неравенства

1.     Ре­ши­те не­ра­вен­ство:

2.     Решить неравенство:

3.     Ре­ши­те не­ра­вен­ство:  

4.     Ре­ши­те урав­не­ние

Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие от­рез­ку

5.     а) Ре­ши­те урав­не­ние:

б) Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие от­рез­ку .

Контрольная работа №5

Стереометрические задачи

1.     Длина ребра пра­виль­но­го тет­ра­эд­ра ABCD равна 1. Най­ди­те угол между пря­мы­ми DM и CL, где M — се­ре­ди­на ребра BC, L — се­ре­ди­на ребра AB.

2.     В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­де ABCDA₁B₁C₁D₁, у ко­то­ро­го AA₁ = 4, A₁D₁ = 6, C₁D₁ = 6, най­ди­те тан­генс угла между плос­ко­стью ADD₁ и пря­мой EF, про­хо­дя­щей через се­ре­ди­ны ребер AB и B₁C₁.

3.      В пра­виль­ной че­ты­рех­уголь­ной пи­ра­ми­де PABCD, все ребра ко­то­рой равны 6, точка K ― се­ре­ди­на бо­ко­во­го ребра AP.

          а) По­строй­те се­че­ние пи­ра­ми­ды плос­ко­стью, про­хо­дя­щей через точку K и па­рал­лель­ной плос­ко­сти BCP.

          б) Най­ди­те угол между плос­ко­стью се­че­ния и плос­ко­стью ос­но­ва­ния пи­ра­ми­ды.

4. В кубе ABCDA₁B₁C₁D₁ все ребра равны 1. Най­ди­те рас­сто­я­ние от точки C до пря­мой BD_1.

_5. Рас­сто­я­ние между бо­ко­вы­ми реб­ра­ми AA₁ и BB₁ пря­мой тре­уголь­ной призмы ABCA₁B₁C₁ равно 5, а рас­сто­я­ние между бо­ко­вы­ми реб­ра­ми AA₁ и CC₁ равно 8. Най­ди­те рас­сто­я­ние от пря­мой AA₁ до плос­ко­сти BC₁C, если из­вест­но, что дву­гран­ный угол приз­мы при ребре AA₁ равен 60°.

Итоговая контрольная работа

1.  а) Ре­ши­те урав­не­ние

б) Ука­жи­те корни этого урав­не­ния, при­над­ле­жа­ще­го от­рез­ку

2.  В пра­виль­ной четырёхуголь­ной приз­ме SABCD сто­ро­на AB ос­но­ва­ния равна  , а вы­со­та SH пи­ра­ми­ды равна 3. Точки M и N — се­ре­ди­ны рёбер CD и AB, со­от­вет­ствен­но, а NT — вы­со­та пи­ра­ми­ды NSCD с вер­ши­ной N и ос­но­ва­ни­ем SCD.

а) До­ка­жи­те, что точка T яв­ля­ет­ся се­ре­ди­ной SM.

б) Най­ди­те рас­сто­я­ние между NT и SC.

3. Ре­ши­те не­ра­вен­ство:

4. В ост­ро­уголь­ном тре­уголь­ни­ке KMN про­ве­де­ны вы­со­ты KB и NA.

а) До­ка­жи­те, что угол ABK равен углу ANK.

б) Най­ди­те ра­ди­ус окруж­но­сти, опи­сан­ной около тре­уголь­ни­ка ABM, если из­вест­но, что  и ∠KMN = 45°.

5. Жанна взяла в банке в кре­дит 1,2 млн руб­лей на срок 24 ме­ся­ца. По до­го­во­ру Жанна долж­на воз­вра­щать банку часть денег в конце каж­до­го ме­ся­ца. Каж­дый месяц общая сумма долга воз­рас­та­ет на 2 %, а затем умень­ша­ет­ся на сумму, упла­чен­ную Жан­ной банку в конце ме­ся­ца. Суммы, вы­пла­чи­ва­е­мые Жан­ной, под­би­ра­ют­ся так, чтобы сумма долга умень­ша­лась рав­но­мер­но, то есть на одну и ту же ве­ли­чи­ну каж­дый месяц. Какую сумму Жанна вернёт банку в те­че­ние пер­во­го года кре­ди­то­ва­ния?

6. Най­ди­те все зна­че­ния a, для каж­до­го из ко­то­рых су­ще­ству­ет хотя бы одна пара чисел x и y, удо­вле­тво­ря­ю­щих не­ра­вен­ству

7. Из пер­вых 22 на­ту­раль­ных чисел 1, 2, ..., 22 вы­бра­ли 2k раз­лич­ных чисел. Вы­бран­ные числа раз­би­ли на пары и по­счи­та­ли суммы чисел в каж­дой паре. Ока­за­лось, что все по­лу­чен­ные суммы раз­лич­ны и не пре­вос­хо­дят 27.

а) Может ли по­лу­чить­ся так, что сумма всех 2k вы­бран­ных чисел рав­ня­ет­ся 170 и в каж­дой паре одно из чисел ровно в три раза боль­ше дру­го­го?

б) Может ли число k быть рав­ным 11?

в) Най­ди­те наи­боль­шее воз­мож­ное зна­че­ние числа k.

Скачано с www.znanio.ru