Практикум по решению математических задач повышенной сложности для одаренных студентов 1 курса

Федеральное казенное профессиональное образовательное  учреждение "Сиверский техникум-интернат бухгалтеров"

Министерства труда и социальной защиты Российской Федерации

 

 

 

Методическая разработка

 

 

 

 

«Практикум по решению математических задач повышенной сложности для одаренных студентов 1 курса»

 

 

 

Специальность

38.02.01  Экономика и бухгалтерский учет (по отраслям)

 

 

 

 

 

пгт. Сиверский

 

Настоящая  методическая разработка составлена для обучающихся ФКПОУ «Сиверский техникум-интернат бухгалтеров"  Министерства труда и  социальной защиты Российской Федерации  по специальности 38.02.01 Экономика и бухгалтерский учет (по отраслям) для углубленного изучения учебной дисциплины «Математика»

 

 

 

Составитель

Руданец Наталия Васильевна – преподаватель математики  ФКПОУ «Сиверский техникум-интернат бухгалтеров» Министерства труда и  социальной защиты Российской Федерации

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

СОДЕРЖАНИЕ

1.     Пояснительная записка

2.     Содержание программы

3.     Задания для решения

4.     Критерии оценки уровня и качества подготовки студентов.

5.     Список литературы

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1.      Пояснительная записка

Данный курс занятий предназначен для обучающихся 1 курса и направлен на более глубокое изучение разделов математики, предназначен как для дополнения знаний обучающихся, полученных ими на уроках, так и для их углубления.

     Курс предусматривает изучение методов решения уравнений и неравенств с модулем, параметрами, расширение и углубление знаний учащихся по решению тригонометрических, иррациональных, показательных и логарифмических уравнений и неравенств. Большое внимание уделяется задачам с параметрами. Задания данного курса не просты в решении, что позволяет повысить учебную мотивацию обучающихся.

     В результате изучения этого курса будут использованы приемы парной, групповой деятельности для осуществления элементов самооценки, взаимооценки, умение работать с математической литературой и выделять главное.

Цель  курса: Повышение уровня математической подготовки студентов среднего профессионального образования.

Задачи:

1. Развить и укрепить имеющиеся навыки, освоить ранее неизвестные обучающимсяприѐмы и методы решения уравнений и неравенств.

2. Подготовить студентов  к сдаче экзамена и возможности поступления в высшие учебные заведения.

 3. Вызвать интерес к изучаемым темам.

4. Развивать исследовательскую деятельность студентов.

Структура и содержание курса

Курсу отводится 1 час в неделю. Всего 36 часов

 Включенный в программу материал предполагает изучение и углубление следующих разделов математики:

• Уравнения и неравенства.
• Тестовые задачи.
• Формулы тригонометрии.
• Тригонометрические функции и их графики.
• Тригонометрические  уравнения и неравенства.
• Степень с рациональным показателем.
• Степенная функция.
• Показательная функция.
• Логарифмическая функция.

 

Умения и навыки студентов, формируемые  курсом:

·         навык самостоятельной работы с таблицами и справочной литературой;

·         составление алгоритмов решения типичных задач;

·         умения решения тригонометрических, показательных и логарифмических уравнений и неравенств;

 

Особенности курса:

1.      Краткость изучения материала.

2.      Практическая значимость для студентов.

3.      Нетрадиционные формы изучения материала.

 

Формы организации учебных занятий

   Формы проведения занятий включают в себя лекции, практические работы. Основной тип занятий  комбинированный урок. Каждая тема курса начинается с постановки задачи. Теоретический материал излагается в форме мини -  лекции. После изучения теоретического материала выполняются задания для активного обучения, практические задания для  закрепления, выполняются практические работы в рабочей тетради, проводится работа с тестами.

   Систематическое повторение способствует более целостному осмыслению изученного материала, поскольку целенаправленное обращение к изученным ранее темам позволяет обучающимся встраивать новые понятия в систему уже освоенных знаний.

Контроль и система оценивания

  Текущий контроль уровня усвоения материала осуществляется на каждом занятии по результатам выполнения обучающимися самостоятельных, практических и тестовых  работ.

 

2.      Содержание программы

Программа  курса рассчитана на один год обучения и содержит следующие темы:

1.      «Уравнения и системы уравнений»

Способы решения различных уравнений (линейных, квадратных и сводимых к ним, дробно-рациональных). Рациональные уравнения, приводящиеся с помощью преобразований к линейным и квадратным. Иррациональные уравнения. Нахождение рациональных корней многочлена с целыми коэффициентами. Разложение на множители. Системы уравнений. Уравнения, содержащие абсолютные величины.

2.      «Неравенства»

 Преобразование неравенств. Неравенства, содержащие абсолютные величины. Способы         решения различных неравенств (числовых, линейных, квадратных). Метод

 интервалов. Область определения выражения.

3.      «Текстовые задачи»

Задачи на проценты. Задачи на «движение», на «концентрацию», на «смеси и  

 сплавы», на «работу». Выбор неизвестных. Составление уравнений (ограничений).

Решение нестандартных задач.

4.      «Квадратный трехчлен»

Существование корней квадратного уравнения. Знаки корней. Расположение корней

 квадратного трехчлена. Взаимное расположение корней двух квадратных трехчленов. Уравнения, неравенства и системы с параметром. Графические интерпретации. Задачи на максимум-минимум. Доказательство неравенств.

5.                  « Формулы тригонометрии». 

Формулы  приведения, сложения, двойных углов и их применение. Применение основных тригонометрических формул к преобразованию выражений.

6.                  «Тригонометрические функции и их графики».

Обобщить понятие тригонометрических функций; свойства функций и умение строить графики.

7.                  «Тригонометрические  уравнения и неравенства».

Сформировать умения решать простейшие тригонометрические уравнения; ознакомить с некоторыми приемами решения тригонометрических уравнений.

8.                  « Степенная функция».

Обобщить понятие степенной функцией с действительным показателем, ее свойства и умение строить ее график; знакомство с разными способами решения иррациональных уравнений; обобщение понятия степени числа и корня  n-й степени.

9.                  «Показательная функция».

Систематизировать понятие показательной  функции; ее свойств и умение строить ее график; познакомиться со способами решения показательных  уравнений и неравенств.

10.              «Логарифмическая функция». 

Обобщить понятие логарифмической функции; ее свойства и умение строить ее график; знакомство с разными способами решения  логарифмических уравнений и неравенств.

11.              « Задачи с геометрическим содержанием». 

Действия с геометрическими фигурами, координатами и векторами. Планиметрические задачи на нахождение геометрических величин (длин, углов, площадей).

12.    «Планиметрия»

Построение чертежа. Выявление характерных особенностей заданной конфигурации. Опорные задачи. Геометрические методы решения задач. Аналитические методы. Метод координат. Векторный метод.

13. «Стереометрия».

Построение чертежей многогранников, тел вращения. Построение сечений. Решение задач на вычисление площадей поверхностей тел, объемов.

 

 

 

 

2.1 Учебно-тематический план

    

 

3.      Задания для решения

I.                   Самостоятельная работа (разноуровневая) .

I уровень: учащиеся выполняют задание теста по вариантам.

I вариант.

1. Вычислите: .

1) 1;   2) 4,5;   3) 8;   4) 21.

2. Вычислите: .

1) ;   2) −0,2;   3) −0,4;   4) .

3. Упростите выражение: .

1) 3;   2) −15;   3) −3;   4) 9.

4. Упростите выражение:  .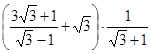

1) 2;   2) ;   3) ;   4) .

II уровень: учащиеся выполняют задания, требующие подробного описания решения

1) Упростите выражение: .

2) Вычислите: .

3) Упростите выражение:  .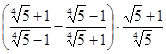

Часть В

1.   Вычислите      при  m =  – .

2.   Решите уравнение   = х – 4 .

3.   Сократите  дробь       

 

Часть С

1.   Упростите         

2.   Решите  уравнение     

 

 

(Иррациональные  уравнения)

Решите  уравнения

Вариант 1                                                  Вариант 2

1)      2)      3)      4)      5)      6*) 7*) 1)      2)      10) 11)

1)      2)      3)      4)      5)      6*) 7*) 8) 9)  10) 11)

 

Практическое занятие

 (Иррациональные  неравенства)

Решите  неравенства

Вариант1                                                   Вариант 2

1)      2)      3)      4)      5)      6)      7)      8)      9*) 10*) 11*)

1)      2)      3)      4)      5)      6)      7)      8)      9*) 10*) 11*)

12) При  каких значениях  р  решением  неравенства  является  промежуток?

; [2;18)

;  [–1;15)

 

Практическое занятие

 (Системы  уравнений)

Вариант № 1             Вариант № 2           Вариант № 3*   

Решите системы  уравнений

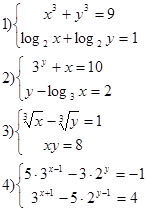
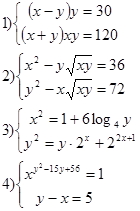
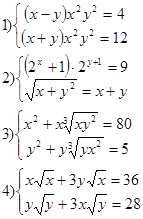
5*)  При  каких значениях  р система неравенств  не  имеет  решений?

 

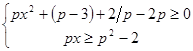
Тест по теме «Показательная функция.

 

Показательные уравнения и неравенства»

 

1)      Установите соответствие между показательным уравнением и методом его решения.

Показательное уравнение	Метод  решения
	А) функционально -графический
	В)введения новой переменной
	С)    вынесение общего множителя за скобки
	D)    приведение к общему основанию
	Е) группировка

2)   Укажите промежуток, содержащий корень уравнения

А) (-3;1)          В) [-2; 0)         C) [2; 5]          D) [0; 2]          E) [2;5).

3) Найти сумму корней или корень (если он один) уравнения

              А) 0                 В) 7           С) 1           D) -1               Е) 2.

4)  Найти наименьшее целое число, которое является  решением  неравенства .

А) 0                 В) -1         С) 1           D) 2                 Е) -2.

5) Найти область определения функции .

A) B)   )         C) [0; +D) [)         E) [0; ].

Практическое занятие 

 (Показательная  функция)

Вариант № 1                                           Вариант № 2

1)  Изобразите  схематически  график  и  опишите  свойства  функции

у =

у =

2)  Постройте график функции  у = 2^х – 1 (у = 3^х – 1); назовите  множество  значений  функции; выделите  на  рисунке  часть  графика, для  которой

 – 1/2 <y< 3 (– 2/3 <y< 2), и  найдите  соответствующие  значения  х.

3*)  Постройте  график  функции  у =  (у = ) и  найдите  наименьшее и наибольшее значение этой  функции на отрезке [–2; 4] ([–2; 2])

4)  Решите  графически  уравнение

(1/2)х = 2 – х

3х = 2х + 3

5)  Решите  графически  неравенство

3х< 1/3

(1/2)х> 2

Практическое   занятие

 

Показательные уравнения

 

Вариант 1.

Найдите корень уравнения

1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 

 

 

Часть В

1.   Решите  уравнение : + 2 – 15 = 0.

2.  Найдите  наименьшее значение функции у =     на  отрезке [ – 3 ;2].

3.  Найдите корень уравнения, а если их несколько, то их среднее арифметическое

=

Часть С

1.  Найдите наибольшее решение неравенства  

2.  Решите систему  уравнений    

                                                                       у² – у  =  –  12.

 

 

Практическое занятие 

 

 (Показательные  неравенства)

     Вариант № 1                                       Вариант № 2

Решите  неравенства

1)      2)      3)      4)      5)      6)      7)      8)

1) 2) 3) 4)  5) 6)  7)  8)

 

 

(Логарифмическая  функция)

Вариант № 1                                                Вариант № 2

1)  Изобразите  схематически  график  и  опишите  свойства  функции 

у = logx

у = logx

1*)  Изобразите  схематически  график

y =log0,4(–x); y =; у =log2log241-x

y =lg; y =; y =lglg10x+1

2)  Постройте  график  функции  у = log₂x – 1 ( у = log₂(x – 1)); назовите  множество  значений  функции; выделите  на  рисунке  часть  графика, для  которой  – 2 <y< 1 (– 1<y< 2), и  найдите  соответствующие  значения  х.

3*)  Постройте  график  функции  у =  (у = ) и  найдите  наименьшее и наибольшее значение этой  функции на отрезке [0,5;8] ([1,5;9])

4)  Решите  графически  уравнение

log3x = 2x – 3

log1/2x = – 0,5x + 1

5)  Решите  графически  неравенство

log1/2x> –3

log3x< 2

 

6.      Решите систему неравенств: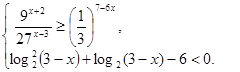

 

Тригонометрия

Вариант  1

Часть А

1.  Найдите множество значений функции у = 3 – 2sinx

1)      [ 1; 5];       2)     [ - 1; 1];         3)      [ 3; 5 ];                  4)    [ 1; 3].

          2.  Вычислите  значение  sin2x, если  cosx =   и  

1)       –    ;          2)     ;                  3)     ;                          4) –     .

          3.  Найдите сумму всех целых чисел, которые входят в область значений функции     у = 4cos²x – 7

1)      – 25;               2)  25;                   3)      – 22;                       4)   0.

4.   Упростите  выражение   5sin²x – 4 + 5cos²x

1)       1;                   2)   9;                     3)     – 9;                         4)  – 4.

5.   Решите уравнение      cosx –  = 0

1)       2)    3)      4)  

Часть В

1.  Найдите значение выражения        при 

2.  Упростите  выражение    

3.  Определите, сколько корней уравнения   2сos²x + 7cosx – 4 = 0, принадлежит отрезку [ - 2

ЧастьС

1.  Найдите наибольший отрицательный корень уравнения ( в градусах)

sin3xcos5x – cos3xsin5x = 0,5

2.  Решите уравнение     sin²x +   – 2 = 0

 

Текстовые задачи

1.      Решите задачу, выделяя три этапа математического моделирования.
Для ремонта квартиры купили 23 рулона обоев. На спальную комнату обоев потратили на 3 рулона обоев больше, чем на коридор. Для ремонта столовой обоев понадобилось в три раза больше, чем на ремонт коридора. Сколько рулонов обоев понадобилось для ремонта столовой?

2.       Решите задачу, выделяя три этапа математического моделирования.
Три учителя проверили 107 экзаменационные работы. Один из учителей проверил на 9 работ больше чем другой и в два раза меньше, чем третий. Сколько работ проверил каждый учитель?

3.      Владелец дискотеки имел стабильный доход. В погоне за увеличением прибыли он повысил цену на билеты на 25%. Количество посетителей резко уменьшилось, и он стал нести убытки. Тогда он вернулся к первоначальной цене билетов. На сколько процентов владелец дискотеки снизил новую цену билетов, чтобы она стала равна первоначальной?

4.      За год стипендия студента увеличилась на 32%. В первом полугодии стипендия увеличилась на 10%. Определите, на сколько процентов увеличилась стипендия во втором полугодии.

5.       В процессе физического эксперимента давление газа в сосуде изменялось трижды. Первый раз давление газа увеличивалось на 50%, а во второй и третий раз уменьшалось на 20% и 40% соответственно. Определите, на сколько кПа уменьшилось давление газа в сосуде к концу эксперимента, если в начале эксперимента оно было равно 200 кПа.

6.       Денежный вклад в банк за год увеличивается на 12%. Вкладчик открыл счёт на 15000 рублей. Через год он решил снять со счёта некоторую часть денег. Какую наибольшую сумму может снять со счёта вкладчик, если он хочет, чтобы в конце второго года на его счёте оказалось не менее 10000 рублей? (Ответ округлите до целого числа.)

7.       Магазин выставил на продажу товар с наценкой 60% от закупочной цены. После продажи половины всего товара магазин снизил назначенную цену на 30% и распродал оставшийся товар. Сколько процентов от закупочной цены товара составила прибыль магазина?

8.      Билет стоит 20 рублей. Ожидается повышение цены на 30 %. Сколько билетов можно будет купить на 100 рублей после повышения цены?  Объёмы ежемесячной продажи телевизоров в первом, втором и третьем магазинах сети относятся ка 5 : 8 : 10. Планируется уменьшить ежемесячную продажу телевизоров в первом магазине на 11% и во втором - на 5%. На сколько процентов нужно увеличить объём ежемесячной продажи телевизоров в третьем магазине, чтобы суммарный объём ежемесячной продажи телевизоров увеличился на 3%?

9.      Объемы ежегодной добычи нефти первой, второй и третьей скважинами относятся как 6 : 7 : 10. Планируется уменьшить годовую добычу нефти из первой скважины на 10% и из второй – тоже на 10%. На сколько процентов нужно увеличить годовую добычу нефти из третьей скважины, чтобы суммарный объем добываемой за год нефти не изменился?

10.   Бассейн полностью заполняется водой за 6 часов с помощью трёх насосов, мощности которых относятся как 4:5:6. Сколько процентов объема бассейна будет заполнено за 5 часов 15 минут совместной работы первого и второго насосов?

11.  Студент приобрёл с учётом скидки в 28 %  компьютер  за 18600 рублей. Какова стоимость компьютера без скидки?

12.  Новейший процессор фирмы Intel стоит 7800 рублей, что на 15 % превышает цену на предыдущую модель. Сколько стоит предыдущая модель?

13.  Двое работников выполнили определённую работу за 12 дней, при этом последние 2 дня первый работник не работал. За сколько дней первый работник выполнит всю работу, если известно, что за время совместной работы они выполнили 90% всего задания?

14.  Цену мониторов снизили на 20 % , а затем новую цену снизили на 25 % . На сколько процентов  уменьшилась первоначальная стоимость мониторов?

15.  Сборочный конвейер увеличил свою производительность на 20 % , а потом ещё раз на  5 % . На сколько процентов увеличилась производительность конвейера в сравнении с первоначальной?

16.  Подарочный набор для женщин первоначально стоил  600  руб. Однако, за неделю до 8 марта было решено снизить цену на 15 % , затем 7 марта новую цену снизили ещё на 12 % . Определить, по какой цене продавали набор 8 марта и на сколько процентов эта цена снизилась по сравнению с первоначальной.

17.   В связи с выпуском нового товара фирма установила первоначальную цену в 900 грн., что не соответствовало реальной стоимости этого товара. Через месяц, в связи с ростом спроса на этот товар, было решено повысить цену на него на 10 % , а затем через две недели новую цену повысили ещё на 5 % . Определить, по какой цене стал продаваться товар и на сколько процентов выросла его первоначальная цена?

18.  В связи с повышением спроса на товар, первоначальная цена которого составляла 320 грн., магазин решил повысить цену товара на 30 % . После этого спрос на товар резко упал и поэтому магазин для повышения спроса решил снизить цену на 10 %. Определить конечную цену товара и установить, на сколько процентов и в какую сторону она изменилась по сравнению с первоначальной (возросла или уменьшилась).

19.   Брокерская фирма приобрела два пакета акций, а затем продала их за общую сумму 21 миллион 680 тысяч рублей, получив при этом 28% прибыли. За какую сумму фирма приобрела каждый из пакетов акций,  если при продаже первого пакета прибыль составила 40%,  а при продаже второго - 20%?

20.  В магазине одежды проводилась распродажа. Костюмы продавались со скидкой 20%, плащи - со скидкой 40%. Покупатель купил костюм и плащ за 6900 рублей в сумме, заплатив на 32% меньше их суммарной первоначальной цены. Найдите первоначальные цены костюма и плаща.

21.  В команде "Шахтёр" процент травмированных футболистов накануне игр Лиги Чемпионов оказался в пределах от 2,5 % до 2,6 %. Каково минимально возможное количество игроков числится в команде?

Критерии оценки уровня и качества подготовки студентов

Преподаватель и студент  на этих занятиях не видят нужды в отметках. Студенты  занимаются не ради них. Им интересен сам процесс творчества, поиска, познания. При этом у студентов проявляется высокая учебно-познавательная мотивация и активность, которые детерминированы следующими причинами: личным выбором  дополнительных занятий, индивидуальными потребностями и интересами обучающегося, харизмой преподавателя, личной значимостью предложенного на занятиях материала.

 

Субъектами оценки на факультативном занятии являются каждый студент  в отдельности, студенты  всей группы, сам преподаватель.

 

Обучение может стать безотметочным, если оно строится по следующим правилам:

·             отметка отсутствует, но содержательная оценка обязательна;

·             студенты  пользуются ориентирами для самооценки, которые для них являются предельно понятными;

·             самооценка студента предшествует оценке преподавателя.

Дидактическими  средствами, применение которых на дополнительных занятиях позволяет обеспечить эффективную оценочную деятельность студентов и преподавателя могут быть:

1) «Оценочный лист». Обучающемуся предлагается заполнить таблицу, в левой колонке которой вписаны учебные элементы темы (табл. 1).

Таблица 1

Лист самооценки знаний

Мои выводы: ______________________________________________

 

2)«Самооценка уровня владения умениями (исследовательскими, работы с текстом, решения задач и т.п)». Предлагается оценить свои умения, что студент делает в процессе заполнения таблицы (табл. 2).

Таблица 2

Лист самооценки умений

Мои выводы: _______________________________________________

3)«Мои  образовательные достижения».

Студенту предлагается вести дневник, в котором, в частности, он может записывать, чего достиг при изучении дополнительных занятий (табл. 3).

Таблица 3

Мои образовательные достижения

Мои планы: ________________________________________________

 

 

 

 

 

 

Список литературы

 

1) «Алгебра и начала анализа 10 – 11». Автор Ш. А. Алимов. Москва «Просвещение», 2010 г.

2) «Геометрия 10 – 11». Автор Л. С. Атанасян. Москва «Просвещение», 2013 г.

3)А. Г. Мордкович, П. В. Семенов. Алгебра и начала анализа. 10 класс, 11 класс: задачник для общеобразовательных учреждений (профильный уровень)- М.: Мнемозина, 2012

4) Книга для учителя. Изучение геометрии в 10-11 классах.

Авторы: С.М. Саакян, В.Ф. Бутузов. – М.: Просвещение, 2004.

5) Алгебра и начала анализа. Дидактические материалы для 10-11 классов. Авторы: М.И.Шабунин, М.В.Ткачева и другие. М: Мнемозина, 2010.

6) Алгебра и начала анализа 10-11 классы. Самостоятельные и контрольные работы.

Авторы: А.П.Ершова, В.В.Голобородько. М: Илекса, 2012.

7) Изучение сложных тем курса алгебры в средней школе: Учебно – методические материалы по математике. – М.: Илекса, Ставрополь: Сервисшкола, 2006.

8) Колесникова С. И. Математика. Решение сложных задач Единого государственного экзамена. – М.: Айрис-пресс, 2005.

9) Тематические тесты. Математика. ЕГЭ-2015. 10-11 классы/ Под редакцией Ф. Ф. Лысенко. – Ростов-на-Дону: Легион, 2011.

10) Тестовые контрольные задания по алгебре и началам анализа./ Под редакцией   Е. А. Семенко. – Краснодар: «Просвещение – Юг», 2005.

Интернет-ресурсы:

Демоверсии ЕГЭ по математике.

 

Скачано с www.znanio.ru