Элементы комбинаторики

Филиал бюджетного профессионального образовательного учреждения Чувашской Республики

«Чебоксарский медицинский колледж»

Министерства здравоохранения Чувашской Республики в городе Канаш

 

РАССМОТРЕНО и ОДОБРЕНО  на заседании  ЦМК ОГСЭ дисциплин Протокол № ____       от «___» ___________ 20 ___ г. Председатель ___________ Л.М. Иванова

 

 

 

 

 

 

 

 

 

Свойства и график функции у =sin x, y = cos x

специальность 34.02.01 Сестринское дело (базовая подготовка)

учебная дисциплина БД.04 Математика

 

 

 

 

 

 

 

 

 

              

Составил: Семенова А.М., преподаватель математики филиала БПОУ «Чебоксарский медицинский колледж» Министерства здравоохранения Чувашии в г Канаш

                 

 

 

 

Канаш, 2020

 

 

 

Личностных:

Л1. Сформированность представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, идеях и методах математики;

Л2. Понимание значимости математики для научно-технического прогресса, сформированность отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей;

Л8. Отношение к профессиональной деятельности как возможности участия в решении личных, общественных, государственных, общенациональных проблем;

метапредметных:

М1. Умение самостоятельно определять цели деятельности и составлять планы деятельности; самостоятельно осуществлять, контролировать и корректировать деятельность; использовать все возможные ресурсы для достижения поставленных целей и реализации планов деятельности; выбирать успешные стратегии в различных ситуациях;

М5. Владение языковыми средствами: умение ясно, логично и точно излагать свою точку зрения, использовать адекватные языковые средства;

М7. Целеустремленность в поисках и принятии решений, сообразительность и интуиция, развитость пространственных представлений; способность воспринимать красоту и гармонию мира;

 предметных:

П1. Сформированность представлений о математике как части мировой культуры и месте математики в современной цивилизации, способах описания явлений реального мира на математическом языке;

П2. Сформированность представлений о математических понятиях как важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий;

П5. Сформированность представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Элементы комбинаторики

1. Элементы комбинаторики.

2.Общие правила комбинаторики.

3.Генеральная совокупность без повторений и выборки без повторений.

4.Применение графов (схем) при решении комбинаторных задач.

 

1.Комбинаторика и ее возникновение.

 

Комбинаторика- это область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов, принадлежащих данному множеству.

 

Комбинаторика возникла в XVI веке. В жизни привилегированных слоев тогдашнего общества большое место занимали азартные игры (карты, кости). Широко были распространены лотереи. Первоначально комбинаторные задачи касались в основном азартных игр: сколькими способами можно получить данное число очков, бросая 2 или 3 кости или сколькими способами можно получить 2-ух королей в некоторой карточной игре. Эти и другие проблемы азартных игр являлись движущей силой в развитии комбинаторики и далее в развитии теории вероятностей.

Одним из первых занялся подсчетом числа различных комбинаций при игре в кости итальянский математик Тарталья. Он составил таблицы (числа способов выпадения k очков на r костях). Однако, он не учел, одна и та же сумма очков может выпасть различными способами, поэтому его таблицы содержали большое количество ошибок.

Теоретическое исследование вопросов комбинаторики предприняли в XVII веке французские математики Блез Паскаль и Ферма. Исходным пунктом их исследований были так же проблемы азартных игр.

Дальнейшее развитие комбинаторики связано с именами Я. Бернулли, Г. Лейбница, Л. Эйлера. Однако, и в их работах основную роль играли приложения к различным играм.

Сегодня комбинаторные методы используются для решения транспортных задач, в частности задач по составлению расписаний, для составления планов производства и реализации продукции и т.д

2.      Общие правила комбинаторики.

 

Правило суммы: Если некоторый объект А может быть выбран m способами, а объект В- k способами, то объект «либо А, либо В» можно выбрать m+k способами.

Примеры:

1.              Допустим, что в ящике находится n разноцветных шаров. Произвольным образом вынимается 1 шарик. Сколькими способами это можно сделать? 

Ответ: n способами.

Распределим эти n шариков по двум ящикам: в первый- m шариков, во второй- k шариков. Произвольным образом из произвольно выбранного ящика вынимается 1 шарик. Сколькими способами это можно сделать?

Решение: Из первого ящика шарик можно вынуть m способами, из второго- k способами. Тогда всего способов m+k=n.

 

2.      Морской семафор.

В морском семафоре каждой букве алфавита соответствует определенное положение относительно тела сигнальщика двух флажков. Сколько таких сигналов может быть?

Решение: Общее число складывается из положений, когда оба флажка расположены по разные стороны от тела сигнальщика и положений, когда они расположены по одну сторону от тела сигнальщика. При подсчете числа возможных положений применяется правило суммы.

Правило произведения:  Если объект А можно выбрать m способами, а после каждого такого выбора другой объект В можно выбрать (независимо от выбора объекта А) k способами, то пары объектов «А и В» можно выбрать m*k способами.

Примеры:

1.      Сколько двузначных чисел существует?

Решение: Число десятков может быть обозначено любой цифрой от 1 до 9. Число единиц может быть обозначено любой цифрой от 0 до 9. Если число десятков равно 1, то число единиц может быть любым (от 0 до 9). Таким образом, существует 10 двузначных чисел, с числом десятков- 1.  Аналогично рассуждаем и для любого другого числа десятков. Тогда можно посчитать, что существует 9 *10 = 90 двузначных чисел. 

2.            Имеется 2 ящика. В одном лежит m разноцветных кубиков, а в другом- k разноцветных шариков. Сколькими способами можно выбрать пару «Кубик-шарик»?

Решение: Выбор шарика не зависит от выбора кубика, и наоборот. Поэтому, число способов, которыми можно выбрать данную пару равно m*k.

 3.      Генеральная совокупность без повторений и выборки без повторений.

 

Генеральная совокупность без повторений- это набор некоторого конечного числа различных элементов a₁, a₂, a₃, ..., a_n.

Пример: Набор из n разноцветных лоскутков.

Выборкой объема k (k n) называется группа из m элементов данной генеральной совокупности.

Пример: Пестрая лента, сшитая из m разноцветных лоскутков, выбранных из данных n.

Размещениями из n элементов по k называются такие выборки, которые содержат по k элементов, выбранных из числа данных n элементов генеральной совокупности без повторений, и отличаются друг от друга либо составом элементов, либо порядком их расположения.

- число размещений из n по k.

Число размещений из n по k можно определить следующим способом: первый объект выборки можно выбрать n способами, далее второй объект можно выбрать n-1 способом и т.д.

Преобразовав данную формулу, имеем:

Следует помнить, что 0!=1.

 

Примеры:

1.                      В первой группе класса А первенства по футболу участвует 17 команд. Разыгрываются медали: золото, серебро и бронза. Сколькими способами они могут быть разыграны?

Решение: Комбинации команд-победителей отличаются друг от друга составом и порядком следования элементов, т.е. являются размещениями из 17 по 3.

2.                      Научное общество состоит из 25-ти человек. Необходимо выбрать президента общества, вице-президента, ученого секретаря и казначея. Сколькими способами это можно сделать?

Решение: Комбинации руководящего состава общества отличаются друг от друга составом и порядком следования элементов, т.е. являются размещениями из 25 по 4.

Перестановками без повторений из n элементов называются размещения без повторений из n элементов по n, т.е. размещения отличаются друг от друга только порядком следования элементов.

- число перестановок.

Примеры:

1.                      Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5 при условии, что они должны состоять из различных цифр?

Решение: Имеем перестановки из 5 элементов.

2.      Сколькими способами можно собрать 6 разноцветных лоскутков в пеструю ленту?
Решение: Имеем перестановки из 6 элементов.

 

Сочетаниями без повторений из n элементов по k называются такие выборки, которые содержат по k элементов, выбранных из числа данных n элементов генеральной совокупности без повторений, и отличаются друг от друга только составом элементов.

 

 -число сочетаний из n по k 

Элементы каждого из   сочетаний можно расставить  способами. Тогда

Примеры:

1.       Если в полуфинале первенства по шахматам участвует 20 человек, а в финал выходят лишь трое, то сколькими способам и можно определить эту тройку?

Решение: В данном случае порядок, в котором располагается эта тройка, не существенен. Поэтому тройки, вышедшие в финал, являются сочетаниями из 20 по 3.

2.      Сколькими способами можно выбрать трех делегатов из десяти человек на конференцию?

Решение: В данном случае порядок, в котором располагается эта тройка, не существенен. Поэтому тройки делегатов являются сочетаниями из 10 по 3.

Конспект:

    

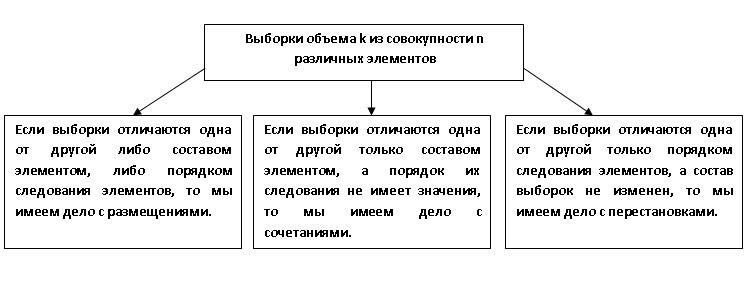
4.  Применение графов (схем) при решении комбинаторных задач.

В случае, когда число возможных выборов на каждом шагу зависит от того, какие элементы были выбраны ранее, можно изобразить процесс составления комбинаций в виде «дерева». Сначала из одной точки проводят столько отрезков, сколько различных выборов можно сделать на первом шагу. Из конца каждого отрезка проводят столько отрезков, сколько можно сделать выборов на втором шагу, если на первом шагу был выбран данный элемент и т.д.

 

Задача:

При составлении команд космического корабля учитывается вопрос и психологической совместимости участников путешествия. Необходимо составить команду космического корабля из 3 человек: командира, инженера и врача. На место командира есть 4 кандидата: a₁, a₂, a₃, a₄.  На место инженера- 3: b₁, b₂, b₃. На место врача- 3: c₁, c₂, c₃. Проведенная проверка показала, что командир a₁ психологически совместим с инженерами b₁ и b₃  и врачами c₁ и c₃. Командир a₂ - с инженерами b₁ и b₂. и всеми врачами. Командир  a₃ - с инженерами b₁ и b₂ и врачами c₁ и c₃. Командир a₄-со всеми инженерами и врачом  c₂. Кроме того, инженер b₁ не совместим с врачом c₃, b₂- с врачом c₁ и b₃- с врачом c₂. Сколькими способами при этих условиях может быть составлена команда корабля?

 

Решение:

 Составим соответствующее «дерево».

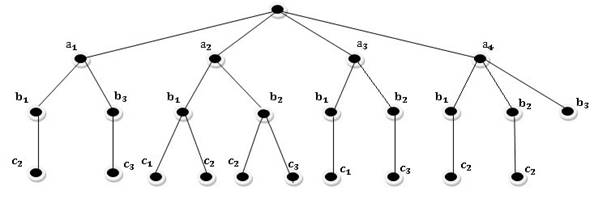
 Ответ: 10 комбинаций.

 

Такое дерево является графом и применяется для решения комбинаторных задач.

Контрольная работа по теме: «Элементы теории вероятностей»

Вариант I.

18

1. В ящике 10 перенумерованных шаров с номерами от 1 до 10. Вынули

один шар. Какова вероятность того, что номер вынутого шара не

превышает 10?

2. Монета подброшена два раза. Какова вероятность того, что оба раза

выпадет герб?

3. Три стрелка независимо друг от друга стреляют по цели. Вероятность

попадания в цель для первого стрелка равна 0,75, для второго – 0,8, для

третьего – 0,9. Определить вероятность того, что все три стрелка

одновременно попадут в цель.

4. В клетке есть пушистые и гладкошёрстые хомяки. Среди пушистых 3

белых, 2 чёрных и 4 рыжих. Среди гладкошёрстых 2 белых, 3 чёрных и

1 - рыжий. Какова вероятность того, что выбранный наугад хомяк

будет белым или пушистым?

5. В трёх одинаковых коробках лежат жетоны. В первой коробке – 2

жёлтых и 3 красных, во второй коробке – 3 жёлтых и 4 красных, в

третьей – 1 жёлтый и 5 красных. Какова вероятность того, что из

наугад выбранной коробки будет извлечён жёлтый жетон?

Вариант II.

1. В ящике 10 перенумерованных шаров с номерами от 1 до 10. Вынули

один шар. Какова вероятность того, что номер вынутого шара

превышает 10?

2. В лотерее 2000 билетов. На один билет падает выигрыш 100 рублей, на

4 билета – выигрыш по 50 рублей, на 10 билетов – выигрыш по 20

рублей, на 20 билетов – выигрыш по 10 рублей, на 165 билетов –

выигрыш по 5 рублей, на 400 билетов – выигрыш по 1 рублю.

Остальные билеты невыигрышные. Какова вероятность выиграть по

билету не менее 10 рублей?

19

3. В первом ящике 2 белых и 10 чёрных шаров; во втором ящике 8 белых

и 4 чёрных шара. Из каждого ящика вынули по шару. Какова

вероятность того, что оба шара белые?

4. Бросают игральную кость. Какова вероятность того, что выпадет 3 очка

или нечётное число очков?

5. В двух одинаковых аквариумах живут чёрные и красные рыбки. В

первом – 3 красных и 5 чёрных рыбок, а во втором – 4 красных и 2

чёрных. Какова вероятность того, что из наугад выбранного аквариума

будет выловлена сачком чёрная рыбка?

20

Используемая литература.

1. Баврин И.И. Высшая математика. Учебник для студентов

естественнонаучных специальностей педагогических вузов. – М.:

Академия, 2010

2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. – Высшая математика в

упражнениях и задачах. М.,: Высш. шк., 1999.

3. Кутасов А.Д. и др. – Пособие по математике для поступающих в вузы.

М.: Наука, 1985.

4. Цыпкин А.Г., Пинский А.И. – Справочное пособие по методам

решения задач по математике. М.: Наука 1989.

5. Богомолов Н.В. – Практические занятия по математике. М.,:

Издательство Юрайт, 2013.

6. Гусак А.А. – Высшая математика. Минск: ТетраСистемс, 2004.

7. Вентцель Е.С. – Теория вероятностей. М.,: Высш. шк., 2001.

8. Стойлова Л.П. –Математика. М.,: Издательский центр Академия., 2002.

9. Лысенко Ф.Ф., Калабухова С.Ю. - Математика. Подготовка к ЕГЭ.

Элементы теории вероятностей. Ростов-на-Дону, ЛЕГИОН-М, 2011.

 

Скачано с www.znanio.ru