Элементы теории вероятностей

Практическая работа №10

Тема: «Элементы теории вероятностей»

 

Цель: уметь применять формулы теории вероятностей при решении задач.

 

Оборудование: ручка, методические рекомендации по выполнению работы.

 

Методические рекомендации по выполнению практической работы:

Задание №1.

В группе из 15 учащихся, 9 девочек и 6 мальчиков на экзамене по математике имеется один счастливый билет. Наудачу отбирается 5 девочек и 3 мальчика, какова вероятность, что среди них есть обладатель счастливого билета.

 

Решение:

Пусть событие А – «что среди отобранных 5 девочек и 3 мальчиков есть обладатель счастливого билета».

Так как в группе конечное число человек, то применима классическая формула вероятности: .

По условию задачи в группе 15 учащихся, то есть n=15, из которых наудачу отбирают 8=5+3 учащихся, то есть m=8, так как порядок следования учащихся в подгруппе из восьми человек не важен, то будем использовать формулу сочетаний, для нахождения всевозможного числа исходов нашего испытания:

Получим:

.

 

Найдем теперь число исходов, благоприятствующих наступлению нашего испытания М, так как 5 девочек мы можем выбрать только из 9 имеющихся в группе девочек, а 3 мальчика – соответственно из 6 мальчиков рассматриваемой группы, причем нужно выбрать одновременно и девочек и мальчиков, то по правилу умножения получим:

 

 

Таким образом, искомая вероятность равна:

Ответ: 0,39.

 

Задание №2.

Экзаменационный билет содержит 4 вопроса. Вероятность правильно ответить на 1-ый вопрос, у некоторого студента, равна 0,6; на 2-ой вопрос – 0,7; на 3-ий – 0,8; на 4-ый – 0,9. Экзамен считается сданным, если студент правильно ответит хотя бы на три вопроса в билете. Найти вероятность того, что экзамен студентом сдан.

 

Решение:

Пусть событие А – «Экзамен студентом сдан»

По условию задачи известны вероятности правильного ответа на 1-ый, 2-ой, 3-ий и 4-ый вопросы в экзаменационном билете некоторым студентом соответственно, а именно:

;

;

;

.

Найдем теперь вероятности противоположных событий, а именно вероятности неправильного ответа на 1-ый, 2-ой, 3-ий и 4-ый вопросы в экзаменационном билете некоторым студентом, они соответственно равны:

Наше событие А – «Экзамен студентом сдан», является сложным событием, так как экзамен считается сданным, если студент правильно ответит хотя бы на три вопроса в билете, что означает студент должен правильно ответить либо на три из четырех вопросов, либо на все четыре вопроса правильно, то есть наше событие представим виде суммы простых событий:

, где события  – «студент правильно ответит на три из четырех вопросов в билете»;

 – «студент правильно ответит на все четыре вопроса в билете».

Так как события  и  несовместны, то справедлива формула:

Найдем вероятности событий  и , используя таблицы:

 – «студент правильно ответит на три из четырех вопросов в билете»

1-ый вопрос	2-ой вопрос	3-ий вопрос	4-ый вопрос
(+)	(+)	(+)	(-)
(+)	(+)	(-)	(+)
(+)	(-)	(+)	(+)
(-)	(+)	(+)	(+)

 

Таким образом,

 

 

 

 – «студент правильно ответит на все четыре вопроса в билете»

1-ый вопрос	2-ой вопрос	3-ий вопрос	4-ый вопрос
(+)	(+)	(+)	(+)

Таким образом,

 

Искомая вероятность равна:

 

Ответ: 0,7428.

 

Задание №3.

На двух станках обрабатываются однотипные детали. Вероятность брака для станка №1 составляет 0,03, для станка № 2 – 0,02. Обработанные детали складываются в одном месте, причем деталей, обработанных на станке № 1, вдвое больше, чем деталей, обработанных на станке № 2. Найти вероятность того, что: а) взятая наугад деталь будет стандартной; б) наугад взятая стандартная деталь изготовлена на первом станке.

 

Решение:

Пусть событие А – «взятая наугад деталь будет стандартной».

Предположим гипотезы:

 – деталь изготовлена первым станком;

 – деталь изготовлена вторым станком.

Пусть x – количество деталей, изготавливаемых на станке № 2, тогда количество деталей, изготавливаемых на станке № 1, будет равно 2x.

Таким образом,

Получаем, что  – вероятности того, что деталь изготовлена первым и вторым станком соответственно.

Найдем теперь условные вероятности того, что деталь, изготовленная на первом и втором станке соответственно, будет стандартной:

а) по формуле полной вероятности получаем:

 

 

б) по формуле Байеса найдем вероятность тог, что наугад взятая стандартная деталь изготовлена на первом станке, а именно:

 

 

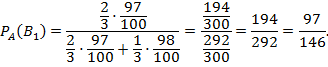
Ответ: а) ;  б) .

 

Задание №4.

Наблюдение за районом осуществляется тремя радиолокационными станциями (РЛС). В район наблюдений попал объект, который обнаруживается любой РЛС с вероятностью 0,2.

Построить ряд распределения, найти функцию распределения, математическое ожидание, дисперсию и среднее квадратичное отклонение числа РЛС, обнаруживших объект.

 

Решение:

Пусть случайная величина X – число РЛС, обнаруживших объект.

Найдем возможные значения СВ X:

 – ни одна из трех РЛС не обнаружила объект;

 – одна из трех РЛС обнаружила объект;

 – две из трех РЛС обнаружили объект;

 – все три РЛС обнаружили объект.

Найдем теперь соответствующие вероятности, используя формулу Бернулли

, так как всего РЛС три (n=3), вероятность c помощью РЛС обнаружить объект, известна p=0,2. Соответственно вероятность не обнаружить с помощью РЛС объект равна q=1-p=1-0,2=0,8.

Таким образом, получим:

 

 

 

 

Контроль:

 

 – верно.

Построим теперь ряд распределения нашей СВ Х:

 

Найдем функцию распределения  то есть

При

При

При

При

При

 

 

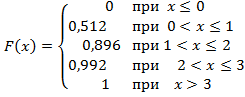
Найдем теперь числовые характеристики  нашей СВ X:

1) математическое ожидание ;

2) дисперсию ;

3) среднее квадратичное отклонение .

 

 

Задания для самостоятельной работы:

 

Вариант №1   Задание №1. Найти вероятность сборки букета из 10 роз и 5 лилий, если всего у флориста имеется 23 цветка, из которых 14 роз и 9 лилий.   Задание №2. В автосалоне имеется 30 отечественных и 23 иностранных автомобиля. Вероятность брака в отечественных авто составляет 0,5%, а в иностранных авто – 0,4%. Найти вероятность того, что: а) купленный наугад автомобиль будет бракован; б) наугад купленный бракованный автомобиль является иномаркой.   Задание №3. На контроль качества медицинских препаратов поступила партия из 6 штук. Вероятность того, что препарат окажется некачественным, равна 0,15. Построить ряд распределения, найти функцию распределения, математическое ожидание, дисперсию и среднее квадратичное отклонение числа некачественным медицинских препаратов.

Вариант №2   Задание №1. Вероятность попадания в цель при одном выстреле для первого стрелка равна 0,75, для второго – 0,8, для третьего – 0,85, для четвертого – 0,9 соответственно. Произведено по одному выстрелу каждым стрелком. Найти вероятность тог, что в мишени менее двух пробоин.   Задание №2. На заводе, производящем замки, первый цех производит 20%, второй – 35%, третий 45% всех замков. Брак составляет соответственно 4%, 2% и 1% продукции соответственно. Найти вероятность того, что: а) наудачу выбранный замок будет стандартным; б) наудачу выбранный стандартный замок произведен либо 2-ым, либо 3-им цехами.   Задание №3. Для расчистки улиц от снега имеется 7 тракторов, причем вероятность поломки одного трактора равна 0,25. Построить ряд распределения, найти функцию распределения, математическое ожидание, дисперсию и среднее квадратичное отклонение числа исправных тракторов.

 

Контрольные вопросы (ответьте письменно):

1.                  Запишите формулу классической вероятности.

2.                  Запишите формулу геометрической вероятности.

3.                  Запишите формулу статистической вероятности.

4.                  Запишите формулу полной вероятности.

5.                  Запишите формулу Байеса.

6.                  Запишите формулу Бернулли.

7.                  Запишите определение случайной величины.

8.                  Запишите определение ряда распределения СВ.

9.                  Запишите определение функции распределения СВ.

 

10.