Фигурные числа

ФИГУРНЫЕ ЧИСЛА

Целое число — основное понятие ариф­метики. Изучение его свойств, в особенности таких, которые относятся к установлению законов делимости, законов распределения простых чисел и следования их друг за дру­гом, привлекало к себе внимание очень многих математиков уже в очень отдаленные от нас времена.

Известно, какое значение придавали изу­чению свойств целых чисел Пифагор и его ученики, выставившие тезис о том, что «числа правят миром».

Пифагорейцы, а также и греческие мате­матики более поздних веков (Евклид, Эра­тосфен) очень интересовались так называе­мыми «совершенными» числам, т. е. такими, сумма всех настоящих делителей которых равна рассматриваемому числу (например 28 = 1 + 2 + 4 + 7 + 14), или числами «дружественными», т е. такими парами чисел, у которых сумма настоящих делителей каждого из них равна другому. Совершенными и дружественными числами интересовались Фермат, Эйлер.

Благодаря Фермату же получили извест­ность и «многоугольные», или «фигурные», числа. Рассмотрим некоторые свойства этих последних. Их характер и происхождение термина можно выяснить следующим образом. Представим себе, что на продолжении сто­роны правильного n-угольника, равной еди­нице длины, строятся один за другим подоб­ные многоугольники, с центром подобия в общей для всех вершине и двумя общими сторонами, выходящими из взятой вершины (см. чертеж для случая п— 4); длины сторон должны возрастать при этом на 1 при переводе одного многоугольника к следую­щему. Будем нумеровать по порядку, начи­ная с общей вершины, все точки сторон многоугольников, отстоящие друг от друга на 1, так, чтобы, обходя периметры 1-го 2-го, З-го и т. д. многоугольников, в направлении вращения часовой стрелки, занумеровать каждую такую точку только один раз. Тогда на той, общей всем многоугольникам стороне, на которой окажется точка с номе ром п, расположатся последовательно «-уголь ные числа различных порядков, начиная с 1-го: 1п, 3n - 3, 6п - 8. . . и т. д.

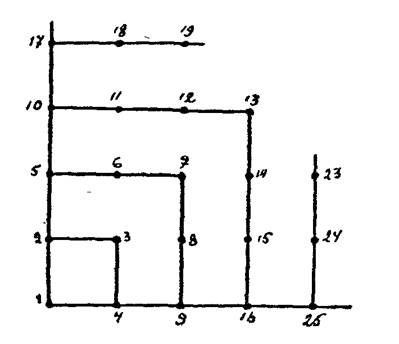
Не трудно видеть, что всякое n-угольное число m-го порядка есть, таким образом, сумма т первых членов арифметической прогрессии, первый член которой всегда = 1, а разность равна п — 2 Таким образом, тре­угольные, квадратные, пятиугольные и т. д. числа /га-го порядка суть суммы т первых чисел прогрессий.

1,  2, 3, 4, …, т

1, 3, 5, 7, ... , 2т — 1

1, 4, 7, 10, ... , .3m —2

Поэтому общее выражение для n-угольного числа  m-го порядка будет:

Приняв выражение (1) как определение n-угольного числа m-го порядка, будем счи­тать, что числа п и т в (1) могут прини­мать следующие значения:

п = 3, 4, 5, ... и т. д.

m  = 0, 1, 2, 3, 4, ... и т. д.

В течение почти двух веков (XVII — XIX) многоугольные числа привлекали к себе внимание математиков, пытавшихся доказать следующую теорему, высказанную, но не доказанную Ферматом:

«Всякое целое положительное число может быть представлено в виде суммы трех треугольных, четырех четырехугольных, пяти пятиугольных и т. д. чисел».

Впервые эту теорему доказал Коши, видоизменив ее условие следующим обра­зом:

«Всякое целое положительное число может быть представлено в виде суммы п п-угольных чисел, из кото­рых по крайней мере п — 4 числа суть 0 или 1».

Скачано с www.znanio.ru