Финансовая математика в ЕГЭ

Финансовые задачи
 в профильном ЕГЭ по математике

 

МБОУ «Средняя школа №3 имени Ленинского комсомола»

Учитель высшей кв.категории математики

Никитина Елена Анатольевна

 

 

Экономическую задачу ввели в экзамен ЕГЭ «Профиль по математике» только с 2015 года. Она стала называться заданием номер 17 и по своей сложности находится на одном уровне с заданиями на параметры и теорию чисел. В экзаменационных заданиях по математике (профильный уровень) с 2022 года  задача с экономическим содержанием (финансовая математика) присутствует во 2 части работы и, сейчас содержится под №15. Она относится к повышенному уровню сложности и оценивается максимально в 

2 балла.

Участники экзамена, которые не смогли выполнить данное задание, делятся на две группы: те, кто не смог составить математическую модель решения (или составил её неверно), и те, кто допустил ошибки (как правило, вычислительные) при решении полученного уравнения.

Следует отметить резкое снижение за последние годы доли участников экзамена, которые допустили ошибки при составлении математической модели. Это является следствием в том числе резкого усиления внимания к практико-ориентированным заданиям в школьном курсе. При этом рост сформированности культуры решения уравнений, безошибочного выполнения математических действий, несколько отстаёт, так как основы этого закладываются в 1–6 классах. Соответственно, заметное число участников ЕГЭ, которые, приступив к выполнению задания, не смогли решить его, верно составило уравнение, но из-за вычислительных оши-

бок не смогло получить правильный ответ.

 

Для успешного решения подобных задач требуется не только владеть определенным математическим инструментарием, но и уметь строить простейшие математические модели по заданным условиям.

В отличие от других экзаменационных заданий, «экономические» задачи не отличаются большим разнообразием и встречаются лишь нескольких типов. В данной методической разработке разобраны все типы задач №15, которые предлагаются разработчиками ЕГЭ для подготовки к выпускным экзаменам .

 

Условно задачи финансовой на три большие группы:

·         банковские задачи, 

·         на ценные бумаги,

·         задачи на оптимальный выбор. 

Главная трудность — школьник плохо понимает условие, ведь с кредитами и вкладами он пока не сталкивался.

·         Как работает процент по кредиту?

·         На какую сумму начисляется?

·         Из каких частей состоит платеж?

·         Как уменьшается долг?

На все эти вопросы придется ответить. Это отличная возможность показать пользу уроков математики, ведь 15-ый номер — едва ли не самая прикладная задача за весь школьный курс! 

На различных сайтах и в математической литературе можно найти решения таких задач, но зачастую либо они содержат много лишней информации, либо они решены непонятным способом. При решении задач  использую  табличный метод, так как считаю его самым наглядным и простым.

 

Решение финансовых задач основывается на использовании различных математических моделей: уравнений, неравенств, их систем с привлечением процентов, арифметической и геометрической прогрессий и производной. Приведу основные определения, понятия, таблицы и формулы.

 

Определение: один процент – это одна сотая доля. Чтобы найти данное число процентов от числа, нужно проценты записать десятичной дробью, а затем число умножить на эту десятичную дробь.

Пример: 5% от 80 это будет 0,05

r% от 14 это будет 0,01r =

При решении задач необходимо понимать механизм начисления процентов по вкладам или кредитам. Например, если банк выдаёт кредит на сумму S  клиенту, то через год клиент должен банку не только сумму кредита, но и некий процент r .Возникает необходимость введения нового коэффициента к, к = 1+0,01r =1 + .С учётом этого , долг клиента банку через год составит:

S + r% от S  , т.е  S + 0,01r = S (1 + 0,01r)= S(1 + = кS

Платежи.

В задачах по теме «Кредит» используют о три основных вида платежа:

1.      Фиксированные платежи(платежи, которые чётко оговариваются в условии задачи)

2.      Аннуитетные платежи(постоянные ежемесячные или ежегодные платежи, которые не меняются на протяжении всего периода кредитования)

3.      Дифференцируемые платежи(ежемесячные или ежегодные платежи, уменьшающиеся к концу срока кредитования и обеспечивающие уменьшение суммы долга на одну и ту же величину)

 

При решении задач, связанных с аннуитетными  платежами мне было очень удобно заполнять следующую таблицу:

S – сумма кредита

 r% - годовые (ежемесячные) проценты

к =1+0,01r – коэффициент

х – ежегодная (ежемесячная) выплата

Год	Долг с %	Выплата	Долг после выплаты
0			S
1	Sк	x	Sк-x
2	(Sк-x)к=Sк2-xк	x	Sк2-xк-x
3	(Sк2-xк-x)к=Sк3-xк2-xк	x	Sк3-xк2-xк-x
4	(Sк3-кх2-кx-x)b= Sк4-xк3-xк2-xк	x	Sк4-xк3-xк2-xк-x
5	(Sк4-xк3-xк2-xк-x)к =Sк5-xк4-xк3-xк2-xк	x	Sк5-xк4-xк3-xк2-xк-x
…	И так далее		…
n	Sкn-xкn-1-xкn-2-…-xк2-xк	x	0

 

При решении задач, связанных с дифференцированными платежами я использовала следующую таблицу:

 

Месяц	Долг с %	Выплата	Долг после выплаты
0			S
1	Sк	Sк
2
…	И т.д
n-1
n			0

Или

Месяц	Долг с %	Выплата	Долг после выплаты
0			S
1	Sк	S
2
n-1
n		+	0

 

При решении задач по теме «Вклады»:

 

Год	Вклад с %
0
1	Sк
2	Sк2
	….
n	Sкn

 

При решении задач, в которых осуществлялись какие-либо действия (пополнение или снятие денег с вклада):

х – действие

Год	Вкладс %	Действие	Вклад после действия.
0			S
1 год	Sк	+х	Sк+x
2 год	к(Sb+к)= Sк2+кb	+х	Sк2+xк+x
3 год	к (Sк2+xк+x)=Sк3_+хк2+xк	Снял вклад

 

 

Арифметическая и геометрическая прогрессии.

Арифметическая прогрессия

Определение. Последовательность чисел, в которой каждое следующее отличается от предыдущего ровно на одну и ту же величину, называется арифметической прогрессией.

Любой член арифметической прогрессии вычисляется по формуле:

 =  + (n-1)d

Формула суммы n-первых членов арифметической прогрессии

S_n=

S_n=

 

С учётом этой формулы:(n-1) + (n-2) +…+3+2+1 = =

 =  =

==

Геометрическая прогрессия

Определение. Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.

Любой член геометрической прогрессии вычисляется по формуле:

b_n =b₁· q^n-1

Формула суммы n-первых членов геометрической прогрессии

S_n=

Из этой формулы следует: b^n-1+b^n-2 +…+b²+b+1=

 Производная.

Достаточные признаки возрастания и убывания функции:

Если производная данной функции положительна для всех значений х в интервале (а; в),т.е.f'(x) > 0,то функция в этом интервале возрастает. 
Если производная данной функции отрицательна для всех значений х в интервале(а; в), т.е.f'(x) < 0, то функция в этом интервале убывает

Порядок нахождения промежутков монотонности:

 Найти область определения функции.

1.Найтипроизводную функции.

2.Найти критические точки (точки, в которых производная не существует) и стационарные (точки, в которых производная равна нулю). Исследовать знакпроизводной в промежутках, на которые найденные точки делят область определения функции.

 Достаточное условие существования максимума состоит в смене знака производной при переходе через критическую точку с "+" на "-", а для минимума с "-" на "+". Если при переходе через критическую точку смены знака производной не происходит, то в данной точке экстремума нет

Экономическая задача пробного ЕГЭ по математике (январь 2022)

1.В июле планируется взять кредит в банке на сумму 4 млн. рублей на некоторый срок. Условия его возврата таковы:

— каждый январь долг возрастает на 15% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга;

— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.

На какой минимальный срок следует брать кредит, чтобы наибольший годовой платёж по кредиту не превысил 1,25 млн. руб.?

S= 4 млн. рублей на n лет.

r = 15%   к = 1,15

х_мин 1,25 млн.руб.

Год	Долг с %	Выплата	Долг после выплаты
0			S
1	1,15S	S
2
3
И т.д
n-1
n		+	0

 

Наибольший годовой платеж – в 1 первый год.

 S≤1,25

 · 4 ≤1,25

n≠0 

)

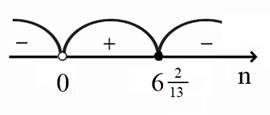
Учитываем n

№2.

15-го декабря планируется взять кредит в банке на 600 000 рублей на

26 месяцев. Условия его возврата таковы:

− 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца;

− cо 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

− 15-го числа с 1 по 25 месяц долг должен уменьшаться на одну и ту же сумму;

− 15-го числа 26 месяца долг должен быть погашен.

Сколько тысяч рублей составляет долг на 15 число 25 месяца, если всего было выплачено 691 тысяч рублей?

S=600 тыс. рублей r = 1%

n=26 мес.

М=691 тыс. руб.

Пусть х- тысяч рублей составляет долг на 15 число 25 месяца

 

 

 

 

 

 

Год	Долг с %	Выплата	Долг после выплаты
0			S
1	1,01S	+0,01S
2	1,01	+ 0,01
3	1,01	+0,01
И т.д
25	1,01	+0,01	х
26	1,01x	1,01x	0

 

A – уменьшение долга до 25 месяца.

Арифметическая прогрессия

S	S-A	S-2A	…..	х	0
а26	а25	а24		а1

 =  + (n-1)d

  а₂₆ = a₁+ 25d

 S = x + 25A

A =

Долги после выплаты:

1 месяц.

S-A = S - =

2 месяц.

 -  =

3 месяц.

-

И так далее.

Выплаты

1 месяц.

1,01S - = S +0,01S -  = S - +0,01S =+0,01S

2 месяц.

1,01 =  + 0,01=  + 0,01=

=+ 0,01

И так далее.

Выплаты за 25 месяцев:

+0,01S + + 0,01 + +0,01+…++0,01 =

= 25· +0,01  + 0,01 + +0,01+…+0,01 =

= S – x +( 25S +24S+x +23S+2x+… + S + 24x) =

=S – x +( (25S +24S +23S+… + S ) + ( x+2x +….+24x))

                         S_n=

1)  25S +24S +23S+… + S = 325S

2)  x+2x +….+24x =

S – x +(325S +300x)=S-x +0,13S +0,12x= 1,13S – 0,88x

Все выплаты:

1,13S – 0,88x +1,01x = 691

1,13·600+0,13х=691

0,13х=691-678

0,13х=13

х=13:0,13

х=100

Ответ: 100 тыс.рублей.

№3. Вклад в размере 10 млн. рублей планируется открыть на четыре года. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего года и четвёртого годов вклад ежегодно пополняется на одну и ту же фиксированную сумму, равную целому числу миллионов рублей. Найдите наименьший возможный размер такой суммы, при котором через четыре года вклад станет не меньше 30 млн. рублей.

S=10 млн. рублей

n=4года

к = 10 % - в конце года

3,4 год  + х млн. рублей (целое)

Наименьшее х-?

Через 4 года  вклад не меньше 30 млн. рублей.

 

 

Год	В начале года	Действие	Вклад   в конце года
1	S		1,1S
2	1,1S		1,21S
3	1,21S	+ х	1,31S+1,1x
3	1,31S+1,1x	+x	14,641+2,31 x

 

14,641+2,31 x ≥ 30

2,31х≥30-14,641

2,31х≥15,359

х  ≥

х ≥

7-наименьшее целое решение неравенства, значит , искомая сумма 7 млн.руб.

Ответ: 7 млн.руб.

№4. Необходимо произвести отделку здания, имеющего форму прямоугольного параллелепипеда объемом 432 м³. Отделка стены здания, примыкающей к внутреннему строению, обходится в 1000 руб. за квадратный метр. Отделка трех фасадных стен обходится в 2000 руб. за квадратный метр. А заливка крыши, форма которой является квадратом, обходится в 7000 руб. за квадратный метр. Найдите размеры здания, отделочные работы которого при данных условиях являются наименьшими по стоимости.

V = 432 м³

1 стена ( примыкающая) -1 тыс. руб. за квадратный метр

2 стена (фасад) – 3 шт. - в 2 тыс.  руб. за квадратный метр

Крыша квадратная  -7 тыс. руб. за квадратный метр

Размер здания- ? себестоимость- наименьшая.

По условию форма крыши является квадратом, значит, длина и ширина здания равны.

Пусть длина и ширина здания равны x м , x> 0,

тогда высота здания равна  м.

Стоимость отделки здания в тысячах  рублей равна:

Крыша  7·x²

Примыкающая стена  1·x·  

Три фасадные стены  3·2·x·

f(x) =  7·x² + 1·x·  + 3·2·x·

f(x) =  7(х² +

Найдем производную функции:

f ˊ (x) = 7(2 x -  ) = 14(x  -  )= 14·

f ˊ (x) = 0, х> 0

14·

x=6

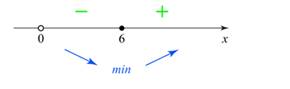
Точка минимума  x = 6  является единственной точкой экстремума непрерывной на луче (0; +∞) функции  f(x) =  7(х² +

поэтому в данной точке эта функция принимает наименьшее значение.

Значит, длина и ширина здания равны 6 м,

а высота здания равна 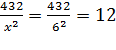 м.

 

Ответ: 6 м, 6 м, 12 м.

 

 

Литература

1)Федеральная служба   по надзору в сфере образования и науки

ФГБНУ « Ф е д е р а л ь н ы й и н с т и т у т п е д а г о г и ч е с к и х и з м е р е н и й »

И.В. Ященко, И.Р. Высоцкий, А.В. Семенов МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ 2021 года

по МАТЕМАТИКЕ , Москва, 2021

2) ЕГЭ 2022 под редакцией А. Л. Семенова, И.В. Ященко

3)Открытый банк заданий ЕГЭ http://os.fipi.ru/tasks/2/a

4)      Сайт «Решу ЕГЭ»

5) Сайт «Алекс Ларин»

 

 

Скачано с www.znanio.ru