I Паспорт фонда оценочных средств

1.1 Область применения

Фонд оценочных средств предназначен для контроля и оценки образовательных достижений обучающихся, освоивших программу учебной дисциплины «Элементы высшей математики»среднего профессионального образования в пределах ОПОП СПО.

Фонд оценочных средств разработан в соответствии с требованиями ФГОС нового поколения специальности СПО 09.02.07 Информационные системы и программирование

и рабочей программой учебной дисциплины «Элементы высшей математики»

Учебная дисциплина, в соответствии с учебным планом, изучается на втором курсе и завершается экзаменом по изученным темам.

Фонд оценочных средств, предназначен для проверки результатов освоения дисциплины «Элементы высшей математики»в части овладения следующими знаниями, умениями:

уметь:

- выполнять операции над матрицами

- решать системы линейных уравнений;

- решать задачи, используя уравнения прямых и кривых второго порядка на плоскости;

- применять методы дифференциального и интегрального исчисления;

- решать дифференциальные уравнения;

- пользоваться понятиями теории комплексных чисел;

знать:

- основы математического анализа, линейной и аналитической геометрии;

- основы дифференциального и интегрального исчисления

- основы теории комплексных чисел.

2 Процедура и методика контроля успеваемости и оценивания результатов освоения программы дисциплины

2.1 Перечень компетенций, формируемых в процессе изучения дисциплины

- OK 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.

- ОК 2. Организовывать собственную деятельность, определять методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

- ОКЗ. Решать проблемы, оценивать риски и принимать решения в нестандартных ситуациях.

- ОК 4. Осуществлять поиск, анализ и оценку информации, необходимой для постановки и решения профессиональных задач, профессионального и личностного развития.

- ОК 5. Использовать информационно-коммуникационные технологии для совершенствования профессиональной деятельности.

- ОК 6. Работать в коллективе и команде, обеспечивать ее сплочение, эффективно общаться с коллегами, руководством, потребителями.

- ОК 7. Ставить цели, мотивировать деятельность подчиненных, организовывать и контролировать их работу с принятием на себя ответственности за результат выполнения заданий.

- ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.

- OK 9. Быть готовым к смене технологий в профессиональной деятельности.

Программист должен обладать профессиональными компетенциями, соответствующими видам деятельности:

ПК 1.1 Выполнять проектирование кабельной структуры компьютерной сети

- ПК 1.2 Осуществлять выбор технологии, инструментальных средств и средств вычислительной техники при организации процесса разработки и исследования объектов профессиональной деятельности.

- ПК 1.4. Принимать участие в приемо-сдаточных испытаниях компьютерных сетей и сетевого оборудования различного уровня и в оценке качества и экономической эффективности сетевой топологии.

- ПК 2.3 Обеспечивать сбор данных для анализа использования и функционирования программно - технических средств компьютерных сетей.

Оценивание результатов обучения студентов по дисциплине «Элементы высшей математики» осуществляется по регламенту текущего контроля и промежуточной аттестации.

Текущий контроль в семестре проводится с целью обеспечения своевременной обратной связи, для коррекции обучения, активизации самостоятельной работы студентов. Текущий контроль осуществляется два раза в семестр по календарному графику учебного процесса в рамках проведения контрольных работ.

Формы текущего контроля знаний:

- устный опрос;

- письменный опрос;

- тестирование;

- выполнение и защита практических работ; -выполнение практических заданий.

Проработка конспекта лекций и учебной литературы осуществляется студентами в течение всего семестра, после изучения новой темы.

3 Комплект материалов для оценки освоенных умений и усвоенных знаний по дисциплине

Комплект контрольно - оценочных средств, включает в себя педагогические контрольноизмерительные материалы, предназначенные для определения соответствия (или несоответствия) индивидуальных образовательных достижений основным показателям результатов подготовки.

3.1 Текущий контроль

Основы математического анализа.

Теория пределов. Непрерывность.

Вопросы для устного опроса по теме.

1. Дайте определение предела в точке.

2. Объясните раскрытие неопределенности .

3. Дайте определение предела функции на бесконечности. Объясните основной метод раскрытия неопределенности .

4. Сформулируйте теоремы о пределах.

5. Сформулируйте и напишите первый и второй замечательные пределы.

Тестовое задание

Текст задания

Вариант 1

1. Чему равен предел функции ?

а) 9; б) 10; в) 8.

2. Чему равен предел функции ?

а)0; б) 0,167; в) .

3. Чему равен предел функции

а) ; б) 3; в) 1.

4. Какому пределу функции равен данный предел ?

а) ; б) ; в) .

5. К какому значению стремится x , если предел =3?

а) 0; б) ; в) 1.

Вариант 2

1. Чему равен предел функции ?

а) 11; б) 101; в) 1.

2. Чему равен предел функции ?

а)0; б) 0,167; в) .

3. Чему равен предел функции

а) ; б) 4; в) 0,25.

4. Какому пределу функции равен данный предел ?

а) ; б) ; в) .

5. К какому значению стремится x , если предел =4?

а) 0; б) ; в) 1.

Вариант 3

1. Чему равен предел функции ?

а) 11; б) 89; в) 1.

2. Чему равен предел функции ?

а)0; б) ; в)0,1.

3. Чему равен предел функции

а) ; б) 7; в) 0,25.

4. Какому пределу функции равен данный предел ?

а) ; б) ; в) .

5. К какому значению стремится x , если предел =7?

а) 0; б) ; в) 1.

Вариант 4

1. Чему равен предел функции ?

а) 11; б)989; в) 1.

2. Чему равен предел функции ?

а)0; б) ; в)

3. Чему равен предел функции

а) ; б) 9; в) 0,25.

4. Какому пределу функции равен данный предел ?

а) ; б) ; в) .

5. К какому значению стремится x , если предел =9?

а) 0; б) ; в) 1.

Расчетное задание

Текст задания

Вариант 1

Исследовать функцию на непрерывность в точке .

Вариант 2

Исследовать функцию на непрерывность в точке .

Вопросы для устного опроса по теме.

1. Что называется приращением независимой переменной и приращением функции?

2. Дайте определение непрерывной функции. Какими свойствами на отрезке она обладает?

3. Что характеризует скорость изменения функции относительно изменения аргумента? Дайте определение производной.

4. Какая функция называется дифференцируемой в точке и на отрезке? Сформулируйте зависимость между непрерывностью и дифференцируемостью функции.

5. Из каких операций складывается общее правило нахождения производной данной функции? Как вычислить частное значение производной?

6. Можно ли вычислить производную любой функции, пользуясь определением производной?

7. Выпишите в таблицу основные правила и формулы дифференцирования функций.

8. Повторите определение сложной функции. Как найти ее производную?

9. Каков геометрический смысл производной? Как геометрически определить значение производной в точке?

10. В чем заключается механический смысл производной?

11. Что называется производной второго порядка и, каков ее механический смысл?

12. Что называется дифференциалом функции, чему он равен, как обозначается и каков его геометрический смысл?

13. Повторите определения возрастающей и убывающей функций. В чем заключается признак возрастания и убывания функций?

14. В чем заключаются необходимый и достаточный признаки существования экстремума? Перечислите порядок операций для отыскания максимума и минимума функции с помощью первой производной.

15. В чем различие между нахождением максимума и минимума функции и нахождением ее наибольшего и наименьшего значений?

16. Как пишется наибольшее и наименьшее значения функции на данном отрезке?

17. Как определяются геометрически и по знаку второй производной выпуклость и вогнутость кривой?

18. Что называется точкой перегиба и каковы необходимый и достаточный признаки ее существования? Сформулируйте правило нахождения точки перегиба.

19. Какой схемой рекомендуется пользоваться при построении графика функции?

Текст задания

Сформулировать правила дифференцирования и записать производные основных элементарных функций:

1^о.		8^о.
2^о.	В частности,	9^о.
		10^о.
		11^о.
		12^о.
		13^о.
		ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
		14^о.
3^о.		15^о.
4^о.	В частности,	16^о.
4^о.	В частности,	17^о.
5^о.	В частности,	18^о.	В частности,
6^о.		ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ
7^о.		19^о.

Расчетное задание

Текст задания

Вариант 1

1. Найти производную функции .

2. Найти производную третьего порядка функции .

3. Написать уравнение касательной к графику функции в точке с абсциссой , .

4. Материальная точка движется по закону . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)

Вариант 2

1. Найти производную функции .

2. Найти производную третьего порядка функции .

3. Написать уравнение касательной к графику функции в точке с абсциссой , .

Вариант 3

1. Найти производную функции .

2. Найти производную третьего порядка функции .

3. Написать уравнение касательной к графику функции в точке с абсциссой , .

Вариант 4

1. Найти производную функции .

2. Найти производную третьего порядка функции .

3. Написать уравнение касательной к графику функции в точке с абсциссой , .

Расчетное задание

Текст задания

Исследовать функцию и построить ее график.

Вариант 1

Вариант 2

Вариант 3

Вариант 4

Интегральное исчисление функции одной действительной переменной.

Вопросы для устного опроса по теме.

1. Что является основной задачей интегрального исчисления?

2. Какая функция называется первообразной для заданной функции?

3. Почему при интегрировании функций появляется произвольная постоянная?

4. Почему одна функция имеет целую совокупность первообразных?

5. Как записать всю совокупность первообразных функций?

6. Что называется неопределенным интегралом?

7. Почему интеграл называется неопределенным?

8. Что означает постоянная С в определении неопределенного интеграла?

9. В чем заключается правило интегрирования выражения, содержащего постоянный множитель?

10. В чем заключается правило интегрирования алгебраической суммы функций?

11. Чему равен интеграл от дифференциала некоторой функции?

12. Напишите основные формулы интегрирования.

13. Как проверить результата интегрирования?

14. В чем состоит геометрический смысл неопределенного интеграла?

15. Что такое интегральные кривые? Как они расположены друг относительно друга? Могут ли они пересекаться?

16. Что такое определенный интеграл?

17. Сформулируйте основные свойства определенного интеграла.

18. В чем заключается геометрический смысл определенного интеграла?

19. Может ли площадь криволинейной трапеции быть равна отрицательной величине, нулю и почему?

20. Какие интегралы называются несобственными?

Расчетное задание

Текст задания

Вариант 1

Найти неопределенные интегралы методом непосредственного интегрирования (для № 1-5).

1. .

2. .

3. .

4. .

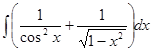5. .

Найти неопределенные интегралы методом подстановки (для № 6-8).

6. .

7. .

8. .

9. Найти неопределенный интеграл методом интегрирования по частям: .

Вариант 2

Найтинеопределенные интегралы методом непосредственного интегрирования (для № 1-5).

1. .

2. .

3. .

4. .

5. .

Найти неопределенные интегралы методом подстановки (для № 6-8).

6. .

7. .

8. .

9. Найти неопределенный интеграл методом интегрирования по частям: .

Самостоятельная работа

Текст задания

Записать табличные интегралы:

1^о.

2^о.

В частности,

3^о.

4^о.

В частности,

5^о.

6^о.

7^о.

8^о.

9^о.

В частности,

10^о.

В частности,

Расчетное задание

Текст задания

Вариант 1

1. Вычислить определенный интеграл: .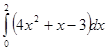

2. Вычислить определенный интеграл методом подстановки: .

3. Вычислить, предварительно сделав рисунок, площадь фигуры, ограниченной линиями: .

4. Найти объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями:.

5. Скорость движения точки изменяется по закону (м/с). Найти путь S, пройденный точкой за 10 с от начала движения.

Вариант 2

1. Вычислить определенный интеграл: .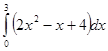

2. Вычислить определенный интеграл методом подстановки: .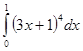

3. Вычислить, предварительно сделав рисунок, площадь фигуры, ограниченной линиями: .

5. Скорость движения точки изменяется по закону (м/с). Найти путь S, пройденный точкой за четвертую секунду.

Основы теории вероятностей и математической статистики.

Вопросы для устного опроса по теме.

1. Что называется n-факториалом?

2. Перечислите основные задачи комбинаторики.

3. Что называется перестановками?

4. Запишите формулу для числа перестановок из m элементов.

5. Что называется размещениями?

6. Запишите формулу числа размещений из m элементов по n.

7. Что называется сочетаниями?

8. Запишите формулу числа сочетаний из m элементов по n.

9. Какие события называются достоверными? Приведите примеры.

10. Какие события называются невозможными? Приведите примеры.

11. Что называется вероятностью события?

12. Какие события называются несовместными? Приведите примеры.

13. Чему равна сумма несовместных событий?

14. Какие события называются противоположными? Приведите примеры.

15. Как формулируется теорема сложения вероятностей?

16. Чему равна сумма вероятностей противоположных событий?

17. Как формулируется теорема умножения вероятностей?

18. Какая величина называется случайной?

19. Какая случайная величина называется дискретной?

20. Что называется законом распределения случайной величины?

21. Какой закон распределения называется биномиальным?

22. Что называется математическим ожиданием дискретной случайной величины?

23. Что называется дисперсией случайной величины?

24. Что понимается под законом больших чисел?

Численные методы.

Приближенные вычисления.

Приближенное вычисление определенных интегралов.

Вопросы для устного опроса по теме.

1. Какое число называется приближенным?

2. Что называется истинной погрешностью и истинной абсолютной погрешностью?

3. Что называется границей абсолютной погрешности?

4. Какие цифры приближенного числа называются верными?

5. Какие цифры приближенного числа называются сомнительными?

6. Сформулируйте правило записи приближенных чисел. Приведите примеры.

7. Как округляются приближенные числа?

8. Что называется границей абсолютной погрешности приближенного числа?

9. Что называется границей относительной погрешности приближенного числа?

10. Перечислите правила действий с приближенными числами. Приведите примеры.

11. Формулы прямоугольников.

12. Формула трапеций.

13. Способы вычисления абсолютной погрешности при численном интегрировании.

14. Формулы приближенного дифференцирования, основанные на интерполяционных формулах Ньютона.

15. Способы вычисления погрешности в определении производной.

16.

Приближенное решение дифференциальных уравнений.

Вопросы для устного опроса по теме.

1. Метод Эйлера и нахождение значения функции с использованием метода Эйлера.

2. Понятие интегральной кривой.

3. Построение интегральной кривой.

Теоретические вопросы для проведения экзамена

Основные понятия матриц. Свойства матриц.
Действия над матрицами. Элементарные преобразования.
Произведение матриц.
Определители матриц и их свойства.
Способы вычисления определителей.
Системы линейных уравнений (основные понятия).
Решение систем линейных уравнений способом подстановки, графическим способом, способом алгебраического сложения.
Формулы Крамера.
Метод Гаусса.
Функции одной независимой переменной, их графики. Приращение функции.
Предел числовой последовательности.
Предел функции в точке. Непрерывность функции.
Производная функции в точке, ее физический и геометрический смысл.
Правила и формулы дифференцирования.
Производная сложной функции. Дифференциал функции.
Производные высших порядков. Экстремумы функций.
Неопределенный интеграл. Непосредственное интегрирование.
Метод замены переменной. Метод интегрирования по частям.
Определенный интеграл, понятие определенного интеграла как предела интегральной суммы. Формула Ньютона-Лейбница.
Вычисление определенного интеграла различными методами.
Геометрический смысл определенного интеграла.
Задачи, приводящие к дифференциальным уравнениям. Задача Коши.
Дифференциальные уравнения с разделяющимися переменными. Общие и частные решения.
Однородные дифференциальные уравнения первого порядка.
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Числовые ряды. Необходимый признак сходимости ряда.
Достаточные признаки сходимости рядов с положительными членами.
Знакопеременные и знакочередующиеся ряды. Абсолютная и условная сходимость. Признак Лейбница для знакочередующихся рядов.
Степенные ряды. Радиус сходимости степенного ряда. Разложение элементарных функций в степенные ряды.
Комплексные числа и действия над ними. Геометрическая интерпретация комплексных чисел.
Тригонометрическая и показательная формы записи комплексного числа. Переход от одной формы записи в другую.
Действия над комплексными числами в тригонометрической и показательной формах. Решение уравнений с отрицательным дискриминантом.
Понятие события и вероятности события. Достоверные и невозможные события. Классическое определение вероятности.
Теорема сложения вероятностей. Теорема умножения вероятностей.
Случайная величина. Дискретная и непрерывная случайные величины. Закон распределения дискретной случайной величины.
Математическое ожидание дискретной случайной величины. Дисперсия случайной величины. Среднее квадратичное случайной величины

Типовые задания для проведения экзамена.

1. Вычислить определитель.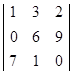

2. Даны матрицы,. Найти матрицу 2А-3В

3. Перемножить матрицы 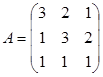и .

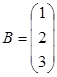4. Перемножить матрицыи .

5. Решить систему по формулам Крамера

6. Решить систему методом Гаусса

7. Записать число z=3-i, в тригонометрической и показательной форме.

8. Записать число в алгебраической форме.

9. Вычислить (4-2i)(1+2i).

10. Вычислить .

11. Найти произведение z₁∙z₂, если ,.

12. Выполнить деление чисел , если ,

13. Найти z³, если .

14. Извлечь корень , если .

15. Вычислить предел .

16. Вычислить предел .

17. Вычислить предел .

18. Найти производную функции y=cosx³

19. Найти производную функции y=2x+3lnx.

20. Найти производную функции y=3x-4.

21. Найти производную функции y=ln5-4x.

22. Найти производную функции y=e^x(x²-2).

23. Найти производную функции y=e^tqx

24. Найти дифференциал функции y=2x-sin2x.

25. Найти дифференциал функции .

26. Найти производную второго порядка функции y=e^xcosx

27. Найти производную второго порядка функции y=x²-2xlnx

28. Найти точки максимума (минимума) функции y=x³-12x+1

29. Найти .

30. Найти .

31. Найти .

32. Найти .

33. Найти .

34. Найти .

35. Вычислить .

36. Вычислить .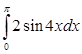

37. Вычислить .

38. Вычислить .

39. Вычислить .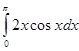

40. Вычислить площадь фигуры, ограниченную линиями y=4- x²и y=0.

41. Вычислить площадь фигуры, ограниченную линиями y=x³ ,y=8 и y=0.

42. Определить объем тела, образованного вращением фигуры, ограниченной линиями , x=1, x=4 вокруг оси OX.

43. Определить объем тела, образованного вращением фигуры, ограниченной линиями y=x², x=0,x=2 вокруг оси OX.

44. Определить объем тела, образованного вращением фигуры, ограниченной линиями y=2x-1, x=1,x=3 вокруг оси OX.

45. По прогнозу метеорологов вероятность того, что пойдет дождь, равна 0,4, будет ветер – 0,7, будет ветер с дождем – 0,2. Какова вероятность того, что будет дождь или ветер?

46. Совет директоров состоит из трех бухгалтеров, трех менеджеров и двух инженеров. Планируется создать подкомитет из его членов. Какова вероятность того, что все трое в этом подкомитете будут бухгалтеры?

47. Рабочий обслуживает три станка. Вероятность того, что в течение часа станок не требует внимания рабочего, равна для первого станка 0,9, для второго – 0,8, для третьего -0,85. Найти вероятность того, что в течение часа хотя бы один станок потребует внимания рабочего?

48. Случайная величина X распределена по закону

xi	0,5	1	1,5	2
pi	0,2	0,3	0,4	0,1

Найти математическое ожидание случайной величины Х.

49. Случайная величина X распределена по закону

xi	1	3	4
pi	0,2	0, 5	0,7

Найти дисперсию случайной величины Х.

50. Для выборки, представленной статистическим рядом

xi	10	15	20	25
ni	4	6	4	2

определить среднее значение.

51. Для выборки, представленной статистическим рядом

xi	15	16	18	19
ni	1	4	5	2

определить дисперсию.

52. В магазин поступило 30 новых телевизоров, среди которых 5 имеют скрытые дефекты. Наудачу отбирается один телевизор для проверки. Какова вероятность того, что он не имеет скрытых дефектов?

53. Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть две партии из четырех или три из шести (ничьи во внимание не принимаются)?

Скачано с www.znanio.ru

Министерство образования и науки