Формирование познавательного интереса обучающихся  способом

дифференцированного обучения

 

 

Содержание

Введение. 2

Глава 1  Теоретические основы дифференциации обучения. 5

1.1 Сущность понятия «дифференциация обучения». 5

1.2 Возможности и пути использования дифференцированного обучения в формировании познавательного интереса в учебном процессе. 12

Глава 2   Из опыта использования дифференциации обучения в процессе преподавания математики. 22

2.1 Реализация способов дифференцированного обучения в формировании познавательного интереса на уроках математики. 22

2.2 Анализ опыта работы по реализации дифференцированного обучения. 25

Заключение. 37

Библиография. 39

 

 

Введение

 

Под влиянием возрастающих требований жизни увеличивается объем и усложняется содержание знаний, подлежащих усвоению. Но при традиционной системе обучения не каждый учащийся способен освоить программу. По своим природным способностям, темпу работы и т.д. учащиеся сильно отличаются друг от друга. Нередко в одной группе можно наблюдать обучающихся как с высоким, так и с очень низким уровнем развития. Преподаватель обычно выбирает методы и формы обучения, ориентированные на среднего учащегося. При этом слабым и сильным учащимся уделяется мало внимания. В этих условиях учащиеся с высокими способностями работают без особого напряжения, а слабые учащиеся испытывают возрастающие затруднения.

В обучении математике эта проблема занимает особое место, что объясняется спецификой этого учебного предмета. Математика является одной из самых сложных дисциплин и вызывает трудности у многих обучающихся. Как показали многочисленные психолого-педагогические исследования, если уровнять многие факторы, влияющие на уровень усвоения новых знаний, а именно: обеспечить одинаковый исходный минимум знаний у всех обучающихся, положительное отношение их к уроку, тщательно разработать методику введения нового материала, то, несмотря на равенство этих условий, новые знания будут усвоены по-разному. Одни учащиеся достаточно полно усвоят новое и могут применить его в новых, но сходных с учебной обстановкой условиях, требующих самостоятельного развития новых знаний (высший уровень усвоения). Другие усвоят существенные стороны нового понятия или закономерности и сумеют применить их к решению задач, близких к тем, которые разбирались в процессе объяснения нового материала (средний уровень усвоения). Наконец, будут и такие, кто вынес лишь отдельные, нередко несущественные стороны нового понятия или закономерности и не может применить их к решению даже простых задач (низший уровень усвоения). При этом потребуется различное количество упражнений и различная мера помощи со стороны преподавателя тем учащимся, которых предстоит довести до высшего уровня усвоения.

Следовательно, необходима такая организация учебного процесса, которая позволила бы учитывать  различия между учащимися и создавать оптимальные условия для эффективной учебной деятельности всех обучающихся, то есть возникает необходимость перестройки содержания, методов, форм обучения, максимально учитывающая индивидуальные особенности обучающихся. И подходом, который учитывает эти особенности, является дифференциация. Исходя из этого, мною была выбрана тема выпускной квалификационной работы: «Дифференцированное обучение в формировании познавательного интереса обучающихся».

 

Цель работы: реализация способов дифференцированного обучения и их влияние на формирование познавательного интереса обучающихся.

 

Задачи  работы ориентированы на реализацию цели:

1)      провести психолого-педагогический анализ информационных источников по проблеме   дифференциации обучения обучающихся;

2)      реализовать способы дифференцированного обучения обучающихся: дифференцированно-групповая работа, индивидуализированная самостоятельная работа;

3)      сделать анализ опыта работы по дифференцированному обучению обучающихся на дисциплине математика.

 

 

При написании работы использовались следующие методы:

-                   изучение и анализ психолого-педагогической, учебно-методической и другой литературы, посвященной изучаемой проблеме;

-                   наблюдения;

-                   беседы;

-                   анкетирования;

-                  анализ контрольных и самостоятельных работ по математике.

 

Глава 1  Теоретические основы дифференциации обучения

 

1.1 Сущность понятия «дифференциация обучения»

 

Личность каждого человека наделена только ей присущим сочетанием черт и особенностей, образующих её индивидуальность. Индивидуальность – это сочетание психологических особенностей человека, составляющих его своеобразие, его отличие от других людей. Индивидуальность проявляется в чертах темперамента, характера, привычках, преобладающих интересах, в качествах познавательных процессов (восприятия, памяти, мышления, воображения), в способностях, индивидуальном стиле деятельности и т.д. Нет двух людей с одинаковым сочетанием указанных психологических особенностей – личность человека неповторима в своей индивидуальности. Учет в обучении индивидуальных особенностей обучающихся является важной психолого-педагогической задачей. В психологии и педагогике существует понятие «индивидуальный подход» - это психолого-педагогический принцип, согласно которому в обучении учитывается индивидуальность каждого ребенка как проявление особенностей его психофизиологической организации в ее неповторимости, своеобразии, уникальности.

Необходимость такого подхода в разные времена отмечали многие ученые-педагоги. Например, В.А. Сухомлинский считал, что в обучении детей «нужны особые меры, необходим тонкий, деликатный индивидуальный подход» [17,т 1,с.92].

Необходимость учета индивидуальных особенностей обучающихся влечет за собой вопрос: как все это осуществить организационно. В аристократической системе домашнего обучения, где обучение было индивидуальным, эта проблема могла возникнуть только в  том смысле, способен ли преподаватель понимать индивидуальные особенности своего учащегося. Для современного школьного обучения все гораздо сложнее: обучающихся много, а преподаватель один, поэтому очень сложно построить учебный процесс в соответствии с индивидуальными особенностями каждого учащегося. Поэтому очень часто используется такой выход: выделяются отдельные группы обучающихся, обучение которых строится по-разному. Каждая группа обучающихся, имеющая сходные индивидуальные особенности, идет своим путем. В этом случае речь идет о дифференцированном обучении.

В 60-е годы XX века дифференцированное обучение применимо к общеобразовательной школе понималось как разделение школьных планов и программ в старших классах. В дальнейшем это понятие стало рассматриваться гораздо шире, но и здесь имеются различные подходы.

Например, И.Э.Унт подразумевает под дифференциацией учет индивидуальных особенностей в той форме, когда «учащиеся группируются на основании каких либо особенностей для отдельного обучения; обычно обучение в этом случае происходит по несколько различным учебным планам или программам»[18]. Примерно так же истолковывает это понятие и Е.С. Рабунский [13].

Гораздо шире рассматривает дифференцированное обучение И.М. Чередов. Он  включает в это понятие  не только обучение по различным планам и программам, но и «такой процесс обучения на уроках, который предполагает глубокое изучение индивидуальных особенностей обучающихся, их классификацию по типологическим группам и организацию работы этих групп над выполнением специфических учебных заданий, которые способствуют их умственному и нравственному развитию» [21].

Проблема дифференциации обучения принадлежит к традиционным для педагогики. В разное время эту проблему исследовали в своих работах различные авторы: А.А Бударный, З.И. Калмыкова [6], Е.С. Рабунский [13], И.Э.Унт [18], И.М. Чередов [21], Н.М. Шахмаев  и др. Их исследования показали эффективность и целесообразность дифференцированного обучения. Е.С. Рабунский считает, что «процесс обучения в условиях дифференциации становится максимально приближенным к познавательным потребностям обучающихся, их индивидуальным возможностям» [13]. И.М. Чередов отмечает, что «при дифференцированном обучении создаются оптимальные условия для активной деятельности всех обучающихся, обеспечивающие возможность продуктивного усвоения и переработки наибольшего количества информации » [21].

В ХХ веке в практике школ опробованы различные виды дифференциации обучения, среди них – дифференциация по способностям. На основании учета успеваемости в предыдущем классе учащиеся распределялись на несколько групп. Такое деление предполагалось ежегодным. Другой разновидностью дифференциации была дифференциация по интеллекту на основе интеллектуальных тестов. Третьей разновидностью являлась дифференциация обучения по неспособностям. Она состояла в том, что учащиеся, не успевающие по отдельным учебным предметам помещались в классы, в которых эти предметы изучались на пониженном уровне и в меньшем объеме. В 60-70-е гг. появилась такая форма организации дифференцированного обучения как специализированные школы с углубленным изучением отдельных учебных предметов.

В настоящее время выделяются два основных типа дифференциации обучения: внешняя и внутренняя.

Внешняя дифференциация характеризуется следующим:

§  Созданием однородных групп обучающихся по способностям, интересам, склонностям;

§  Организацией в этих группах однородной среды, предметно и социально жестко ориентированной (изучение отдельных предметов, их циклов, ориентация на подготовку в вуз с гарантией поступления в него и т.п.).

Внешняя дифференциация реализуется в организации работы профильных  классов, факультативов, гимназий и лицеев.

Внутренней дифференциации в отличие от внешней присущи следующие черты:

§  Создание смешанных (разнородных) классов, где детей изначально не разделяют по способностям.

§  Учет индивидуально - типологических особенностей детей осуществляется в специально созданных группах внутри класса; разделение на группы может быть явным или неявным, состав групп меняется в зависимости от поставленной учебной задачи.

  Следует  особо отметить уровневую дифференциацию как один из видов внутренней дифференциации. Впервые идея уровневой дифференциации была высказана в концепции дифференцированного обучения, разработанной РАО. В соответствии с ней уровневая дифференциация «предполагает такую организацию обучения, при которой учащиеся, обучаясь по одной программе, имеют право и возможность усваивать ее на различных планируемых уровнях, но не ниже уровня обязательных требований». Уровневая дифференциация основывается на планировании результатов обучения: явном выделении уровня обязательной подготовки и формировании на этой основе повышенных уровней овладения материалом. Сообразуясь с ними и, учитывая свои способности, интересы, потребности, учащийся получает право, и возможность выбирать объем и глубину усвоения учебного материала, варьировать свою учебную нагрузку.

В основе дифференцированного обучения лежит учет психологических особенностей обучающихся, а именно таких, которые влияют на их учебную деятельность и от которых зависят результаты учения. Это такие особенности как память, внимание, воображение, мышление, способности. Таких особенностей очень много, поэтому возникает вопрос: какие из них надо учитывать в первую очередь. Принцип индивидуального подхода в дидактике предполагает учет таких особенностей обучающихся, которые влияют на его учебную деятельность и от которых зависят результаты учения. Существует много типологий особенностей, разработанных различными учеными. Например, Ю.К. Бабанский определяет следующие критерии для определения учебных возможностей обучающихся и последующего разделения их на группы:

§  Уровень развития психических процессов и свойств в мышлении и в первую очередь умение выделять существенное в изучаемом, а также самостоятельность мышления обучающихся;

§  Сформированность навыков и умений учебного труда и, прежде всего, умение рационально планировать учебную деятельность, осуществлять самоконтроль в учении и выполнять в должном темпе основные учебные действия;

§  Отношение к учению, ведущие интересы и склонности;

§  Идейно-нравственная воспитанность, осознание необходимости учебной дисциплины, настойчивость при выполнении учебных требований;

§  Работоспособность;

§  Образовательная подготовленность по ранее пройденному материалу.

Другой ученый Е.С. Рабунский – к особенностям обучающихся, которые в первую очередь следует учитывать, относит:

§   Уровень успеваемости обучающихся, который, прежде всего, соответствует качеству выполнения ими учебных заданий. Преподаватель с помощью школьной отметки устанавливает уровень знаний и навыков обучающихся, согласно требованиям учебной программы,  а также относительный уровень умений – в соответствии с известными учителю алгоритмами усвоения и применения знаний;

§ Уровень познавательной самостоятельности. Познавательная самостоятельность в широком смысле слова – это готовность учащегося к самообразованию, это результат всей учебно-воспитательной работы в школе. В структуру познавательной самостоятельности входят знания, навыки, способности, мотивы учения;

§ Интересы, которые по принципу действенности можно условно подразделить на три уровня:

1)    Нулевой уровень характеризуется отсутствием интереса к предмету, такие учащиеся учатся, как правило, по принуждению;

2)    Потенциальный интерес к предмету характеризуется обычно положительным отношением к учению, любознательностью, желанием и отдельными попытками преодолеть трудности в учебной деятельности;

3)    Действенный интерес характеризуется осознанной устойчивой познавательной направленностью учащегося, основанной на глубокой потребности самостоятельно добывать знания, овладевать навыками, умениями [13].

А.А. Бударный берет за основу по преимуществу способность к учению и трудоспособность, при этом все-таки подчеркивается, что необходимо учитывать личность учащегося в целом – его интересы, отношение к учебе, эмоциональные и волевые качества.

И.Э.Унт выделяет следующие особенности:

§ Обучаемость, т.е. общие умственные способности (в том числе креативность), а также специальные способности;

§ Учебные умения:

§ Обученность, которая состоит как из программных, так и внепрограммных знаний, умений и навыков;

§ Познавательные интересы (на фоне общей учебной мотивации) [18].

Сопоставив мнения различных исследователей, о том, какие особенности обучающихся нужно учитывать в первую очередь при осуществлении дифференцированного подхода, можно сделать вывод, что очень важным для успешной организации обучения является уровень умственного развития, составляющими которого являются обучаемость и обученность.

Понятие «обучаемость» разработала психолог З.И. Калмыкова. Под обучаемостью понимают «систему интеллектуальных свойств личности, формирующихся качеств ума, от которых зависит продуктивность учебной деятельности»[6]. Среди слагаемых обучаемости – обобщенность мыслительной деятельности, экономичность, самостоятельность мышления, гибкость мыслительных процессов и т.д. Исследования подтвердили существование как общей обучаемости (общей способности к учению), так и специальной (способности к изучению какого-то учебного предмета).

Кроме обучаемости уровень умственного развития учащегося определяют также и знания, умения и навыки, или обученность. Умственные способности представляют собой потенциальные возможности, предпосылки для учения, знания же являются содержательной базой для реализации способностей. Учащиеся с высоким уровнем знаний, умений и навыков усваивают новый учебный материал значительно легче, чем те, у кого этот уровень низок.

Кроме того, ученые отмечают, что в процессе обучения необходим учет познавательных интересов. Под познавательным интересом к предмету понимают избирательную направленность психических процессов человека на объекты и явления окружающего мира, при которой наблюдается стремление личности заниматься определенной областью деятельности. Познавательные интересы в процессе обучения учитываются как с целью повышения мотивации активной работы, так и с целью углубления имеющихся интересов и формирования новых.

Учет вышеперечисленных показателей важен для всех обучающихся. В отдельных случаях к этим особенностям добавляются и такие факторы, которые в отношении данного ребенка оказывают специфическое влияние на учебную деятельность (особенно важны среди этих факторов домашние воспитательные условия). Кроме психологических факторов на учебный процесс свое влияние оказывает и состояние здоровья ребенка. Болезни, в зависимости от их характера, оказывают на обучающихся временное или постоянное отрицательное воздействие – снижают его трудоспособность. Различные физические дефекты (расстройство зрения, слуха, задержки в умственном развитии) делают невозможным нормальный процесс учебно-познавательной деятельности и обусловливают необходимость в специальном обучении.

Из всего выше сказанного можно сделать вывод, что дифференцированный подход – это такая система обучения, которая ставит своей целью создание оптимальных условий для выявления задатков, развития интересов и способностей; она характеризуется формированием групп обучающихся, сходных по какому-либо комплексу качеств, среди которых основными являются обучаемость, обученность, познавательный интерес; кроме того, имеется ряд специфических факторов (состояние здоровья, домашние воспитательные условия и т. д.). 

 

1.2 Возможности и пути использования дифференцированного обучения в формировании познавательного интереса в учебном процессе

 

В настоящее время появились различные учебные заведения нового типа (гимназии, лицеи, колледжи и.т.д.), в организации работы которых, реализуется  внешняя дифференциация. В таких образовательных учреждениях создаются более благоприятные, чем в обычных образовательных учреждениях условия для учета учебных возможностей обучающихся. Но все же большинство ребят школьного возраста учатся в обычных средних школах, училищах. Поэтому возникает вопрос: как можно осуществить дифференциацию обучения в учреждении НПО.

Основной формой организации обучения в училище является урок, который характеризуется разнообразием способов организации учебной деятельности. Выделяют следующие формы учебной работы на занятии:

-                  фронтальная;

-                  групповая;

-                  индивидуальная.

Выясним, какие возможности для дифференциации предоставляет каждая форма работы.

При фронтальном обучении педагог управляет учебной деятельностью всего класса, который работает над единой задачей. Он осуществляет прямое идейно-эмоциональное воздействие на коллектив обучающихся, организует их сотрудничество, определяет им единый темп работы. Однако фронтальная форма организации обучения не рассчитана на учет индивидуальных различий обучающихся. Взятый темп урока слабым учащимся может показаться высоким, а сильным – низким. По этой причине слабые учащиеся уйдут с занятия, не усвоив учебный материал. Сильные же недостаточно расширят и углубят знания.

Характеризуя вторую форму учебной работы – групповую, нужно отметить, что еще К.Д.Ушинский, рассматривая вопросы организации учебного процесса в школах, рекомендовал делить группу на подгруппы для того, чтобы давать всем детям задания в соответствии с их подготовкой. Он писал: «Такое деление класса на группы, из которых одна сильнее другой, не только не вредно, но даже полезно, если наставник умеет, занимаясь с одной группой сам, дать двум другим полезное самостоятельное упражнение» [19].

Что же такое групповая работа? По определению Х.И. Лийметса, под групповой работой мы понимаем «такое построение работы, где класс делится для выполнения того или иного задания на группы по 3-8 человек – чаще всего по 4 человека. Задание дается группе, а не отдельному учащемуся».

Исследователи отмечают, что в малой группе учащийся находится в более благоприятных,  чем при фронтальной работе всем классом условиях в отношении возможности действовать в соответствии со своей индивидуальностью. В беседе внутри малой группы он может высказывать свое мнение, активнее участвовать в решении учебных задач в соответствии со своими интересами и способностями.

И.М. Чередов подразделяет групповую форму учебной работы на звеньевую, бригадную, кооперированно-групповую и как особую разновидность групповой формы обучения, которая предполагает организацию работы групп обучающихся с разными учебными возможностями, выделяет дифференцированно-групповую форму [21]. Она позволяет, зная индивидуальные особенности каждого учащегося (уровень подготовки, развития, особенности мышления, памяти, интерес к предмету и т.д.), определить для него наиболее целесообразный и эффективный характер работы на занятии.

 Дифференцированно-групповая работа предполагает организацию работы групп с разными учебными возможностями, поэтому возникает следующий вопрос: как сгруппировать обучающихся для работы на занятии? Наиболее сложной и в то же время основной проблемой становится выбор тех свойств обучающихся, на основе которых их группируют. В педагогической литературе часто ограничиваются выражениями «сильный», «средний» и «слабый» учащийся, не уточняя, в каком отношении он силен или слаб. Как уже указывалось выше, разные ученые берут разные критерии за основу группировки обучающихся. Например, Е.С. Рабунский исходит из уровня успеваемости, степени познавательной самостоятельности и из активного интереса к учебе. А.А. Бударный берет за основу способность к учению и трудоспособность. Но  все же неясно, в какой мере при такой группировке учитывается то или иное свойство учащегося.

 Фактически все сводится к одному вопросу: что считать существенным при группировке обучающихся – уровень их знаний или способностей, особенно если речь идет об обучающихся, у которых эти свойства не согласуются. В какую группу поместить обучающихся, которые занимаются довольно хорошо, но которые не в состоянии выполнить задания труднее обычных, а также таких обучающихся, которые успешно выполняют задания, требующие сложных мыслительных операций, но чей уровень знаний при этом остается средним или даже ниже среднего?

 И.Э.Унт решает этот вопрос таким образом - создаются разные группы в зависимости от того, каких свойств учащегося данные задания больше требуют – умственных способностей или уровня знаний [18]. Здесь следует отметить, что в групповой работе распространено деление обучающихся  на две категории по способу работы:

-             работа с относительно стабильными группами;

-             работа с нестабильными группами.

В случае каждого способа работы можно создать группы различного состава.

Первый способ в организационном отношении более удобен для преподавателя и экономичен по времени, поскольку каждый учащийся знает, в какую группу он входит. Учителю стоит лишь назвать номер группы, чтобы учащиеся могли приступить к работе. Однако этот способ не такой гибкий при учете индивидуальных способностей обучающихся. И наоборот, второй способ неудобен в организационном отношении и требует больше времени (преподаватель должен всякий раз назначать, кто какое задание выполняет), но он более гибкий при учете индивидуальности учащегося, поскольку в каждом конкретном случае можно учитывать существенные для данной работы индивидуальные особенности. Преподаватель должен выбрать для себя наиболее приемлемый способ работы.

 Дифференцированно-групповая форма  работы  требует от преподавателя тщательного изучения индивидуальных особенностей обучающихся, правильного определения их учебных возможностей. Знание этих возможностей позволяет подбирать оптимальные условия для развития каждого учащегося. Среди особенностей обучающихся, которые необходимо учитывать при организации дифференцированного обучения, доминируют обученность, обучаемость и познавательный интерес, поэтому остановимся подробнее на проблемах диагностики этих качеств.

Основным методом диагностики уровня обучаемости в педагогике долгое время был обучающий эксперимент, с помощью которого прослеживается  проявление способностей в процессе усвоения нового материала. Так, например, З.И.Калмыкова рекомендует для диагностики умственных способностей обучающий эксперимент, в ходе которого учащиеся выполняют задания проблемного характера [6]. Подобную же методику использовал и В.А.Крутецкий при исследовании математических способностей [8]. В своих позднейших исследованиях З.И.Калмыкова выработала методику оценки умственных способностей обучающихся, когда оценочные суждения определяются тем, в какой степени учащиеся оказываются способны самостоятельно проработать новый учебный материал.

Другим основным методом диагностирования уровня обучаемости обучающихся является метод тестирования. В этом случае учащимся предъявляются задания, не связанные с учебным материалом. Их выполнение требует участия различных познавательных процессов. По качеству выполнения предложенных заданий и определяется уровень обучаемости обучающихся.

Что касается специальной обучаемости (способности к изучению какого-то учебного предмета), ее диагностика осуществляется аналогично общей обучаемости – с помощью обучающего эксперимента и тестов. Для диагноза специальных способностей используется такой  вид учебной деятельности, который предполагает наличие соответствующих способностей; например, решение математических задач дает примерное представление относительно соответствующих способностей у учащегося.

Изучив обучающихся с помощью выделенных методик, преподаватель определяет уровень обучаемости каждого учащегося.

Высший уровень обучаемости отличает тех ребят, которые свободно анализируют материал, выделяя существенные признаки, быстро обобщают, абстрагируют, легко выводят новые понятия, имеют прочные навыки планирования, самоконтроля, обладают способностью свободно совершенствовать разные учебные операции.

 Высокий уровень обучаемости наблюдается у тех обучающихся, которые испытывают некоторые затруднения только при анализе материала с весьма сложной структурой, во всех других ситуациях свободно отделяют существенные признаки от несущественных, в большей части обладают самостоятельностью мышления, сформированными умениями планирования, навыками самоконтроля, свободно совершают разные учебные операции.

Средний уровень обучаемости наблюдается у тех обучающихся, которые испытывают трудности в анализе материала, в выделении существенных признаков, но с помощью преподавателя справляются с заданием; такие учащиеся зачастую не отличаются самостоятельностью мышления, слабо владеют учебными умениями и навыками, не умеют рационально планировать, осуществлять самоконтроль.

Наконец, низкий уровень обучаемости  характеризует тех обучающихся, которые испытывают большие трудности в анализе материала, выделении существенных признаков понятий, обобщении, абстрагировании, слабо владеют или совсем не владеют умениями и навыками умственного труда.

Помимо обучаемости преподаватель также должен определить уровень обученности обучающихся. Одним из ориентиров для определения уровня обученности обучающихся являются оценки, выставленные за ранее изученный материал в классных журналах. Для более точного определения этого качества необходимо тщательно наблюдать за учебной деятельностью обучающихся, проводить с ними диагностирующие работы. Одним из наиболее эффективных и удобных методов диагностики являются предметные тесты. Они состоят из коротких заданий, на которые учащийся должен реагировать или составлением ответа (что часто представляет собой заполнение пробелов), или комбинированием предложенных ему готовых ответов (выбор правильного ответа, объединение подходящих элементов, суждение о правильности представленных ответов и т.д.).

Пригодность предметных тестов для диагностики знаний вытекает из того, что этот вид контроля дает возможность составлять вопросы в объеме всего предметного курса, к тому же результаты их хорошо сравнимы между собой.

 Чтобы определить общий уровень обученности обучающихся, можно воспользоваться следующими критериями. Высший уровень обученности отмечается у тех обучающихся, которые в любой ситуации учебного процесса демонстрируют высокие знания ранее изученного материала, свободно ими пользуются при анализе нового материала для выделения существенных признаков, обобщения, выведения новых понятий, усвоения новых знаний. Высокий уровень у тех обучающихся, которые в большей части учебных ситуаций показывают высокие знания, свободно на них опираются при анализе нового материала, выведении понятий, усвоении знаний. Те учащиеся, которые не всегда располагают определенным фондом действенных знаний при анализе нового материала, испытывают затруднения при выведении новых понятий, обладают средним уровнем обученности. Низкий уровень характеризует тех обучающихся, которые, имея ограниченный фонд действенных знаний, не могут успешно анализировать новый материал, выводить новые понятия, закономерности.

Для изучения познавательных интересов наиболее распространенными методами являются наблюдение, беседа, сочинения и анкеты. Для изучения интересов используется и диагноз знаний. При этом исходят из факта, что учащийся, интересующийся какой-либо областью знаний, обладает здесь значительно большими знаниями. Так, например, диагноз предварительных знаний можно использовать и для изучения интересов.

Г.И.Щукина в своих исследованиях подразделяет обучающихся по характеру познавательных интересов на три категории [23].

 Учащиеся с высоким уровнем развития познавательных интересов отличаются высокой самопроизвольной познавательной активностью. Они проявляют интерес к сущности явлений, всегда стремятся разобраться в трудных вопросах. Поэтому интенсивно и с увлечением самостоятельно работают. Особенно с большим желанием решают сложные задачи, любят преодолевать трудности.

Учащиеся со средним уровнем развития интереса, по мнению Г.И.Щукиной, проявляют познавательную активность при побуждении преподавателя. Они интересуются только информацией, дающей определенные факты, описание, сущность же явлений выясняют только с помощью преподавателя. Проявляют интерес к самостоятельной работе в зависимости от ситуации при наличии побуждений извне. Эти учащиеся трудности преодолевают при помощи преподавателя.

Учащиеся с низким уровнем познавательного интереса отличаются познавательной инертностью. Они демонстрируют эпизодический интерес к эффектным и занимательным сторонам явлений при полном отсутствии его к их сущности. Эти дети отличаются мнимой самостоятельностью в работе, часто отвлекаются при затруднениях, пасуют, их характеризует полная бездеятельность.

Преподаватель, выбрав для себя наиболее приемлемые методы диагностики, определяет учебные возможности обучающихся, относит каждого учащегося к той или иной типологической группе и осуществляет обучение, ориентируясь на это деление.

Третья форма учебной работы на занятии – индивидуальная – представляет собой такую организацию обучения, где каждый учащийся работает самостоятельно, проявляя инициативу. Темп работы зависит от учебных возможностей и подготовленности учащегося. Дифференциацию  обучения здесь можно осуществить с помощью индивидуализированной самостоятельной работы. Она состоит в том, что учащимся даются не одинаковые задания, а задания, которые варьируются в зависимости от особенностей обучающихся. Преподаватель предлагает задания соответствующего типа каждой группе обучающихся. Определив группам задания разных типов, преподаватель наблюдает за самостоятельной работой обучающихся. Особенно внимательно он следит за учащимися с низкими учебными возможностями. В необходимых случаях приходит им на помощь. Он должен иметь в виду, что эти учащиеся с робостью берутся за выполнение задания, у них нет полной уверенности в том, что они сумеют это сделать.

Рассмотрим, как дифференциация может включаться в процесс обучения.

При формировании знаний работа может быть организована следующим образом. Преподаватель сначала излагает материал всем, затем учащимся с высокими учебными возможностями  предлагает работать с другими источниками знаний, а с остальными разбирает материал вторично, уточняя отдельные моменты, еще раз аргументируя основные положения. На этом этапе учащиеся со средними и низкими учебными возможностями, отвечая на вопросы преподавателя, обобщают и систематизируют знания. Учащиеся с высокими учебными возможностями, отличающиеся познавательной самостоятельностью, расширяют и углубляют знания.

Самые широкие возможности для дифференциации предоставляет этап закрепления и применения знаний. На этом этапе урока необходимы, прежде всего, групповые занятия обучающихся, в ходе которых они бы выполняли конкретные задания, соответствующие их учебным возможностям. Задания в зависимости от уровня группы различны по трудности и по количеству. Работа в группах происходит следующим образом: учащиеся знакомятся с заданием, все приступают к его выполнению. Если результат у всех одинаковый, то выполняют другое задание. Если кто-то получил другой результат, чем другие, он должен объяснить, как его нашел и по возможности найти ошибку. При необходимости ему помогают. Если получено несколько разных ответов, то все члены группы еще раз анализируют процесс решения, а за этим следует общий анализ. Если какая-либо группа испытывает трудности, преподаватель включается в ее работу и руководит обсуждением. Таким образом, преподаватель больше внимания может уделить учащимся, чем в рамках фронтальной работы.

Много возможностей для дифференциации на этапе закрепления и применения знаний имеется и у индивидуализированной самостоятельной работы.

 При организации индивидуализированной самостоятельной работы преподаватель может руководствоваться следующими схемами:

Схема 1:

1) Общие задания;

2) Дополнительные задания более быстрым и сильным учащимся.

Схема 2:

1) Общие задания;

2) Разветвленные задания

-                  более легкий вариант

-                  средний вариант

-                  более трудный вариант.

Схема 3:

Разветвленные задания

- более легкий вариант

- средний вариант

- более трудный вариант.

Схема 4:

1) Разветвленные задания

- более легкий вариант

- средний вариант

- более трудный вариант.

2) Общие задания.

Использование схемы 1 целесообразно при изучении такой новой темы, которая содержит много нового учебного материала и поэтому заставляет быть в напряжении не только слабых, но и сильных обучающихся. Схема учитывает различный темп продвижения обучающихся и в заключение предлагает дополнительные задания более быстрым учащимся.

Схема 2 эффективна тогда, когда не представляется целесообразным заставлять всех обучающихся в полном объеме выполнять общие задания, поскольку это оказалось бы для части обучающихся слишком легким, а для части – слишком трудным. Схема приемлема, например, в том случае, когда новый материал содержал элементы повторения или когда имеют дело  с упражнениями после прохождения теоретических основ темы.

Схема 3 используется тогда, когда подготовка и способности обучающихся настолько различны, для усвоения нового материала, что общие задания не могут обеспечить развивающей деятельности для большинства обучающихся. Такое положение типично для повторения, а также в случае слишком различных предшествующих знаний.

Схема 4 целесообразна в том случае, когда между учащимися наблюдаются большие различия в таких предварительных знаниях, которые необходимы для изучения нового учебного материала. В таком случае разветвленные задания подготавливают восприятие и понимание новой темы, а их выполнение способствует переходу к общим заданиям.

Кроме того, можно использовать различные комбинации этих схем.

Эффективным средством для учета интересов и способностей обучающихся являются и дифференцированные домашние задания, которые могут быть направлены на дальнейшее изучение нового материала, на закрепление и проверку знаний, умений и навыков обучающихся. Например, домашние задания могут включать в себя задания по написанию рефератов (для сильных обучающихся) с последующим выступлением на кружке, факультативе, внеклассном мероприятии. При изучении математики можно предлагать учащимся для домашнего решения задачи разного уровня сложности,  разное количество задач.

Это некоторые из способов реализации дифференциации в процессе обучения. Число и разнообразие этих способов зависит от творческой направленности и фантазии преподавателя, от его индивидуальных склонностей, педагогического мастерства, от умения работать сразу со всем классом, и с отдельным учащимся в отдельности.

Глава 2   Из опыта использования дифференциации обучения в процессе преподавания математики

 

2.1 Реализация способов дифференцированного обучения в формировании познавательного интереса на уроках математики

 

Дифференциация обучения обучающихся осуществлялась на уроках по следующим темам:

    Алгебра:

- Таблица первообразных (см. приложение 1).

- Правила нахождения первообразных (см. приложение 2).

Геометрия:

- Простейшие задачи в координатах (см. приложение 3, 4).

 

Занятия были построены с учетом различий в уровнях знаний и способностей обучающихся. Одной из целей уроков было развитие познавательного интереса к математике, которому способствовали необычные формы проведения уроков, личное участие каждого учащегося в работе, чувство ответственности, осознание каждым учащимся своей возможности чего-то достичь.

Приведем пример использования дифференциации на конкретном занятии.

 

Урок «Правила нахождения первообразных».

Цель урока: выработка умений находить первообразную, график которой проходит через данную точку и первообразные в случаях, непосредственно сводящихся к применению таблицы первообразных и трех правил нахождения первообразных.

На этом занятии дифференцированное обучение применяется на этапе закрепления изученного материала (дифференцированно-групповая работа).

Учащиеся рассаживаются по группам (группы 1, 2, 3 ).

1 группа – учащиеся с высоким уровнем развития познавательных интересов с высокой самопроизвольной познавательной активностью. Они проявляют интерес к сущности явлений, всегда стремятся разобраться в трудных вопросах. Поэтому интенсивно и с увлечением самостоятельно работают. Особенно с большим желанием решают сложные задачи, любят преодолевать трудности.

2 группа – учащиеся со средним уровнем развития интереса, проявляющие познавательную активность при побуждении преподавателя. Они интересуются только информацией, дающей определенные факты, описание, сущность же явлений выясняют только с помощью преподавателя. Проявляют интерес к самостоятельной работе в зависимости от ситуации при наличии побуждений извне. Эти учащиеся трудности преодолевают при помощи преподавателя.

3 группа – учащиеся с низким уровнем познавательного интереса, отличающиеся познавательной инертностью. Они демонстрируют эпизодический интерес к эффектным и занимательным сторонам явлений при полном отсутствии его к их сущности. Эти дети отличаются мнимой самостоятельностью в работе, часто отвлекаются при затруднениях, пасуют, их характеризует полная бездеятельность.

         Каждой группе выдается карточка. Дается следующая устная инструкция по выполнению заданий: «Познакомьтесь с заданием, затем приступайте к решению. Если результат у всех одинаковый, то решайте другую задачу. Если кто-то получил другой результат, чем другие, он должен объяснить, как решал и по возможности найти ошибку. При необходимости можно помочь ему. Если получено несколько разных ответов, то все члены группы еще раз анализируют весь ход решения».

 

Карточка группы 1:

1.     Для функции f найдите первообразную, график которой проходит через данную точку:              

2.     Докажите, что разность первообразных для функции f(x) = 2 - sin 2x  в     точках М(1;3),  N(2;4) равна 4.

3.     При каких а функция F=x sin x + a cos x является первообразной для функции F= x cos x?

 

Карточка группы 2.

1.Для функции f найдите первообразную, принимающую заданное значение в данной точке:             F(-1) = 4.

2.Для функции f найдите две первообразные, расстояние между соответствующими точками графиков которых (т.е. точками с равными абсциссами) равно а:   f(x) = 2 – sin x,   a = 4.

3.Найти общий вид первообразных для функции  f(x) = (5 + 2x)⁶_.

 

Карточка группы 3.

1. Для функции f найдите первообразную, принимающую заданное значение в данной точке:          f(x)=x³     F(-1) = 2.

2. Для функции f найдите первообразную, график которой проходит через данную точку:          f(x) = 3x² - 2x + 4,      M (-1;1)

3. Найти общий вид первообразных для функции f(x) = (3 + 2x)²

 

 

 

  2.2 Анализ опыта работы по реализации дифференцированного обучения

 

Опытная работа по дифференциации осуществлялась на втором курсе. Данная работа проводилась в несколько этапов. На первом этапе была проведена диагностическая работа по выявлению индивидуальных особенностей каждого учащегося, были выделены временные типологические группы для работы на уроках и составлен план дифференцированного обучения. Вторым этапом опытной работы было проведение уроков с использованием дифференциации. На заключительном, третьем этапе, были проведены проверочные работы для оценки результатов примененной системы обучения. Теперь подробнее о каждом этапе.

1 этап:

На втором курсе в группе № 132 по специальности «Машинист локомотива» обучалось 25 обучающихся – все юноши. Возраст обучающихся – 15-16 лет. Большинство обучающихся группы имеют средние и слабые знания в области математики, частично опираются на изученную в курсе 9-ти летней школы теорию, при изучении нового материала и при решении примеров. Но, кроме того, имеются 8 обучающихся, которым необходимо пристальное внимание со стороны преподавателя математики, так как они имеют большие пробелы в знании программного материала, не могут применить имеющиеся знания на практике, то есть обладают низким уровнем обученности. Эти данные получены с помощью анализа знаний и умений по математике на основе нулевого среза, а также отметок в аттестатах. На основе этих данных построена диаграмма 1.

Диаграмма 1

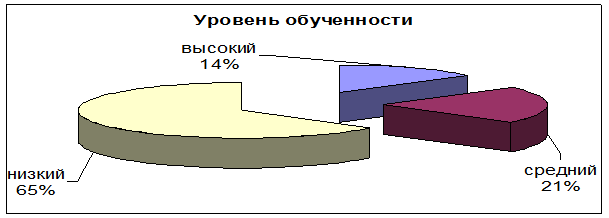
Пояснение к диаграмме:

- высокий уровень обученности -  учащийся в любой ситуации учебного процесса демонстрирует высокие знания ранее изученного материала, высокий уровень математических умений и навыков;

- средний уровень обученности – учащийся не всегда располагает необходимым фондом знаний, умений и навыков при изучении математики;

- низкий уровень обученности - учащийся, имеет ограниченный фонд знаний, умений и навыков.

А также установлено, что более половины обучающихся группы имеют  уровень обучаемости, достаточный для  изучения программного материала. В качестве метода исследования обучаемости был выбран анализ процесса решения экспериментальных задач. Задания были подобраны так, чтобы они требовали не воспроизведения известных алгоритмов решения, а самостоятельного нахождения пути решения задачи. Учащимся была предложена самостоятельная работа из 3-х заданий, а также числовой тест (см. приложения 5 и 6).

Результаты этих работ отражены в диаграмме 2.

Диаграмма 2

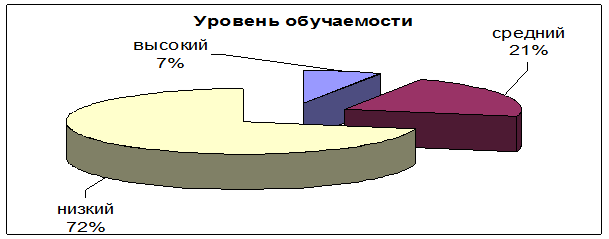
Пояснение к диаграмме:

- высокий уровень обучаемости – учащийся свободно анализирует материал, обладает способностью самостоятельно найти путь решения задачи нового типа;

- средний уровень обучаемости - учащийся испытывает трудности в анализе материала, решении задач нового типа, но с помощью преподавателя справляется с заданием;

- низкий уровень обучаемости -  учащийся испытывает большие трудности в анализе материала, слабо владеет или совсем не владеет умениями и навыками умственного труда, не способен выполнить задание, требующее самостоятельного нахождения пути решения.

На основании вышеприведенных данных можно выделить следующие группы:

 1 группа – обладающие высоким уровнем математических знаний, умений и навыков, самостоятельно и творчески мыслящие.

 2 группа – обладающие достаточно хорошим уровнем математических знаний, умений и навыков, но испытывающие трудности при решении задач нового типа.

3 группа – имеющие низкий уровень математических знаний, умений и навыков, не способные решить новую задачу.

Характеризуя отношение к учению, интересы и склонности обучающихся данной группы, нужно отметить следующее. Лишь один учащийся группы имел прочный устойчивый интерес к математике. Учащийся в свободное время с большим желанием решал математические задачи, преодолевал трудности при выполнении различных примеров.    

Диагностика уровня интереса обучающихся к предмету была проведена с  помощью мониторинга, который охарактеризовал  всех обучающихся по нескольким показателям. Все данные отражены в таблице 1.

Таблица 1

«Уровень сформированности качеств, характеризующих интерес к математике»

 

Пояснение к таблице.

Наличие самостоятельности при решении познавательных задач:

1-    учащийся не может работать без помощи преподавателя.

2-    учащийся проявляет интерес к самостоятельной работе в зависимости от ситуации при наличии контроля со стороны преподавателя.

3-    учащийся всегда проявляет высокую самостоятельность, стремится сам разобраться в трудных вопросах.

     Отношение к творческим поисковым задачам:

 1- учащийся не любит решать сложные задачи, при малейших трудностях пасует.

 2- учащийся любит решать творческие поисковые задачи, но, испытав затруднение при решении, сразу обращается за помощью к товарищам или преподавателю.

 3- учащийся с большим желанием решает сложные задачи, любит преодолевать трудности.

  Осведомленность в области математики:

 1 - низкий уровень математических знаний, умений и навыков.

 2 - средний уровень математических знаний, умений и навыков.

 3 - высокий уровень математических знаний, умений и навыков.

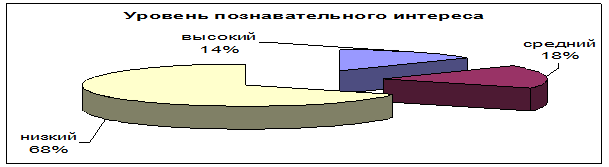
На основании данной таблицы, с учетом классификации Г.И.Щукиной (см. пункт 1.2) учащиеся были распределены по уровням познавательного интереса. По данным таблицы построим диаграмму 3:

Диаграмма 3

2 этап:

На втором этапе исследования нами использовались способы реализации дифференцированного обучения обучающихся:

- дифференцированно-групповая работа;

- индивидуализированная самостоятельная работа.

Система этих способов реализовывалась в течение одного года обучения математике на втором курсе.

Так, например, нами исследовались возможности применения дифференциации на этапе закрепления знаний. Рассмотрим проблему дифференцированной помощи учащимся при решении задач.

  Выделим три группы обучающихся в соответствии с уровнем сформированности  у них умений по решению задач.

Учащиеся первой группы имеют пробелы в знаниях программного материала, искажают содержание теорем в применении их к решению задач, самостоятельно могут решить задачи в один - два шага, решение более сложных задач начинают наугад, не умеют вести целенаправленный поиск решения, не могут найти связи между данными и искомыми величинами, часто пропускают обоснование доказанных фактов, сформулированных в ходе попыток решения, и не понимают необходимости их проведения, не видят существенных зависимостей и ключевых моментов в решении задач.

Эта общая характеристика не исключает различных индивидуальных особенностей обучающихся, входящих в первую группу. Здесь могут быть учащиеся, имеющие пробелы в знаниях и отставание в развитии вследствие частых пропусков уроков по болезни, в силу систематической плохой подготовки к урокам. Вместе с тем эту группу составляют учащиеся, относящиеся к разным уровням обучаемости.

Учащиеся второй группы имеют достаточные знания программного материала, могут применить их при решении стандартных задач. Затрудняются при переходе к решению задач нового типа, но, овладев методами их решения, справляются с решением аналогичных задач; не справляются самостоятельно с решением сложных (нетиповых) задач. У этих обучающихся не сформированы эвристические приемы мышления, они с большим трудом могут сформулировать  цель в процессе поиска решения задачи.

Третью группу составляют учащиеся, которые могут сводить сложную задачу к цепочке простых подзадач, выдвигать и обосновывать цели в процессе поиска решения задач, переносить прежние знания в новые условия. Эти учащиеся быстро и легко обобщают методы решения классов однотипных задач.

Все вышесказанное не означает, что учащиеся первой группы должны решать только простые задачи, объясняя это тем, что обычные способы решения затормаживают мышление, следовательно, тормозят развитие. Поэтому все три группы наряду с простыми задачами должны решать сложные. Учащиеся всех трех групп могут решать одну и ту же сложную задачу, но мера помощи преподавателя каждой из групп будет разной.

Такая система обучения позволяет даже слабому учащемуся перейти в дальнейшем в группу более высокого уровня, так как обучающихся учат не просто воспроизводить ход решения задачи, но и вести поиск в разных направлениях.

Вообще, работа со слабыми учащимися должна занимать очень важное место в обучении. Но несмотря на это, очень часто учащиеся, которые по каким-то причинам не усвоили материал, часто не получают никакой поддержки и помощи со стороны преподавателей.

При подготовке к уроку преподаватель должен выписать формулы, отдельные фрагменты решения примеров, которые будут рассматриваться на занятии, теоремы, которые будут использованы во время урока, и начинать урок с их повторения – это так называемая актуализация прежних знаний. Ее можно проводить фронтально, у доски, вызывая обучающихся по их желанию. В любом случае на повторение нельзя тратить более 5 минут, поэтому рассматриваемые вопросы необходимо заранее написать на доске или воспользоваться проектором. Ответы обучающихся не оцениваются отдельной оценкой, но учитываются в дальнейшем.

При проведении практических уроков по решению примеров, уравнений по темам «Производная», «Степень с рациональным показателем», «Решение тригонометрических, показательных, логарифмических и иррациональных уравнений» и др. (т.е. по темам, где на решение задания затрачивается немного времени) – преподаватель поступает следующим образом: сначала решает уравнение определенного типа сам с подробным объяснением, потом вызывает к доске 5 человек (желающих): трех обучающихся средних способностей, двух послабее. Каждому дается свое задание, подобное разобранному учителем (можно пользоваться тетрадью). Перед всем классом ставится задача: решить все записанные на доске примеры самостоятельно, не дожидаясь записей на доске (на оценку).

Очень часто, нами - преподавателями допускается ошибка – боимся поставить учащемуся хорошую отметку, так как примеры однотипные и не требуют большой сообразительности. Все это приводит к тому, что учащиеся становятся пассивными, равнодушными к предмету. Ведь если учащийся систематически не занимается, то полученная случайно четверка затеряется среди других отметок. Но в то же время хорошая отметка может пробудить уверенность в своих силах, самоуважение, желание лучше учиться, интерес к предмету.

Итак, 5 человек у доски 2-3 минуты пытаются решать задание самостоятельно, потом преподаватель начинает помогать каждому из них по очереди: сначала первый пример подробно разбирается и повторяется вместе с отвечающим, второй пример разбирается уже менее подробно и так до тех пор, пока все примеры будут решены.

После этого проводится самостоятельная работа: всем раздаются карточки с заданиями (желательно иметь 6 и более вариантов). После того как учащиеся начали работать, преподаватель проходит по классу и тех ребят, которые не знают с чего начать, вызывает к доске и снова подробно объясняет на подобном примере решение. И даже после этого следует подходить к работе обучающихся дифференцированно. Если преподаватель видит, что на самостоятельную работу осталось мало  времени, и многие еще не успели выполнить задание, то на проверку разрешает сдать работу только желающим. Остальные должны переписать полностью свои задания и решить их дома. И только те учащиеся, которые не выполнят задания к следующему уроку, получают двойку.

Контрольные работы проводятся по индивидуальным карточкам с использованием справочного материала, подготовленного самими учащимися. Если контрольная работа написана на «2», то учащийся обязан сделать либо работу над ошибками сам, либо с помощью преподавателя на консультации. Если учащийся хочет исправить отметку «3» на «4» или «5», то ему необходимо сделать работу над ошибками (можно дома), а потом на дополнительном занятии написать другой вариант.

Рекомендуем проводить со слабыми учащимися математические диктанты, цель которых – помочь учащимся запомнить формулировки аксиом и теорем, которые в дальнейшем будут использованы.

   В результате такой систематической работы, у ребят появляется интерес к предмету, желание трудиться. Они уже с удовольствием выходят к доске, не боятся отвечать. В результате увеличивается количество хороших отметок по математике.

Кроме того, обратим внимание на организацию контроля домашнего задания. К этой форме контроля не обязательно привлекать хорошо успевающих обучающихся, здесь может справиться любой. На каждую тему или блок тем выбирается несколько контролеров, которые перед каждым уроком математики проверяют у ребят определенной группы наличие домашней работы (причем контролер должен быть из другой группы). В течение учебного года к этой работе будет привлечена вся группа. Таким образом, практически каждый учащийся выполняет  посильную работу по организации учебного процесса.

Хочется отметить реальную пользу от применения деталей дифференцированного обучения:

-       Значительно улучшается четкость в организации работы группы; 

-       Так как каждый учащийся работает на посильном для него уровне трудности, он лучше осознает свои ближайшие цели и задачи;

-       Четкость в работе дает возможность постоянно контролировать знания, умения и навыки;

-       Наличие сильных обучающихся как группы позволяет постоянно продумывать работу с ними, учитывать возможности их развития.

На основе вышесказанного можно заключить, что использование дифференциации обучении обучающихся эффективно и целесообразно.

 

3 этап:

На завершающем этапе исследования с учащимися были проведены две работы:

- контрольная работа по геометрии;

- самостоятельная работа по алгебре (см. приложения 7 и 8).

Обе работы требовали применения полученных знаний, умений, навыков и содержали как задания на воспроизведение известных  алгоритмов решения, так и задачи на самостоятельный творческий поиск решения. По итогам проверки этих работ и обобщения их результатов было снова составлено распределение обучающихся по уровням обученности и обучаемости (см. приложения 9 и 10 ).

Таблица 2

Уровень обученности

 

Диаграмма 4

 

 

 

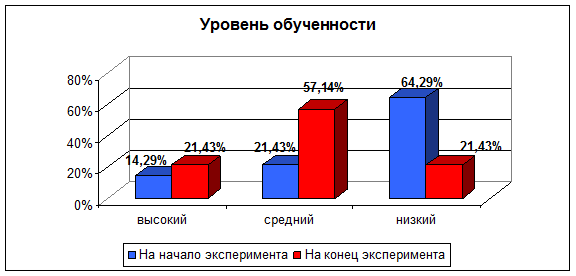
Таблица 3

Уровень обучаемости

 

Диаграмма 5

 

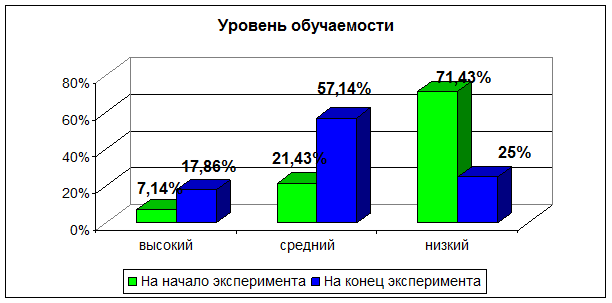
После диагностики произведено распределение обучающихся по уровням познавательного интереса (см. приложение 11), и результаты сравнены с результатами до проведения опытной работы.

Таблица 4

Уровень познавательного  интереса

	На начало эксперимента	На конец эксперимента
Высокий	4	4
Средний	5	18
Низкий	19	6

 

 

 

 

 

 

 

Диаграмма 6

 

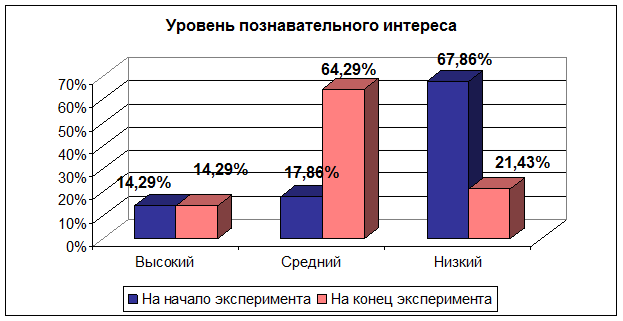
Анализ таблиц, сравнивающих уровни развития исследуемых показателей до и после проведения опытной работы, позволяет сделать следующие выводы: после применения дифференциации на уроках в группе повысился уровень знаний, умений и навыков обучающихся; возрос уровень обученности а, следовательно, и уровень познавательного интереса.

Наиболее заметное влияние дифференциация обучения оказала на уровень обученности обучающихся. Работа каждого учащегося на посильном для него уровне трудности привела к тому, что часть учащиеся, отнесенная нами до проведения дифференциации в группу с низким уровнем обученности, перешли теперь в группу со средним уровнем обученности. Кроме того, повысилось количество обучающихся, чей уровень знаний и умений можно определить как высокий.

Уровень обучаемости в учебном коллективе значительно изменился, в лучшую сторону: три обучающихся перешли в группу высокого уровня - оба из группы среднего уровня обучаемости, тринадцать – из группы низкого уровня в группу среднего уровня обучаемости. В целом, в группе увеличилось число обучающихся, способных самостоятельно или при небольшой помощи преподавателя проработать новый учебный материал, найти алгоритм решения новой задачи. 

Изменение уровня познавательного интереса выразилось  в том, что большая часть обучающихся группы стала с большим желанием решать сложные задачи, преодолевать трудности, с увлечением самостоятельно работать. Количественный состав обучающихся с высоким  и средним уровнем познавательного интереса составил 78,6%.

На основе вышесказанного можно сделать вывод, что дифференцированное обучение, используемое на уроках математики, с учащимися второго курса способствовало повышению эффективности процесса обучения.

Заключение

Исследование дифференциации в обучении математике показало, что изучение этого вопроса в настоящее время является актуальным.

В ходе работы мы определили, что дифференцированный подход – это такая система обучения, которая ставит своей целью создание оптимальных условий для выявления задатков, развития интересов и способностей, она характеризуется формированием групп обучающихся, сходных по какому-либо комплексу свойств и качеств, среди которых основными являются обученность, обучаемость, познавательный интерес. Тем самым современное обучение предоставляет большие возможности для использования дифференцированного обучения. Число и разнообразие способов реализации дифференцированного подхода в училище зависит от творческой направленности преподавателя, от его педагогического мастерства, от умения работать сразу со всей группой и с каждым учащимся в отдельности.

Опыт работы, в ходе которого были применены на практике некоторые из способов реализации дифференцированного обучения (дифференцированно-групповая работа, индивидуализированная самостоятельная работа), показал положительную динамику в формировании познавательного интереса. В группе повысился уровень знаний, умений и навыков обучающихся; возрос интерес обучающихся к математике (повысились способности обучающихся к глубокому изучению программного материала, то есть, эффективность обучения увеличилась, с использованием дифференцированного обучения на уроках математики).

Итак, цель работы по применению способов дифференцированного обучения и их влияния на формирование познавательного интереса обучающихся достигнута, через реализацию следующих задач:

1)      проведен психолого-педагогический анализ информационных источников по проблеме   дифференциации обучения обучающихся;

2)      реализованы способы дифференцированного обучения обучающихся: дифференцированно-групповая работа, индивидуализированная самостоятельная работа;

3)      сделан анализ опыта работы по дифференцированному обучению обучающихся на дисциплине математика.

 

Библиография

 

1)    Калмыкова З.И. Продуктивное мышление как основа обучаемости. - М.: Педагогика, 1981.-200с.

2)    Косенкова Т.А. Из опыта работы со слабыми учащимися.// Математика в школе.-1991.№2-с.12-13.

3)    Крутецкий В.А. Психология математических способностей.- М.: Просвещение, 1968.-467с.

4)    Рабунский Е.С. Индивидуальный подход в процессе обучения обучающихся.- М.: Педагогика, 1975.-82с.

5)    Сухомлинский В.А. Избранные произведения: в 5 т. – Киев: Радянська школа, 1979-1980.

6)    Тимощук М.Е. О дифференцированной помощи учащимся при решении задач//Математика в школе. 1990. №3.-с.13-15

7)    Унт И.Э. Индивидуализация и дифференциация обучения.- М.:Педагогика, 1990. -191с.

8)    Ушинский К.Д. Сочинения. М.- С.-П: АПН РСФСР,1949.

9)    Чередов И.М. О дифференцированном обучении на уроках.- М.: Просвещение, 1973. - 155с.

10)           Щукина Г.И. Проблемы познавательного интереса в педагогике. - М.: Педагогика, 1971.

11)           Юркина С.Н. О дифференцированном обучении математике.// Математика в школе.-1990, №3.-с.13-14.

12)           Якиманская И.С. Личностно-ориентированное обучение в современной школе. - М.:-Сентябрь,1996.-96с.

13)       Якиманская И.С. Развивающее обучение. – М.: Педагогика, 1999.-144с.

 

 

 

 

 

Приложение 1.

 

Пример применения дифференциации на уроке по теме

 «Таблица первообразных».

 

 Цель урока: научить с помощью таблицы находить общий вид первообразной, закрепить этот навык при решении упражнений.

 

На этом занятии дифференциация используется при изучении нового материала. В начале урока вызываются к доске трое обучающихся сильной группы 1.

Задание: найти первообразные для данных функций:

               1 учащийся:  у=хⁿ

                                y=

               2 учащийся:  y= 

                                 y=sinx

               3 учащийся:  y=cosx

                                 y=

 

В это время с остальными учащимися группы проверяется домашнее задание, а затем устно находится первообразная функции y = k.

Далее проверяется правильность выполненных у доски заданий таким образом: по очереди выходят к доске учащиеся групп 2 и 3, каждый проверяет правильность одной из найденных первообразных, обосновывая свои действия ссылкой на соответствующие определения, правила и т.п.

Затем таблица первообразных заносится в тетради.

Приложение 2.

 

Пример применения дифференциации на уроке по теме

 «Правила нахождения первообразных»..

 

Цель: рассмотреть правила нахождения первообразных и поупражнять обучающихся в их применении.

 

После рассмотрения правил нахождения первообразных учащиеся группы 1 сразу же приступают к решению задач из учебника (Колмогоров А.Н. «Алгебра и начала анализа 11 класс» - № 342(а, в), № 343(а, г), № 344(б, г), № 346(а)).                           С учащимися групп 2 и 3 повторно рассматривается каждое правило и решается пример, иллюстрирующий это правило. Затем группа 2 также приступает к самостоятельному решению задач из учебника, а учащиеся группы 3 по очереди решают номера из учебника у доски, поясняя каждое свое действие.

Задания.

 

Найдите общий вид первообразных для функции f:

 

№ 342.

 

 

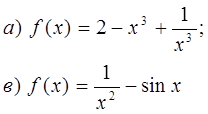
№ 343

 

 

 

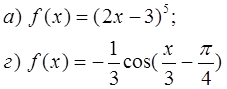
№ 344

 

 

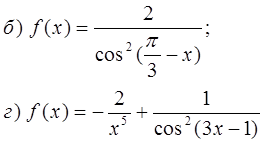
№ 346

 

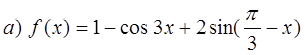
Приложение 3.

 

Пример применения дифференциации на уроке по теме

«Простейшие задачи в координатах» (урок 1).

Цель урока: рассмотреть формулу нахождения координат середины отрезка, нахождения длины вектора по его координатам, нахождения расстояния между двумя точками. Научить обучающихся применять формулы для решения задач.

На этапе закрепления изученного материала проводится дифференцированно-групповая работа (см п.2.2 - пример применения дифференциации на уроке «Правила нахождения первообразных»)

Карточка группы 1.

1.     Середина отрезка АВ лежит на оси Ох. Найдите m и n, если: А (-3; m; 5),                    В (2; -2; n).

2. Точка М – середина отрезка АВ. Найдите координаты точки А, если В (0; 0; 2),     М (-12; 4; 15).

3. Даны точки А(1,5; 1; -2), B (2; 2; -3), C (2; 0; -1). Найдите периметр треугольника АВС и длины его медиан.

Карточка группы 2.

1.                Точка М – середина отрезка АВ. Найдите:

 а) координаты точки М, если А(0; 3; -4), В(-2; 2; 0)

 б) координаты точки В, если А(14; -8; 5), М(3; -2; -7)

2.  Даны векторы  а{5; -1; 7}, b{0; -3; 4}.

Найдите:      а) │a│                       б) │a+ b│

 3. Найдите длину вектора АВ, если А(-35; -17; 20), В(-34; -5; 8).

 

Карточка группы 3.

1.                Точка М – середина отрезка АВ. Найдите координаты точки М, если:

а) А(0; 3; -4), В(-2; 2; 0)                   б) А(1; -2; -4), В(8; 2; 2)

2. Найдите длины векторов          а) а{5; -1; 7}        б) b{0; -3; 4}

3. Найдите длину вектора АВ, если А(-1; 0; 2), В(1; -2; 3).

Приложение 4.

 

Пример применения дифференциации на уроке по теме

«Простейшие задачи в координатах» (урок 2).

Цель урока: закрепить навыки нахождения координат середины отрезка, нахождения длины вектора по его координатам, нахождения расстояния между двумя точками.

После проверки домашнего задания организуется индивидуализированная самостоятельная работа. Каждый учащийся получает карточку, в зависимости от того, в какую группу он входит.

 

Карточка группы 1.

1.   Заданы координаты точек A(-1; 2; 3), B(1; -4; 1), C(1; -3; 2), D(0; 1; 0). Найти расстояние между серединами отрезков АВ и СD.

2.    Найти длины векторов   а = i + j + k,    d = -2k.

3. Точки A(2; 4; -4), B(1; 1; -3), C(-2; 0; 5) являются вершинами параллелограмма ABCD. Найдите координаты точки D.

                                           

Карточка группы 2.

1.     Найти длину вектора (3а - b), если а{2; 3; 2}, b{-1; -2; 1}.

2.     Даны точки А(1; -1; 0), B(1; 2; 3), C(-1; 2; 0). Найти координаты середины отрезка BC и координаты вектора CD, где D - середина отрезка AB.

3. Определите вид треугольника ABC, если A(9; 3; -5), B(2; 10; -5), C(2; 3; 2).

 

Карточка группы 3.

1. Точка М – середина отрезка АВ. Найдите:

 а) координаты точки М, если А(2; -3; -4), В(-3; 1; 0)

 б) координаты точки В, если А(7; 5; 5), М(2; -2; 0)

2. Найдите длину вектора b{; -6; 1}.

3. Определите вид треугольника ABC, если A(3; 7; -4), B(5; -3; 2), C(1; 3; -10).

Приложение 5.

 

Числовой тест.

 

1. Продолжите числовой ряд:                18    20    24    32    …

 

2. Вставьте недостающее число:

 

3. Вставьте недостающее число:

 

 

4. Продолжите числовой ряд:         212    179    146    113   …

 

5. Продолжите числовой ряд:         64    48    40    36    34    …

 

6. Вставьте недостающее число:

 

?	9
81	27

 

2	6
54	18

 

 

7. Вставьте пропущенное число:

 

341                  (250)      466

282                  ( … )      398

 

8. Вставьте пропущенное число:

 

9. Продолжите числовой ряд:          7    19   37    61    …

 

10. Вставьте пропущенное число:          

 

8    5    2

4    2    0

9    6    ?

Приложение 6.

 

Самостоятельная работа.

 

1.        Восстановите пропущенные цифры в записи умножения:

                                   9 5

                                   * *

                                 * * 5

                                 * *

                              * * 3 *

 

2.        Найдите сумму целых чисел от 1 до 50 хотя бы двумя способами.

 

3.        Число 64 представлено в виде суммы двух положительных слагаемых так, что сумма их квадратов минимальна. Найдите эти слагаемые.

Приложение 7.

 

Самостоятельная работа по алгебре.

 

1.                Докажите, что функция F является первообразной для функции f на множестве R:

а) F(x) = x⁴ - 3,       f(x) = 4x³;

б) F(x) = 5x – cos x,     f(x) = 5 + sin x;

 

2. Найдите общий вид первообразной для функции  .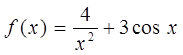

 

3. Для функции найдите первообразную, график которой проходит через     точку М:   .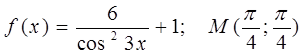

Приложение 8.

 

Самостоятельная работа по геометрии.

 

1.     Даны точки A(2; 7; 1), B(0; -1; 3), B(2; 9; 1) и вектор a{-3; 4; 0}.

         Найти:   а) координаты точки С – середины отрезка АВ.

             б) │AB│

             в) │а│

 

2. Даны точки A(2; 4; -4), B(1; 1; -3), C(-2; 0; 5), D(-1; 3; 4).

Докажите, что они являются вершинами параллелограмма.

 

3. Найдите расстояние от точки A(-1; -7; 0) до плоскости ХОZ.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Скачано с www.znanio.ru