Формирование умения решать задачи с пропорциональными величинами. Ознакомление с содержанием задачи

Формирование умения решать задачи с пропорциональными величинами в начальных классах

Ознакомление с содержанием задачи

Начинать знакомство с задачей и ее частями можно с составления задачи. Например, можно предложить учащимся составить задачу про грибы: «Оля и Таня пошли в лес за грибами. Оля нашла 3 белых гриба (положила в корзиночку), Таня — 2 белых гриба (положила в корзиночку)». Устанавливается, что известно («Что мы знаем? » — «У Оли 3 гриба, у Тани 2 гриба») — это условие задачи. Формулируется вопрос за- дачи. («Что можно спросить про грибы?» — «Сколько всего грибов нашли дети? ») Учащиеся повторяют условие и вопрос задачи, затем всю задачу. Потом они отвечают на вопрос: «Как узнать, сколько всего грибов нашли дети?» («Нужно к 3 прибавить 2, получим 5 грибов, 3 + 2=5»). Это решение задачи. Учащиеся повторяют вопрос задачи и отвечают на него. Итак, задача включает следующие составные элементы: условие (3 гриба у Оли и 2 гриба у Тани), вопрос, решение (3 + 2), ответ (5 грибов).

Для лучшего усвоения понятия «задача» и его составных элементов работа проводится следующим образом. Задача разыгрывается по ролям. Один учащийся формулирует условие, другой — вопрос, третий — решение, четвертый — ответ. Затем составляется задача на нахождение остатка.

Следует отметить, что при выборе решения задачи необходимо иллюстрировать условие, а результат должен быть скрыт, чтобы учащиеся выбирали действие для нахождения результата, а не могли находить результат путем пересчета предметов, иллюстрирующих задачную ситуацию. Пересчет — это способ проверки правильности полученного результата.

В практике работы школ многие учителя предлагают учащимся памятку:

1. Известно... .

2. Надо узнать... .

3. Объясняю... .

4. Решаю... .

5. Ответ... .

На данном этапе необходимо предлагать задания, выполнение которых позволяет лучше осознать суть задачи и ее структуру, например выбрать задачу из приведенных ниже текстов:

1. Оля нашла 5 белых грибов, Таня — 3. Всего дети нашли 8 грибов.

2. Два кольца, два конца, в середине гвоздик. Что это?

3. Оля нашла 5 белых грибов, Таня — 3. Сколько всего грибов нашли дети?

При ознакомлении учащихся с содержанием задачи нового типа важно научить читать ее (выделять интонацией данные, искомые и слова, влияющие на выбор действия, соблюдая логические паузы) и переформулировать (пересказывать кратко и ясно содержание задачи, отбросив все лишнее, но сохранив связи и зависимости между величинами). Проведение такой работы требует постановки специальных вопросов по содержанию задачи: о чем говорится в задаче? Что известно в условии задачи? Что требуется найти? Эти вопросы помогают учащимся осознать суть задачи.

Задачную ситуацию можно проиллюстрировать с помощью реальных предметов или предметов их заменяющих (предметное моделирование), например: «На тарелке лежало 3 красных и 2 зеленых яблока. Сколько всего яблок лежало на тарелке?»

Иллюстрация задачи может быть выполнена в виде схематического рисунка, например: 3 красных круга и 2 зеленых; два отрезка длиной 3 см и 2 см.

Предметное моделирование или схематический рисунок помогают осознать суть задачи и обосновать выбор выполняемых действий.

Постепенно предметную иллюстрацию заменяют схематической, которая называется в методической литературе краткой записью. В краткой записи фиксируют основные «опорные» слова, данные и искомые, а также некоторые слова, влияющие на выбор действия и указывающие на отношения между величинами, входящими в задачу.

Покажем на примере различные виды наглядной интерпретации задачи: «Мама купила 3 кг яблок по 30 р. за 1 кг и 2 кг груш по 40 р. за 1 кг. Сколько стоит вся покупка?»

Схематическая краткая запись приведена ниже:

Схематическая запись отражает все данные, искомые и вопрос задачи.

Краткую запись можно представить в виде таблицы (табл. 1). Чтобы записать задачу в виде таблицы, выделяют величины, о которых идет речь в задаче, и фиксируют их в таблице, затем устанавливают и фиксируют данные и искомые. Неизвестные величины обозначают знаком вопроса.

В данной таблице зафиксированы данные и искомые в легко обозримой форме, что помогает лучше осознать содержание задачи, связи и зависимости между входящими в нее величинами.

Таблица 1

Краткая запись

 Для осознания сути некоторых задач эффективен чертеж, например: «Из двух пунктов, расстояние между которыми 18 км, одновременно навстречу друг другу вышли два пешехода и встретились через 2 ч. С какой скоростью шел первый, если второй шел со скоростью 5 км/ч?» При выполнении чертежа необходимо отметить пункты отправления, указать направления движения стрелкой, соблюдая отношения: большему расстоянию должен соответствовать отрезок большей длины (рис. 1).

Данный чертеж отражает все связи и зависимости между величинами и облегчает поиск пути решения задачи.

Следует отметить, что наглядная интерпретация более эффективна, если ее выполняют сами учащиеся, сначала под руководством учителя, затем самостоятельно.

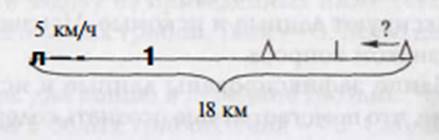
Рис. 1. Чертеж.

Целесообразность использования наглядных средств в процессе обучения решению задач зависит от цели, которая состоит в усвоении как этих наглядных средств, так и знаний, ради которых они используются.

Учитель должен научить учащихся выделять, систематизировать и располагать данные и искомые таким образом, чтобы выполненная наглядная интерпретация задачи помогла обнаруживать скрытые связи между данными и искомыми величинами, входящими в задачу.

Наглядные интерпретации могут быть различными, но требование к ним единственное — они должны помогать учащимся находить путь решения задачи. В противном случае их использование нецелесообразно. В методической литературе [2] отмечается, что с течением времени для многих учащихся, возможно, отпадет необходимость в краткой записи: «Было бы лишней тратой времени требовать ее выполнения и в том случае, если ход решения задачи ясен учащемуся сразу после первого прочтения задачи».

В процессе ознакомления с содержанием задачи и выполнения ее наглядной иллюстрации часть учащихся осознает связи между величинами, входящими в задачу, и может находить путь ее решения. Однако для некоторых учащихся этого недостаточно, чтобы осознать задачную ситуацию и составить план решения. В этом случае учитель проводит беседу, которую в методической литературе называют разбором задачи или поиском пути решения.