Формирование умения решать задачи с пропорциональными величинами. Поиск пути решения задачи

Формирование умения решать задачи с пропорциональными величинами в начальных классах

Поиск пути решения задачи

Правильный и осознанный выбор пути решения задачи обеспечивает метод беседы. Рассуждения можно вести как от вопроса к данным, так и от данных к вопросу. Причем поиск решения можно проводить с опорой на наглядную иллюстрацию (краткая запись, таблица, схематический чертеж или рисунок и т. п.) или по тексту задачи без использования наглядных средств.

Рассмотрим данный метод на примере конкретной задачи: «Для детского сада привезли 4 ящика помидоров по 10 кг в каждом и несколько ящиков огурцов по 8 кг в каждом. Сколько ящиков с огурцами привезли в детский сад, если всего овощей привезли 64 кг?»

Начиная рассуждения от данных, учитель задает вопросы:

О чем говорится в задаче?

Сколько ящиков с помидорами привезли в детский сад?

Какова масса одного ящика?

Что можно узнать по этим данным?

Составляется план решения: «Первым действием находим массу помидоров, вторым — массу огурцов, третьим — количество ящиков с огурцами».

Учитель предлагает учащимся прочитать вопрос и подумать, получен ли ответ на вопрос задачи.

Суть разбора задачи «от данных к вопросу» состоит в следующем: учитель обращает внимание учащихся на два взаимосвязанных числовых данных и ставит вопросы о том, что можно узнать по этим данным и каким действием. Полученный результат (значение величины) сопоставляют с условием задачи, вновь выбирают два взаимосвязанных числовых данных и ставят те же вопросы. И так действуют до тех пор, пока не будет получен ответ на вопрос задачи.

Поиск пути решения можно начинать от вопроса. Учитель задает вопросы:

Каков основной вопрос задачи?

Что нужно знать для ответа на этот вопрос ? (Массу всех огурцов и массу одного ящика с огурцами.)

Что нужно знать, чтобы найти массу огурцов? (Общую массу овощей и массу помидоров.)

Что нужно знать, чтобы найти массу помидоров? (Массу одного ящика с помидорами и число ящиков, а это мы знаем.)

Составляется план решения задачи.

Если поиск решения по тексту задачи вызывает затруднения у учащихся, то можно использовать краткую запись условия задачи или запись в виде таблицы. Учитель может направлять выполнение краткой записи вопросами:

О каких величинах идет речь в задаче? (Отметим в таблице.)

О чем говорится в задаче?

Какие овощи привезли в детский сад? (Огурцы и помидоры — отмечается в таблице.)

Какова масса одного ящика с помидорами? (10 кг — отмечается в таблице.)

Сколько таких ящиков привезли? (4 — фиксируется в таблице.)

Известна ли масса помидоров? (Нет — отмечается в таблице знаком вопроса.)

Какова масса одного ящика с огурцами? (8 кг — отмечается в таблице.)

Известно ли, сколько таких ящиков привезли? (Нет — отмечается в таблице знаком вопроса.)

Какова масса огурцов? (Неизвестно, отмечается знаком вопроса.)

Что обозначает число 64? (Массу всех овощей — отмечается в таблице.)

Затем учитель обращает внимание учащихся на основной вопрос задачи и он отмечается в табличной записи задачи.

Данные и искомые задачи представлены в легкообозримой форме, что облегчает поиск решения задачи. Таким образом, в краткой записи зафиксированы все задачные ситуации, все данные и искомые, основной вопрос задачи. Подобную наглядную интерпретацию в методической литературе называют вспомогательной моделью задачи.

Итак, суть поиска решения задачи при рассуждении «от вопроса» состоит в том, что обращается внимание на основной вопрос задачи и устанавливается, какие значения взаимосвязанных величин необходимы для ответа на данный вопрос. Затем устанавливается, какое значение величины неизвестно и какие 2 величины необходимы для того, чтобы найти эту неизвестную величину. Такие рассуждения проводятся до тех пор, пока не дойдут до данных, необходимых для ответа на поставленный вопрос. План решения составляется в рассуждениях, противоположных направлению разбора задачи.

Рассуждения «от данных к вопросу» называют синтетическим способом разбора (поиском пути решения) задачи (рис. 2, a), a рассуждения «от вопроса» — аналитическим способом разбора (см. рис. 2, б). Возникает вопрос: какому способу отдавать предпочтение?

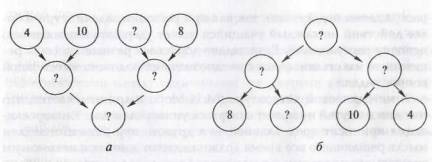
Рис. 2. Рассуждения

Рассуждения.

Некоторые учителя отдают предпочтение разбору задачи, который начинается с вопроса. Они считают, что этот способ наиболее четко направлен на составление плана решения задачи, при этом учащиеся получают представление о решении задачи в целом, а не об отдельно выбранных действиях.

Другие отдают предпочтение разбору задачи от данных к вопросу, полагая, что этот способ разбора доступен и понятен учащимся, у которых вырабатывается умение предвидеть, что можно узнать по данным в условии задачи. При этом легко направить мысль учащегося в нужное русло.

Нужно сказать, что правы и те и другие, поскольку они ориентируются на положительные стороны каждого из рассматриваемых способов поиска решения задачи. Но нельзя забывать и о недостатках каждого способа. Так, при разборе «от данных к вопросу» нередко приходится сталкиваться с неоднозначностью ответа на вопрос задачи. Например, зная, что масса арбуза — 6 кг, а масса дыни — 2 кг, можно найти:

а) какова масса арбуза и дыни;

б) на сколько больше масса арбуза, чем масса дыни;

в) на сколько меньше масса дыни, чем масса арбуза;

г) во сколько раз масса арбуза больше, чем масса дыни;

е) во сколько раз масса дыни меньше, чем масса арбуза.

Следует отметить, что рассуждение «от вопроса к данным» требует более высокого уровня мышления, и для многих учащихся эти рассуждения недоступны, так как при решении задачи в три и более действий не каждый учащийся может удержать в памяти всю цепочку рассуждений. Если задача допускает разные способы решения, то мы сталкиваемся с неоднозначностью ответа на основной вопрос задачи.

В методической литературе (М.И.Моро и др.) отмечается, что ни один из путей не может считаться универсальным. Универсализация приносит вред. Главное — в другом, при решении задачи мысль решающего все время должна идти от данных к искомому и от искомого к данным — только такое встречное движение в обоих направлениях и делает разбор задачи целенаправленным.

При разборе задачи любым способом нельзя упускать из виду основной вопрос. Если установлено, что сразу на вопрос задачи ответить нельзя, то нужно выяснить, что необходимо найти для ответа на вопрос и что можно найти сразу по данным задачи.

Начав рассуждения с вопроса, следует обратиться к данным, а при рассуждениях «от данных» ориентироваться на основной вопрос задачи. Следует отметить, что особенности разбора зависят от структуры задачи, особенностей мышления, уровня подготовки и развития учащихся; это требует от учителя продуманного подхода к выбору способа разбора задачи.