
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Данный фонд оценочных средств составлен на основе:
- Закона РФ от 29.12.2012 г. № 273 - ФЗ «Об образовании»;
- Федеральных государственных образовательных стандартов;
- Федеральных государственных образовательных стандартов основного общего образования (далее – ФГОС ООО);
- Устава МБОУ «СОШ № 6» г. Грозного
- Положения о проведении промежуточной аттестации учащихся и осуществлении текущего контроля их успеваемости.
- Положения о фонде оценочных средств для проведения текущего контроля успеваемости и промежуточной аттестации обучающихся в МБОУ «СОШ № 6» г. Грозного (далее – Положение)
ФОС по предмету, курсу, дисциплине является неотъемлемой частью нормативно-методического обеспечения системы оценки качества освоения учащимися основной образовательной программы ООО, и обеспечивает повышение качества образовательного процесса школы.
ФОС по предмету, курсу, дисциплинепредставляет собой совокупность контрольных материалов, предназначенных для измерения уровня достижения учащимися установленных результатов обучения.
ФОС по предмету, курсу, дисциплине используется при проведении текущего контроля успеваемости и промежуточной аттестации учащихся.
Целями разработки и использования базы ФОС являются:
- оценка качества образования по учебному предмету;
- обеспечение сопоставимости образовательных достижений учащихся в зависимости от условий образовательного процесса;
- подготовка учащихся к процедурам ОГЭ, ГВЭ и ЕГЭ;
- выявление пробелов в знаниях учащихся и своевременная корректировка их индивидуального обучения;
- определение эффективности организации образовательного процесса в школе.
ФОС рассматривается на заседании методического объединения учителей математики и информатики, согласовывается с заместителем директора по учебной части и утверждается директором.
ФОС- сформирован из материалов сборников, допущенных Министерством образования и науки Российской Федерации, а также материалов, разработанных учителем на основе этих сборников.
Данные ФОС составлены на основе:
Контрольные работы 7 класс
Всего контрольных работ: 7
Контрольная работа № 1 по теме «Преобразование выражений»
Вариант 1
1. Найдите
значение выражения 6х – 8у при x = ![]() , y =
, y = ![]() .
.
2. Сравните значения выражений –0,8х – 1 и 0,8х – 1 при х = 6.
3. Упростите выражение.
а) 2х – 3у – 11х + 8у;
б) 5(2а + 1) – 3;
в) 14х – (х – 1) + (2х + 6).
4. Упростите выражение и найдите его значение.
–4 (2,5a –
1,5) + 5,5a – 8 при a = –![]() .
.
5. Из двух городов, расстояние между которыми s км, одновременно навстречу друг другу выехали легковой автомобиль и грузовик и встретились через t ч. Скорость легкового автомобиля υ км/ч. Найдите скорость грузовика. Ответьте на вопрос задачи, если s = 200, t = 2, υ = 60.
6. Раскройте скобки: 3x – (5x – (3x – 1)).
Вариант 2
1. Найдите
значение выражения 16а + 2у при a = ![]() , y =
, y = ![]() .
.
2. Сравните значения выражений 2 + 0,3а и 2 – 0,3а при а = –9.
3. Упростите выражение.
а) 5a + 7b – 2a – 8b;
б) 3 (4х + 2) – 5;
в) 20b – (b – 3) + (3b – 10).
4. Упростите выражение и найдите его значение.
–6 (0,5x – 1,5) – 4,5x
– 8 при x = ![]() .
.
5. Из двух городов одновременно навстречу друг другу выехали автомобиль и мотоцикл и встретились через t ч. Найдите расстояние между городами, если скорость автомобиля υ1 км/ч, а скорость мотоцикла υ2 км/ч. Ответьте на вопрос задачи, если t = 3, υ1 = 80, υ2 = 60.
6. Раскройте скобки: 2p – (3p – (2p – c)).
Решение заданий контрольной работы
Вариант 1
1. Если x =
![]() , y
=
, y
= ![]() ,
то 6x – 8y = 6 ·
,
то 6x – 8y = 6 · ![]() – 8 ·
– 8 · ![]() = 4 – 5 = –1.
= 4 – 5 = –1.
Ответ: –1.
2. Если х = 6, то –0,8х – 1 = –0,8 · 6 – 1 = –4,8 – 1 = –5,8;
0,8х – 1 = 0,8 · 6 – 1 = 4,8 – 1 =3,8.
–5,8 < 3,8, значит, –0,8х – 1 < 0,8х – 1 при х = 6.
Ответ: –0,8х – 1 < 0,8х – 1 при х = 6.
3. а) 2x – 3y – 11x + 8y = (2 – 11) x + (–3 + 8) y = –9x + 5y;
б) 5 (2а + 1) – 3 = 10а + 5 – 3 = 10а + 2;
в) 14x – (x – 1) +
(2x + 6) = 14x – x + 1 + 2x + 6 = (14 – 1 + 2) x
+
+ (1 + 6) = 15x + 7.
Ответ: а) –9х + 5у; б) 10а + 2; в) 15х + 7.
4.
–4 (2,5a – 1,5) + 5,5a – 8 = –10a + 6 + 5,5a – 8 =
(–10 + 5,5) a +
+ (6 – 8) = –4,5a – 2.
Если a = ![]() ,
то
–4,5 ·
,
то
–4,5 · ![]() –
2 = 1 – 2 = –1.
–
2 = 1 – 2 = –1.
Ответ: –1.
5.
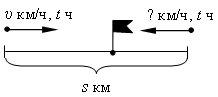
Автомобиль проехал υ · t км, значит, грузовик проехал (s – υ · t) км. Скорость грузовика равна (s – υ · t) : t км /ч.
Если s = 200, t = 2,
υ = 60, то (s – υ
· t) : t = (200 – 60 · 2) : 2 =
= 80 : 2 = 40.
Ответ: 40 км/ч.
6. 3x – (5x
– (3x – 1)) = 3x – (5x – 3x + 1) = 3x – 5x
+ 3x – 1 =
= (3 – 5 + 3) x – 1 = x – 1.
Ответ: х – 1.
Вариант 2
1. Если a =
![]() , y
=
, y
= ![]() ,
то 16а + 2у = 16 ·
,
то 16а + 2у = 16 · ![]() + 2 ·
+ 2 · 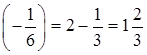 .
.
Ответ: 1![]() .
.
2. Если а = –9, то 2 + 0,3а = 2 + 0,3 · (–9) = 2 – 2,7 = –0,7;
2 – 0,3а = 2 – 0,3 · (–9) = 2 + 2,7 = 4,7.
–0,7 < 4,7, значит, 2 + 0,3а < 2 – 0,3а при а = –9.
Ответ: 2 + 0,3а < 2 – 0,3а при а = –9.
3. а) 5a + 7b – 2a – 8b = (5 – 2) a + (7 – 8) b = 3a – b;
б) 3 (4х + 2) – 5 = 12х + 6 – 5 = 12х + 1;
в)
20b – (b – 3) + (3b – 10) = 20b – b + 3 + 3b
– 10 = (20 – 1 + 3) b +
+ (3 – 10) = 22b – 7.
Ответ: 3а – b; б) 12х + 1; в) 22b – 7.
4. –6 (0,5x
– 1,5) – 4,5x – 8 = –3x + 9 – 4,5x – 8 = (–3 – 4,5) x
+ (9 – 8) =
= –7,5x + 1.
Если x = ![]() , то
, то ![]()
Ответ: –4.
5.
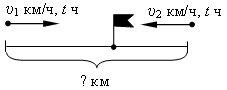
Автомобиль проехал υ1 · t км, мотоцикл – υ2 · t км, значит, расстояние между городами равно υ1t + υ2t км.
Если t = 3,
υ1
= 80, υ2
= 60, то υ1t
+ υ2t
= 80 · 3 + 60 · 3 = (80 + 60) · 3 =
= 140 · 3 = 420 км.
Ответ: 420 км.
6. 2p – (3p
– (2p – c)) = 2p – (3p – 2p + c) = 2p
– 3p + 2p – c =
= (2 – 3 + 2) p – c = p – c.
Ответ: р – с.
Контрольная работа №2 по теме «Уравнения с одной переменной».
Вариант 1
1. Решите уравнение.
а) ![]() x = 12; в)
5x – 4,5 = 3x + 2,5;
x = 12; в)
5x – 4,5 = 3x + 2,5;
б) 6x – 10,2 = 0; г) 2x – (6x – 5) = 45.
2. Таня в школу сначала едет на автобусе, а потом идет пешком. Вся дорога у неё занимает 26 мин. Идет она на 6 мин дольше, чем едет на автобусе. Сколько минут она едет на автобусе?
3. В двух сараях сложено сено, причем в первом сарае сена в 3 раза больше, чем во втором. После того как из первого сарая увезли 20 т сена, а во второй привезли 10 т, в обоих сараях сена стало поровну. Сколько всего тонн сена было в двух сараях первоначально?
4. Решите уравнение 7x – (x + 3) = 3(2x – 1).
Вариант 2
1. Решите уравнение.
а) ![]() x = 18; в)
6x – 0,8 = 3x + 2,2;
x = 18; в)
6x – 0,8 = 3x + 2,2;
б) 7x + 11,9 = 0; г) 5x – (7x + 7) = 9.
2. Часть пути в 600 км турист пролетел на самолете, а часть проехал на автобусе. На самолете он проделал путь в 9 раз больший, чем на автобусе. Сколько километров турист проехал на автобусе?
3. На одном участке было в 5 раз больше саженцев смородины, чем на другом. После того как с первого участка увезли 50 саженцев, а на второй посадили еще 90, на обоих участках саженцев стало поровну. Сколько всего саженцев было на двух участках первоначально?
4. Решите уравнение 6x – (2x – 5) = 2(2x + 4).
Решения заданий контрольной работы
Вариант 1
1.
а) ![]() x
= 12; | · 3 б) 6x – 10,2 = 0;
x
= 12; | · 3 б) 6x – 10,2 = 0;
х = 12 · 3; 6х = 10,2; | : 6
х = 36. х = 1,7.
в) 5x – 4,5 = 3x + 2,5; г) 2x – (6x – 5) = 45;
5x – 3x = 2,5 + 4,5; 2x – 6x + 5 = 45;
2х = 7; 2x – 6x = 45 – 5;
х = 3,5. –4х = 40;
х = –10.
Ответ: а) 36; б) 1,7; в) 3,5; г) –10.
2. Анализ условия:
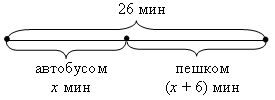
Пусть Таня едет на автобусе х мин, тогда пешком она идет (х + 6) мин. Зная, что вся дорога занимает 26 минут, составим уравнение:
х + (х + 6) = 26;
х + х + 6 = 26;
х + х = 26 – 6;
2х = 20;
х = 10.
Значит, на автобусе Таня едет 10 минут.
Ответ: 10 мин.
3. Анализ условия:
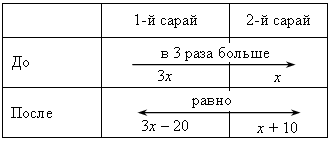
Пусть во втором сарае было х т сена, тогда в первом сарае было 3х т сена. После того как из первого сарая вывезли 20 т сена, там осталось (3х – 20) т сена, а после того как во второй сарай довезли 10 т сена, там стало (х + 10) т. Зная, что после этого сена в обоих сараях стало поровну, составим уравнение:
3х – 20 = х + 10;
3х – х = 10 + 20;
2х = 30;
х = 15.
Значит, во втором сарае первоначально было 15 т сена.
Так как 3х = 3 · 15 = 45, то в первом сарае было 45 т сена.
Следовательно, всего в двух сараях первоначально было 15 + 45, то есть 60 т сена.
Ответ: 60 т.
4. 7x – (x + 3) = 3(2x – 1);
7x – x – 3 = 6x – 3;
7x – x – 6x = –3 + 3;
0 · х = 0;
х – любое число.
Ответ: х – любое число.
Контрольная работа № 3 по теме « Функции».
Вариант 1
1. Функция задана формулой у = 6х + 19. Определите:
а) значение у, если х = 0,5;
б) значение х, при котором у = 1;
в) проходит ли график функции через точку А (–2; 7).
2. а) Постройте график функции у = 2х – 4.
б) Укажите с помощью графика, чему равно значение у при х = 1,5.
3. В одной и той же системе координат постройте графики функций:
а) у = –2х; б) у = 3.
4. Найдите
координаты точки пересечения графиков функций
у = 47х – 37 и у = –13х + 23.
5. Задайте формулой линейную функцию, график которой параллелен прямой у = 3х – 7 и проходит через начало координат.
Вариант 2
1. Функция задана формулой у = 4х – 30. Определите:
а) значение у, если х = –2,5;
б) значение х, при котором у = –6;
в) проходит ли график функции через точку В (7; –3).
2. а) Постройте график функции у = –3х + 3.
б) Укажите с помощью графика, при каком значении х значение у равно 6.
3. В одной и той же системе координат постройте графики функций:
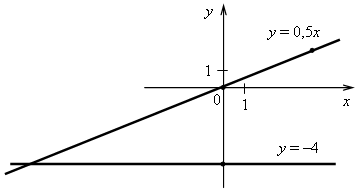
а) у = 0,5х; б) у = –4.
4. Найдите
координаты точки пересечения графиков функций
у = –38х + 15 и у = –21х – 36.
5. Задайте формулой линейную функцию, график которой параллелен прямой у = –5х + 8 и проходит через начало координат
Решение заданий контрольной работы
Вариант 1
1. у = 6х + 19.
а) Если х = 0,5, то у = 6 · 0,5 + 19 = 3 + 19 = 22;
б) если у = 1, то 6х + 19 = 1;
6х = 1 – 19;
6х = –18;
х = –18 : 6;
х = –3;
в) 7 = 6 · (–2) + 19;
7 = –12 + 19;
7 = 7 – верно, значит, график
функции проходит через точку
А (–2; 7).
Ответ: а) 22; б) –3; в) проходит.
|
2. а) у = 2х – 4. Построим две точки, принадлежащие графику. Если х = 0, то у = 2 · 0 – 4 = –4; если х = 2, то у = 2 · 2 – 4 = 0. (0; –4), (2; 0). б) При х = 1,5 у = –1. |
|
|
3. а) у = –2х. Графиком является прямая, проходящая через начало координат и точку (2; –4). б) у = 3. Графиком является прямая, проходящая через точку (0; 3) и параллельная оси х.
4. Решим уравнение: 47х – 37 = –13х + 23. 47х + 13х = 23 + 37; |
|
60х = 60;
х = 1, значит, абсцисса точки пересечения графиков функций равна 1. Найдем соответствующее значение ординаты:
если х = 1, то у = 47 · 1 – 37 = 10.
Точка пересечения имеет координаты (1; 10).
Ответ: (1; 10).
5. График параллелен прямой у = 3х – 7, значит, угловые коэффициенты равны. Так как прямая проходит через начало координат, то это прямая пропорциональность. Значит, у = 3х.
Ответ: у = 3х.
Вариант 2
1. у = 4х – 30.
а) Если х = –2,5, то у = 4 · (–2,5) – 30 = –10 – 30 = –40;
б) если у = –6, то 4х – 30 = –6;
4х = –6 + 30;
4х = 24;
х = 24 : 4;
х = 6;
в) –3 = 4 · 7 – 30;
–3 = 28 – 30;
–3 = –2 – неверно, значит, график функции не проходит через точку В (7; –3).
Ответ: а) –40; б) 6; в) не проходит.
|
2. а) у = –3х + 3. Построим две точки, принадлежащие графику. Если х = 0, то у = –3 · 0 + 3 = 3; если х = 2, то у = –3 · 2 + 3 = –3; (0; 3), (2; –3)
б) Если у = 6, то х = –1. |
|
3. а) у = 0,5х. Графиком является прямая, проходящая через начало координат и точку (4; 2).
б) у = –4. Графиком является прямая, проходящая через точку (0; –4) и параллельная оси х.
4. Решим уравнение:
–38х + 15 = –21х – 36;
–38х + 21х = –36 – 15;
–17х = –51;
х = (–51) : (–17);
х = 3, значит, абсцисса точки пересечения графиков функций равна 3.
Найдем соответствующее значение ординаты:
если х = 3, то у = –38 · 3 + 15 = –99.
Точка пересечения имеет координаты (3; –99).
Ответ: (3; –99).
5. График параллелен прямой у = –5х + 8, значит, угловые координаты равны. Так как прямая проходит через начало координат, то это прямая пропорциональность. Значит, у = –5х.
Ответ: у = –5х.
Контрольная работа № 4 по теме « Многочлены».
Вариант 1
1. Выполните умножение.
а) (с + 2) (с – 3); в) (5х – 2у) (4х – у);
б) (2а – 1) (3а + 4); г) (а – 2) (а2 – 3а + 6).
2. Разложите на множители.
а) а (а + 3) – 2 (а + 3); б) ах – ау + 5х – 5у.
3. Упростите выражение –0,1х (2х2 + 6) (5 – 4х2).
4. Представьте многочлен в виде произведения.
а) х2 – ху – 4х + 4у; б) ab – ac – bx + cx + c – b.
5. Из прямоугольного листа фанеры вырезали квадратную пластинку, для чего с одной стороны листа отрезали полосу шириной 2 см, а с другой, соседней, – 3 см. Найдите сторону получившегося квадрата, если известно, что его площадь на 51 см2 меньше площади прямоугольника.
Вариант 2
1. Выполните умножение.
а) (а – 5) (а – 3); в) (3р + 2с) (2р + 4с);
б) (5х + 4) (2х – 1); г) (b – 2) (b2 + 2b – 3).
2. Разложите на множители.
а) x (x – y) + a (x – y); б) 2a – 2b + ca – cb.
3. Упростите выражение 0,5x (4x2 – 1) (5x2 + 2).
4. Представьте многочлен в виде произведения.
а) 2a – ac – 2c + c2; б) bx + by – x – y – ax – ay.
5. Бассейн имеет прямоугольную форму. Одна из его сторон на 6 м больше другой. Он окружен дорожкой, ширина которой 0,5 м. Найдите стороны бассейна, если площадь окружающей его дорожки 15 м2.
Решение заданий контрольной работы
Вариант 1
1. а) (с + 2) (с – 3) = с2 – 3с + 2с – 6 = с2 – с – 6.
б) (2а – 1) (3а + 4) = 6а2 + 8а – 3а – 4 = 6а2 + 5а – 4.
в) (5х – 2у) (4х – у) = 20х2 – 5ху – 8ху + 2у2 = 20х2 – 13ху + 2у2.
г) (а –
2) (а2 – 3а + 6) = а3 – 3а2
+ 6а – 2а2 + 6а – 12 =
= а3 – 5а2 + 12а – 12.
2. а) а (а + 3) – 2 (а + 3) = (а + 3) (а – 2).
б) ах – ау + 5х – 5у = (ах – ау) + (5х – 5у) = а(х – у) + 5(х – у) =
= (х – у) (а + 5).
3. –0,1х (2х2
+ 6) (5 – 4х2) = –0,1х (10х2 – 8х4
+ 30 – 24х2) = –х3 +
+ 0,8х5 – 3х + 2,4х3 = 0,8х5
+ 1,4х3 – 3х.
4. а) х2
– ху – 4х + 4у = (х2 – ху) – (4х
– 4у) = х(х – у) – 4(х – у) =
= (х – у) (х – 4).
б)
ab – ac – bx + cx + c – b = (ab
– ac) – (bx – cx) – (b – c) =
= a (b – c) – x (b – c) – (b –
c) = (b – c) (a – x – 1).
5. Пусть сторона получившегося квадрата равна х см, тогда его площадь равна х2 см2. Стороны прямоугольника равны (х + 2) см и (х + 3) см, значит, его площадь равна (х + 2) (х + 3) см2.

Составим и решим уравнение:
(х + 2) (х + 3) – х2 = 51;
х2 + 3х + 2х + 6 – х2 = 51;
5х = 45;
х = 9.
Ответ: 9 см.
Вариант 2
1. а) (а – 5) (а – 3) = а2 – 3а – 5а + 15 = а2 – 8а + 15.
б) (5х + 4) (2х – 1) = 10х2 – 5х + 8х – 4 = 10х2 + 3х – 4.
в) (3р + 2с) (2р + 4с) = 6p2 + 12cp + 4cp + 8c2 = 6p2 + 16cp + 8c2.
г) (b – 2) (b2 + 2b – 3) = b3 + 2b2 – 3b – 2b2 – 4b + 6 = b3 – 7b + 6.
2. а) x (x – y) + a (x – y) = (x – y) (x + a).
б)
2a – 2b + ca – cb = (2a – 2b) + (ca
– cb) = 2 (a – b) + c (a – b) =
= (a – b) (2 + c).
3.
0,5x (4x2 – 1) (5x2 + 2) = 0,5x
(20x4 + 8x2 – 5x2 – 2) =
10x5 + 4x3 –
– 2,5x3 – x = 10x5 + 1,5x3
– x.
4.
а)
2a – ac – 2c + c2 = (2a – 2c)
– (ac – c2) = 2 (a – c) – c (a
– c) =
= (a – c) (2 – c).
б)
bx + by – x – y – ax – ay = (bx
+ by) – (x + y) – (ax + ay) =
= b (x + y) – (x + y) – a (x +
y) = (x + y) (b – a – 1).
5. Пусть одна сторона бассейна х м, тогда другая его сторона (х + 6) м. Значит, площадь бассейна х (х + 6) м2.
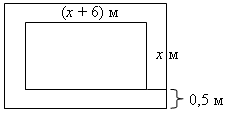
Найдем площадь бассейна вместе с окружающей его дорожкой. Фигура является прямоугольником, стороны которого равны (х + 1) м и (х + 7) м. Значит, площадь прямоугольника равна (х + 1) (х + 7) м2.
Составим и решим уравнение:
(х + 1) (х + 7) – х (х + 6) = 15;
х2 + 7х + х + 7 – х2 – 6х = 15;
2х = 8;
2х = 4.
Ответ: 4 м и 10 м.
Контрольная работа №5 по теме « Формулы сокращенного умножения».
Вариант 1
1. Упростите выражение.
а) (x – 3) (x – 7) – 2x (3x – 5); в) 2 (m + 1)2 – 4m.
б) 4a (a – 2) – (a – 4)2;
2. Разложите на множители.
а) х3 – 9х; б) –5a2 – 10ab – 5b2.
3. Упростите
выражение ![]()
4. Разложите на множители.
а) 16х4 – 81; б) х2 – х – y2 – y.
5. Докажите, что выражение х2 – 4х + 9 при любых значениях х принимает положительные значения.
Вариант 2
1. Упростите выражение.
а) 2х (х – 3) – 3х (х + 5); в) 3 (y + 5)2 – 3y2.
б) (a + 7) (a – 1) + (a – 3)2;
2. Разложите на множители.
а) с3 – 16с; б) 3a2 – 6ab + 3b2.
3. Упростите
выражение ![]()
4. Разложите на множители.
а) 81а4 – 1; б) y2 – х2 – 6х – 9.
5. Докажите, что выражение –а2 + 4а – 9 может принимать лишь отрицательные значения.
Решение заданий контрольной работы
Вариант 1
1. а) ![]()
= –5x2 + 21;
б) ![]()
в) ![]()
= 2m2 + 2.
2. а) х3 – 9х = х (х2 – 9) = х (х – 3) (х + 3);
б) ![]()
3. ![]()
![]()
4. а) 16х4
– 81 = ![]()
× (4x2 + 9);
б) ![]()
= (x + y) (x – y – 1).
5. Выделим из данного трёхчлена квадрат двучлена:
![]()
Выражение (х – 2)2 не может быть отрицательным ни при каких значениях х. Значит, выражение (х – 2)2 + 5 принимает положительные значения при любых х.
Вариант 2
1. а) ![]()
б) ![]()
в) ![]() 75 – 3y2
=
75 – 3y2
=
= 30y + 75.
2. а) с3 – 16с = с (с2 – 16) = с (с – 4) (с + 4);
б) ![]()
3. ![]()
![]()
4. а) 81а4
– 1 = ![]()
б) ![]()
= (y – (x + 3)) (y + (x + 3)) = (y – x
– 3) (y + x + 3).
5. Выделим из данного трёхчлена квадрат двучлена:
![]()
![]()
Выражение –(а – 2)2 не может принимать положительных значений ни при каком значении а. Значит, выражение –(а – 2)2 – 5 может принимать только отрицательные значения.
Контрольная работа № 6 по теме «Системы линейных уравнений».
Вариант 1
1. Решите систему
уравнений: 
2. Банк продал предпринимателю г-ну Разину 8 облигаций по 2000 р. и 3000 р. Сколько облигаций каждого номинала купил г-н Разин, если за все облигации было заплачено 19000 р.?
3. Решите систему
уравнений 
4. Прямая y = kx + b проходит через точки А (3; 8) и В (–4; 1). Напишите уравнение этой прямой.
5. Выясните, имеет
ли решение система и сколько: 
Вариант 2
1. Решите систему
уравнений 
2. Велосипедист ехал 2 ч по лесной дороге и 1 ч по шоссе, всего он проехал 40 км. Скорость его на шоссе была на 4 км/ч больше, чем скорость на лесной дороге. С какой скоростью велосипедист ехал по шоссе и с какой скоростью по лесной дороге?
3. Решите систему
уравнений 
4. Прямая y = kx + b проходит через точки А (5; 0) и В (–2; 21). Напишите уравнение этой прямой.
5. Выясните, имеет
ли решение система и сколько: 
Решение заданий контрольной работы
Вариант 1
1. 
6х – 2(3 – 4х) = 1;
6х – 6 + 8х = 1;
14х = 7;
х = 0,5;
у = 3 – 4 · 0,5;
у = 1.
Ответ: (0,5; 1).
2. Пусть г-н Разин купил х облигаций по 2000 р. и у облигаций по 3000 р.
По условию всего он купил 8 облигаций, то есть получим уравнение: х + у = 8.
За облигации номинала 2000 р. предприниматель заплатил 2000 х р., а за облигации номинала 3000 р. заплатил 3000у р. Всего за облигации было заплачено 19000 р., то есть получим уравнение: 2000х + 3000у = 19000.
Составим и решим систему уравнений:

2000 (8 – у) + 3000у = 19000;
16000 – 2000у + 3000у = 19000;
1000у = 3000;
у = 3;
х = 8 – 3;
х = 5.
Ответ: 5 облигаций по 2000 р. и 3 облигации по 3000 р.
3. 

8 (6 – 2у) + 5у = –7;
48 – 16у + 5у = –7;
–11у = –55;
у = 5;
х = 6 – 2 · 5;
х = –4.
Ответ: (–4; 5).
4. Подставляя координаты точек А и В в уравнение y = kx + b, получим систему уравнений:

–4k + 8 – 3k = 1;
–7k = –7;
k = 1;
b = 8 – 3;
b = 5;
у = х + 5.
Ответ: у = х + 5.
5. Выразим в каждом уравнении системы у через х и сравним коэффициенты k и b:

Так как коэффициенты k равны, а b не равны, то прямые параллельны. Значит, система не имеет решений.
Ответ: не имеет.
Вариант 2
1. 
2х + 3 (3х – 7) = 1;
2х + 9х – 21 = 1;
11х = 22;
х = 2;
у = 3 · 2 – 7;
у = –1.
Ответ: (2; –1).
2. Пусть по лесной дороге велосипедист ехал со скоростью х км/ч, а по шоссейной – со скоростью у км/ч.
На шоссе его скорость была на 4 км/ч больше, поэтому получим уравнение: у – х = 4.
За 2 ч по лесной дороге и 1 ч по шоссе велосипедист проехал (2х + у) км, по условию всего он проехал 40 км. Получим уравнение: 2х + у = 40.
Составим и решим систему уравнений:

3х + 4 = 40;
3х = 36;
х = 12;
у = 4 + 12;
у = 16.
Ответ: 16 км/ч и 12 км/ч.
3. 

2 (5 – 4х) + х = –11;
10 – 8х + х = –11;
–7х = –21;
х = 3;
у = 5 – 4 · 3;
у = –7.
Ответ: (3; –7).
4. Подставляя координаты точек А и В в уравнение y = kx + b, получим систему уравнений:

–7k = 21;
k = –3;
b = –5 · (–3);
b = 15.
Ответ: у = –3х + 15.
5. Выразим в каждом уравнении системы у через х и сравним коэффициенты k и b:

Получили два одинаковых уравнения, значит, система имеет бесконечное множество решений.
Ответ: имеет бесконечное множество решений.
Итоговая контрольная работа №7.
Вариант 1
1. Упростите выражение (a + 6)2 – 2a (3 – 2a).
2. Решите систему
уравнений 
3. а) Постройте график функции y = 2x – 2.
б) Определите, проходит ли график
функции через точку А
(–10; –20).
4. Разложите на множители:
а) 2a4b3 – 2a3b4 + 6a2b2; б) x2 – 3x – 3y – y2.
5. Из пункта А вниз по реке отправился плот. Через 1 ч навстречу ему из пункта В, находящегося в 30 км от А, вышла моторная лодка, которая встретилась с плотом через 2 ч после своего выхода. Найдите собственную скорость лодки, если скорость течения реки 2 км/ч.
Вариант 2
1. Упростите выражение (x – 2)2 – (x – 1) (x + 2).
2. Решите систему
уравнений 
3. а) Постройте график функции y = –2x + 2.
б) Определите, проходит ли график функции через точку А (10; –18).
4. Разложите на множители:
а) 3x3y3 + 3x2y4 – 6xy2; б) 2a + a2 – b2 – 2b.
5. Из поселка на станцию, расстояние между которыми 32 км, выехал велосипедист. Через 0,5 ч навстречу ему со станции выехал мотоциклист и встретил велосипедиста через 0,5 ч после своего выезда. Известно, что скорость мотоциклиста на 28 км/ч больше скорости велосипедиста. Найдите скорость каждого из них.
Решение заданий контрольной работы
Вариант 1
1. (a + 6)2 – 2a (3 – 2a) = a2 + 12a + 36 – 6a + 4a2 = 5a2 + 6a + 36.
2.

5х – 2 (4х – 4) = 11;
5х – 8х + 8 = 11;
–3х = 3;
х = –1;
у = 4 · (–1) – 4;
у = –8.
Ответ: (–1; –8).
|
3. а) График функции y = 2x – 2: б) А (–10; –20): –20 = 2 · (–10) – 2; –20 = –22 – неверно. Ответ: не проходит. |
|
4. а) 2a4b3 – 2a3b4 + 6a2b2 = 2a2b2 (a2b – ab2 + 3);
б) x2
– 3x – 3y – y2 = (x2 – y2)
– (3x + 3y) = (x – y) (x + y) – 3 (x
+ y) =
= (x + y) (x – y – 3).
5. Пусть собственная скорость лодки х км/ч. Выделим процессы: движение плота из пункта А до встречи с лодкой и движение лодки из пункта В до встречи с плотом.
Заполним таблицу:
|
|
s |
υ |
t |
|
плот |
6 км |
2 км/ч |
3 ч |
|
лодка |
2 (х – 2) км |
(х – 2) км/ч |
2 ч |
Составим и решим уравнение:
6 + 2 (х – 2) = 30;
6 + 2х – 4 = 30;
2х = 28;
х = 14.
Ответ: 14 км/ч.
Вариант 2
1. (x – 2)2 – (x – 1) (x + 2) = x2 – 4x + 4 – x2 – 2x + x + 2 = –5x + 6.
2. 
3 (2у – 7) + 5у = 12;
6у – 21 + 5у = 12;
11у = 33;
у = 3;
х = 2 · 3 – 7;
х = –1.
Ответ: (–1; 3).
|
3. а) График функции y = –2x + 2: б) А (10; –18): –18 = –2 · 10 + 2; –18 = –18 – верно. Ответ: проходит. |
|
4. а) 3x3y3 + 3x2y4 – 6xy2 = 3xy2 (x2y + xy2 – 2);
б)
2a + a2 – b2 – 2b = (2a
– 2b) + (a2 – b2) = 2 (a – b)
+
+ (a – b) (a + b) = (a – b) (2 + a
+ b).
5. Пусть скорость велосипедиста х км/ч, тогда скорость мотоциклиста (х + 28) км/ч. Выделим процессы: движение велосипедиста до встречи с мотоциклистом и движение мотоциклиста до встречи с велосипедистом.
Заполним таблицу:
|
|
s |
υ |
t |
|
велосипедист |
х км |
х км/ч |
1 ч |
|
мотоциклист |
0,5 (х + 28) км |
(х + 28) км/ч |
0,5 ч |
Составим и решим уравнение:
х + 0,5 (х + 28) = 32;
х + 0,5х + 14 = 32;
1,5х = 18;
х = 12.
Получаем, что скорость велосипедиста равна 12 км/ч, тогда скорость мотоциклиста равна 12 + 28 = 40 км/ч.
Ответ: 12 км/ч и 40 км/ч.
Критерии оценивания контрольных работ
Текущие контрольные работы имеют целью проверку усвоения изучаемого и проверяемого программного материала. Итоговая контрольная работа проводится в конце учебного года.
Все контрольные работы даны в двух равноценных вариантах. Каждая включает в себя как задания, соответствующие обязательному уровню ( они отмечены знаком ●), так и задания более продвинутого уровня. Их выполнение рассчитано на один урок. Однако следует иметь ввиду, что работы достаточно насыщены по объему. Поэтому учителю необходимо оценить возможности своих учащихся, и если объем работы представляется чрезмерным, то ее следует уменьшить за счет исключения какого-либо из последних заданий. Возможен также и такой вариант, когда одно из заданий работы рассматривается как резервное. Тогда учащимся сообщается, что оценка «5» выставляется в том случае, если правильно выполнены все задания или все задания, кроме одного из последних.
В проверяемых работах учитель отмечает и исправляет допущенные ошибки, руководствуясь следующим:
- учитель только подчеркивает допущенную ошибку, которую исправляет сам ученик;
- подчеркивание ошибок производится учителем только красной пастой (красными чернилами, красным карандашом);
- после анализа ошибок выставляется отметка за работу.
Все контрольные работы обязательно оцениваются учителем с занесением оценок в классный журнал.
При оценке письменных работ учащихся учитель руководствуется соответствующими нормами оценки знаний умений и навыков школьников.
Оценка письменных работ учащихся по математике
Отметка «5» ставится, если:
- работа выполнена верно и полностью;
- в логических рассуждениях и обосновании решения нет пробелов и ошибок;
- решение не содержит неверных математических утверждений (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).
Отметка «4» ставится, если:
- работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
- допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки);
- выполнено без недочетов не менее ¾ заданий.
Отметка «3» ставится, если:
- допущены более одной ошибки или более трех недочетов в выкладках, чертежах или графиках, но учащийся владеет обязательными умениями по проверяемой теме; без недочетов выполнено не менее половины работы.
Отметка «2» ставится, если:
- допущены существенные ошибки, показавшие, что учащийся не владеет обязательными умениями по данной теме в полной мере;
- правильно выполнено менее 2 задание
После проверки письменных работ обучающимся дается задание по исправлению ошибок или выполнению заданий, предупреждающих повторение аналогичных ошибок. Работа над ошибками, как правило, осуществляется в тех же тетрадях, в которых выполнялись соответствующие письменные работы.
Р е к о м е н д а ц и и п о о ц е н и в а н и ю:
Задания 1 и 2 соответствуют уровню обязательной подготовки учащихся.
Для получения отметки «3» достаточно выполнить любые 2 задания. Для получения отметки «5» необходимо решить любые 5 заданий.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.