Фрактальная структура Жюлиа на плоскости H2 как развертка зеркально антисимметричной Сфирали

© О.С. Басаргин

1. Введение

На плоскости двойной переменной H₂ фрактальные множества описываются через итеративный процесс, основанный на квадратичном отображении:

Здесь z_n и c — двойные числа, принадлежащие алгебре H₂, а операция возведения в квадрат и прибавление константы итеративно формируют фрактальную структуру.

В данной работе мы интерпретируем такие структуры через модель Сфирали

— топологически устойчивой фигуры, состоящей из зеркально антисимметричных витков, соединённых S-образным переходом. 2. Визуально-топологическое соответствие

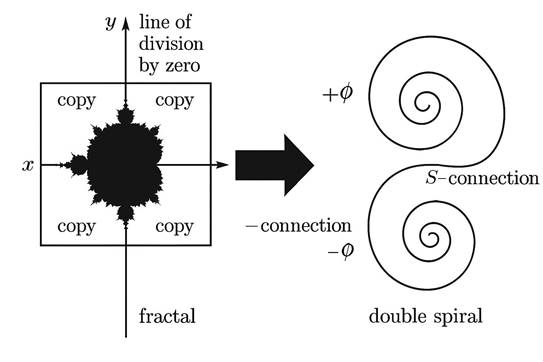
На изображении (см. рис.) представлено сопоставление: слева — фрактал Жюлиа на H₂, справа — соответствующая ему двойная Сфираль.

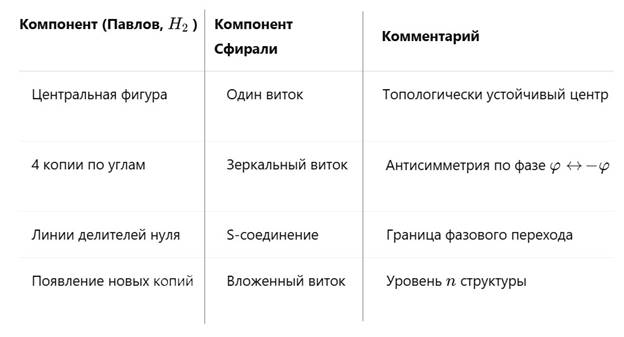
•       Центральная часть фрактала соответствует одному витку.

•       Четыре копии — зеркально-антисимметричному витку.

•       Линии делителей нуля обозначаются условием:

двойного числа

, где z=x  jy.

3. Таблица соответствия

4. Математическая модель витков Пусть каждый виток имеет параметры:

где R_n — радиус витка на уровне n, R₀ — начальный радиус, α  (0,1) — коэффициент масштабирования.

где h_n — вертикальное смещение витка (по оси симметраии), h₀— базовое смещение, β  (0,1) — коэффициент вложенности по высоте.

где φ_n — фазовый угол, который меняет знак на каждом шаге, отражая зеркальную антисимметрию всей конструкции.

5. Заключение

Таким образом, структура предфрактала Жюлиа на H₂ может быть интерпретирована как последовательность вложенных витков зеркальноантисимметричной Сфирали. Это даёт как геометрическое понимание, так и аналитический инструмент описания возникающих фрактальных форм.

Литература 1. Павлов Д.Г., Панчелюга М.С., Панчелюга В.А.

О форме аналогов множества Жюлиа на плоскости двойной переменной. // Гиперкомплексные числа в геометрии и физике. — 2009. — Т.6, №2 (12). — С. 162–176.

2. Басаргин О.С. (2025). Эталонное описание устройства Сфираль. Zenodo. https://doi.org/10.5281/zenodo.15133508