
«Буревестниковская школа»

Выполнил:
ученик 9 «б» класса
Вайсман Артур
Руководитель:
учитель математики
Душухина Юлия Михайловна
п. Буревестник, 2024 год
1.Введение
2. Геометрическое обоснование иллюзий.
2. Виды геометрических иллюзий.
4. Сферы использования геометрических иллюзий.
4.1 Искусство.
4.2 Дизайн одежды.
4.3 Иллюзии в архитектуре.
4.4 Мои геометрические иллюзии.
5. Заключение
6. Источники информации
На уроках геометрии в 7-9 классах мы изучаем признаки и свойства различных плоских фигур. Но в 5 классе мы познакомились и с объёмными фигурами: прямоугольным параллелепипедом и кубом, а в учебнике геометрии 7-9 Л.С.Атанасяна в главе XIV есть начальные сведения о различных многогранниках. Мы делаем чертежи фигур для решения геометрических задач. Но иногда, выполнив чертёж, мы видим ошибочное решение, если опираемся только на зрительное восприятие.
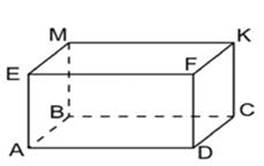
 Например,
если строим прямоугольный параллелепипед, то на чертеже мы видим, что
основаниями являются параллелограммы, но ведь основаниями являются прямоугольники.
По чертежу не всегда можем определить параллельность прямых, это обязательно
надо доказать, используя параллельности прямых.
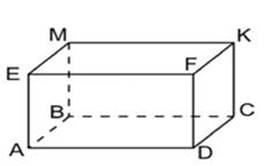
Например,
если строим прямоугольный параллелепипед, то на чертеже мы видим, что
основаниями являются параллелограммы, но ведь основаниями являются прямоугольники.
По чертежу не всегда можем определить параллельность прямых, это обязательно
надо доказать, используя параллельности прямых.
Так же часто с иллюзиями мы встречаемся рассматривая картины. Всегда возникает вопрос: «Как художникам удаётся создать объёмное изображение? Какими методами они пользуются?»
На некоторых картинках вообще нельзя понять, какие изображены прямые (параллельные или нет), какие отрезки (равные или нет).
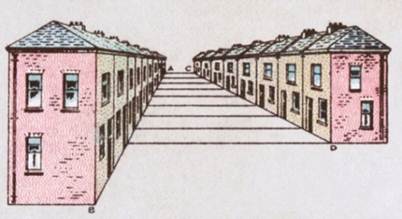
В моём классе я показал одноклассникам несколько рисунков и попросил показать ответить на следующие вопросы
1) Какой из отрезков имеет наибольшую длину, а какой наименьшую?
|
|
|
2) Какая из красных линий длиннее?
|
|
|
3) Какой из отрезков длиннее?
|
|
|
4) Какой круг в центре больше: справа или слева?
|
|
|
5) Какой прямоугольник больше по площади?
|
|
|
6) Какой отрезок длиннее АВ или СD?
|
|
|
7) Какая линия длиннее: вертикальная или горизонтальная?
|
|
8) Какой отрезок длиннее АВ или ВС?
|
|
|
9) Какое изображение куба используют при изучении геометрии и почему?
|
|
|
Ребята отвечали верно, что пунктиром изображают рёбра куба, которые мы не видим.
На примере своих одноклассников я убедился, что зрительные заблуждения человека действительно существуют и связаны они с понятием «иллюзии». Мне захотелось подробнее познакомиться с геометрическими иллюзиями и узнать, в каких сферах жизнедеятельности человека можно с ними столкнуться.
«Иллюзия» в переводе с латинского - это и есть заблуждение, ошибка!
Актуальность темы: в нашем мире
мы часто сталкиваемся с иллюзиями, в том числе и геометрическими.
Проблема: в школьном курсе не изучают геометрические иллюзии, но мы встречаемся с ними при построении чертежей для решения геометрических задач.
Цель работы: познакомиться с геометрическими иллюзиями.
Задачи:
1. изучить теоретический материал по данной теме;
2. убедиться на опыте, что геометрические иллюзии действительно существуют;
3. рассмотреть виды геометрических иллюзий;
4. определить сферы, в которых используют геометрические иллюзии;
5. попробовать самому создать геометрические иллюзии.
Гипотеза: Любую геометрическую иллюзию можно объяснить с помощью математических знаний.
Предмет исследования: геометрические иллюзии;
Объекты исследования: чертежи, картины, фигуры, архитектурные сооружения.
Методы исследования: поиск, изучение, анализ, синтез, анкетирование, эксперимент, обобщение.
Иллюзия - это искажение свойств объекта. Иллюзии с давних времён воспринимались как сбои в работе зрительной системы.
Значит, чтобы разобраться, в природе геометрических иллюзий, надо понять, как человек воспринимает объекты с помощью зрения.
Если мы рассматриваем предмет из различных точек, то видим его под разными углами, т.е угловой размер предмета определён неоднозначно. Его величина зависит от удалённости предмета от глаз. Чем дальше от глаза находится предмет, тем меньше он кажется.
Почему так происходит можно объяснить с помощью геометрических законов.
Пусть h- это высота рассматриваемого предмета, на который сначала смотрели с одного расстояния, а затем с более дальнего.
AB,AC – изображения предмета на сетчатке глаза в обоих случаях соответственно.
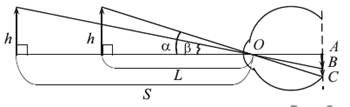
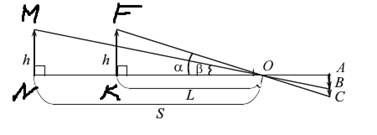
Рассмотрим прямоугольный треугольник NMO : tg b= MN/NO= h/S ;
Рассмотрим прямоугольный треугольник FKO : tg a=FK/KO=h/L;
(tgb)/( tga)=h/S:h/L=L/S;
D ABO : Ð AOB = Ðb (как вертикальные).
tg b= AB/AO
D ACO: ÐAOC=Ða (как вертикальные).
tg a=AC/AO
(tgb)/( tga)= AB/AO:AC/AO=AB/AC;
L/S=AB/AC
Если S=2L, то AC= 2AB, поэтому предмет на расстоянии S будет казаться в два раза меньше, чем на расстоянии L.
Значит, величина угла зрения обратно пропорциональна расстоянию до предмета. Если предмет расположить на расстоянии 1 метр от глаз, а затем его переместить ещё на 1 метр, то он будет казаться в два раза меньше.
Этот факт можно подтвердить экспериментально:
|
|
|
Если предмет расположен очень далеко, то он воспринимается как точка. Существует предельное значение угла зрения, при котором глаз способен видеть раздельно две точки. Поэтому железнодорожные рельсы, деревья аллеи, фонарные столбы кажутся сходящимися в точке на горизонте, а сама точка бесконечно удалённой.
Если наблюдать под одним и тем же углом зрения предметы разного размера, то их размеры будут казаться одинаковыми.
Подтверждением может служить, например солнечное затмение. Во время солнечного затмения Луна целиком закрывает Солнце и их размеры кажутся одинаковыми, потому что оба тела видны с Земли под одним и тем же углом.
Это явление можно объяснить законами геометрии.
|
|
|
AOB : tg a=AB/OB=h/l ; ∆COD: tg a = CD/OD=H/L
h/l=H/L, значит h/H=l/L. Если два предмета видны под одним и тем же углом зрения, то их линейные размеры отличаются во столько же раз, во сколько раз отличаются расстояния до предметов.
1) Иллюзия Мюллера-Лайера(впервые описана в 1889 году)

Отрезки по длине одинаковые, но отрезок в середине кажется длиннее. Есть объяснение, что отрезок со стрелками, направленными наружу, означает угол ближнего объекта, а линия с внутренними стрелками выгляди, как дальний угол комнаты.
|
|
|
|
Но до конца эта иллюзия так и не изучена.
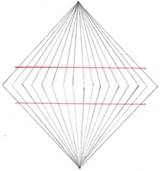 2) Иллюзия
Геринга (обнаружена в 1861 году).
2) Иллюзия
Геринга (обнаружена в 1861 году).
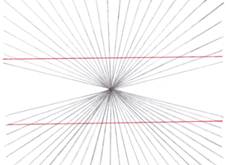
Красные линии параллельны, но мы видим, что они кривые. Это искажение создаётся за счёт фона (пересекающихся линий). Существует и обратная иллюзия. Она называется иллюзия Вундта (описана в 1858 году)
В этом случае красные линии кажутся изогнутыми внутрь.
3) Иллюзия Болдуина.
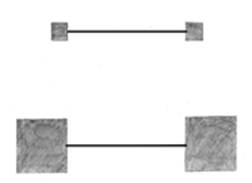
Отрезки между квадратами равны, но на опыте я убедился, что отрезок между малыми квадратами кажется длиннее.
4) Явление иррадации.
Оно состоит в том, что светлые предметы на тёмном фоне кажутся более увеличенными против своих действительных размеров.
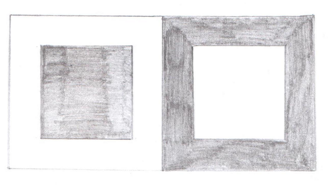
Белый квадрат кажется больше, чем чёрный.
5) Иллюзия Понцо (открыта в 1913 году)

Обе красные линии на рисунке равны по длине, но нам кажется, что верхний отрезок длиннее.
Примером такой иллюзии в природе может быть «лунная иллюзия»
Если Луна находится низко над горизонтом, то она кажется в несколько раз больше, чем высоко в небе.
Я рассмотрел только несколько видов геометрических иллюзий, многие из них открыты несколько сотен лет назад, но не все из них могут точно объяснить даже сейчас.
4.1 Искусство
Многие художники при написании картин используют геометрические иллюзии.
Например, благодаря работам голландского художника М.К. Эшера широкую известность приобрели невозможные фигуры.
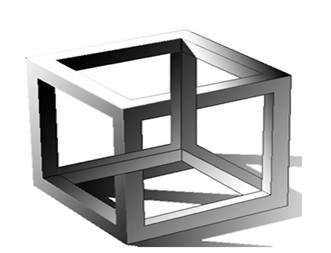
Куб Эшера

Литография «Водопад»
В невозможных фигурах, если внимательно их рассматривать, становятся видны противоречивые соединения элементов фигуры. Создаётся иллюзия невозможности существования в трёхмерном пространстве такой фигуры. Например на фигуре невозможного треугольника основана литография «Водопад» .
Невозможный треугольник был открыт в 1934 году шведским художником Оскаром Реутесвардом. Широкую известность он получил в 1958 году, когда о нём рассказал в своей статье английский физик и математик Роджер Пенроуз, поэтому в дальнейшем его стали называть треугольником Пенроуза.
В книге «Большое , малое и человеческий разум» он показал как можно дать математическое описание этого объекта, исходя из «правил склейки» его деталей.
В Австралии даже существует скульптура невозможного треугольника Пенроуза.

Оскар Реутесвард (шведский художник XX века) изобразил множество невозможных фигур.
Например:
|
|
|
|
Шведским правительством в 1980 году была выпущена серия почтовых марок, на которых были изображены невозможные фигуры Реутесварда
4.2 Дизайн одежды.
Очень часто геометрические иллюзии используют в одежде. Это позволяет
подкорректировать фигуру. Приведу примеры. Вертикальная полоска кажется больше
горизонтальной при равной длине.
Так же используют иллюзию острого угла. С помощью этой иллюзии можно зрительно уменьшить или увеличить необходимую часть тела.
Любые
волнообразные линии на одежде создают иллюзию полноты.
Следующая иллюзия, используемая в дизайне одежды -это иллюзия контраста.
Маленькие формы рядом с большими кажутся ещё меньше.
Так же очень часто используют иллюзию иррадиации, о которой я уже упоминал ранее. Светлые предметы на тёмном фоне кажутся больше.
Конечно, я рассмотрел не все иллюзии, которые применяют при конструировании одежды, но и приведённые примеры показывают, что в этой сфере геометрические иллюзии успешно используют.
4.3 Иллюзии в архитектуре.
Геометрические иллюзии используют в архитектуре. Приведу примеры.

Это здание в Мельбурне (Австралия)

Кривой домик. (Польша)

На этом фото дом дыра в городе Хьюстон. Ещё этот дом называют дом туннель. Строение появилось в 2005 году и просуществовало недолго.
Итак, я убедился, что геометрические иллюзии активно используют в различных сферах деятельности человека и помогают делать жизнь интересной и разнообразной.
4.4 Мои геометрические иллюзии.
Я попробовал создать комнату Эймса, которая широко используется в кино и телевидении. Заготовки для комнаты я взял из журнала «Квантик».
Вот, что у меня получилось
|
|
|
|
|
|
 А
это фото сделано в
А
это фото сделано в
музее иллюзий.
В результате проделанной работы я убедился, что многие иллюзии можно объяснить геометрически, для изображения объёмных фигур на плоскости необходимо пользоваться правилами построения, при решении геометрических задач все выводы необходимо подтверждать с помощью аксиом и теорем геометрии, а не только надеяться на чертёж. Геометрические иллюзии используют во многих сферах деятельности человека, если постараться, то можно самому создать иллюзии и не только геометрические.
1. Вне формата. Занимательная математика: гимнастика для ума или искусство удивлять?- М.: АНО Редакция журнала «Наука и жизнь», 2013.
2. Учебник «Геометрия 7-9»,Л.С. Атанасян,- Просвещение, 2019.
3. Большое, малое и человеческий разум / Роджер Пенроуз,АбнерШимони, Нэнси Картрайт, Стивен Хокинг; [пер. с англ.А. Хачояна под ред. Ю. Данилова]. — СПб.: Амфора. ТИД Амфора, 2008
4. Журнал «Квантик», выпуск №2, февраль 2012 год.( https://kvantik.com/)
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.