Геометрические места точек на плоскости

Геометрические места точек на плоскости

      Геометрическим местом точек называют множество точек, заданное условием, являющимся и свойством, и признаком.

Геометрические места точек

         1.ГМТ, равноудаленных от одной точки, есть поверхность шара с центром в данной точке.

2.ГМТ, равноудаленных от двух точек, есть плоскость, проходящая через середину отрезка, соединяющую данные точки, и к нему перпендикулярная.

3.ГМТ, равноудаленных от трех данных  не лежащих на одной прямой, есть прямая, перпендикулярная к плоскости  и проходящая через центр окружности, описанной около

4.ГМТ, равноудаленных от четырех данных точек, не лежащих в одной плоскости, есть центр шара, поверхность которого проходит через эти точки.

5.ГМТ, равноудаленных от одной прямой, есть поверхность прямого кругового цилиндра, осью которого является данная прямая.

6.ГМТ, равноудаленных от двух параллельных прямых, есть плоскость, перпендикулярная к отрезку, определяющему кратчайшее расстояние между данными прямыми и проходящая через его середину.

7.ГМТ, равноудаленных от двух пересекающихся прямых, есть пара плоскостей, перпендикулярных к плоскости, определяемой данными прямыми и проходящих через биссектрисы углов между ними.

8.ГМТ, равноудаленных от трех параллельных прямых, не лежащих в одной плоскости, есть ось цилиндра, поверхность которого проходит через данные прямые.

9.ГМТ, равноудаленных от трех прямых, проходящих через одну точку, есть ось конуса, поверхность которого проходит через данные прямые.

10.ГМТ, равноудаленных от одной плоскости, есть пара плоскостей, параллельных данной плоскости и расположенных по разные от нее стороны на данном расстоянии.

11.ГМТ, равноудаленных от двух пересекающихся плоскостей, есть две биссекторные плоскости двугранных углов, образованных этими плоскостями.

12.ГМТ, равноудаленных от двух параллельных плоскостей, есть плоскость, параллельная данными и расположенная посредине между ними.

13.ГМТ, равноудаленных от трех плоскостей, проходящих через одну точку, есть ось конуса, вписанного в трехгранный угол, образованный данными плоскостями (если учесть направление плоскостей, то получим четыре прямые).

14.ГМТ, равноудаленных от трех плоскостей, образующих призму (имеющих общую не собственную точку) есть ось цилиндра, вписанного в данную призму (если плоскости продолжить за границу призмы, то получим четыре прямые).

15.Геометрическое место прямых, проходящих через данную точку и наклоненных под углом ɑ к данной плоскости, есть поверхность (прямого кругового) конуса, вершина которого лежит в данной точке, а образующие наклонены под углом ɑ к данной плоскости.

16.ГМТ, из которых данный отрезок виден под данным углом, есть поверхность, полученная от вращения сегмента, опирающегося на данный отрезок и вмещающего данный угол (при ɑ=90 получим поверхность шара).

17.ГМТ, равноудаленных от окружности, есть поверхность тора, осью которого является данная окружность.

18.ГМТ, равноудаленных от двух скрещивающихся прямых, есть поверхность гиперболического параболоида.

Задание с использованием иллюстрации.

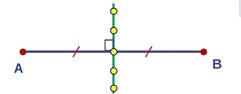
1.     На отрезке АВ найдите геометрическое место точки, равноудаленной от его концов. 

 ответ:

2.     Что представляет собой геометрическое место точек, равноудаленных от концов отрезка?

ответ:

3.     Как выглядит геометрическое место точек, удаленных на расстояние 6 см от точки О?

 ответ: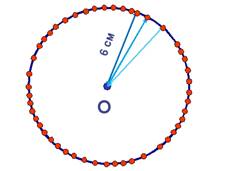

4.     Как выглядит ГМТ, расстояние от которых до заданной точки не больше 6 см?

Ответ: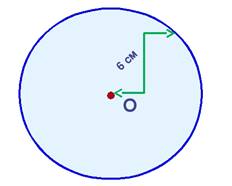

Карточка для письменной работы

Ответьте на вопросы.

1) Что, на ваш взгляд, является геометрическим местом точек, равноудаленным от данной точки?

2) Что будет являться геометрическим местом точек, равноудаленных от сторон угла?

3) Дайте определение геометрического места точек, равноудаленных от концов данного отрезка.

4) Можно ли круг радиуса 5 см считать геометрическим местом точек, удаленных от центра этого круга на расстояние:

А) длиной 5 см;

Б) не больше 5 см;

В) не менее 5 см;

Г) не больше 4 см?

Ответы: Нет Да Нет Нет

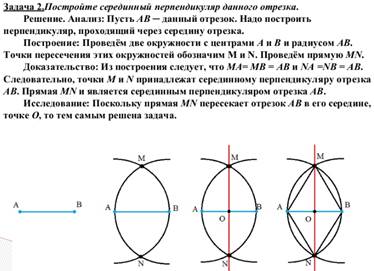
Задачи на распознавание ГМТ:

Скачано с www.znanio.ru