Geometrik shaklni proyeksiyalar tekisligiga parallel o‘q atrofida aylantirish.

Geometrik shaklni proyeksiyalar tekisligiga parallel o‘q atrofida aylantirish.

Umumiy vaziyatda joylashgan tekis geometrik shakllarni proyeksiyalar tekisliklariga parallel bo‘lgan o‘qlar atrofida aylantirib, ba’zi metrik masalalarni yechish mumkin. Bunda, aylanish o‘qi sifatida umumiy vaziyatda joylashgan geometrik shaklning asosiy chiziqlari – gorizontal yoki frontallaridan foydalaniladi. Geometrik shaklni uning gorizontali atrofida aylantirib, H tekislikka parallel vaziyatga, shuningdek, uni frontali atrofida aylantirib, V tekislikka parallel vaziyatga keltirish mumkin.

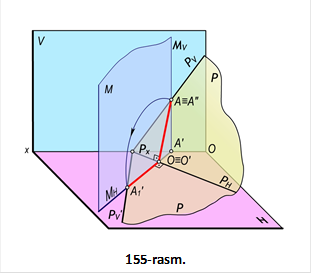
Geometrik shakl proyeksiyalar tekisligiga parallel o‘q atrofida aylantirilganda uning har bir nuqtasi aylanish o‘qiga perpendikulyar bo‘lgan tekislikda aylana bo‘ylab harakatlanadi. Masalan, A nuqtani h gorizontal atrofida aylantirilganda radiusi OA ga teng aylana bo‘yicha M⊥h tekislikda harakatlanadi (152,a–rasm). Bunda, uning gorizontal proyeksiyasi gorizontalning h′ gorizontal proyeksiyasiga perpendikulyar to‘g‘ri chiziq bo‘yicha harakatlanadi.

Chizmada tasvirlangan A(A′, A″) nuqtani A₁(A₁′,A₁″) vaziyatga kelguncha aylantirish uchun aylanish markazi O(O′, O″) nuqtani aniqlash kerak (152,b–rasm). Bu nuqta aylanish o‘qi h ning M tekislik bilan kesishish nuqtasi bo‘ladi. Chizmada aylantirish radiusi R ning haqiqiy o‘lchamni aniqlash uchun H tekislikda to‘g‘ri burchakli ∆O′A′A₀ yasaymiz. Buning uchun AO radiusning A′O′ gorizontal proyeksiyasini to‘g‘ri burchakli uchburchakning bir kateti, OA kesma uchlari applikatalarining ∆z ayirmasini ikkinchi kateti qilib olamiz. Bu uchburchakning gipotenuzasi izlangan aylantirish radiusi R bo‘ladi. A nuqtaning aylantirilgandan keyingi yangi vaziyatining A′₁ gorizontal proyeksiyasi aylanish markazi O′ nuqtada bo‘lgan va O′A₀=R radiusli aylana yoyining M(M_H) tekislikning izi bilan kesishgan  A₁′ nuqtasi bo‘ladi. A nuqtaning yangi A₁″ frontal proyeksiyasi esa h″ to‘g‘ri chiziqda bo‘ladi.

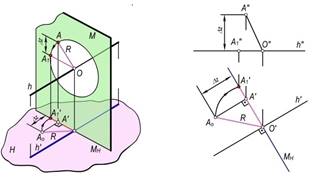
a)                           b)

152-rasm.

1–masala. Umumiy vaziyatdagi ∠ABC(∠A′B′C′,∠A″B″C″) ning haqiqiy o‘lchami aniqlansin (153–rasm).

Echish. Berilgan burchakning gorizontali yoki frontalidan foydalaniladi. Mazkur burchakning haqiqiy o‘lchamini aniqlash uchun chizmada uning f(f′, f″) frontali o‘tkazilgan. Rasmda hosil bo‘lgan ∠ABE(∠A′B′E′, ∠A″B″E″) ning haqiqiy o‘lchamini aniqlash uchun B nuqtani aylantirish radiusining haqiqiy o‘lchamini aniqlash kifoya. Buning uchun B″ nuqtadan f″ ga perpendikulyar o‘tkaziladi va aylanish markazining O_B(O′_B,O″_B), so‘ngra aylantirish radiusining BO_B(B′O′_B, B″O″_B) proyeksiyalari aniqlanadi. To‘g‘ri burchakli ∆O″_BB″B″_O yasash bilan radiusning haqiqiy o‘lchami O″_BB″₁=R aniqlanadi. B nuqtaning yangi vaziyatini yasash uchun O″_B dan R radius bilan O″_BB″₁ perpendikulyarning davomi bilan kesishguncha yoy o‘tkaziladi va hosil bo‘lgan B″₁ bilan A″ va E″ nuqtalarni tutashtiriladi. Chizmada hosil bo‘lgan α berilgan burchakning haqiqiy o‘lchami bo‘ladi.

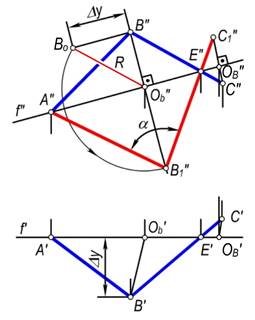
153-rasm.

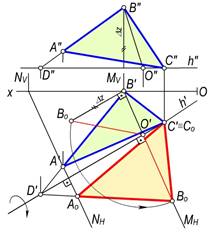
2–masala. Umumiy vaziyatdagi ∆ABC(∆A′B′C′, ∆A″B″C″) ning haqiqiy o‘lchami aniqlansin.

Yechish. Uchburchak gorizontali h(h′, h″) o‘tkaziladi. ∆ABC ning haqiqiy o‘lchamini aniqlash uchun uning B(B′,B″) va C(C′, C″) uchlari aylantirish radiuslarining haqiqiy o‘lchamlari aniqlanadi.

Chizmada B nuqtaning aylantirish radiusini aniqlash uchun uning O′B′ va O″B″ proyeksiyalaridan foydalanib, to‘g‘ri burchakli ∆O′_oB′B′_o ni yasaymiz. Bu uchburchakning O′B′_o gipotenuzasi B nuqtaning aylantirish radiusi bo‘ladi. B nuqtaning yangi vaziyati aylantirish markazining gorizontal proyeksiyasi O′ dan radiusi O′B_o ga teng qilib o‘tkazilgan yoyning harakat tekisligining M_H izi bilan kesishgan B_o nuqtasi bo‘ladi.

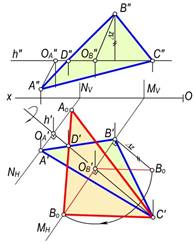
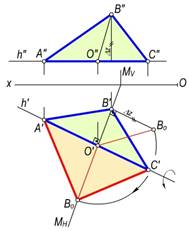
a)                                   b)                                  v)

154-rasm.

Uchburchakning S va D nuqtalari aylanish o‘qiga tegishli bo‘lgani uchun ularning fazoviy vaziyatlari o‘zgarmaydi. Uchburchak A nuqtasi aylantirish radiusining haqiqiy o‘lchamini ham B nuqta aylantirish radiusining haqiqiy o‘lchamini topish kabi aniqlash mumkin. Ammo uchburchakning A nuqtasi h o‘qi atrofida B nuqta kabi harakatlanganda N(N_H) tekislikka va uchburchakning AB tomoniga tegishli bo‘lib qoladi. Uchburchakning AB tomoni esa qo‘zg‘almas D nuqtadan o‘tadi. Shuning uchun chizmada A nuqtaning yangi vaziyatini aniqlash uchun B₀ va D′ nuqtalar o‘zaro tutashtiriladi va A′ nuqtadan C′D′ ga tushirilgan perpendikulyar bilan kesishguncha davom ettirilib, A₀ nuqta topiladi. Agar A₀, B₀ va C′ nuqtalar o‘zaro tutashtirilsa, uchburchakning haqiqiy kattaligi hosil bo‘ladi.

Agar uchburchakning biror tomoni (masalan, AC) gorizontal vaziyatda berilgan bo‘lsa, masala 154,b-rasmda ko‘rsatilgan kabi yechiladi.

154,v-rasmda aylanish o‘qi gorizontal bo‘lib, uchburchak konturidan tashqarida C nuqta orqali o‘tkazilgan. Bu holda uchburchakning haqiqiy kattaligi uning gorizontal proyeksiyasi bilan ustma-ust tushmaydi, natijada, masalaning yechimi yaqqolroq bo‘ladi.[1]

Скачано с www.znanio.ru