
Урок обобщения и систематизации знаний, умений и навыков.
Урок-практикум.
Тема: «Графический метод определения числа корней
уравнений с параметрами, содержащих знак модуля»
Цели:
Познавательная (обучающая): обобщение, углубление уже известного материала на построение графиков функций, содержащих переменную под знаком модуля, и решение уравнений с параметрами.
Развивающая: формирование умений анализировать, сравнивать, обобщать, переносить знания в новые ситуации.
Воспитательная: воспитание личностных качеств, обеспечивающих успешность исполнительской деятельности (трудолюбия, внимательности, аккуратности).
Воспитание личностных качеств, обеспечивающих успешность творческой деятельности (активности, увлечённости, целеустремлённости, наблюдательности, интуиции, сообразительности, самостоятельности).
План урока.
1. Организационный этап.
2. Этап всесторонней проверки ЗУН.
3. Этап подготовки учащихся к активному и сознательному усвоению материала по решению уравнений с параметром и уравнений содержащих переменную под знаком модуля с параметром графическим способом.
4. Этап проверки понимания учащимися материала: использование графического способа решения уравнений с параметрами.
5. Этап закрепления и контроля знаний, навыков учащихся по данной теме.
6. Этап информирования учащихся о домашнем задании, инструктаж о его выполнении.
7. Подведение итогов урока.
Ход урока
1. Организационный этап.
Дидактическая задача: Подготовить учащихся к работе на уроке, определить цели и задачи урока.
Учитель организует учащихся, сообщает тему урока, дату проведения урока, цели и задачи урока.
2. Этап всесторонней проверки ЗУН.
Дидактическая задача: Глубоко и всесторонне проверить знания учащихся по построению графиков функций, содержащих знак модуля и радикала, выявив причины обнаруженных пробелов в знаниях и умениях для их устранения. Стимулировать опрашиваемых и весь класс к овладению традиционными приёмами в построении графиков и графическом решении уравнений.
На данном этапе используем различные методы проверки знаний, начиная от фронтальной беседы, индивидуального опроса. Постановка дополнительных вопросов для проверки прочности и глубины осознанности знаний; создание при опросе нестандартных заданий.
Использование мультимедийного проектора. Тестовое задание на соответствие графиков и их аналитической записи.
На предыдущих двух уроках была отработана методика построения графиков функций, содержащих переменную под знаком модуля.
Определите, какой функции, заданной формулой, соответствует график.
Задание 1
1) у = |х|
а)
2) у = |х+1|
б)
3) у = |х|+1
в)
4) у = |х+1|-1
г)
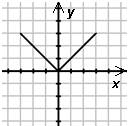
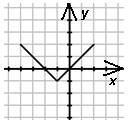
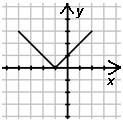
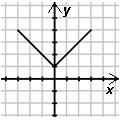
|
Ответ: |
1 |
2 |
3 |
4 |
|
|
а |
в |
г |
б |
Задание 2
1) ![]()
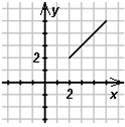
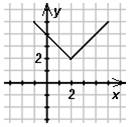
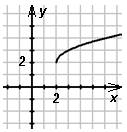 а)
а)
2) ![]()
б)
3) ![]()
в)
О.Д.З. ![]()
![]()
![]()
![]()
О.Д.З.
![]()
x – любое
![]()
![]()
![]()
О.Д.З. ![]()
![]()
(2,2) – вершина графика
![]() – шаблон
– шаблон
|
Ответ: |
1 |
2 |
3 |
|
|
а |
б |
в |
Задание 3
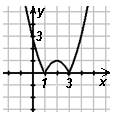
1) у =|x2-4x+3| 2) y= x2 -4|x|+3 3) у=|x2-
y=x2-4x+3
- Найдем абсциссу вершины параболы: у’=2x – 4, y’=0
х=2, у=-1. (2;,-1)
- Найдем точки пересечения с осью Ох: у=0, х2-4х+3=0
![]() x=1 (1;0 )
x=1 (1;0 )
x=3 (3;0)
- Найдем точки пересечения с осью Оу: x=0, y=3 (0;3)
а) б) в)
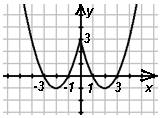
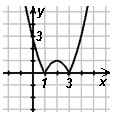
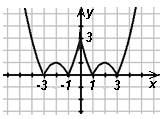
|
Ответ: |
1 |
2 |
3 |
|
|
б |
в |
а |
Задание 4
1)
![]()
2)
![]()
3)
![]()
4)
![]()
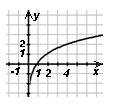
у = log2 x, x>0
а)
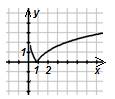
б)
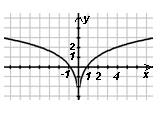 в)
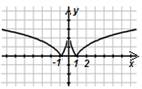
в)
г)
|
Ответ: |
1 |
2 |
3 |
4 |
|
|
а |
в |
б |
г |
Задание 5
1)
![]()
2)
![]()
3)
![]()
а)
График функции
![]() получаем из
графика
получаем из
графика ![]() в результате сдвига вправо на 3
единицы по Ох и вверх на 1 единицу по Оу
в результате сдвига вправо на 3
единицы по Ох и вверх на 1 единицу по Оу
Д(у) = (-¥;3) È (3;+ ¥)
Е(у) = (-¥;1) È (1;+ ¥)
асимптоты х=3; у=1
б)
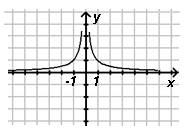
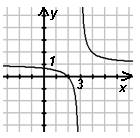
График функции может быть получен из графика ![]() в
результате зеркального отображения относительно оси Оу правой части графика
(левая часть отбрасывается)
в
результате зеркального отображения относительно оси Оу правой части графика
(левая часть отбрасывается)
в) 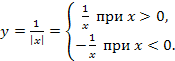
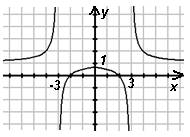
Если х>0, то ветвь гиперболы в I
четверти. При x<0 происходит отображение относительно оси абсцисс
графика ![]() , т.к. графики функций y=f(x) и y=-f(x)
расположены симметрично оси абсцисс
, т.к. графики функций y=f(x) и y=-f(x)
расположены симметрично оси абсцисс
|
Ответ: |
1 |
2 |
3 |
|
|
в |
а |
б |
3. Этап подготовки учащихся к активному и сознательному усвоению материала по решению уравнений с параметром содержащих переменную под знаком модуля графическим способом.
Дидактическая задача: организовать и направить мыслительную деятельность учащихся на решение уравнений с параметром графически. Эти навыки учащиеся смогут применить при решении заданий из ЕГЭ.
Сегодня нам предстоит продолжить наше знакомство с уравнениями с параметрами. На прошлых уроках мы научились решать не только линейные уравнения с параметрами, но и решали дробно-рациональные уравнения, рассматривали задачи, при которых мы прибегали к решению уравнений с параметрами, решали уравнения с параметром под знаком модуля аналитическим способом. И вот сегодня на уроке мы с вами будем решать уравнения с параметрами, содержащие знак модуля, и рассмотрим графический метод решения таких уравнений.
Пример
№ 1: Найдите число корней уравнения ![]() в
зависимости от параметра a.
в
зависимости от параметра a.
Решение:
Построим
график функции ![]() и
и ![]() в одной системе координат.
в одной системе координат.
Уравнение ![]() имеет столько решений, сколько раз прямая
имеет столько решений, сколько раз прямая ![]() пересекает
график функции
пересекает
график функции ![]()
1)
Построим график функции ![]()
Найдём абсциссу вершины параболы с помощью производной:
![]()
![]()
![]()
![]()
точка
![]() с 0х:
с 0х:
![]()
![]()
с 0y: ![]()
2) Построим график функции ![]()
Для того, чтобы построить график функции ![]() ,
если известен график функции
,
если известен график функции ![]() , нужно оставить на месте ту часть, где
, нужно оставить на месте ту часть, где ![]() , и
симметрично отобразить относительно оси х другую его часть, где
, и
симметрично отобразить относительно оси х другую его часть, где ![]()
3) Построим прямую у = a
4)
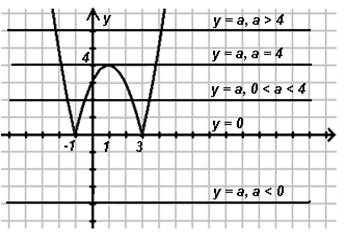 Построение:
Построение:
5) Видно:
1.
если
![]() , то графики не имеют общих точек, т.е.
нет корней;
, то графики не имеют общих точек, т.е.
нет корней;
2.
если
![]() , то графики имеют две общие точки, т.е.
два корня;
, то графики имеют две общие точки, т.е.
два корня;
3.
если
![]() , то графики пересекаются в четырёх
точках, что даёт четыре корня;
, то графики пересекаются в четырёх
точках, что даёт четыре корня;
4.
если ![]() то графики имеют три общие точки, т.е. три корня;
то графики имеют три общие точки, т.е. три корня;
5.
если
![]() то графики имеют две общие точки, т.е. два
корня.
то графики имеют две общие точки, т.е. два
корня.
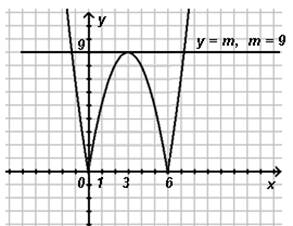
Пример № 2: Найдите значение параметра m,
при котором уравнение ![]() имеет
ровно три корня.
имеет
ровно три корня.
Решение:
Построим график функции ![]() и
и
![]() на
одном чертеже.
на
одном чертеже.
1)
Построим график функции ![]()
Найдем координаты вершины параболы выделением квадрата двучлена
![]()
![]() вершина
параболы
вершина
параболы
![]()
![]()
2)
Построим график функции ![]() .
.
Для
того, чтобы построить график функции ![]() , если известен график
, если известен график ![]() , нужно оставить на месте ту часть, где
, нужно оставить на месте ту часть, где ![]() , и
симметрично отобразить относительно оси х другую его часть, где
, и
симметрично отобразить относительно оси х другую его часть, где ![]() .
.
3) Построим прямую у = m
4)
 Построение:
Построение:
5)
Очевидно, что исходное уравнение
имеет ровно 3 решения тогда и только тогда, когда графики двух вышеуказанных
функций пересекаются ровно в 3-х точках, т.е. при ![]()
Пример
№ 3: Найдите число решений уравнения
![]() в
зависимости от параметра p
в
зависимости от параметра p
Решение:
Построим
график функций ![]() и
и ![]() на одном чертеже.
на одном чертеже.
1)
Построим график функции ![]() ,
найдем абсциссу вершины параболы с помощью производной.
,
найдем абсциссу вершины параболы с помощью производной.
![]()
![]()
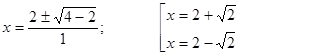
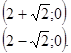
![]()
2)
Построим график функции ![]() .Для
того, чтобы построить график функции
.Для
того, чтобы построить график функции ![]() , нужно оставить на месте ту часть графика функции
, нужно оставить на месте ту часть графика функции ![]() ,
которая соответствует неотрицательной части определения функции
,
которая соответствует неотрицательной части определения функции ![]() .
Отобразив эту часть симметрично относительно оси у, получим другую часть
графика, соответствующую отрицательной области определения.
.
Отобразив эту часть симметрично относительно оси у, получим другую часть
графика, соответствующую отрицательной области определения.
3) Построим прямую у = р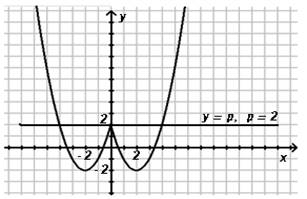
4) Построение:
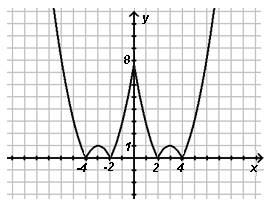
5) Очевидно, что исходное уравнение имеет ровно три корня тогда и только тогда, когда графики пересекаются ровно в 3-х точках, т.е при р = 2.
Пример
№ 4: Определить корни уравнения ![]() в
зависимости от параметра m.
в
зависимости от параметра m.
Решение:
1)
Построим график ![]() .
.
Сделав
необходимые преобразования, получим график функции ![]()
2) Построим прямую у = т
3)
 Построение:
Построение:
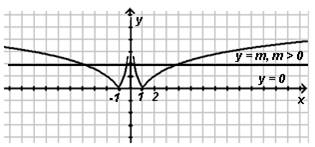
4) Ответ:
а) если m = 0, то 2 решения;
б) если m > 0, то 4 решения.
Пример № 5: Найти значение параметра p, при котором уравнение
![]() имеет
одно решение
имеет
одно решение
Решение:
1)
Преобразуем: ![]()
2)
Построим график функции ![]() получаем
его из графика функции
получаем
его из графика функции ![]() в результате зеркального отображения той части
графика, которая расположена ниже оси х, остальная часть графика не
меняется.
в результате зеркального отображения той части
графика, которая расположена ниже оси х, остальная часть графика не
меняется.
3)
Построим график ![]() асcимптоты
х = -3,
асcимптоты
х = -3,
у = 1.
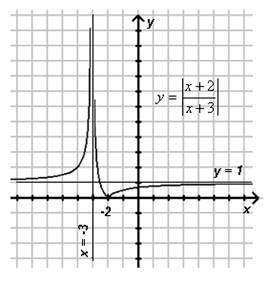
Ответ: а) при p = 0 и p = 1 уравнение имеет одно решение.
4. Этап проверки понимания учащимися материала: использование графического способа решения уравнений с параметрами.
Дидактическая задача: установить, усвоили или нет учащиеся связь между фактами, закономерностями в построении графиков и определении числа корней уравнений.
Работа ведётся у доски 3 учащимися (пример В8 ЕГЭ 2009г.).
Пример
№ 1. При каких значениях параметра ![]() уравнение
уравнение
![]() имеет
имеет
два корня.
Решение:
1) построим
график функции ![]() и
и ![]() на одном чертеже.
на одном чертеже.
2)
Построение: 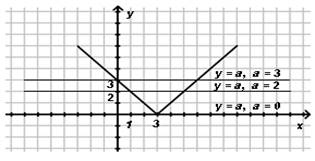
Ответ: а) если а = 0, то 1 решение
б) если а > 0, то 2 решения.
Пример № 2.
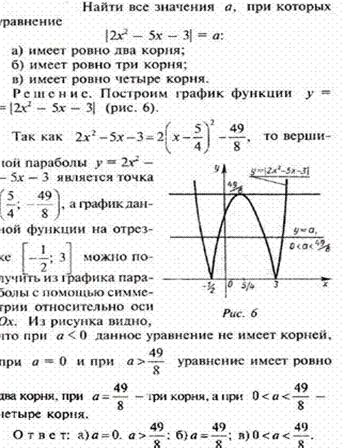
Пример № 3. Найти все значения m, при которых уравнение ![]() имеет
ровно два решения.
имеет
ровно два решения.
Решение:
1) построим
график функции ![]() и
и
![]() на одном чертеже.
на одном чертеже.
![]()
![]()
![]()
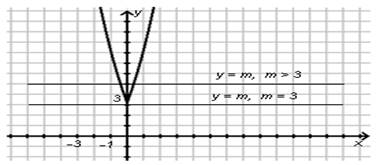
2) Построение:
Ответ: а) если m = 3, то 1 решение; б) m > 3, то 2 решения.
5. Этап закрепления и контроля знаний, навыков учащихся по данной теме.
Дидактическая задача: закрепить у учащихся те знания и умения, которые необходимы для подготовки к ЕГЭ.
Самостоятельная работа (2 варианта) – 20 минут.
|
Вариант 1 |
Вариант 2 |
|
1. При
каком значении
|
1. При
каком значении
|
|
2. При
каком значении
|
2. При
каком значении
|
|
3. При
каком значении
|
3. При
каком значении
|
|
4.
Определить количество корней уравнения, взаимозависимого от параметра
|
4.
Определить количество корней уравнения, взаимозависимого от параметра
|
Решения задач самостоятельной работы приведены в Приложении 1.
6. Этап информирования учащихся о домашнем задании, инструктаж о его выполнении.
Дидактическая задача: сообщить учащимся домашнее задание, разъяснить методику его выполнения и подвести итоги работы.
Учитель поясняет домашнее задание, обращая внимание учащихся на
то, что аналогичные задания были разобраны на доске.
С помощью беседы обсуждается план решения домашнего задания.
Домашнее задание:
Определить количество корней уравнения, в зависимости
от параметра ![]() .
.
1) ![]()
2) 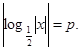
3) ![]()
4) ![]()
Решения задач домашнего задания приведены в Приложении 2.
7. Подведение итогов урока:
Дидактическая задача: проанализировать работу на уроке, дать оценку успешности достижения цели и наметить перспективу на будущее.
Список литературы.
1. 3000 конкурсных задач по математике. / Е.Д. Куланин [и др.] – М.: Рольф, Айрис-пресс, 2000. – 624 с., с илл.
2. Слонимская И.С. Математика. Экспресс-репетитор для подготовки к ЕГЭ. «Уравнения» и «неравенства». / Н.С. Слонимская – М.: АСТ: Астрель, 2009. – 157 с.
3. Родионов Е.М. Математика. Решение задач с параметрами: Пособие для поступающих в вузы. / Е.М. Родионов. – М: Изд-во НЦ ЭНАС, 2006. – 216 с.
4. Гельфанд И.М. Функции и графики (основные приёмы). / И.М. Гельфанд, Е.Г. Глаголева, Э.Э. Шноль. М.: Наука, 1973 – 96 с., с илл.
5. Гурский И.П. Функции и построение графиков. / И.П. Гурский – М.: Просвещение, 1968 – 215 с., с илл.
Приложение 1.
Решения задач самостоятельной работы:
|
Вариант 1 |
Вариант 2 |
|
1. При
каком значении
Решение: Построим
Один корень при |
1. При
каком значении
Решение: Построим
При |
|
2. При
каком значении
Решение: Построим
При |
2. При
каком значении
Решение: Построим
При |
|
3. При
каком значении
Решение:
Построим график:
При |
3. При
каком значении
Решение:
Построим график:
При |
|
4. Определить количество корней
уравнения, в зависимости от параметра
Решение:
Построим график
При При При |
4. Определить количество корней
уравнения, в зависимости от параметра
Решение:
Построим график
При При При |
Приложение 2.
Решение домашнего задания:
1) ![]()
Построим график.
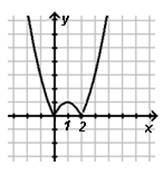
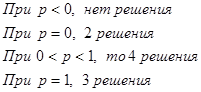
2) 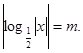
Построим график.
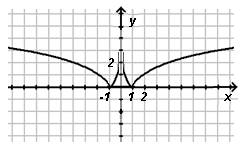
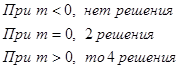
3) ![]()
Построим
график ![]()
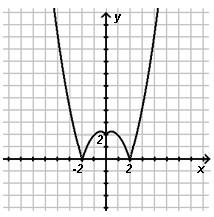
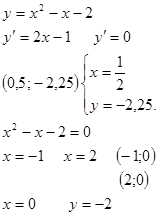

4) ![]()
Построим график.
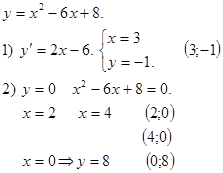
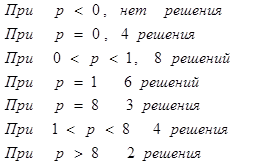
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.