Игровые технологии на уроках русского языка

 Игровые технологии являются одной из уникальных форм обучения, которая позволяет сделать интересными и увлекательными не только работу учащихся на творческо-поисковом уровне, но и будничные шаги по изучению основных предметов начальной школы. Занимательность условного мира игры делает положительно эмоционально окрашенной монотонную деятельность по запоминанию, повторению, закреплению или усвоению информации, а эмоциональность игрового действа активизирует все психические процессы и функции ребенка. Другой положительной стороной игры является то, что она способствует использованию знаний в новой ситуации, т.е. усваиваемый учащимися материал проходит через своеобразную практику, вносит разнообразие и интерес в учебный процесс, способствует формированию информационно-коммуникативных навыков учащихся. Игра — основной вид деятельности ребёнка. С. Л. Рубинштейн (1976) отмечал, что игра хранит и развивает детское в детях, что она их школа жизни и практика развития.

По мнению Д. Б. Эльконина (1978), “в игре не только развиваются или заново формируются отдельные интеллектуальные операции, но и коренным образом изменяется позиция ребёнка в отношении к окружающему миру и формируется механизм возможной смены позиции и координации своей точки зрения с другими возможными точками зрения”.

Игра – особо организованное занятия, требующее напряжения эмоциональных и умственных сил.

Технология (от др.-греч. ????? — искусство, мастерство, умение; ????? — мысль, причина; методика, способ производства) — совокупность методов, процессов и материалов, используемых в какой-либо отрасли деятельности. Технология, в узком смысле, это комплекс организационных мер, операций и приемов, направленных на изготовление, обслуживание, ремонт и/или эксплуатацию изделия с номинальным качеством и оптимальными затратами, и обусловленных текущим уровнем развития науки, техники и общества в целом.

Игровая технология строится как целостное образование, охватывающее определенную часть учебного процесса и объединенное общим содержанием, сюжетом, персонажем. В нее включаются последовательно игры и упражнения, формирующие умение выделять основные, характерные признаки предметов, сравнивать, сопоставлять их; группы игр на обобщение предметов по определенным признакам; группы игр, в процессе которых у младших школьников развивается умение отличать реальные явления от нереальных; группы игр, воспитывающих умение владеть собой, быстроту реакции на слово, фонематический слух, смекалку и др. При этом игровой сюжет развивается параллельно основному содержанию обучения, Игра помогает активизировать учебный процесс, осваивать ряд учебных элементов. Составление игровых технологий из отдельных игр и элементов - забота каждого учителя начальной школы.

Важнейшей задачей современной системы образования является формирование универсальных учебных действий, обеспечивающих школьникам умение учиться, способность к саморазвитию и самосовершенствованию.

В широком значении термин “универсальные учебные действия” означает умение учиться, т. е. способность субъекта к саморазвитию и самосовершенствованию. В более узком (собственно психологическом) значении этот термин можно определить как совокупность способов действия учащегося (а также связанных с ними навыков учебной работы), обеспечивающих самостоятельное усвоение новых знаний, формирование умений, включая организацию этого процесса.

Виды универсальных учебных действий:

• личностные
• регулятивные
• познавательные
• коммуникативные

Личностные действия - система ценностных ориентаций младшего школьника, отражающих личностные смыслы, мотивы, отношения к различным сферам окружающего мира. Личностные УУД выражаются формулами “Я и природа”, “Я и другие люди”, “Я и общество”, “Я и познание”, “Я и Я”, что позволяет ребёнку выполнять разные социальные роли (“гражданин”, “школьник”, “ученик”, “собеседник”, “одноклассник”, “пешеход” и др).

Регулятивные действия отражают способность обучающегося строить учебно-познавательную деятельность, учитывая все её компоненты:

• целеполагание
• планирование
• прогнозирование
• контроль
• коррекция
• оценка
• саморегуляция

Познавательные универсальные действия:

• Общеучебные (самостоятельное выделение и формулирование познавательной цели; поиск и выделение необходимой информации; выбор наиболее эффективных способов решения задач в зависимости от конкретных условий; рефлексия способов и условий действия, контроль оценка процесса и результатов деятельности; смысловое чтение как осмысление цели чтения и выбор вида чтения в зависимости от цели; моделирование);
• Логические (анализ объектов с целью выделения признаков, синтез, выбор оснований и критериев для сравнения, классификации объектов, выведение следствий, установление причинно-следственных связей, доказательство, выдвижение гипотез и их обоснование);
• Постановка и решение проблемы (формулирование проблемы, самостоятельное создание способов решения проблем творческого и поискового характера).

Коммуникативные действия:

• планирование учебного сотрудничества с учителем и сверстниками;
• постановка вопросов — инициативное сотрудничество в поиске и сборе информации;
• разрешение конфликтов – выявление, поиск и оценка альтернативных способов разрешения конфликта, принятие решения и его реализация;
• управление поведением партнера — контроль, коррекция, оценка его действий;

Развитие системы универсальных учебных действий в составе личностных, регулятивных, познавательных и коммуникативных действий, определяющих развитие психологических способностей личности, осуществляется в рамках нормативно-возрастного развития личностной и познавательной сфер ребенка.

 

           

 

 

Уважаемые коллеги, посмотрите на слайд и скажите, какое слово объединяет все эти картинки. (СЛАЙД №1)

Мы прекрасно понимаем, что для младшего школьного возраста характерны яркость и непосредственность восприятия, лёгкость вхождения в образы. Дети легко вовлекаются в любую деятельность, особенно игровую.

Игра для них – учёба, игра для них – труд, игра для них – серьёзная форма воспитания.

Настоящее сотрудничество учителя и ученика возможно при условии, что учиться не заставляют, а увлекают.

Задания в занимательной форме позволяют способным ученикам раскрыть и активизировать свои способности. Неуверенным учащимся – развить инициативу, сообразительность, мышление. Даже самые незначительные достижения порождают в ученике веру в свои возможности.

Каждый урок требует чего-то нового, интересного. Важная задача учителя увлечь детей за собой. Поэтому мне близки слова «Игра – это огромное светлое окно, через которое в душу ребенка вливается живительный поток представлений об окружающей действительности». В.А.Сухомлинский (СЛАЙД №2)

Применение игровых технологий позволяет мне добиваться успешных результатов обучения и воспитания младших школьников, которые смогут поставить нужные цели и не боятся сложностей, связанных с их достижением. (СЛАЙД №3)
Требования к подбору игр следующие. (СЛАЙД №4)

1. Игры должны соответствовать определенным учебно-воспитательным задачам, изучаемому материалу.
2. Игры должны строиться с учетом подготовленности учащихся и их психологических особенностей.
3. Игры должны базироваться на определенном дидактическом материале и методике его применения.

Моя задача как учителя – научить каждого ребёнка самостоятельно учиться, сформировать у него потребность активно относиться к учебному процессу. Одно из средств, содержащих реальную возможность осуществления этой задачи – игра, которая способствует развитию умственной деятельности детей. Я использую игры и игровые приёмы на уроках обучения грамоте и чтению, математики, русского языка, окружающего мира. Стоит только мне произнести: «А сейчас мы поиграем» - как ученики мгновенно преображаются: у них появляется интерес, стремление быстро выполнить задание. Сегодня я вам тоже предлагаю поиграть.

  Игра «Видимо – невидимо»

 

- Хочу предложить вашему вниманию игру «Видимо – невидимо».

Играть будем командами, потому надо соблюдать правила: работаем только в своей команде, работаем тихо, потому что каждое неосторожное слово может стать подсказкой для другой команды, что уменьшит ваши шансы на победу.

На доске вывешивается плакат, на котором разными цветами крупным и мелким (но различным издали) шрифтом, «вдоль» и «поперек» написано 15 слов. По истечении 1 мин плакат снимается. А команды записывают все запомнившиеся слова.

Затем команды обмениваются своими записями и сверяют их с плакатом, вывешенным для проверки. Командам желательно вносить исправления в чужие записи ручкой другого цвета.

Проверяющие исправляют ошибки и вписывают «не увиденные» другой командой слова.

Проверенные листочки возвращаются прежней команде для «проверки проверяющих» и выяснения возможных недоразумений, после чего определяются победители. Данные количества записанных слов и ошибок записываются на доске против соответствующего команде цветного квадрата. Выигрывает та команда, в чьих записях оказалось меньше всего ошибок и пропущенных слов.

Социализация.

- Какую учебную задачу преследовала эта игра?

- Какую воспитательную цель выполняла игра?

- Подумайте, на каких уроках и при, изучении каких тем вы можете применять эту игру?

Игровое упражнение «Мозаика».

- Предлагаю вашему вниманию игровое упражнение «Мозаика».

- Вы получили конверты со словами из детских стихов. Стихи разрезаны на слова и фразы. Восстановите эти стихи. Готовые варианты запишите на листочки.

- Зачитайте свои стихи.

Социализация.

- Как вы считаете, это игра или игровое упражнение?

- На каких уроках можно применить это задание?

- Таким образом, можно работать с пословицами. А если это упражнение дополнить и усовершенствовать, то можно применять как игру.

 

Я убедилась, что на таких уроках, где присутствует игра, ученики работают более активно. Особенно радует, что те ученики, которые учатся неохотно, на таких уроках работают с большим увлечением.

А теперь я приведу примеры игр, которые можно использовать на уроках русского языка.

 

Игра «Шифровальщики» (СЛАЙД № 6)

Цель: развитие фонетико-фонематического восприятия процессов анализа и синтеза, обогащение словарного запаса учащихся, развитие логического мышления.

Ход: играют в парах: один в роли шифровальщика, другой – отгадчика.

Шифровальщик задумывает слово и шифрует его.

 

Ж Ы И Л	А Н С К И	К Ь О Н И К
Л Ы Ж И	С А Н К И	К О Н Ь К И

 

Отгадчику предстоит не только отгадать слова, но и выбрать из каждой группы лишнее слово. Например,

А а л т р е к, л а ж о к, р а у к ж к, з о о н к в

(тарелка, ложка, кружка, звонок)

О а р з, с т р а а, ё н к л, р о а м к ш а

(роза, астра, клён, ромашка)

 

В бессмысленный набор букв вставляются слова. Требуется отыскать их как можно быстрее и без ошибок. Найди не меньше 10 названий животных. (СЛАЙД №7)

Задания на концентрацию внимания.

Ребусы (СЛАЙД № 8,9,10)

Ребус это загадка, в которой какое-то слово или фраза зашифрованы комбинацией букв, фигур, знаков. В ребусе скрыта определенная тайна, и ребенок с его стремлением к познанию мира с большим желанием старается разгадать предложенную загадку. При разгадывании ребусов решаются многие задачи: развитие фонематического, слогового анализа и синтеза; закрепление знаний звукобуквенных обозначений; развитие важнейших психических процессов - внимания, памяти, понятийного мышления. Дети учатся видеть, слышать рассуждать. Развивается их способность к переносу полученных интеллектуальных навыков на незнакомый материал.

Игра «Наборщик» (СЛАЙД № 11)

Шарады (СЛАЙД № 12)

СЛАЙД №13

Игровые технологии формируют коммуникативные УУД (умение слышать, слушать, понимать партнера, выполнять согласованно совместные дела, распределять роли, взаимно контролировать действия друг друга, уметь договориться, правильно выражать свои мысли); познавательные УУД (сравнивать, искать хитроумные решения, находить закономерности); личностные УУД (фантазировать, проявлять интерес к окружающему миру, к себе, ориентировать на моральные нормы); регулятивные УУД (планировать, оценивать правильность выполнения действий).

Применение игровых технологий в обучении делает процесс познания наиболее доступным и увлекательным, а усвоение знаний более качественным и прочным.

Игра есть практика развития. Дети играют – потому что развиваются, и развиваются, потому что играют.

Свое выступление я хочу закончить такими словами (СЛАЙД № 14)

Пока идёшь за кем-то вслед,

Дорога не запомнится.

Зато, куда б ты не попал,

И по какой распутице

Дорога та, что сам искал

Вовек не позабудется.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

В воздухе белые хлопья кружатся,
Тихо на землю падает снег,
С каждой снежинкою преображаться
Будет природа и сам человек…

Пришла зима, и выпал снег -
Радость белая для всех.
Раздается детский смех,
Выпал, выпал первый снег!

 

На деревья, на аллеи
Снег летит муки белее,
Легкий-легкий, чистый-чистый,
Мягкий, хрупкий и пушистый.

 

Кто взял санки, кто коньки,
Кто бегом играть в снежки,
Во дворе весёлый смех:
Детям радость – первый снег.

Зимним днем посмотрел я в окошко,
Дворик наш серебром замело, 
Все деревья, дома и дорожки 
Всё вокруг словно вата бело!

Не идется и не едется,
Потому что гололедица.
Но зато отлично падается!
Почему ж никто не радуется?!

Дуют ветры в феврале,
Воют в трубах громко.
Змейкой вьется по земле
Легкая поземка.

Снежок порхает, кружится,
На улице бело.
И превратились лужицы
В прозрачное стекло.

Буря мглою небо кроет,
Вихри снежные крутя;
То, как зверь, она завоет,
То заплачет, как дитя,

За окошком в белом поле –
Сумрак, ветер, снеговей…
Ты сидишь, наверно, в школе,
В светлой комнатке своей.

К.Д.Ушинский писал: “ …чем долее вы будете оберегать ребёнка от серьёзных занятий, тем труднее для него потом переход к ним. Сделать серьёзные занятия для ребёнка занимательными – вот задача первоначального обучения”.

С приходом ребёнка в школу меняется его социальная позиция, ведущая деятельность из игровой превращается в учебную и основным видом деятельности становится учение. Именно игра призвана помочь ребенку пережить период адаптации. Игра формирует устойчивый интерес к учению, снимает напряжение. В процессе игры ребёнок приобретает определённые учебные универсальные действия, обогащает свой внутренний мир, овладевает речью в общении с другими людьми. Поэтому в начальной школе я считаю наиболее приемлемым использование именно игровой технологии.

Я разбила игры на группы по характеру познавательной деятельности.

1.Игры, требующие исполнительской деятельности.

В данных играх дети выполняют действия по образцу или указанию. В процессе таких игр дети знакомятся с простейшими геометрическими фигурами. Их свойствами, овладевают пространственными представлениями. Эти игры часто применяются в первые месяцы обучения в 1-м классе.

2.Игры, в ходе которых дети выполняют воспроизводящую деятельность.

К этой группе относятся игры, которые способствуют формированию вычислительных навыков и навыков правописания.

3.Игры, в которых запрограммирована контролирующая деятельность.

К этому виду можно отнести игры “ Я - учитель”, “ Контролёр”, в которых ребята проверяют выполненную кем-то работу.

4. Игры, с помощью которых дети осуществляют преобразующую деятельность.

В играх данной группы ребята выводят закономерность, которая является ключом к данным заданиям.

Игра “ Придумай слово из данных букв”.

ОСКОЛ - сокол, колос, кол, лоск, сок.

5. Игры, включающие элементы поисковой деятельности.

В процессе игры дети учатся анализировать, находить общее и различие.

Хорошая игра похожа на хорошую работу. В каждой игре есть рабочее усилие и усилие мысли. Игра помогает снять утомление и напряжение, поддерживает внимание. Увлечённые игрой, ученики легче усваивают программный материал, проявляют активность, находчивость, сообразительность, инициативу и смекалку. Хорошая игра похожа на хорошую работу.

Дидактических игр очень много, но при подборе материала к уроку необходимо помнить, что все игры и упражнения должны быть связаны с темой конкретного урока и направлены на достижение конкретной цели.

Одной из основных и, я думаю, самых важных задач в начальной школе является задача научить ребёнка читать. Тот. Кто работал с первоклассниками знает, как нелегко приходится учителю в первые месяцы обучения детей. Как заставить ребёнка слушать, с помощью каких средств и методов сделать обучение увлекательным?

Исходя из игровой задачи, школьники осуществляют игровые действия, которые как бы маскируют сложную мыслительную деятельность, делают ее более интересной. Так, называя предмет, изображенный на картинке, дети вслушиваются в звучание слова, определяют наличие или отсутствие в нем изучаемого звука, затем помещают картинку в домик того или иного цвета.

Сопоставляя букву с изображением знакомых предметов, ребята быстрее запоминают написание заданной буквы. На каждом уроке провожу игры, в ходе которых ребята придумывают слова с изучаемой буквой.

Игра “ Любопытный”

- Как тебя зовут? Андрей

- А фамилия? Азбукин.

Откуда ты приехал? из Астрахани

- А что там растёт? арбузы

- А на чём поедешь обратно? на автобусе

- Какой подарок привезёшь маме? астры

На уроках обучения грамоте и на уроках чтения я провожу артикуляционную разминку, читаем скороговорки и чистоговорки. Эти упражнения развивают подвижность речевого аппарата.

“ Чищу зубы”

Чищу зубы, чищу зубы
И снаружи, и внутри
Не болели чтоб они.

( языком круговые движения)

Надо сказать, что роль учителя остается значительной на всем протяжении игры. Эффективность игры во многом зависит от эмоционального отношения к ней учителя , от его заинтересованности в результатах. Кроме того, поскольку не все школьники одновременно усваивают игровые правила, учитель продолжает помогать им в процессе игры. Эта помощь должна быть по возможности скрытой от других учеников, чтобы у всех – и у слабых, и у сильных – создавалось впечатление равноценности их участия.

Ребенку можно помочь, упростив материал игры, напомнив последовательность выполнения задания или сократив объем мыслительных операций. Например, при изучении темы “Слова, обозначающие предметы” во 2-м классе можно использовать игровое лото, на карточках которого изображены предметы одного назначения, но в разных сочетаниях: кружка, чашка, стакан; чайник, кофейник; миска, тарелка; портфель, ранец, сумка; стул, кресло; люстра, лампа. На карточках для слабых учеников подбор картинок должен быть таков, чтобы они могли узнать каждый из нарисованных предметов, а в случае выигрыша назвать их и записать названия на доске. Упрощение содержания работы помогает слабоуспевающим школьникам не чувствовать себя ущемленными, играть наравне с другими, не терять интереса к игре и даже выигрывать.

Нередко русский язык представляется многим ученикам скучным и неинтересным уроком. Поэтому я задумалась над поблемой повышения интереса к этим урокам.

Например, игру “ Слово - змейка” я провожу, начиная с 1 класса, постепенно усложняя задания. Если в 1 классе ребята составляют слова просто лишь по последней букве предыдущего слова, то в следующих классах я уже знакомую игру делаю более сложной. Можно попросить составить слова с безударными гласными, с парными согласными.

Орфографическая грамотность _ основная часть изучения русского языка. На каждом уроке русского языка я провожу орфографическую разминку.

Горка, горочка, гора,
Под горой есть нора.
В той норе живёт лиса,
Среди всех лесов – краса.
О лисе той не тужите,

Сколько правил здесь, скажите?

Применение на уроках упражнений с элементами какографии способствуют развитию орфографической зоркости. А если ошибки делает какой- нибудь сказочный герой, то исправлять их ещё интереснее.

Я пишу в тетрадь карова,
А карова- нездорова.
Я пишу: сабака фомка,
А сабака лает громко.
Я пишу: бильчоно к тишка,
А бильчонок целит шышкой
Прямо в лоб мне и кричит:
- Лучше правила учи!

Математика- один из наиболее трудных предметов. Включение дидактических игр и упражнений позволяет чаще менять виды деятельности на уроке, что создает условия для эмоционального отношения к содержанию учебного материала, обеспечивает его доступность и осознанность.

“Назови соседей числа”

Эта игра дает возможность каждое число первой сотни рассматривать не изолированно, а в связи с предыдущим и последующим числом.

Средства обучения: мяч или два мяча – большой и маленький (или разного цвета).Содержание игры: учитель бросает мяч то одному, тот другому участнику игры, а те, возвращая мяч, отвечают на вопрос учителя. Бросая мяч, учитель называет какое-либо число, например двадцать один, играющий должен назвать смежные числа –20 и 22 (обязательно сначала меньшее, потом большее).

Возможен и другой, более сложный вариант игры. Возвращая мяч, играющий должен сначала отнять от названного учителем числа единицу, потом прибавить к нему полученную разность. Например, учитель назвал число 11, а играющий должен назвать числа 10 (11-1=10) и 21 (11+10=21).

Эту игру можно провести с двумя мячами: большим и маленьким (или разного цвета). Когда учитель бросает большой мяч, то отвечающий должен, к примеру, прибавить 9 и вернуть мяч обратно, а когда маленький – то отнять 3. Здесь дети не только считают, но и развивают внимание, чтобы не перепутать действия.

Игра “ Старик Хотабыч”.

Однажды в реке нашли старинный сосуд, на котором были начертаны таинственные слова: “ В этот сосуд заключён могущественный джин Гасан Абдурахман ибн Хоттаб за то, что тысячу лет назад он не смог выполнить задание повелителя джинов аль - манфара”.

Задания (на рисунке кувшин с любыми числами)

Найдите “ лишнее” число.

Выпишите чётные, нечётные числа.

Составьте равенства и неравенства.

Увеличьте числа на2.

Уменьшите числа на 2.

Из кувшина вышел вдруг
Добрый джин – наш старый друг.
Кто решит всё без подсказки,
Тех возьмёт с собою в сказку.

Мы готовим ребёнка к жизни. А в жизни не все обязанности занимательны. Если забывать об этом, то занимательность часто превращается в развлекательность. Необходимо помнить об этом, включая игровые упражнения в урок.

Игровые технологии в младшем школьном возрасте

Для младшего школьного возраста характерны яркость и непосредственность восприятия, легкость вхождения в образы. Дети легко вовлекаются в любую деятельность, особенно в игровую, самостоятельно организуются в групповую игру, продолжают игры с предметами, игрушками, появляются неимитационные игры.

В игровой модели учебного процесса создание проблемной ситуации происходит через введение игровой ситуации: проблемная ситуация проживается участниками в ее игровом воплощении, основу деятельности составляет игровое моделирование, часть деятельности учащихся происходит в условно-игровом плане.

Ребята действуют по игровым правилам (так, в случае ролевых игр - по логике разыгрываемой роли, в имитационно-моделирующих играх наряду с ролевой позицией действуют «правила» имитируемой реальности). Игровая обстановка трансформирует и позицию учителя, который балансирует между ролью организатора, помощника и соучастника общего действия.

Итоги игры выступают в двойном плане - как игровой и как учебно-познавательный результат. Дидактическая функция игры реализуется через обсуждение игрового действия, анализ соотношения игровой ситуации как моделирующей, ее соотношения с реальностью. Важнейшая роль в данной модели принадлежит заключительному ретроспективному обсуждению, в котором учащиеся совместно анализируют ход и результаты игры, соотношение игровой (имитационной) модели и реальности, а также ход учебно-игрового взаимодействия. В арсенале педагогики начальной школы содержатся игры, способствующие обогащению и закреплению у детей бытового словаря, связной речи; игры, направленные на развитие числовых представлений, обучение счету, и игры, развивающие память, внимание, наблюдательность, укрепляющие волю.

Результативность дидактических игр зависит, во-первых, от систематическоuj их использования, во-вторых, от целенаправленности программы игр в сочетании с обычными дидактическими упражнениями.

Игровая технология строится как целостное образование, охватывающее определенную часть учебного процесса и объединенное общим содержанием сюжетом, персонажем.
В нее включаются последовательно игры и упражнения формирующие умение выделять основные, характерные признаки предметов сравнивать, сопоставлять их; группы игр на обобщение предметов по определенным признакам; группы игр, в процессе которых у младших школьников развивается умение отличать реальные явления от нереальных; группы игр, воспитывающих умение владеть собой, быстроту реакции на слово, фонематический слух смекалку и др. При этом игровой сюжет развивается параллельно основном содержанию обучения, помогает активизировать учебный процесс, осваивать ряд учебных элементов. Составление игровых технологий из отдельных игр и элементов - забота каждого учителя начальной школы.

В отечественной педагогике имеется ряд таких игровых технологий («Сам Самыч» В.В.Репкина, «Мумми-тролли» томских авторов, персонажи «Волшебника Изумрудного города», «Приключений Буратино» и т.д.), встроенных в основное содержание обучения.

Методика обучения детей теории музыки В.В.Кирюшина. Эта методика основана на соответствии каждому музыкальному понятию одушевленного персонажа (октава - жирафа, терция - сестрица, диссонанс - злой волшебник и т.п.). Все герои испытывают различные приключения, в которых проявляются их сущностные признаки и качества. Вместе с героями дети с трехлетнего возраста незаметно для себя усваивают самые сложные музыкальные понятия и умения, понятия ритма, тональности, начала гармонии.

Игры, требующие от детей исполнительской деятельности.

С помощью этой группы игр дети выполняют действия по образцу или указанию.  В процессе таких игр ученики знакомятся с простейшими понятиями, овладевают счётом, чтением, письмом. В  этой группе  игр можно использовать такие задания: придумать слова, числовые выражения, выложить узор, начертить фигуру подобную данной.

Игры, в ходе которых дети выполняют воспроизводящую деятельность.

К этой группе относятся игры, способствующие формированию вычислительных навыков, навыков правописания. Это «Математическая рыбалка»,  «Кот-буквоед»,  «Лабиринт», «Как добраться до вершины», «Заполни окошечко»,  «Определи курс корабля».

Игры, в которых запрограммирована контролирующая деятельность.

К ним можно отнести: игры «Я учитель», «Контролёр» в которых  ученики выполняют проверку чьей-то работы. Детям раздаются  карточки: на уроках математики с примерами, которые они должны решить. Если ответ совпадёт с номером автобуса, значит, он пассажир; на уроках русского языка карточки со словами - дети должны объяснить орфограмму и вписать букву. Например, автобус с буквой А и слова «малина», «машина», «пальто», «платок».

Игры, требующие от детей преобразующей деятельности.

В этих играх нужно преобразовать слова, числа, задачи  в другие, логически связанные с ними.

 Игры «Числа перебежчики», «Придумай слова из слова», «Собери круговые примеры»

Игры, включающие элементы поисковой деятельности.

Дети должны выявить закономерность, которая является ключом к данному заданию. Ученики очень любят игры данной группы. Им нравится сравнивать, анализировать. Находить общее и различия, интересен поиск недостающего: «Определи   закономерность», «Найди ключ», «По какой тропинке ты пойдешь».

Игровые  ситуации можно разнообразить, изменяя героя, сюжет, правило,  что позволяет использовать дидактические игры на всех уроках в начальной школе. Игры, построенные  на материале различной  степени трудности,  дают возможность осуществлять  дифференцированный подход в обучении детей с разным уровнем   развития.

Игры на базе конструктора ЛЕГО (или любого другого конструктора)

Игра на базе конструктора способствует развитию мелкой моторики, формированию представлений о цвете и форме и ориентировки в пространстве.

 с поделками из конструктора ребенок может играть, ощупывать их, не рискуя испортить, тогда как рисунки, аппликации или фигурки из пластилина не могут быть пригодны для организации игры;

• при использовании конструктора у ребенка получаются красочные и привлекательные поделки вне зависимости от имеющихся у него навыков. Ребенок уже испытывает чувство успеха;
• поскольку конструктор можно расположить не только на столе, но и на полу на ковре, ребенку во время занятия нет необходимости сохранять статичную сидячую позу, что особенно важно для соматически ослабленных детей;
• конструктор безопасен, у ребенка руки остаются чистыми, а убрать поделки можно легко и быстро.

Разными фирмами предлагается широкий выбор наборов: “Дом”, “Аэропорт”, “Зоопарк”, “Семья” и другие. Их можно использовать для развития словарного запаса малыша.

Игры с мелкими предметами

1. “Кто запомнит?”

Оборудование: коробочка с цветными палочками разной величины, образцы, нарисованные на таблицах.Содержание: взрослый показывает ребенку образец 5-10 сек. Ребенок должен внимательно его рассмотреть и запомнить, в каком порядке размещены палочки. Взрослый убирает таблицу, и ребенок самостоятельно выкладывает из палочек рисунок, который он только что видел. По окончанию работы ребенок сверяет рисунок с образцом.

2. “Волшебный куб

Оборудование: “волшебный куб” – их сейчас продается великое множество с различной тематикой (геометрические фигуры, животные, цветы, цифры и т.п.). Можно изготовить самим такой куб: взять коробку в форме куба из плотного картона, подобрать фигурки по выбранной тематике (например, геометрические) примерно одного размера и сделать соответствующие отверстия в коробке. Все можно раскрасить в разные цвета. На первом этапе надо показать ребенку, что каждая фигурка попадает только в одно отверстие, а в другое – нет; затем совместно попытаться разложить фигурки. И только потом можно предоставить ребенку самому попробовать. И если не получиться, попробовать сначала.

Работа с бусами

Отлично развивает руку разнообразное нанизывание. Нанизывать можно все что нанизывается: пуговицы, бусы, рожки и макароны, сушки и т.п. Можно составлять бусы из картонных кружочков, квадратиков, сердечек, листьев деревьев, в том числе сухих, ягод рябины.

Используемые материалы: бусы различной текстуры, леска, нитки, пуговицы, макароны, сушки, шнурки и другие материалы (зависит от фантазии).

Содержание: Взрослый раскладывает на столе бусинки разного размера, но одного цвета (или одного размера, но разных цветов, или разных размеров и разных цветов). Предлагается самостоятельно сделать бусы, в которых чередуются большие и маленькие бусинки, или красные и синие, или круглые и квадратные и т.п. При выполнении этого задания важно, чтобы ребенок не только правильно продевал нитку в отверстия бусинок, но и соблюдал определенную последовательность нанизывания бусинок.

Можно предложить ребенку самому придумать материал для нанизывания и узор.

Рисование

В процессе рисования у детей развиваются не только общие представления, творчество, углубляется эмоциональное отношение к действительности, но формируются элементарные графические умения, столь необходимые для развития ручной ловкости, освоения письма. Рисуя, дети учатся правильно обращаться с графическим материалом и осваивают различную изобразительную технику, у них развивается мелкая мускулатура руки. Рисовать можно черными и цветными карандашами, фломастером, мелом, акварельными красками, гуашью. Безусловно, рисование способствует развитию мелких мышц руки, укрепляет ее. Но надо помнить, что при обучении рисованию и письму специфичны положения руки, карандаша, тетради (листа бумаги), приемов проведения линий.

Оборудование: Краски, карандаши, восковые мелки или пастель, фломастеры и иные материалы. Бумага для рисования должна быть разных форматов и оттенков. Необходимо также иметь кисти разных размеров, губки для закрашивания больших пространств и т.д.

Содержание: Для начала хорошо использовать:

1. обводку плоских фигур. Обводить можно все: дно стакана, перевернутое блюдце, собственную ладонь, плоскую игрушку и т.д. Особенно подходят для этой цели формочки для приготовления кексов;

2. рисование по опорным точкам;

3. дорисовывание второй половины рисунка;

4. рисунок по образцу, не отрывая руки от бумаги.

Хорошо развивает моторную ловкость рисование орнаментов на листах в клетку (графические упражнения) сначала простым карандашом, затем цветными. Выполнять такие упражнения можно с 5 - 6 лет. Дети с интересом занимаются подобным рисованием. Когда рука ребенка немного окрепнет, то рисунки в его исполнении становятся опрятнее и красивее.

Работа с бумагой и ножницами

Изготовление поделок из бумаги также является одним из средств развития мелкой мускулатуры кистей рук. Эта работа увлекает дошкольников, способствует развитию воображения, конструктивного мышления. Работа с бумагой заканчивается определенным результатом, но, чтобы его достичь, нужно овладеть необходимыми навыками, проявить волю, терпение. Важно, чтобы дети испытывали радость от самостоятельно выполненной работы, почувствовали веру в свои силы и возможности. Этому должны способствовать и подобранные в соответствии с возрастом задания, и поощрения взрослых.

Задания по развитию мелкой моторики могут быть включены в такие домашние дела, как:

• перемотка ниток;
• завязывание и развязывание узелков;
• уход за срезанными и живыми цветами;
• чистка металла;
• водные процедуры, переливание воды. Можно предложить помыть посуду, предоставив в распоряжение ребенка пластиковые предметы, или постирать белье (объясните и покажите предварительно все процессы: смачивание, намыливание, перетирание, полоскание, отжимание);
• собирание разрезных картинок;

Общая характеристика работы.

Одной из главных общеобразовательных задач начального обучения математике является формирование вычислительных навыков, которые необходимы как в практической жизни каждого человека, так и в учении.

Цель данной разработки:

·         на конкретном дидактическом материале показать, как можно отрабатывать вычислительные навыки в интересной, увлекательной форме;

·         способствовать привитию детям интереса к математике, общему развитию мышления.

Объектом исследования является учебно-воспитательный процесс.

Предмет разработки - игровые упражнения на уроках и во внеурочное время, обеспечивающие более высокое качество обучения.

В основу разработки положена следующая гипотеза исследования - если методически обоснованно внедрять активную форму обучения, использовать игровые ситуации, различные нестандартные приемы вычисления, то это будет способствовать:

·         обеспечению современного качественного обучения школьников;

·         созданию творческой атмосферы познания, сотрудничества ученика и учителя;

·         повышению активности и самоорганизации учащихся;

• закреплению интереса к изучаемой науке, побуждению к творчеству.
Задачи исследования:

доказать, что дидактическая игра является ценным средством воспитания умственной активности детей, активизирует психические процессы, вызывает у учащихся живой интерес к математике.

Достоверность и обоснованность результатов исследования обеспечиваются:

·         соответствием предлагаемого материала теоретическим положением фундаментальной науки;

·         воспроизводимостью, качественным и количественным анализам;

·         длительностью практического применения, его апробацией с различной по подготовленности аудиторией учащихся.

Научная новизна и теоретическая значимость выполненной работы заключается в следующем:

·         подготовлены различные карточки, перфокарты для проверки усвоения материала;

·         разработаны игры, направленные на активизацию мыслительной
деятельности учащихся, на формирование вычислительных навыков;

• разработан интересный тест для проверки знаний учащихся.
Практическая значимость разработки состоит в:

·         возможности воспроизведения и распространения занимательного
материала, дидактических игр в однотипных школах;

·         внедрение разработанного демонстрационного и раздаточного
материала в практику проведения уроков.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Глава I

Важнейшая задача школы - давать подрастающему поколению глубокие и прочные знания основ наук, вырабатывать навыки, умения, применять их на практике. В связи с этим нужна такая организация обучения, при которой бы дети включались в работу. Многое зависит от учителя: как он организует учебный процесс, и какие формы внеклассной работы предлагает детям. При этом учителю важно учитывать уровень подготовленности детей, их интересы, индивидуальные и возрастные особенности каждого учащегося. Если учитывать все эти моменты, можно так поставить работу, при которой легко добиться высоких результатов.

Математика занимает особое место среди школьных дисциплин. Программой начальной школы по математике поставлена задача повышения качества обучения детей математике. Подчеркнуто, что особого внимания заслуживает формирование вычислительных навыков в табличных случаях, которые должны быть доведены до автоматизма

( как жизненно необходимые ).

Если ученик не усвоил достаточно четко таблицу сложения в 1 классе и таблицу умножения во 2 классе, то это ставит его в весьма трудное положение в 3 классе, так как научиться выполнять письменные действия с многозначными числами можно только в том случае, если хорошо знать таблицу.

В настоящее время, в век компьютерной грамотности значимость навыков устных вычислений ни чуть не уменьшилась. Сейчас при решении практических и производственных задач наблюдается повышенный интерес к вычислительной технике. Наблюдается это и в школе, когда ученики стремятся вычислить значение математического выражения с помощью калькулятора. Если, с одной стороны, считать это положительным явлением, поскольку дети, начиная с начальных классов, приобретают навыки работы с вычислительной техникой, то, с другой стороны, - такое увлечение может тормозить развитие способности ребенка к устным вычислениям, к развитию логического мышления. Решение этой проблемы я вижу не в запретах пользоваться калькуляторами, а в создании атмосферы, где возрастает желание детей производить вычисления устно быстрее, чем на калькуляторе. Например, при умножении числа 7 на 8 ученик не будет прибегать к калькулятору, так как он может сразу назвать результат, зная таблицу умножения.

Прочность и автоматизм навыков достигается в процессе упражнений. Но выполнение однотипных упражнений утомляет детей, поэтому я включаю эти упражнения в игровые ситуации, игры.

Дидактическая игра является ценным средством воспитания умственной активности детей, она активизирует психические процессы, вызывает у учащихся живой интерес к процессу познания. В ней дети охотно приобретают значительные трудности, тренируют свои силы, развивают способности и умения. Она помогает сделать любой учебный материал увлекательным, вызывает у учеников глубокое удовлетворение, создает радостное рабочее настроение, облегчает процесс усвоения знаний. Высоко оценивая значение игры ¹В. А. Сухомлинский писал: "Без игры нет? и не может быть полноценного умственного развития. Игра - это искра, зажигающая "огонек пытливости и любозна­тельности". Глубоко ошибаются те, кто считает, что игра лишь забава и развлечение. Игру можно назвать восьмым чудом света, так как в ней заложены огромные воспитательные и образовательные возможности.

Известный французский ученый Луи де Брайль утверж­дал, что все игры (даже самые простые) имеют много общих элементов с работой ученого. В игре сначала привлекает поставленная задача и трудность, которую можно преодолеть, а затем радость открытия и ощущения преодоленного препятствия. Именно по этому всех людей независимо от возраста привлекает игра.

'Сухомлинский В. А. Изб. пед. соч. - М., 1979 - Т. 1. - с. 103-104.

 

Педагогическая наука предъявляет определенные требования к организации игр, в процессе учения. Перечислю некоторые из них.

1. Игра должна основываться на свободном творчестве
и самодеятельности учащихся. Это не значит, что участники
игры не имеют ни каких обязанностей. Опыт показывает, что
ученики часто относятся к этим обязанностям более
ответственно, чем к учебной или трудовой деятельности.

2. Игра должна вызывать у учащихся только
положительные эмоции, т. е. веселое настроение от удачного
ответа. Поэтому игры должны быть довольно- таки доступны
и привлекательны. Цель игры должна быть достижимой, а ее
оформление - красочным и разнообразным.

3.     В игре обязателен элемент соревнования между
командами или отдельными участниками, что значительно
повышает самоконтроль учащихся, приучает их к четкому
соблюдению установленных правил, а главное хорошо
активизирует деятельность. Не всегда победителями игры
становятся хорошо успевающие учащиеся. Часто много
терпения и настойчивости проявляют в игре те, у кого этих
качеств не хватает для систематического приготовления
уроков.

4.     Игра должна учитывать возрастные особенности
учащегося.

Перед проведением игры надо доступно изложить сюжет, распределить роли, поставить необходимое оборудование, сделать нужные записи на доске.

Приведу некоторые игры и занимательные упражнения, которые использую в работе с классом почти на каждом уроке, начиная с первого года обучения. Проводятся они в начале или конце урока в зависимости от цели и задачиданного занятия. На игру я отвожу от 5 до 10 минут. Ценность дидактической игры я определяю не по тому, какую реакцию она вызывает со стороны детей, а учитываю, на сколько она помогает решать учебную задачу применительно к каждому ученику. Выбирая какую-либо дидактическую игру для урока, тщательно продумываю следующие вопросы:

1. Цель игры. Какие умения и навыки будут
формироваться в процессе ее проведения?

2.     Какие воспитательные цели преследуются в процессе
игры?

3.     Посильна ли она для учащихся моего класса?

4. Все ли учащиеся будут в одинаковой степени
участвовать в игре?

5. Подведение итогов игры.

Глава II

Одна из важнейших задач обучения в первом классе - обеспечить твердое усвоение таблицы сложения в пределах 20 и соответствующих случаев вычитания. С первых уроков при изучении раздела "Нумерация чисел первого десятка», использую прежде всего такие игры, с помощью которых дети осознают приемы образования каждого последующего и предыдущего чисел. На этом этапе предлагаю ученикам игру "Составим поезд".

Содержание игры. Учитель вызывает к доске поочередно учеников. Каждый из них, выполняя роль вагона, называет свой номер. Например, первый вызванный ученик говорит: "Я - первый вагон". Второй ученик, выполняя роль второго вагона, цепляется к первому вагону (кладет левую руку на плече ученика, стоящего впереди) называет свой порядковый номер, остальные составляют пример: "Один да один, получится два". Затем цепляется третий вагон, и все дети по сигналу- учителя составляют пример на сложение: "Два да один - это три". И так далее. Потом вагоны (ученики) отцепляются по одному, а класс составляет примеры вида: "Три без одного - два. Два без одного - один". И т. д.

Учащиеся в игре закрепляют знания о порядковом и количественном значении числа и снова делают обобщение, как образуется предыдущее и последующее число. При изучении нумерации в пределах 10 необходимо довести до понимания детей, что последнее названное число обозначает общее количество всей группы предметов. С этой целью я провожу игру "Хлопки". На магнитном моделеграфе размещаю по секторам от 1 до 10 рисунков. Открывая по очереди сектор за сектором, предлагаю сосчитать число рисунков и по моему сигналу похлопать столько же раз, сколько открыто рисунков, и показать нужную цифру.

Практика показывает, что положительную роль в формировании навыков сложения и вычитания в пределах 10 играет установка на запоминание каждого числа. Поэтому уже в теме "Числа от 1 до 10" наряду с усвоением принципа образования натурального ряда чисел уделяю внимание рассмотрению всех случаев состава чисел. В основе усвоения состава числа лежит практическая деятельность с предметными множествами. С этой целью использую кружки, квадраты и другие фигуры, закрашенные в разные цвета с одной и с другой стороны. Так ученикам предлагаю положить три синих кружочка, затем перевернуть один из них. Полученная картинка дает наглядное представление о том, что число три можно получить, объединив 2 синих кружка и 1 красный.

 

 

 

2 +1 = 3

 

 

 

 

 

 

Забей мяч в ворота

Дидактическая цель игры. Закрепить знания о составе числа.

Описание игры. На доске (плакате) нарисованы футбольные ворота, а на сетке написано

число. Задание – составить за

определённое время как

можно больше примеров с ответом 7.

Можно дать задание каждому ряду, но с разными числами.

Появляется запись: 1 + 6 = 7

2 + 5 = 7

3 + 4 = 7

«Игру в слова» провожу так: на доске написаны слова. Зачёркивается несколько букв. Дети читают слово, получившееся из остальных букв и записывают примеры.

М

А

Г

Н

И

Т

О

Ф

О

Н

10 – 4 = 6 4 + 6 = 10

Для совершенствования вычислительных навыков включаю в урок игру "Дополни до...". На доске прикреп­ляется карточка с числом 6. Показываю по очереди карточки с числами 2 (3, 5, 1, 4), учащиеся дополняют каждое число до 6, показывая соответствующие карточки 4 (3, 1, 5, 2).

Часто на уроках я использую сказочных героев. Дети очень любят игру "Помоги Незнайке", "Помоги Буратино". На доске прикрепляется портрет сказочного героя и изображаются схемы:

 

 

 

 

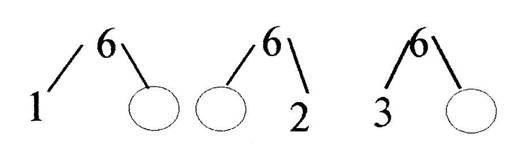
Дети с удовольствием заполняют пустые клеточки (кружочки) и составляют таблицу:

 

6

1

2

3

4

5

5

4

3

2

1

Главная трудность сложения и вычитания чисел с переходом через десяток состоит в представлении второго числа в виде суммы двух слагаемых, одно из которых дополняет первое слагаемое до 10. Например, при сложении 7 и 5 второе слагаемое 5 необходимо представить в виде суммы чисел 3 и 2 и прибавить к 7 сначала 3, а потом 2.

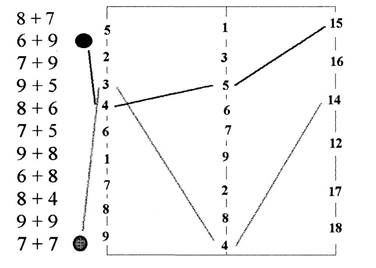Для закрепления изученного приема использую игру "Забей гол в числовые ворота". Дидактическая цель. Закреплять приемы сложения и вычитания в пределах 20. Оборудование. Рисунок числовых ворот на доске. Содержание. До урока на доске рисую мячи и числовые ворота. Левее рисунков мячей записываю примеры. Сообщаю детям правила игры. Направление удара мяча зашифровано примером. Способ решения каждого примера можно отыскать на числовых воротах. Ученики должны правильно загнать мяч в числовые ворота, показать путь его движения, соединить линией пример с той парой числовых ворот, на которых записан прием решения примера, а затем гнать мяч к третьим числовым воротам, где записан ответ примера.

 

 

 

 

 

 

 

 

 

Ученики выходят поочередно к доске и загоняют мяч в числовые ворота, соединяют пример с парой чисел, в которых представлен состав второго слагаемого, одно из которых дополняет первое слагаемое до 10.

Центральной задачей второго года обучения является изучение таблицы умножения и деления. Ученики должны твердо знать таблицу умножения и приобрести необходимую беглость вычислений при решении соответствующих примеров на деление - этого требует программа.

Современная методика требует, чтобы дети не только знали таблицу, но и поняли принцип ее составления, дающий возможность находить любое произведение. Ученик должен не только выучить и запомнить результаты табличного умножения, но и уметь при необходимости вычислить результат самым кратчайшим путем.

Несмотря на то, что все случаи умножения изучаются по единому алгоритму, уроки проходят живо и увлекательно, с неослабевающим вниманием учащихся и даже творческим азартом. То, что детям известен план работы над столбиком таблицы, является прекрасным стимулом в процессе обучения. К примеру, работу по составлению таблиц умножения и деления с числом 9, можно провести так же, как с другими числами, повторяя ранее рассмотренные случаи умножения и деления с числом 9, а можно познакомить учащихся с некоторыми секретами, которые дают возможность увидеть табличные случаи умножения в другом ракурсе. 9 ∙ 2 означает, что число 9 надо взять слагаемым 2 раза 9 + 9; но вместо двух раз по девять, предлагаю взять два раза по десять (учащимся показываю два пучка палочек), тогда в каждом из них окажется по одной лишней палочке, что означает 9 ∙ 2 есть два десятка без двух единиц (18).

Аналогично иллюстрируется, что 9 ∙ 3 есть три десятка без трех единиц. При дальнейшем составлении таблицы обращаю внимание детей на то, что второй множитель показывает число десятков и количество единиц, которые необходимо вычесть:

 

9-2=18 (два десятка без двух единиц)

9 • 3 = 27 (3 десятка без 3 единиц)

9 • 4 = 36 (4 десятка без 4 единиц)

9 • 5 = 45 (5 десятков без 5 единиц) и т. д.

9 • 6 = 54

9 • 7 = 63

9 • 8 = 72

9-9 = 81

После составления таблицы предлагаю детям вни­мательно посмотреть и отыскать другие секреты. Как пра­вило, ребята находят их. Они замечают; что десятки в ответах образуют отрезок натурального ряда чисел: 1, 2, 3, 4,...8, а единицы при этом убывают: 8, 7, 6, 5, ... 1; что сумма цифр каждого произведения равна 9; что при умножении 9 на четное число, получается четное произведение, а при умножении на нечетное - нечетное.

2-9=18 (1 + 8 = 9)

3 • 9 = 27 (2 + 7 = 9)

4-9 = 36 (3 + 6 = 9)ит.д.

 

При таком подходе к составлению таблицы ученики являются не просто пассивными созерцателями, а становятся активными участниками учебного процесса, проявляют смекалку, изобретательность, упорство. Такие исследования, пусть еще очень маленькие, могут стать дорогой к открытию. Приведу некоторые игры, помогающие учащимся просто усваивать таблицу умножения и деления.

Поймай рыбку.

На доске висит таблица, на которой изображен аквариум с

рыбками, на каждой рыбке записан пример:

54 ׃ 9

7 ∙ 9

48 ׃ 6

72 ׃ 8

36 ׃ 9

7∙6

8∙7

56 ׃ 8

4∙8

3∙4

Двое учеников выходят к доске и по команде начинают решать примеры. Остальные учащиеся выполняют задание в тетрадях. По истечении времени, отведенного на вычисления, учащиеся сверяют свои ответы с доской. Тот из учеников у доски, кто решил примеров больше и не допустил ошибок, тот и поймал больше рыбок. Он и считается лучшим рыбаком. Не подведи друга!

К доске выходят одновременно двое (четверо) учеников. Учитель читает пример, например 6∙7. Предлагаю составить четыре примера на умножение и деление. Если примеры составлены и решены верно, одобряю ребят за слаженность в работе. Запись на доске выглядит так: 6 ∙ 7 =42 7 ∙ 6 = 42

42 ׃ 7 = 6 42 ׃ 6 = 7. Здесь очень важно, чтобы дети усвоили способ нахождения частного по известному произведению, понимали, что из примера

7 ∙ 6 = 42 вытекает 42 ׃ 7 = 6, 42 ׃ 6 = 7.

Помоги Незнайке!

На доске вывешивается картинка с изображением Незнайки и карточек с примерами.

7 ∙ 5

 

8 ∙ 6

 

9 ∙ 9

 

4 ∙ 5

 

6 ∙ 3

 

8 ∙ 4

А

К

С

К

А

З

 

Даётся задание: «Помогите Незнайке разложить карточки в порядке уменьшения результатов действий». Выполнив задание, дети читают слова –сказка.

Игра «Не скажу»

Эта игра способствует целенаправленному формированию механизмов переключения внимания. Игра строится так: учащиеся по очереди называют числа от 1 до 40. вместо чисел, которые делятся, например на 2, они говорят: «Не скажу!»

Здесь механизм переключения внимания состоит в том, что обычно произносимое учащимися при проверке табличного умножения заменяется выражением «Не скажу» в процессе называния натурального ряда чисел. Эту игру можно проводить и на перемене.

Игра на внимание.

Учитель бросает мяч ученику и называет пример, ученик говорит ответ и возвращает мяч учителю. Игру можно проводить в качестве физминутки и на перемене.

Кроме этих игр, можно проводить игры «Кто больше соберёт грибов», «Садовники», «Делится не делится», «День и ночь» и другие

Использование таких игр помогает воспитывать интерес к изучению табличных случаев умножения и деления, активизирует внимание учащихся и способствует более прочному усвоению материала.

При проведении устного счёта я часто включаю упражнения и задачи, составленные в рифмованной форме. Это оживляет работу в классе, вносит элемент занимательности.

Эти упражнения я использую при подготовке к изучению умножения, при закреплении таблиц умножения, для иллюстрации решения задач на умножение, для иллюстрации связи сложения и умножения.

Весёлые задачи.

 

Сколько нужно пар сапог,

Чтоб обулся осьминог? (8:2 = 4)

* * *

Поручил учитель Коле

Сосчитать лопаты в школе.

Он лопаты сосчитал

И об этом так сказал:

- В трех углах по пять лопат,

У стены семь штук лежат,

Всех же 23 лопаты.

Вы согласны с ним, ребята? (5 ∙ 3 + 7 = 22)

* * *

Девять расписных матрешек, В каждой пять дочурок-крошек. Если бы все дочки рядом встали,

Сколько бы вы их насчитали? (5 ∙ 9 = 45)

* * *

Гуляли по аллейке

Куриные семейки.

У каждой мамы-квочки

Три сына и две дочки.

Сколько всех цыплят,

Мы спросим.

Если квочек - восемь? ((3 + 2) ∙ 8 = 40)

К третьему-четвёртому классу учеников все больше интересует результат игры, появляется чувство коллективизма, взаимопомощи, их мало устраивает личная победа, возникает желание оказать посильную помощь соседу по парте, команде. В это время учеников все больше привлекают игры-соревнования: "Чей ряд лучше?", "Кто скорее, кто быстрее?", "Набери тысячу" и т. д.

При изучении многозначных чисел провожу игру "Многозначные числа". Перед классом выстраиваются 9 человек группами по 3. У каждого в руках блокнот-табло с цифрами от 0 до 9. Учитель читает многозначное число, а ученики слева направо открывают такие цифры, на месте, какого разряда каждый из них стоит.

После двух-трех заданий ученики меняются местами, затем команда производит замену допустивших ошибки игроков. Выигрывает та команда, представители которой сделали меньше ошибок или вообще не сделали.

 

Среди общеучебных навыков и умений, которыми должны овладеть учащиеся в процессе обучения, особое место занимают умения контролировать и оценивать свою деятельность. Эти умения успешно формируются при использовании личностно-ролевой формы организации учебного процесса как частного вида дидактической игры. С этой целью провожу игру "Учитель - ученик". В течении урока одни дети выполняют роль учителя, другие - оценщика, третьи - контролера. Ученики пробуют свои силы: необходимо так провести урок, чтобы было интересно и чтобы тебя слушали. При этом все многообразие деятельности учителя распределяется между самими учениками. Еще пример: для проверки знаний таблицы умножения на уроках трудового обучения каждый ученик делает карточки с отверстиями, на которых с одной стороны записана таблица, а с другой стороны ответы. Ребенок, выполняющий роль учителя, берет в руки карточку и вставляет в отверстие карандашик, ребенок, выполняющий роль ученика, читает пример рядом с отверстием и говорит ответ. Затем дети меняются ролями. Подобные игры могут реализовываться в парной или групповой работе.

Любят дети игры, в основе которых лежат так называемые «магические квадраты». При знакомстве с магическим квадратом детям предлагаю сложить числа по строкам, по столбикам, по диагоналям.

 

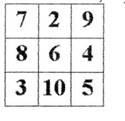
Выполнив задание, ученик убеждается в том, что все суммы равны.

Далее задания усложняются.

1. Заполнение пропусков в предложенном квадрате.

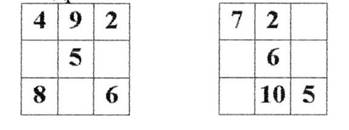
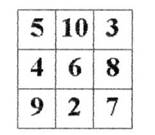2.Преобразование занимательных квадратов. Например, дан магический квадрат: 

 

 

 

 

Составить подобный квадрат, увеличивая или уменьшая каждое число на несколько единиц.

Увеличивая на 4 Уменьшая на 2

получим квадрат: получим квадрат:

 

 

 

 

 

 

 

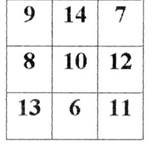
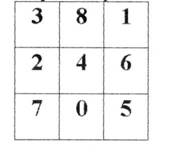
Наблюдения за работой на уроке показывает, что дети с удовольствием выполняют подобного рода задания. С магическими квадратами можно организовать фронтальную, индивидуальную и групповую работу.

Хочу поделиться двумя способами составления занимательных квадратов.

I способ

Для составления занимательных квадратов подбираются 9 чисел, разность между соседними числами должна быть равна постоянному числу. Например: 1, 3, 5, 7, 9, 11, 13, 15, 17. в этом ряду подчёркиваем вторую тройку чисел. Сложив эти числа, получаем сумму занимательного квадрата (7 + 9 + 11 =27). Эту тройку чисел располагаем по любой диагонали. Рядом с самым большим числом (11) располагаем самое маленькое число в ряду (1), либо самое большое число ряда (17) с самым маленьким из подчёркнутых – 7. получаем квадраты:

 

7

17

 

 

 

1

11

 

9

 

 

9

 

 

 

11

 

7

 

 

Учащиеся производят действия, заполняют все клетки в квадратах. Данные квадраты можно заменить другими, увеличив каждое число на несколько единиц или в несколько раз.

II способ

Чтобы составить занимательный квадрат, надо взять число, которое делится на 3. например сумма равна 30. При составлении занимательного квадрата учителю достаточно воспользоваться следующим правилом: S, m, k – целые числа, причём m + k < S ׃ 3. Например: S =30, тогда S ׃ 3 =10. Для m и k можно взять числа 4 и 3, так как 4 + 3 < 10. Находим, что S ׃ 3 + m = 10 + 4 =14, S ׃ 3 – m = 10 – 4 = 6, S ׃ 3 + k = 10 +3 = 13, S ׃ 3 – k = 10 – 3 =7, после чего по формуле заполняем клетки. ( Этот способ составления занимательного квадрата предлагается для учителя)

 

S/3+m

 

S/3+k

 

14

 

13

 

S/3

 

 

10

 

S/3-k

 

S/3-m

 

7

 

6

Большое значение для выработки прочих вычислительных навыков имеет не только количество выполненных упражнений, но и их темп выполнения. С этой целью провожу игру "Лучший счетчик". Раздаю детям карточки, покрытые пленкой, фиксирую время.

Приведу образцы примерных карточек:

I класс III класс

 

2 + 1 =

1 + 3 =

4 + 2 =

5 – 2 =

4 – 3 =

6 + 2 =

5 + 3 =

6 – 5 =

3 + 3 =

5 – 3 =

4 – 2 =

4 + 1 =

7 – 3 =

8 – 6 =

18 ∙ 5 =

23 ∙ 4 =

16 ∙ 6 =

33 ∙ 3 =

47 ∙ 2 =

24 ∙ 4 =

12 ∙ 6 =

24 ׃ 4 =

30 ׃ 6 =

54 ׃ 6 =

42 ׃ 7 =

9 ׃ 3 =

56 ׃ 7 =

12 ׃ 3 =

 

Предлагая учащимся подобные карточки, определяю время для самостоятельной работы, например: 10 минут. Каждый ученик записывает только ответ фломастером.

Наблюдения показывают, что систематическое выполне­ние упражнений в ограниченные сроки оказывает заметное влияние на темп работы ученика, заставляет его быть сосредо­точенным, а отсюда и уровень сформированности навыка постепенно повышается.

Для учета уровня сформированности навыков табличных действий веду специальную тетрадь, в которой фиксирую результаты не только устного опроса по таблицам, но и письменных проверочных работ.

Для этого использую таблицу:

 

Ф.и. ученика

№ карточки

Кол-во решённых примеров

Из них верно

Ошибки

Алиев Р

1

14

12

2

Бирюков Д.

2

15

1

2

Пискаева Д

3

16

16

0

 

На внеклассных занятиях по математике я знакомлю своих четвероклассников с необычными приёмами вычисления. Ученики с интересом используют их при решении, как примеров, так и задач. Приведу примеры устных вычислений.

1. Умножение двузначного числа на 11.

32 ∙ 11 = 352

Приём: между цифрами первого множителя вписываем сумму этих цифр.

Между цифрами 3 и 2 вписываем сумму этих цифр 3 + 2= 5

1.     Умножение трёхзначного числа на 101.

125 ∙ 101 = 12625

Приём: увеличиваем первый множитель на число его сотен и приписываем к нему справа две последние цифры первого множителя.

1. 125 + 1 =126

2. 12625

 

Опыт использования игрового материала на уроках математики и во внеклассной работе показывает, что в первую очередь предложенные выше задания вызывают интерес у учащихся, дети с удовольствием принимаются их выполнять, что делает процесс формирования вычислительных навыков внутренне мотивированным. Кроме того, использование математических игр способствуют развитию мышления, умения планировать и контролировать свою деятельность.

В основе любого творчества лежит знание, поэтому в процессе подготовки к каждому новому учебному году я стараюсь познакомиться с новейшими методическими пособиями, перечитываю статьи в журнале "Начальная школа" и беру на вооружение все то, что можно использовать при работе с данным контингентом учащихся.