Кировский район

Муниципальное бюджетное общеобразовательное учреждение города                                                                  Новосибирска «Средняя общеобразовательная школа № 182 с углубленным изучением литературы и математики имени 46-го гвардейского Таманского Краснознаменного ордена Суворова III  степени женского авиационного полка легких ночных бомбардировщиков»

 

 

 

 Секция МАТЕМАТИКА

                                         Тема: Симметрия в живой природе

                                         Лапина Ульяна,9А класс

 

 

 

 

 

 

                                                                                                           Учитель-консультант:

                                                                                              Качесова Олеся Михайловна,

                                                                                               учитель математики высшей

                                                                                            квалификационной категории,

                                                                                           контактный телефон 342-92-98

 

 

 

 

                                                  

 

                                                    Новосибирск - 2021

 

 

                                       Содержание

 

Введение…………………………………………………………………….................3

1.     Цели проектной работы, задачи, актуальность, объект, предмет, гипотеза исследования, вопросы…………………………………………………………4

 

ГЛАВА I. Что такое «симметрия»?

1. Что такое симметрия? Виды симметрии............................................................5

2. Роль симметрии в нашей жизни…………………………………………….….8

2.1. Центральная симметрия...............................................................................9

          2.2. Осевая симметрия.........................................................................................10

          2.3. Зеркальная симметрия ………………….………........................................11

          2.4. Поворотная симметрия.................................................................................13

 

ГЛАВА II.  Симметрия в природе.

1. Значение симметрии в познании природы………………..................……............14

2. Симметрия в живой природе. Асимметрия и симметрия.   …..............................17

3.Симметрия растений………………………..............................................................19

4. Симметрия животных……………………………....................................................21

5. Человек ― существо симметричное…………………............................................24

Результаты опроса........................................................................................................26

Заключение……………………………………………………….…..…....................27

Список литературы……………..........……………………………….......................28

 

 

 

 

 

 

 

 

 

 

                                                        ВВЕДЕНИЕ

Симметрия "...быть прекрасным - значит быть симметричным и соразмерным."

 Платон (древнегреческий философ, 428 – 348 г. до н.э.)

Среди бесконечного разнообразия форм живой и неживой природы в изобилии встречаются такие совершенные образцы, чей вид неизменно привлекает наш взгляд и ласкает наше внимание. Мы постоянно любуемся прелестью каждого отдельного цветка, мотылька или раковины и всегда пытаемся проникнуть в тайну их красоты. Внимательное наблюдение обнаруживает, что основу красоты многих форм, созданных природой, составляет симметрия, точнее, все её виды ― от простейших до самых сложных.

Мы выбрали для исследования очень необычную тему: «Симметрия в природе», потому, что она связана с интересующим нас вопросом о гармонии нашего мира.

 Понятие симметрии проходит через всю многовековую историю человеческого творчества. Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. В своём проекте я покажу, что законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь подчиняются принципам симметрии. Мы узнаем, что существует множество видов симметрии, как в растительном, так и в животном мире, но при всём многообразии живых организмов, принцип симметрии действует всегда, и этот факт ещё раз подчёркивает гармоничность нашего мира. В нашей исследовательской работе будет отмечено так же, что помимо симметрии существует понятие и асимметрии. Симметрия лежит в основе вещей и явлений, выражая нечто общее, свойственное разным объектам, тогда как асимметрия связана с индивидуальным воплощением этого общего в конкретном объекте.

 Асимметрию можно рассматривать как разграничительную линию между живой и неживой природой. Для неживой материи характерно преобладание материи, при переходе от неживой к живой материи на микроуровне преобладает асимметрия.

Было интересно, потому что данная тема затрагивает не только математику, хотя она и лежит в её основе, но и другие областные науки, техники, природы. Симметрия, как мне кажется, является фундаментом природы, представление о котором слагалось в течение десятков, сотен, тысяч поколений людей.  Я обратила внимание на то, что во многих вещах, в основе красоты многих форм, созданных природой, составляет симметрия, точнее, все её виды ― от простейших до самых сложных. Можно говорить о симметрии, как о гармонии пропорций, как о «соразмерности», регулярности и упорядоченности.

Нам это важно, потому что для многих людей математика ― скучная и сложная наука, но для меня математика ― не только цифры, уравнения и решения, но и красота в строении геометрических тел, живых организмов и даже является фундаментом для многих наук.

 

 

 

 

 

 

Цели проектной работы:

·                    Раскрыть особенности симметрии видов в природе.

·                    Показать всю привлекательность математики, как науки её взаимосвязь с природой в целом.

·                    Узнать, присутствует ли симметрия в окружающем нас мире.

·                    Изучить особенности различных видов симметрии в природе.

Для достижения поставленной цели, был определен ряд задач:

·        Проанализировать литературу по исследуемой проблеме;

·        Изучить основные виды симметрии;

·        Подбор материала по теме «Симметрия в природе», и его обработка.

·        Систематизация и обобщение собранного материала.

·        Провести опрос среди учащихся 9 класса.

·        На результатах опроса сделать заключение.

Актуальность: Симметрия окружает человека, находя своё проявление как в живой, так и не в живой природе. Объяснение законов симметрии важно для понимания красоты, жизни.

Объектом исследования: Понятие «симметрия».

Предмет исследования: Особенности различных видов симметрии в природе.

Гипотеза исследования: Показать важную, исключительную роль принципа симметрии в научном познании мира.

Вопросы:

1.     Как часто вы встречали симметрию в живой природе?

1)Часто.

2) Редко, но бывает.

3) Очень редко.

4)Не обращали внимание.

 

2.     Сколько видов симметрии вы знаете?

3.     Приведите пример зеркальной симметрии.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                                     

                                                           ГЛАВА I

Что такое «симметрия»?

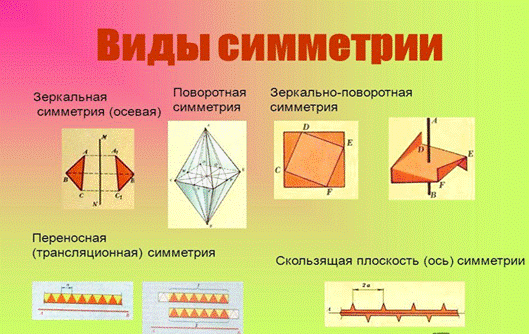
1.Что такое симметрия. Виды симметрии.

Существует множество понятий о симметрии.

Симметрия – это соответствие, неизменность (инвариантность), проявляемых при каких-либо изменениях, преобразованиях (например: положения, энергии, информации, другого). Так, например, сферическая симметрия тела означает, что вид тела не изменится, если его вращать в пространстве на произвольные углы (сохраняя одну точку на месте). Двусторонняя симметрия означает, что правая и левая сторона относительно какой-либо плоскости выглядят одинаково.

Симметрия. Основное понятие.

Симметрия – это определённый геометрический порядок в расположении сходственных частей тела, имеет непосредственное отношение к характеру. Симметрия является жизненно важным признаком, который отражает особенности строения, образа жизни и поведения животного.

Симметрия – это соразмерность, одинаковость в расположении частей чего-либо по противоположным сторонам от точки, прямой или плоскости, прямой или плоскости.

Симметрия («соразмерность») – это закономерное расположение подобных (одинаковых) частей тела или форм живого организма, совокупности живых организмов относительно центра или оси симметрии.

При этом подразумевается, что соразмерность – часть гармонии, правильного сочетания частей целого. В физике общепринято выделять две формы симметрии: геометрическую и динамическую. Симметрии, выражающие свойства пространства и времени, относят к геометрической форме симметрии. Примерами геометрических симметрии являются: однородное пространство и время, изотропность пространства, пространственная четность, эквивалентность инерциальных систем отсчета. Симметрии, непосредственно не связанные со свойствами пространства и времени, выражающие свойства определенных физических взаимодействий, относят к динамической форме симметрии. К динамическим симметриям относят симметрии внутренних свойств объектов и процессов, например симметрии электрического заряда. Геометрические и динамические симметрии можно рассматривать еще в одном аспекте, как внешние и внутренние симметрии.

Отсутствие или нарушение симметрии называют асимметрией или аритмией.

К основным формам геометрической симметрии относятся:

·       зеркальная симметрия;

·       осевая симметрия;

·       центральная симметрия;

·       вращательная симметрия;

·       скользящая симметрия;

·       точечная симметрия;

·       поступательная симметрия;

·       винтовая симметрия;

·       неизометричная симметрия;

·       фрактальные симметрии.

Кроме этого существует:

·       радиальная симметрия;

·       прирадиальная симметрия;

·       билатеральная симметрия.

В курсе планиметрии мы познакомились с движениями плоскости, т. е. отображениями плоскости на себя, сохраняющими расстояния между точками. Введем теперь понятие движения пространства. Предварительно разъясним, что понимается под словами отображение пространства на себя. Допустим, что каждой точке М пространства поставлена в соответствие некоторая точка М1 причем любая точка М1 пространства оказалась поставленной в соответствие какой-то точке М. Тогда говорят, что задано отображение пространства на себя. Говорят также, что при данном отображении точка М переходит (отображается) в точку М1. Под движением пространства понимается отображение пространства на себя, при котором любые две точки А и В переходят (отображаются) в какие-то точки А1 и В1 так, что А1В1=АВ. Иными словами, движение пространства — это отображение пространства на себя, сохраняющее расстояния между точками. Примером движения может служить центральная симметрия — отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М, относительно данного центра О.

Осевой симметрией с осью а называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М1 относительно оси а.

Зеркальной симметрией (симметрией относительно плоскости) называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей относительно плоскости точку М1.

Поворотная симметрия предполагает наличие некоторого центра, относительно которого происходит многократный поворот одного итого же структурного фрагмента. (слайд 6)

Трансляционной симметрией называется многократное повторение одного и того же фрагмента структуры в пространстве или во времени. Примером трансляционной симметрии может служить любой орнамент.(слайд 7)

Однако наряду с привычными формами симметрии существуют и другие виды симметрии:

Винтовая симметрия – это симметрия объекта относительно группы преобразований, являющихся композицией преобразования поворота объекта вокруг оси и переноса его вдоль этой оси.( слайд 8)

Поворотная симметрия предполагает наличие некоторого центра, относительно которого происходит многократный поворот одного итого же структурного фрагмента.( слайд 9)

 

 

 

2.Роль симметрии в нашей жизни

Симметрия является фундаментальным свойством природы, представление о котором, как отмечал академик Вернадский, «слагалось в течение десятков, сотен, тысяч поколений». «Изучение археологических памятников показывает, что человечество на заре своей культуры уже имело представление о симметрии и осуществляло её в рисунке и в предметах быта. Надо полагать, что применение симметрии в первобытном производстве определялось не только эстетическими мотивами. Но в известной мере и уверенностью человека в большей пригодности для практики правильных форм». Это слова другого нашего замечательного соотечественника, посвятившего изучению симметрии всю свою жизнь, академика А. В. Шубникова (1887 — 1970 гг.)

Первоначальное понятие о геометрической симметрии как о гармонии пропорций, как о «соразмерности», что и означает в переводе с греческого слова «симметрия», с течением времени приобрело универсальный характер и было осознано как всеобщая идея неизменности относительно некоторых преобразований.

Симметрия воспринимается в нашей жизни и вообще человеком как проявление закономерности, порядка, царящего в природе. Восприятие же закономерного всегда доставляет нам удовольствие, сообщает некоторую уверенность и даже бодрость.

В нашей жизни мы повседневно, всегда и везде встречаемся с симметрией. Это симметричные предметы и геометрические фигуры, живая природа и зеркальная симметрия и т.д. Итак, «сфера влияния» симметрии поистине безгранична. Природа — наука — искусство. Всюду мы видим противоборство, а часто и единство двух великих начал — симметрии и асимметрии, которые во многом определяют гармонию природы, мудрость науки и красоту искусства. Мы видели, что симметрия форм живой природы обязана своим существованием, прежде всего закону тяготения. Но тяготение — вечный закон природы; значит, вечна и симметрия и она всегда будет ассоциироваться с красотой.

Симметрия воспринимается нами, как покой, скованность, закономерность, тогда как асимметрия означает движение, свободу, случайность.

Теперь мы, понаблюдав и изучив специальную литературу, посмотрим, где найдет свое отображение симметрия. Почему симметрия буквально пронизывает весь окружающий нас мир?

2.1. Центральная симметрия

Введём понятие центральной симметрии: «Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры». Поэтому говорят, что фигура обладает центральной симметрией.

Понятия центра симметрии в «Началах» Евклида нет, но, однако в 38-ом предложении 6 книги содержится понятие пространственной оси симметрии. Впервые понятие центра симметрии встречается в шестнадцатом веке. В одной из теорем Клавиуса, гласящей: «Если параллелепипед рассекается плоскостью, проходящей через центр, то он разбивается пополам и, наоборот, если параллелепипед рассекается пополам, то плоскость проходит через центр». Лежандр, который впервые ввёл в элементарную геометрию элементы учения о симметрии, показывает, что у прямого параллелепипеда имеются 3 плоскости симметрии, перпендикулярные к рёбрам, а у куба 9 плоскостей симметрии, из которых 3 перпендикулярны к рёбрам, а другие 6 проходят через диагонали граней.

Примерами фигур, обладающих центральной симметрией, являются окружность и параллелограмм. Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма ― точка пересечения его диагоналей. Любая прямая также обладает центральной симметрией. Однако, в отличии от окружности и параллелограмма, которые имеют только один центр симметрии, у прямой их бесконечно много ― любая точка прямой является центром её симметрии. Примером фигуры, не имеющей цента симметрии, является произвольный треугольник.

В алгебре при изучении чётных и нечётных функций рассматриваются их графики. График чётной функции при построении симметричен относительно оси координат, а график нечётной функции ― относительно начала координат, т.е. точки О. Значит, нечётная функция обладает центральной симметрией, а чётная функция ― осевой.

Таким образом, две центрально симметричные плоские фигуры всегда можно наложить друг на друга, не выводя их из общей плоскости. Для этого достаточно одну из них повернуть на угол 180 около центра симметрии. Как в случае зеркальной, так и в случае центральной симметрии плоская фигура непременно имеет ось симметрии второго порядка, но в первом случае эта ось лежит в плоскости фигуры, а во втором ― перпендикулярна к этой плоскости. (слайд 12)

2.2. Осевая симметрия

Понятие осевой симметрии предоставлено следующим образом: «Фигура называется симметричной относительно прямой m, если для каждой точки фигуры симметричная ей точка относительно прямой, м также принадлежит этой фигуре. Прямая м называется осью симметрии фигуры». Тогда говорят, что фигура обладает осевой симметрией.

В более узком смысле осью симметрии называют ось симметрии второго порядка и говорят об «осевой симметрии», которую можно определить так: фигура (или тело) обладает осевой симметрией относительно некоторой оси, если каждой её точке С, соответствует такая принадлежащая этой же фигуре точка Д, что отрезок АВ перпендикулярен к оси, пересекает её и в точке пересечения делится пополам.

Приведём примеры фигур, обладающих осевой симметрий. У неразвёрнутого угла одна ось симметрии ― прямая, на которой расположена биссектриса угла.

Равнобедренный (но не равносторонний) треугольник имеет также одну ось симметрии. Прямоугольник и ромб, не являющиеся квадратами, имеют по две оси, а квадрат ― четыре оси симметрии. У окружности их бесконечно много ― любая прямая, проходящая через её центр, является осью симметрии. Имеются фигуры, у которых нет ни одной оси симметрии. К таким фигурам относятся параллелограмм, отличный от прямоугольника, разносторонний треугольник.(слайд 13)

2.3. Зеркальная симметрия

Зеркальной симметрией называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей относительно плоскости а точку М1.

Зеркальная симметрия хорошо известна каждому человеку из повседневного наблюдения. Как показывает само название, зеркальная симметрия связывает любой предмет и его отражение в плоском зеркале. Говорят, что одна фигура (или тело) зеркально симметрично другой, если вместе они образуют зеркально симметричную фигуру (или тело).

Многие очень любят фотографировать природу. Особенно когда весной разливается река, то на дальних лугах можно увидеть красивую картину, когда в воде отражаются: облака, трава.

Игрокам в бильярд издавна знакомо действие отражения. Их «зеркала» - это борта игрового поля, а роль луча света исполняют траектории шаров. Ударившись о борт возле угла, шар катится к стороне, расположенной под прямым углом, и, отразившись от неё, движется обратно параллельно направлению первого удара.

Важно отметить, что два симметричных друг другу тела, не могут быть вложены или наложены друг на друга. Так перчатку правой руки нельзя надеть на левую руку. Симметрично зеркальные фигуры при всём своём сходстве существенно отличаются друг от друга. Чтобы убедиться в этом, достаточно поднести лист бумаги к зеркалу и попытаться прочесть несколько слов, напечатанных на ней, буквы и слова просто-напросто будут перевёрнуты справа налево. По этой причине симметричные предметы нельзя назвать равными, поэтому их называют зеркально равными.

Две зеркально симметричные плоские фигуры всегда можно наложить друг га друга. Однако для этого необходимо вывести одну из них (или обе) из их общей плоскости. Вообще зеркально равными телами (или фигурами) называются тела (или фигуры) в том случае, если при надлежащем их смещении они могут образовать две половины зеркально симметричного тела (или фигуры).(слайд 14)

 

2.4. Поворотная симметрия

Поворотная симметрия – это симметрия, сохраняющаяся форму предмета при повороте вокруг некоторой оси на угол, равный 360°/n (или кратный этой величине), где n = 2, 3, 4, … Указанную ось называют поворотной осью n-го порядка. (слайд 15)

При п=2 все точки фигуры поворачиваются на угол 1800 (3600 /2 = 1800 )вокруг оси, при этом форма фигуры сохраняется, т.е. каждая точка фигуры переходит в точку той же фигуры(фигура преобразуется сама в себя). Ось называют осью второго порядка.

Предмет может иметь более одной поворотной оси: рис.1 – 3оси поворота, рис.2 -4 оси, рис 3 – 5 осей, рис. 4 – только 1 ось

Всем известные буквы «И» и «Ф» обладают поворотной симметрией. Если повернуть букву «И» на 180° вокруг оси, перпендикулярной к плоскости буквы и проходящей через ее центр, то буква совместится сама с собой. Иными словами, буква «И» симметрична относительно поворота на 180°, 180°= 360° : 2, n =2 , значит она обладает симметрией второго порядка.

Заметим, что поворотной симметрией второго порядка обладает также буква «Ф».

Кроме того буква И имеет центр симметрии, а буква Ф ось симметрии.

Вернемся к примерам из жизни: стакан, конусообразный фунтик с мороженым, кусочек проволоки, труба.

Если мы повнимательней присмотримся к этим телам, то заметим, что все они, так или иначе состоят из круга, через бесконечное множество осей симметрии которого проходит бесчисленное множество плоскостей симметрии. Большинство таких тел (их называют телами вращения) имеют, конечно, и центр симметрии (центр круга), через который проходит по меньшей мере одна поворотная, ось симметрии.

Отчетливо видна, например, ось у конуса фунтика с мороженым. Она проходит от середины круга (торчит из мороженого!) до острого конца конуса-фунтика. Совокупность элементов симметрии какого-либо тела мы воспринимаем как своего рода меру симметрии. Шар, без сомнения, в отношении симметрии является непревзойденным воплощением совершенства, идеалом. Древние греки воспринимали его как наиболее совершенное тело, а круг, естественно, как наиболее совершенную плоскую фигуру.

 

                                      Глава II. Симметрия в природе.

1. Значение симметрии в познании природы

Идея симметрии часто являлась основным пунктом в гипотезах и теориях учёных прошлого. Вносимая симметрией упорядоченность проявляется, прежде всего, в ограничении многообразия возможных структур, в сокращении числа возможных вариантов. В качестве важного физического примера можно провести факт существования определяемых симметрией ограничений разнообразия структур молекул и кристаллов. Поясним эту мысль на следующем примере. Допустим, что в некоторой отдалённой галактике обитают высокоразвитые существа, увлекающиеся среди прочих занятий также играми. Мы можем ничего не знать о вкусах этих существ, о строении их тела и особенностях психики. Однако, достоверно, что игральные кости имеют одну из пяти форм — тетраэдр, куб, октаэдр, додекаэдр, икосаэдр. Всякая иная форма игральной кости в принципе исключена, поскольку требование равно вероятности выпадения при игре любой грани предопределяет использование формы правильного многогранника, а таких форм только пять.

Идея симметрии часто служила учёным путеводной нитью при рассмотрении проблем мироздания. Наблюдая хаотическую россыпь звё1зд на ночном небе, мы понимаем, что за внешним хаосом скрываются вполне симметричные спиральные структуры галактик, а в них — симметричные структуры планетных систем. Симметрия внешней формы кристалла является следствием её внутренней симметрии — упорядоченного взаимного расположения в пространстве атомов (молекул). Иначе говоря, симметрия кристалла связана с существованием пространственной решётки из атомов, так называемой кристаллической решётки.

Согласно современной точке зрения, наиболее фундаментальные законы природы носят характер запретов. Они определяют, что может, а что не может происходить в природе. Так, законы сохранения в физике элементарных частиц являются законами запрета. Они запрещают любое явление, при котором изменялась бы «сохраняющая величина», являющаяся собственной «абсолютной» константой (собственным значением) соответствующего объекта и характеризующая его «вес» в системе других объектов. И эти значения являются абсолютными до тех пор, пока такой объект существует.

В современной науке все законы сохранения рассматриваются именно как законы запрета. Так, в мире элементарных частиц многие законы сохранения получены как правила, запрещающие те явления, которые никогда не наблюдаются в экспериментах.

Видный советский ученый академик В. И. Вернадский писал в 1927 году: «Новым в науке являлось не выявление принципа симметрии, а выявление его всеобщности». Действительно, всеобщность симметрии поразительна. Симметрия устанавливает внутренние связи между объектами и явлениями, которые внешне никак не связаны.

Всеобщность симметрии не только в том, что она обнаруживается в разнообразных объектах и явлениях. Всеобщим является сам принцип симметрии, без которого по сути нельзя рассмотреть ни одной фундаментальной проблемы, будь то проблема жизни или проблема контактов с внеземными цивилизациями.

Принципы симметрии лежат в основе теории относительности, квантовой механики, физики твёрдого тела, атомной и ядерной физики, физики элементарных частиц. Эти принципы наиболее ярко выражаются в свойствах инвариантности законов природы. Речь при этом идёт не только о физических законах, но и о других, например, биологических.

Примером биологического закона сохранения может служить закон наследования. В основе его лежат инвариантность биологических свойств по отношению к переходу от одного поколения к другому. Вполне очевидно, что без законов сохранения (физических, биологических и прочих) наш мир попросту не смог бы существовать.

Следует выделить аспекты, без которых симметрия невозможна:

·       объект — носитель симметрии; в роли симметричных объектов могут выступать вещи, процессы, геометрические фигуры, математические выражения, живые организмы и т.д.

·       некоторые признаки — величины, свойства, отношения, явления — объекты, которые при преобразованиях симметрии остаются неизменными; их называют инвариантными.

·       свойство объекта превращаться по выделенным признакам в самого себя после соответствующих изменений.

Важно подчеркнуть, что инвариант вторичен по отношению к изменению; покой относителен, движение абсолютно.

Таким образом, симметрия выражает сохранение чего-то при каких-то изменениях или сохранение чего-то несмотря на изменение. Симметрия предполагает неизменность не только самого объекта, но и каких-либо его свойств по отношению к преобразованиям, выполненным над объектом. Неизменность тех или иных объектов может наблюдаться по отношению к разнообразным операциям — к поворотам, переносам, взаимной замене частей, отражениям и т.д. В связи с эти выделяются разные типы симметрии.

ПОВОРОТНАЯ СИММЕТРИЯ. Говорят, что объект обладает поворотной симметрией, если он совмещается сам с собой при повороте на угол 2/n, где n может равняться 2, 3, 4 и т.д. до бесконечности. Ось симметрии называется осью n-ного порядка.

ПЕРЕНОСНАЯ (ТРАНСЛЯЦИОННАЯ) СИММЕТРИЯ. О такой симметрии говорят тогда, когда при переносе фигуры вдоль прямой на какое-то расстояние, а либо расстояние, кратное этой величине, она совмещается сама с собой. Прямая, вдоль которой производится перенос, называется осью переноса, а расстояние - элементарным переносом или периодом. С данным типом симметрии связано понятие периодических структур или решёток, которые могут быть и плоскими, и пространственными.

ЗЕРКАЛЬНАЯ СИММЕТРИЯ. Зеркально симметричным считается объект, состоящий из двух половин, которые являются зеркальными двойниками по отношению друг к другу. Трёхмерный объект преобразуется сам в себя при отражении в зеркальной плоскости, которую называют плоскостью симметрии. [13]

Достаточно взглянуть на окружающий нас реальный мир, чтобы убедиться в первостепенном значении именно зеркальной симметрии с соответствующим симметричным элементом — плоскостью симметрии. В самом деле, форма всех объектов, которые двигаются по земной поверхности или возле неё — шагают, плывут, летят, катятся, - обладает, как правило, одной более или менее хорошо выраженной плоскостью симметрии. Всё то, что развивается или движется лишь в вертикальном направлении, характеризуется симметрией конуса, то есть имеет множество плоскостей симметрии, пересекающихся вдоль вертикальной оси. И то и другое объясняется действием силы земного тяготения, симметрия которого моделируется конусом.

СИММЕТРИИ ПОДОБИЯ. Симметрия представляющая собой своеобразные аналоги предыдущих симметрией с той лишь разницей, что они связаны с одновременным уменьшением или увеличением подобных частей фигуры и расстояний между ними. Простейшим примером такой симметрии являются матрёшки. Иногда фигуры могут обладать разными типами симметрии. Например, поворотной и зеркальной обладают некоторые буквы: Ж, Н, Ф, О, Х.

Существует много других видов симметрий, имеющих абстрактный характер.

Например, ПЕРЕСТАНОВОЧНАЯ СИММЕТРИЯ, которая состоит в том, что если тождественные частицы поменять местами, то никаких изменений не происходит;

 НАСЛЕДСТВЕННОСТЬ — это тоже определённая симметрия.

КАЛИБРОВОЧНЫЕ СИММЕТРИИ связаны с изменением масштаба.

В неживой природе симметрия, прежде всего, возникает в таком явлении природы, как кристаллы, из которых состоят практически все твёрдые тела.

Именно она и определяет их свойства. Самый очевидный пример красоты и совершенства кристаллов — это известная всем снежинка.

Внимательное наблюдение показывает, что основу красоты многих форм, созданных природой, составляет симметрия.

2. Симметрия в живой природе. Асимметрия и симметрия

Наиболее часто встречающиеся типы симметрии в живой природе:

В живой природе наиболее часто встречается симметрия зеркального отражения и радиальная симметрия. Радиальная симметрия — это ось симметрии бесконечного порядка. Ещё древние греки обратили внимание на этот факт.

Симметрией обладают объекты и явления живой природы. Она не только радует глаз и вдохновляет поэтов всех времён и народов, а позволяет живым организмам лучше приспособиться к среде обитания и просто выжить.

В живой природе огромное большинство живых организмов обнаруживает различные виды симметрии (формы, подобия, относительного расположения). Причём организмы разного анатомического строения могут иметь один и тот же тип внешней симметрии.

Внешняя симметрия может выступить в качестве основания классификации организмов (сферическая, осевая, радиальная и т.д.). Микроорганизмы, живущие в условиях слабого воздействия гравитации, имеют ярко выраженную симметрию формы.

Асимметрия присутствует уже на уровне элементарных частиц и проявляется в абсолютном преобладании в нашей Вселенной частиц над античастицами. Известный физик Ф. Дайсон писал: «Открытия последних десятилетий в области физики элементарных частиц заставляет нас обратить особое внимание на концепцию нарушения симметрии. Развитие Вселенной с момента её зарождения выглядит как непрерывная последовательность нарушений симметрии. В момент своего возникновения при грандиозном взрыве Вселенная была симметрична и однородна. По мере остывания в ней нарушается одна симметрия за другой, что создаёт возможности для существования всё большего и большего разнообразия структур. Феномен жизни естественно вписывается в эту картину.  Жизнь ― это тоже нарушение симметрии».

Молекулярная асимметрия открыта Л. Пастером, который первым выделил «правые» и «левые» молекулы винной кислоты: правые молекулы похожи на правый винт, а левые ― на левый. Такие молекулы химики называют стереоизомерами.

Молекулы стереоизомеры имеют одинаковый атомный состав, одинаковые размеры, одинаковую структуру ― в то же время они различны, поскольку являются зеркально асимметричными, т.е. Объект оказывается не тождественным со своим зеркальным двойником. Поэтому здесь понятия «правый ― левый» условны.

В настоящее время хорошо известно, что молекулы органических веществ, составляющие основу живой материи, имеют асимметричный характер, т.е. В состав живого вещества они входят только либо как правые, либо как левые молекулы. Таким образом, каждое вещество может входить в состав живой материи только в том случае, если оно обладает вполне определённым типом симметрии. Например, молекулы всех аминокислот в любом живом организме могут быть только левыми, сахара ― только правыми. Это свойство продуктов вещества и его продуктов жизнедеятельности называют диссиметрией. Оно имеет совершенно фундаментальный характер. Хотя правые и левые молекулы неразличимы по химическим свойствам, живая материя их не только различает, но и делает выбор. Она отбраковывает и не использует молекулы, не обладающие нужной ей структурой. Как это происходит, пока не ясно. Молекулы противоположной симметрии для неё ― яд.

Если бы живое существо оказалось в условиях, когда вся пища была бы составлена из молекул противоположной симметрии, не отвечающей диссиметрии этого организма, то оно погибло бы от голода. В неживом веществе правых и левых молекул поровну.

Диссиметрия ― единственное свойство, благодаря которому мы можем отличать вещество биогенного происхождения от неживого вещества. Мы не можем ответить на вопрос, что такое жизнь, но имеем способ отличить живое от неживого. Таким образом, асимметрию можно рассматривать как разграничительную линию между живой и неживой природой. Для неживой материи характерно преобладание материи, при переходе от неживой к живой материи уже на микроуровне преобладает асимметрия. В живой природе асимметрию можно увидеть всюду. Очень удачно это подметил в романе «Жизнь и судьба» В. Гроссман: «В большом миллионе русских деревенских изб, нет, и не может быть неразличимо схожих. Всё живое ― неповторимо».[3]

Симметрия лежит в основе вещей и явлений, выражая нечто общее, свойственно разным объектам, тогда как асимметрия связана с индивидуальным воплощением общего в конкретном объекте. На принципе симметрии основан метод аналогий, предполагающий отыскание общих свойств в различных объектах На основе аналогий создаются физические модели различных объектов и явлений. Аналогии между процессами позволяют описывать их общими уравнениями.

ОБЩАЯ ФОРМУЛА СИММЕТРИИ В БИОЛОГИИ

Рассмотрим тела, обладающие четырьмя плоскостями симметрии, пересекающимися на оси четвёртого порядка. Симметрию таких тел можно обозначить так: 4۰t.

Общая формула симметрии таких фигур записывается в виде: N۰t, где N — символ оси, t — символ плоскости, t может быть равно 1, 2, 3... .

В биологии симметрия N ۰t называется радиальной (из-за целого веера пересекающихся на оси плоскостей)

Билатеральная система — частный случай радиальной, так как в этом случае N=1 ۰t.

 

 

 

 

3. Симметрия растений

Центральная симметрия образуется при повороте вокруг точки на угол 180^0. Ярко выраженной центральной симметрией обладают цветы и плоды растений.

Изображения на плоскости многих предметов окружающего нас мира имеют ось симметрии или центр симметрии. Многие листья деревьев и лепестки цветов симметричны относительно среднего стебля. Симметрию можно увидеть и на листьях деревьев. (слайд 18)

Симметрию можно увидеть среди цветов. Осевой симметрией обладают цветы семейства розоцветных, а центральной симметрией — семейство крестоцветных.

Среди цветов наблюдаются поворотные симметрии разных порядков. Многие цветы обладают характерным свойством: цветок можно повернуть так, что каждый лепесток займёт положение соседнего, цветок же совместится с самим собой. Такой цветок обладает осью симметрии. Минимальный угол, на который нужно повернуть цветок вокруг оси симметрии, чтобы он совместился с самим собой, называется элементарным углом поворота оси. Этот угол для различных цветов не одинаков. Для ириса он равен 120 градусов, для колокольчика — 72 градуса, для нарцисса — 60 градусов. Поворотную ось можно характеризовать и с помощью другой величины, называемой порядком оси и показывающей, сколько раз произойдёт смещение при повороте на 360 градусов. Те же цветы нарцисса, колокольчика и нарцисса обладают осями третьего, пятого и шестого порядков соответственно.

Особенно часто среди цветов встречается симметрия пятого порядка. К ней относятся такие полевые цветы как колокольчик, незабудка, зверобой, лапчатка гусиная и др.; цветы плодовых растений — вишня, яблоня, груша, мандарин и др.; цветы плодово-ягодных растений — земляника, ежевика, малина, шиповник и др.; садовые цветы — настурция, флокс и др.

В пространстве существуют тела, обладающие винтовой симметрией, т.е. Совмещающиеся со своим первоначальным положением после поворота на угол поворота вокруг оси, дополненного сдвигом той же оси.

Винтовая симметрия наблюдается в расположении листьев на стеблях большинства растений. Располагаясь винтом по стеблю, листья как бы раскидываются во все стороны и не заслоняют друг друга от света, крайне необходимого для жизни растений. Это интересное ботаническое явление носит название филлотаксиса, что буквально означает строение листа. Другим проявлением филлотаксиса оказывается устройство соцветия подсолнечника или чешуи еловой шишки, в которой чешуйки располагаются в виде спиралей и винтовых линий. Такое расположение особенно чётко видно у ананаса, имеющего более или менее шестиугольные ячейки, которые образуют ряды, идущие в различных направлениях.

Специфика строения растений и животных определяется особенностями среды обитания, к которой они приспосабливаются, особенностями их образа жизни. У любого древа есть основание и вершина, «верх» и «них», выполняющие различные функции. Значимость различия верхней и нижней частей, а также направление силы тяжести определяют вертикальную ориентацию поворотной оси «древесного конуса» и плоскостей симметрии.

Для листьев характерна зеркальная симметрия. Эта же симметрия встречается и у цветов, однако у них зеркальная симметрия чаще выступает в сочетании с поворотной симметрией. Нередки случаи и переносной симметрии (веточки акации, рябины). Интересно, что в цветочном мире наиболее распространена поворотная симметрия пятого порядка, которая принципиально невозможна в периодических структурах неживой природы. Этот факт академик Н. Белов объясняет тем, что ось пятого порядка — своеобразный инструмент борьбы за существование, «страховка против окаменения, кристаллизации, первым шагом которой была бы их поимка решёткой». Действительно, живой организм не имеет кристаллического строения в том смысле, что даже отдельные его органы не обладают пространственной решёткой. Однако, упорядоченные структуры в ней представлены очень широко.

Соты — настоящий конструкторский шедевр. Они состоят из ряда шестигранных ячеек. Это самая плотная упаковка, позволяющая наивыгоднейшим образом разместить в ячейке личинку и при максимальном возможном объёме наиболее экономно использовать строительный материал -  воск

4. Симметрия животных

 

Внимательное наблюдение обнаруживает, что основу красоты многих форм, созданных природой, составляет симметрия, точнее, все её виды — от простейших до самых сложных. Симметрия в строении животных — почти общее явление, хотя почти всегда встречаются исключения из общего правила.

Под симметрией у животных понимают соответствие в размерах, форме и очертаниях, а также относительное расположение частей тела, находящихся на противоположных сторонах разделяющей линии. Строение тела многих многоклеточных организмов отражает определённые формы симметрии, такие как радиальную (лучевую) или билатеральную (двустороннюю), которые являются основными типами симметрии. Кстати, склонность к регенерации (восстановление) зависит от типа симметрии животного. ( слайд 19)

В биологии о радиальной симметрии идёт речь, когда через трёхмерное существо проходят или более плоскости симметрии. Эти плоскости пересекаются в прямой. Если животное будет вращаться вокруг оси на определённый градус, то оно будет отражаться само на себе. В двухмерной проекции радиальная симметрия может сохраняться, если ось направлена перпендикулярно к проекционной плоскости. Иными словами, сохранение радиальной симметрии зависит от угла наблюдения.

При радиальной или лучистой симметрии тело имеет форму короткого или длинного цилиндра либо сосуда с центральной осью, от которого отходят в радиальном порядке части тела. Среди них встречается так называемая пентасимметрия, базирующаяся на пяти плоскостях симметрии.

Радиальная симметрия характерна для многих стрекающих, а также для большинства иглокожих, кишечнополостных. Взрослые формы иглокожих приближаются к радиальной симметрии, в то время как их личинки билатерально симметричны.

Лучевую симметрию мы также видим у медуз, кораллов, актиний, морских звёзд. Если вращать их вокруг собственной оси, они несколько раз «совместятся сами с собой». Если отрезать у морской звезды любое из пяти щупалец, оно сумеет восстановить всю звезду. От радиальной симметрии различаются двулучевая радиальная симметрия (две плоскости симметрии, к примеру, гребневики), а также билатеральная симметрия (одна плоскость симметрии, к примеру, двусторонне-симметричные).

При билатеральной симметрии осей симметрии три, но симметричных сторон только одна пара. Потому что две другие стороны — брюшная и спинная — друг на друга не похожи. Этот вид симметрии характерен для большинства животных, в том числе насекомых, рыб, земноводных, рептилий, птиц, млекопитающих. Например, черви, членистоногие, позвоночные. У большинства многоклеточных (у человека в том числе) другой тип симметрии — двусторонняя. Левая половина их тела - это как бы «отражённая в зеркале правая». Этот принцип, однако, не относится к отдельным внутренним органам, что демонстрирует, например, расположение печени или сердца у человека. Плоский червь планария имеет двустороннюю симметрию. Если разрезать его вдоль оси тела или поперёк, из обеих половинок вырастут новые черви. Если же измельчить планарию как-нибудь иначе — скорее всего ничего не выйдет.

Типы симметрии у животных:

1.     центральная

2.     осевая

3.     радиальная

4.     билатеральная

5.     двулучевая

6.     поступательная (метамерия)

7.     поступательно-вращательная

Ось симметрии — это ось вращения. В этом случае у животных, как правило, отсутствует центр симметрии. Тогда вращение может происходить только вокруг оси. При этом ось чаще всего имеет разнокачественные полюса. Например, у кишечнополостных, гидры  или актинии, на одном полюсе расположен рот, на другом — подошва, которой эти неподвижные животные прикреплены к субстрату. Ось симметрии может совпадать морфологически с переднезадей осью тела.

Плоскость симметрии — это плоскость, проходящая через ось симметрии, совпадающая с ней и рассекающая тело на две зеркальные половины. Эти половины, расположенные друг против друга, называют антимерами (anti — против; mer — часть). Например, у гидры плоскость симметрии должна пройти через ротовое отверстие и через подошву. Антимеры противоположных половин должны иметь ровное количество щупалец, расположенных вокруг рта гидры. У гидры можно провести несколько плоскостей симметрии, число которых будет кратно числу щупалец. У актиний с очень большим числом щупалец можно провести много плоскостей симметрии. У медузы с четырьмя щупальцами на колоколе число плоскостей симметрии будет ограничено числом, кратным четырём. У гребневиков только две плоскости симметрии -глоточная и щупальцевая. Наконец, у двусторонне-симметричных организмов только одна плоскость и только две зеркальные антимеры — соответственно правая и левая стороны животного.

Можно сказать также, что каждое животное (будь то насекомое, рыба или птица) состоит из двух анантиоморфов — правой и левой половин. Анантиоморфы — пара зеркально асимметричных объектов (фигур), являющихся зеркальным изображением один другого (например, пара перчаток). Иными словами — это объект и его зазеркальный двойник при условии, что сам объект зазеркально асимметричен.

Сферическая симметрия имеет место у радиолярий и солнечников, тело которых сферической формы, а его части распределены вокруг центра сферы и отходят от неё. У таких организмов нет ни передней, ни задней, ни боковых частей тела, любая плоскость, проведённая через центр, делит животное на одинаковые половинки.

5.Человек – существо симметричное

Не станем пока разбираться, существует ли на самом деле абсолютно симметричный человек. У каждого, разумеется, обнаружится родинка, прядь волос или какая-нибудь другая деталь, нарушающая внешнюю симметрию. Левый глаз никогда не бывает в точности таким, как правый, да и уголки рта находятся на разной высоте, во всяком случае, у большинства людей. И всё же это лишь мелкие несоответствия. Никто не усомнится, что внешне человек построен симметрично: левой руке всегда соответствует правая и обе руки совершенно одинаковы!  Если бы наши руки и в самом деле были совершенно одинаковы, мы могли бы в любой момент поменять их. Было бы возможно, скажем, путём трансплантации пересадить левую ладонь на правую руку, или, проще, левая перчатка подходила бы тогда к правой руке, но на самом деле это не так. Каждому известно, что сходство между нашими руками, ушами, глазами и другими частями тела такое же, как между предметом и его отражением в зеркале. Многие художники обращали пристальное внимание на симметрию и пропорции человеческого тела, во всяком случае, до тех пор, пока ими руководило желание в своих произведениях как можно точнее следовать природе.(слайд 20)

Известны каноны пропорций, составленные Альбрехтом Дюрером и Леонардо да Винчи. Согласно этим канонам, человеческое тело не только симметрично, но и пропорционально. Леонардо открыл, что тело вписывается в круг и в квадрат. Дюрер занимался поисками единой меры, которая находилась бы в едином соотношении с длиной туловища или ноги (такой мерой он считал длину руки до локтя). В современных школах живописи в качестве единой меры чаще всего принимается размер головы по вертикали. С известным допущением можно считать, что длина туловища превосходит размер головы в восемь раз. На первый взгляд это кажется странным. Но нельзя забывать, что большинство высоких людей отличаются удлинённым черепом и, наоборот. Размеру головы пропорциональна не только длина туловища, но и размеры других частей тела. По этому принципу построены все люди, оттого-то мы, в общем, похожи друг на друга. Однако, наши пропорции согласуются лишь приблизительно, а потому люди лишь похожи, но неодинаковы. Во всяком случае, все мы симметричны! К тому же некоторые художники в своих произведениях особенно подчёркивают эту симметрию. И в одежде человек тоже, как правило, старается поддерживать впечатление симметричности: правый рукав соответствует левому, левая штанина — правой. Пуговицы на куртке или рубашке сидят ровно посередине, а если и отступают от неё, то на симметричные расстояния. Но на фоне этой общей симметрии в мелких деталях мы умышленно допускаем асимметрию, например, расчёсывая волосы на косой пробор — слева или справа или делая асимметричную стрижку. Или, скажем, помещая на костюме асимметричный кармашек на груди. Или, надев кольцо на безымянный палец только одной руки. Лишь на одной стороне груди носятся ордена и значки. Полная безукоризненная симметрия выглядела бы нестерпимо скучно.  Именно небольшие отклонения от неё и придают индивидуальные, характерные черты. И вместе с тем порой человек старается подчеркнуть, усилить различие между левым и правым. В средние века мужчины одно время щеголяли в панталонах со штанинами разных цветов (например, в одной — красной, а в другой — чёрной или белой). В не столь отдалённые дни были популярны джинсы с яркими заплатами или цветными разводами. Но подобная мода всегда недолговечна.  Лишь тактичные, скромные отклонения от симметрии остаются на долгие времена.

 

Результаты опроса

1.Как часто вы встречали симметрию в живой природе?(слайд 22)

Часто	Редко, но бывает	Очень редко	Не обращали внимание
22%	40%	3%	35%

 

 

2.Сколько видов симметрии вы знаете?(слайд 23)

Не одного	1 вид	2 вида	3 вида	4 вида
9%	0%	0%	4%	87%

 

3.Приведите пример зеркальной симметрии.  (слайд 24)

Затрудняюсь ответить	Бабочка	Улитка	Кузнечик	Черепаха	Отражение
13%	37%	7%	4%	4%	35%

                                                    ЗАКЛЮЧЕНИЕ

  

   С симметрией мы встречаемся везде — в природе, технике, искусстве, науке. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Принципы симметрии играют важную роль в физике, математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. Законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, подчиняются принципам симметрии. Существует множество видов симметрии, как в растительном, так и в животном мире, но при всём многообразии живых организмов, принцип симметрии действует всегда, и этот факт еще раз подчёркивает гармоничность нашего мира. Ещё одним интересным проявлением симметрии являются биологические ритмы (биоритмы), циклические колебания биологических процессов и их характеристик (сокращения сердца, дыхание, колебания интенсивности деления клеток, обмена веществ, двигательной активности, численности растений и животных), зачастую связанные с приспособлением организмов к геофизическим циклам. Исследованием биоритмов занимается особая наука — хронобиология. Помимо симметрии существует также понятие асимметрии. Симметрия лежит в основе вещей и явлений, выражая нечто общее, свойственное разным объектам, тогда как асимметрия связана с индивидуальным воплощением этого общего в конкретном объекте. Симметрия окружает человека на каждом шагу. В природе и во многих творениях человека без симметрии не было бы красоты, совершенства и удобства. Как бы мы жили без симметрии? Неужели лишь она украшает наш мир? Да, без симметрии наш мир выглядел бы совсем по-другому. Ведь именно на симметрии основаны многие законы сохранения. Например, законы сохранения энергии, импульса и момента импульса являются следствиями пространственно-временных симметрий. И без симметрии не было бы законов сохранения, которые во многом управляют нашим миром.

ТАК ЧТО СИММЕТРИЯ — ОДНО ИЗ ГЛАВНЫХ ПОНЯТИЙ ВО ВСЕЛЕННОЙ!

 

                                           

 Список литературы

1. Атанасян, Л. С. Бутузов В. Ф. «Геометрия 10 — 11 класс»

 

2. Вейль, Г.«Симметрия» Москва

 

3. Виленкин, З. Н. «Симметрия в природе и технике» М.: Едиториал УРСС

 

4. Выгодский, М. Я «Справочник по элементарной математике»

 Издательство «Наука». – Москва

 

5. Гика М. «Эстетика пропорций в природе и искусстве» Москва

 

6. Гильде, В.«Зеркальный мир» Мир

7. Даль, В. И. «Толковый словарь живого великорусского языка» Москва

8. Ожегов, С. И. Толковый словарь русского языка /   Ожегов, С. И.,. Шведова, Н. Ю – М.: Просвещение, 2010.Емельянов В. «Фундаментальные симметрии»МИФИ, 2008 г.

 

9. Тарасов, С Л. «Этот удивительно симметричный мир»  Издательство: - М.: Просвещение

 

10. Тарасов, С. Л«Симметрия в окружающем мире» ОНИКС, 2005 г

 

11. http://www.worldnatures.ru 

 

12. https://ru.wikipedia.org/wiki

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Скачано с www.znanio.ru