Индивидуальный проект по информатике на тему: «История развития вычислительной техники»

МИНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ПЕРЕСНЯНСКАЯ СРЕДНЯЯ ШКОЛА

ПОЧИНКОВСКИЙ РАЙОН

СМОЛЕНСКАЯ ОБЛАСТЬ

 

 

Индивидуальный проект по информатике на тему:

«История развития вычислительной техники»

 

 

 

 

 

Выполнил работу

Ученик 9 класса

Якуненков   Александр

Руководитель

Яковлева    Анна Александровна

Учитель – консультант

Миренкова Светлана Александровна

 

 

 

 

Работа допущена к защите «____» _____________ 202 __ года

Подпись руководителя проекта __________ ________________________

 

Пересна

2021 год

 

Оглавление

 

 

Введение

Основная часть

1. Ручной этап развития ВТ

1.1. Пальцевый счет

1.2. Фиксированный счет. Абак. Счеты

1.3. Десятичная система счисления

 2. Механический этап развития ВТ 

3. Электромеханический этап развития вычислительной техники

4. Электронная эпоха

5. Суперкомпьютеры

Заключение

Список литературы

Приложение 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Введение

 

 

В настоящее время информатика и ее практические результаты становятся важнейшим двигателем научно-технического прогресса и развития человеческого общества. Скорость развития информатики поразительна, в истории человечества этому бурно развивающемуся процессу нет аналога. Теперь уже очевидно, что 21 век – это век максимального использования достижений информатики в экономике, политике, науке, образовании, медицине, быту, военном деле и т. д.

Как нам всем известно, компьютер — это устройство или система, способная выполнять заданную, чётко определённую, изменяемую последовательность операций. Это чаще всего операции численных расчётов и манипулирования данными, однако, сюда относятся и операции ввода-вывода. Описание последовательности операций называется программой. Сегодня мы поговорим о влиянии компьютеров и других устройств в современном мире. Оценим масштабы компьютеризации и узнаем, как выглядели, и какие функции выполняли первые модели вычислительных машин. На мой взгляд, актуальность данной темы на сегодняшний день имеет особое значение, так как мы живём в мире, где без телефона и любого другого устройства жизнь нам кажется уже не такой насыщенной. И как мы все прекрасно понимаем, создание новых технологий не останавливается ни на минуту.

 Актуальность  проекта заключается в том, что человек XXI века, активно стремиться использовать все плоды научных разработок цивилизации, в частности - компьютер и Интернет. Сегодня всемирная сеть является неотъемлемой частью жизни современного человека, компьютерами пользуются все и везде. Люди осваивают многие программы и услуги, размещенные в сети и предназначенные для ПК. Однако немногие осведомлены об истории создания вычислительной техники. Поэтому выбранная тема является очень актуальной, так как служит благородной цели - просвещению пользователей и углублению их знаний о том, с чем они сталкиваются ежедневно.

История создания средств цифровой вычислительной техники уходит в глубь веков. Она увлекательна и поучительна, с нею связаны имена выдающихся ученых мира. 

Компьютеры проникли во все сферы деятельности человека, начиная с начального образования и заканчивая изучением новейших технологий, изучения новых видов материи, неизвестных пока человечеству. 

Объект исследования: вычислительная техника

Предмет исследования: история вычислительной техники

Цель: исследовать вычислительную технику по мере её развития

Задачи. Изучить:

- хронологию возникновения вычислительной техники

- кем было изобретено устройство

- где использовалась та или иная вычислительная техника

- из чего состояло устройство

- вычислительные свойства техники

Гипотеза. По мере развития вычислительной техники она становится более удобной для человека, то есть меньших размеров и при этом более быстрой.

 

 

 

 

 

 

 

 

 

1. Ручной этап развития ВТ

1.1. Пальцевый счёт

 

 

Ручной период автоматизации вычислений начался на заре человеческой цивилизации (период от 50 тысячелетия до н.э. и до XVII века) и базировался на использовании различных частей тела, в первую очередь, пальцев рук и ног (Приложение Рис. 1).

Древние египтяне полагали, что в загробном миру душу умершего подвергают экзамену по счету на пальцах. Они научились даже умножать на пальцах однозначные числа от 6 до 9. Для этого на одной руке вытягивали столько пальцев, на сколько первый множитель превосходит число 5, а на второй делали то же самое для второго множителя. Остальные пальцы загибали. Потом бралось число вытянутых пальцев и умножалось на 10, далее перемножались числа, показывавшие, сколько загнуто пальцев на руках. К числу вытянутых пальцев, умноженному на 10, добавлялось полученное произведение.

В дальнейшем пальцевой счет был усовершенствован, и с помощью пальцев научились показывать числа до 10 000. А китайские купцы торговались, взяв друг друга за руки и указывая цену нажатием на определенные суставы пальцев.

Североевропейский пальцевой счет позволял показывать пальцами одной руки, складываемыми в различные комбинации, все числа от 1 до 100. Причем большим и указательным пальцами изображались десятки, остальными тремя - единицы. Например, число 30 получалось, когда большой и указательный пальцы левой руки были соединены в кольцо. Для того чтобы изобразить число 60, большой палец нужно согнуть и как бы склонить его перед указательным, нависающим над ним. Чтобы показать число 100, нужно было прижать выпрямленный большой палец снизу к указательному и отвести остальные три пальца в сторону.

В древнерусской нумерации единицы назывались «перстами», десятки – «суставами», а все остальные числа – «сочислениями». Счет парами вплоть до середины XVIII века всегда занимал важное место в жизни россиян, поскольку имел качественное происхождение - пара рук, ног, глаз и пр. Недаром говорили: «два сапога – пара», «двугривенный» и т.д.

Четверичная система счета основана на «перстах» руки, не считая большого пальца. Большой - вовсе не «перст», он «палесъ»! - в этой системе счисления означал конец счета, то есть являлся эквивалентом нуля.

Счет восьмерками также основан на пальцевом счете и, по сути, является сочетанием двоичной и четверичной систем. Элементы восьмеричной системы существовали на Руси еще в начале XX столетия. Это и восьмиконечный крест, который использовали староверы, и восьмиголосное церковное пение, и название русской питейной меры - "осьмушки", получаемой в результате последовательного троекратного деления пополам.

В русской народной метрологии - это вообще деление какой-либо учетной нераздельной меры (например, куска пахотной земли, сажени или ведра вина) на части, соответствующие 1/2,1/4 и 1/8 долям.

Пальцевой счет девятками является, пожалуй, самым распространенным русским народным способом умножения на пальцах с помощью, так называемых девятериц - своеобразной таблицы умножения, обозначающей девятилетние сроки человеческой жизни. Наши предки в древности какое-то время считали девятками (впрочем, похоже, что они все-таки считали восьмерками, а с девяти начинался уже новый отрезок счета). С тех пор прошло не менее семи - девяти столетий, но мы до сих пор трепещем перед грозным «девятым валом» или устраиваем поминки по усопшему на девятый день после кончины.

 В Древней Руси (особенно в Новгородской республике XII-XV веков) был широко распространен счет, основанный на счислении числа фаланг на руке «счетовода». Счет начинался с верхней фаланги «перстка» (мизинца) левой руки, а заканчивался нижней фалангой («низ перста») указательного пальца. Большой, или «палесъ великий», левой руки при этом последовательно осуществлял «подсчет» суставов на растопыренной пятерне. Досчитав до двенадцати, «счетовод» обращался к своей правой руке и загибал на ней один палец. Так продолжалось до тех пор, пока все пальцы правой руки не оказывались сжатыми в кулак (поскольку число фаланг на четырех пальцах было равно 12, получалось 12 пятерок, то есть 60). Кулак в данном случае символизировал пятерку дюжин, то есть «шестьдесят».

Счет сороками (или «сороковицами») имел преимущественное распространение в Древней Руси. Число 40 (четыре десятка) долгое время называли «четыредцать» или «четыредесят». Число 40 на Руси когда-то играло особую роль при пальцевом счете, об этом говорят некоторые поверья. Так, сорок первый медведь считался роковым для российского охотника, убить паука - означало избавиться от сорока грехов и т.д.

Все то количество, которое превышало некое множество (например, «сорок»), превосходящее всякое воображение («сорок сороков») и не умещавшееся в голове российского землепашца из-за своей ничем не ограниченной величины, называлось одним словом – «тьма».

 

 

 

 

 

 

 

 

 

 

 

 

1.2. Фиксация счёта. Абак. Счёты

 

 

Фиксация результатов счета производилась различными способами: нанесение насечек, счетные палочки, узелки и др. Например, у народов доколумбовой Америки был весьма развит узелковый счет. Более того, система узелков выполняла также роль своего рода хроник и летописей, имея достаточно сложную структуру. Однако использование ее требовало хорошей тренировки памяти. На смену древнему счету на пальцах пришёл счёт на абаке (Приложение Рис. 2). Который впервые появился, вероятно, в Древнем Вавилоне около 3 тыс. до н. э. Доска абака была разделена на полоски. Каждая полоска назначалась для откладывания тех или иных разрядов чисел: в первую полоску ставили столько камешков или бобов, сколько в числе единиц, во вторую полоску - сколько в нем десятков, в третью - сколько сотен, и так далее. Так как у римлян камешек называли калькулюс (сравните с русским словом «галька»), то счет на абаке получил название калькуляция. И сейчас подсчет расходов называют калькуляцией, а человека, выполняющего этот подсчет - калькулятором. Но после того как два десятка лет тому назад были сделаны маленькие приборы, выполняющие за считанные секунды сложные расчеты, название «калькулятор» (Приложение Рис. 3)  перешло к ним. Один и тот же камешек на абаке мог означать и единицы, и десятки, и сотни, и тысячи - все дело лишь в том, на какой полоске он лежал. Чаще всего абаком пользовались для денежных расчетов.

В Древней Греции бытовала шутка: «Придворный похож на камешек для абака: захочет счетчик, цена ему будет целый талант, а захочет - только хальк».

Наши счеты (Приложение Рис 4)  также представляют собой абак, состоящий из рамки с укрепленными горизонтальными веревочками, на которые были нанизаны просверленные сливовые или вишневые косточки (по 10 штук).

А у китайцев на каждой проволоке не по десять шариков, а по семь. Последние два шарика отделены от первых, и каждый из них обозначает пять. Когда при расчетах набирается пять шариков, вместо них откладывают один шарик второго отделения счетов. Такое устройство китайских счетов суан-пан уменьшает необходимое число шариков.

У японцев это же устройство для счета носило название серобян. Серобян - японский абак, происходит от китайского суан-пана, который был завезен в Японию в XV - XVI веках. Серобян проще своего предшественника, у него на «небе» на один шарик меньше, чем у суан-пана.

Многовековой путь совершенствования абака привел к созданию счетного прибора законченной классической формы, используемого вплоть до эпохи расцвета клавишных настольных ЭВМ.

Счёты представляют собой раму с нанизанными на спицы костяшками. В недавнем прошлом в СССР их использовали повсеместно. Да еще и сегодня кое-где их можно встретить, помогающими в расчетных операциях.

И только появление карманных электронных калькуляторов создало реальную угрозу для дальнейшего использования русских, китайских и японских счетов - трех основных классических форм абака, сохранившихся до наших дней.

 

 

 

 

 

 

 

 

 

1.3. Позиционная система счисления

 

 

Использование абака уже предполагает наличие некоторой позиционной системы счисления, например, десятичной, троичной, пятеричной и др. Однако изобрели ее только в IX веке н.э. индийские ученые. При записи числа, в котором отсутствует какой-либо разряд (например, 101 или 1204), индийцы вместо названия цифры говорили слово «пусто». При записи на месте «пустого» разряда ставили точку, а позднее рисовали кружок. Такой кружок назывался «сунья» - на языке хинди это означало «пустое место».

Арабские математики перевели это слово по смыслу на свой язык - они говорили «сифр». Современное слово «нуль» родилось сравнительно недавно - позднее, чем «цифра». Оно происходит от латинского слова «nihil» - «никакая».

Современная десятичная позиционная система С. возникла на основе нумерации, зародившейся в Индии. До этого в Индии имелись системы С., в которых применялся не только принцип сложения, но и принцип умножения (единица какого-нибудь разряда умножается на стоящее слева число).

Аналогично строились старокитайская системы С. и некоторые другие. Если, например, условно обозначить число 3 символом III, а число 10 символом X, то число 30 запишется как IIIX (три десятка).

Такие системы С. могли служить подходом к созданию десятичной позиционной нумерации. Десятичная позиционная системы С. дает принципиальную возможность записывать сколь угодно большие числа. Запись чисел в ней компактна и удобна для производства арифметических операций. Поэтому вскоре после возникновения десятичная позиционная система С. начинает распространяться из Индии на Запад и Восток.

Арабский ученый, математик Мухаммед бен Муса ал-Хорезми (из города Хорезма на реке Аму-Дарья) в своей книге подробно описал индийскую арифметику.

Триста лет спустя (в 1120 году) эту книгу перевели на латинский язык, и она стала первым учебником «индийской» (то есть нашей современной) арифметики для всех европейских городов. Приблизительно в это же время индийские цифры начали применять и другие арабские учёные. Кроме того ал-Хорезми приблизительно в 850 году н.э. написал книгу об общих правилах решения арифметических задач при помощи уравнений. Она называлась «Китаб ал-Джебр». Эта книга дала имя науке алгебре.

 Мухаммеду бен Муса ал-Хорезми мы обязаны появлению термина «алгоритм». В первой половине XII века книга ал-Хорезми в латинском переводе проникла в Европу.Переводчик, имя которого до нас не дошло, дал ей название Algoritmi de numero Indorum («Алгоритми о счёте индийском»).

 В 9 в. появляются рукописи на арабском языке, в которых излагается эта система С., в 10 в. десятичная позиционная нумерация доходит до Испании, в начале 12 в. она появляется и в других странах Европы. Новая система С. получила название арабской, потому что в Европе с ней познакомились впервые по латинским переводам с арабского.

Только в 16 в. новая нумерация получила широкое распространение в науке и в житейском обиходе.

 В России она начинает распространяться в 17 в. С введением десятичных дробей десятинная позиционная система С. стала универсальным средством для записи всех действительных чисел.

В десятичной системе используются цифры от 0 до 10. Причем, т.к. система позиционная, положение цифр имеет значение: справа налево разряд увеличивается. Десятичная система наиболее удобна для людей во много потому, что у нас по десять пальцев на руках и ногах.

 

 

2.  Механический этап развития вычислительной техники

 

 

Развитие механики в XVII в. стало предпосылкой создания вычислительных устройств и приборов, использующих механический принцип вычислений. Такие устройства строились на механических элементах и обеспечивали автоматический перенос старшего разряда.

Эти устройства были способны выполнять уже не два, а четыре арифметических действия и назывались арифмометрами (Приложение Рис 5).

Своего рода модификацию абака предложил Леонардо да Винчи (1452-1519) в конце XV - начале XVI века. Он создал эскиз 13-разрядного суммирующего устройства с десятизубными кольцами (Приложение Рис. 6). Чертежи данного устройства были найдены среди двухтомного собрания Леонардо по механике, известного как «Codex Madrid». Это устройство что-то вроде счетной машинки в основе, которой находятся стержни, с одной стороны меньшее с другой большее, все стержни (всего 13) должны были располагаться таким образом, чтобы меньшее на одном стержне касалось большего на другом. Десять оборотов первого колеса должны были приводить к одному полному обороту второго, 10 второго к одному полному третьего и т.д.

Первая механическая машина была описана в 1623 г. профессором математики Тюбингенского университета Вильгельмом Шиккардом, реализована в единственном экземпляре и предназначалась для выполнения четырех арифметических операций над 6-разрядными числами. Машина Шиккарда (Приложение Рис. 7) содержала суммирующее и множительное устройства, а также механизм для записи промежуточных результатов. Первый блок - шестиразрядная суммирующая машина - представлял собой соединение зубчатых передач. На каждой оси имелись шестерня с десятью зубцами и вспомогательное однозубое колесо - палец. Палец служил для того, чтобы передавать единицу в следующий разряд (поворачивать шестеренку на десятую часть полного оборота, после того как шестеренка предыдущего разряда сделает такой оборот). При вычитании шестеренки следовало вращать в обратную сторону. Контроль хода вычислений можно было вести при помощи специальных окошек, где появлялись цифры. Для перемножения использовалось устройство, чью главную часть составляли шесть осей с «навернутыми» на них таблицами умножения. Использованная принципиальная схема машины Шиккарда явилась классической - она (или ее модификации) использовалась в большинстве последующих механических счетных машин вплоть до замены механических деталей электромагнитными. Однако из-за недостаточной известности машина Шиккарда и принципы ее работы не оказали существенного влияния на дальнейшее развитие вычислительной техники (ВТ), но она по праву открывает эру механической ВТ.

Первая действующая модель счетной суммирующей машины была создана в 1642 г. знаменитым французским ученым Блезом Паскалем (Приложение Рис. 8). Для выполнения арифметических операций Паскаль заменил поступательное перемещение костяшек в абаковидных инструментах на вращательное движение оси (колеса), так что в его машине сложению чисел соответствовало сложение пропорциональных им углов. Принцип действия счетчиков в машине Паскаля прост. В основе его лежит идея обыкновенной зубчатой пары - двух зубчатых колес, сцепленных между собой. Для каждого разряда имеется колесо (шестеренка) с десятью зубцами. При этом каждый из десяти зубцов представляет одну из цифр от 0 до 9. Такое колесо получило название «десятичное счетное колесо». С прибавлением в данном разряде каждой единицы счетное колесо поворачивается на один зубец, т. е. на одну десятую оборота. Требуемую цифру можно установить, поворачивая колесо до тех пор, пока зубец, представляющий эту цифру, не встанет против указателя или окошка. Например, три колеса показывают число 285. Мы можем прибавить к этому числу 111, повернув каждое колесо вправо на один зубец. Тогда против окошек встанут соответственно цифры 3, 9, 6, образуя сумму чисел 285 и 111, т. е. 396. Задача теперь в том, как осуществить перенос десятков. Это одна из основных проблем, которую пришлось решать Паскалю. Наличие такого механизма позволило бы вычислителю не тратить внимание на запоминание переноса из младшего разряда в старший. Машина, в которой сложение выполняется механически, должна сама определять, когда нужно производить перенос. Допустим, что мы ввели в разряд девять единиц. Счетное колесо повернется на 9/10 оборота. Если теперь прибавить еще одну единицу, колесо "накопит" уже десять единиц. Их надо передать в следующий разряд. Это и есть передача десятков.

В машине Паскаля ее осуществляет удлиненный зуб. Он сцепляется с колесом десятков и поворачивает его на 1/10 оборота. В окошке счетчика десятков появится единица - один десяток, а в окошке счетчика единиц снова покажется нуль. Механизм переноса действует только в одном направлении вращения колес и не допускает выполнения операции вычитания вращением колес в обратную сторону.

Поэтому Паскаль заменил операцию вычитания операцией сложения с десятичным дополнением. Пусть, например, необходимо из числа 285 вычесть 11. Метод дополнения приводит к действиям: 285-11=285-(100-89)=285+89-100=274. Нужно только не забывать вычесть 100. Но на машине, имеющей определенное число разрядов, об этом можно не заботиться. Вот как будет выполняться эта операция в шестиразрядной машине: 000285+999989=1000274; при этом единица слева выпадает, так как переносу из шестого разряда некуда деться.

Машина Паскаля была практически первым суммирующим механизмом, построенным на совершенно новом принципе, при котором считают колеса. Она производила на современников огромное впечатление, о ней слагались легенды, ей посвящались поэмы. Все чаще с именем Паскаля появлялась характеристика «французский Архимед». До нашего времени дошло только 8 машин Паскаля, из которых одна является 10-разрядной.

Универсальная автоматическая машина, в структуру которой уже входили почти все основные части современных ЭВМ, была изобретена еще в тридцатых годах XIX века. И сейчас мы можем лишь поражаться, что такая гигантская работа, - а это был, без преувеличений, переворот в вычислительной технике - могла быть совершена практически одним человеком.

Имя этого человека, которому суждено было открыть новую и, пожалуй, наиболее яркую страницу в истории вычислительной техники - Чарльз Бэббидж. За свою долгую жизнь (1792-1871) кембриджский профессор математики сделал немало открытий и изобретений, значительно опередивших его время.

Круг интересов Бэббиджа был чрезвычайно широк, и все же главным делом его жизни, по словам самого ученого, были вычислительные машины, над созданием которых он работал около 50 лет. Аналитическая машина Бэббиджа представляла собой единый комплекс специализированных блоков. По проекту она включала следующие устройства.

Первое - устройство для хранения исходных данных и промежуточных результатов. Бэббидж назвал его «складом»; в современных вычислительных машинах устройство такого типа называется памятью или запоминающим устройством. Для хранения чисел Бэббидж предложил использовать набор десятичных счетных колес. Каждое из колес могло останавливаться в одном из десяти положений и таким образом запоминать один десятичный знак. Колеса собирались в регистры для хранения многоразрядных десятичных чисел.

По замыслу автора запоминающее устройство должно было иметь емкость в 1000 чисел по 50 десятичных знаков «для того, чтобы иметь некоторый запас по отношению к наибольшему числу, которое может потребоваться».  Для сравнения скажем, что запоминающее устройство одной из первых ЭВМ имело объем 250 десятиразрядных чисел.

Для создания памяти, где хранилась информация, Бэббидж использовал не только колесные регистры, но и большие металлические диски с отверстиями. В памяти на дисках хранились таблицы значений специальных функций, которые использовались в процессе вычислений.

Второе устройство машины - устройство, в котором осуществлялись необходимые операции над числами, взятыми из «склада». Бэббидж назвал его «фабрикой», а сейчас подобное устройство называется арифметическим. Время на производство арифметических операций оценивалось автором: сложение и вычитание - 1с; умножение 50-разрядных чисел - 1 мин; деление 100-разрядного числа на 50-разрядное - 1 мин.

И наконец, третье устройство машины - устройство, управляющее последовательностью операций, выполняемых над числами. Бэббидж назвал его «конторой»; сейчас оно - устройство управления.

Управление вычислительным процессом должно было осуществляться с помощью перфокарт - набором картонных карточек с разным расположением пробитых (перфорированных) отверстий. Карты проходили под щупами, а они, в свою очередь, попадая в отверстия, приводили в движение механизмы, с помощью которых числа передавались со «склада» на «фабрику». Результат машина отправляла обратно на «склад». С помощью перфокарт предполагалось также осуществлять операции ввода числовой информации и вывода полученных результатов. По сути дела, этим решалась проблема создания автоматической вычислительной машины с программным управлением.

Только после смерти Бэббиджа его сын Генри сумел построить по чертежам отца центральный узел «Аналитической машины» (Приложение Рис. 9) - арифметическое устройство, которое в 1888 году вычислило произведения числа «пи» на числа натурального ряда от одного до 32 с точностью до 29 знаков! Машина Бэббиджа оказалась работоспособной, но Чарльз этого уже не увидел.

А машина, созданная Лейбницем в 1694 г., давала возможность механического выполнения операции умножения без последовательного сложения и вычитания. Главной частью ее был так называемый ступенчатый валик - цилиндр с зубцами разной длины, которые взаимодействовали со счетным колесом. Передвигая колесо вдоль валика, можно было его ввести в зацепление с необходимым числом зубцов и обеспечить установку определенной цифры. Арифметическая машина Лейбница была по существу первым в мире арифмометром – машиной (Приложение Рис. 10), предназначенной для выполнения четырех арифметических действий, позволяющей использовать 8-разрядное множимое и 9-разрядный множитель с получением 16-разрядного произведения.

По сравнению с машиной Паскаля было создано принципиально новое вычислительное устройство, существенно ускоряющее выполнение операций умножения и деления.

Однако, несмотря на все остроумие его изобретателя, арифмометр Лейбница не получил распространения по двум основным причинам: отсутствие на него устойчивого спроса и конструкционной неточности, сказывающейся при перемножении предельных для него чисел.

Но основная идея Лейбница - идея ступенчатого валика оказалась весьма плодотворной. Вплоть до конца XIX века конструкция валика совершенствовалась и развивалась различными изобретателями механических машин.

 

3. Электромеханический этап развития вычислительной техники

 

 

Как ни блестящ был век механических арифмометров, но и он исчерпал свои возможности. Людям нужны были более энергичные помощники. Это заставило изобретателей искать пути совершенствования вычислительной техники, но уже не на механической, а на электромеханической основе. Небольшой моторчик освободил вычислителя от необходимости крутить ручку, да и скорость счета увеличилась. Сам механизм счетного устройства, поначалу остававшийся неизменным, стал также постепенно модернизироваться.

Рычажный набор, который осуществлял медленную установку чисел и приводил к значительному проценту ошибок, заменили более удобным - клавишным. Появились машины, записывающие результат на бумажной ленте, а также другие комбинации счетных и пишущих устройств.

Это был уже новый шаг - механизация вычислений, но не их автоматизация. Управление процессом счета все еще ложилось на плечи человека. Классическим типом средств электромеханического этапа был счетно-аналитический комплекс, предназначенный для обработки информации на перфокарточных носителях.

Также была предложена Аланом Тьюрингом в 1936 году для формализации понятия алгоритма машина Тьюринга. Машина Тьюринга (Приложение Рис. 11) является расширением конечного автомата и способна имитировать все другие исполнители (с помощью задания правил перехода), каким-либо образом реализующие процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.

Машина Тьюринга имеет бесконечную в обе стороны ленту, разделенную на квадратики (ячейки). В каждой ячейке может быть записан некоторый символ из фиксированного (для данной машины) конечного множества, называемого алфавитом данной машины. Один из символов алфавита выделен и называется «пробелом», предполагается, что изначально вся лента пуста, то есть, заполнена пробелами.

Машина Тьюринга может менять содержимое ленты с помощью специальной читающей и пишущей головки, которая движется вдоль ленты. В каждый момент головка находится в одной из ячеек.

Машина Тьюринга получает от головки информацию о том, какой символ та видит, и в зависимости от этого (и от своего внутреннего состояния) решает, что делать, то есть какой символ записать в текущей ячейке и куда сдвинуться после этого (налево, направо или остаться на месте). При этом также меняется внутреннее состояние машины (мы предполагаем, что машина не считая ленты имеет конечную память, то есть конечное число внутренних состояний).

Так Тьюринг показал, что не существует «чудесной машины», способной решать все математические задачи. Но, продемонстрировав ограниченность возможностей, он на бумаге построил то, что позволяет решать очень многое и что мы теперь называем словом «компьютер».

Наконец, на электромеханическом этапе была реализована идея Бэббиджа создания универсальной вычислительной машины с программным управлением, по сложности соизмеримая с наиболее сложными техническими системами того времени. Уже на этом этапе выявляется зависимость возможностей вычислительной техники от ее системной сложности; многие наработки данного этапа легли в основу развития современного этапа развития ВТ - электронного.

 

4. Этап электронно-вычислительных машин

 

 

По этапам создания и используемой элементной базе ЭВМ условно делятся на поколения:

Первое поколение, 50-е годы. ЭВМ на электронных вакуумных лампах (Приложение Рис. 12).

Второе поколение, 60-е годы. ЭВМ на дискретных полупроводниковых приборах (транзисторах) (Приложение Рис. 13).

Третье поколение, 70-е годы. ЭВМ на полупроводниковых интегральных схемах с малой и средней степенью интеграции (сотни - тысячи транзисторов в одном корпусе) (Приложение Рис. 14).

Четвертое поколение, 80-е годы. ЭВМ на больших и сверхбольших интегральных схемах - микропроцессорах (десятки тысяч - миллионы транзисторов в одном) (Приложение Рис. 15).

Пятое поколение, 90-е годы. ЭВМ с многими десятками параллельно работающих микропроцессоров, позволяющих строить эффективные системы обработки знаний; ЭВМ на сверхсложных микропроцессорах с параллельно-векторной структурой, одновременно выполняющих десятки последовательных команд программы (Приложение Рис. 16).

Шестое поколение, оптоэлектронные ЭВМ с массовым параллелизмом и нейтронной структурой - с распределенной сетью большого числа (десятки тысяч) несложных микропроцессоров, моделирующих архитектуру нейтронных биологических систем (Приложение Рис. 17).

Каждое следующее поколение ЭВМ имеет по сравнению с предыдущими существенно лучшие характеристики.

 

 

 

 

5. Суперкомпьютеры

 

 

Первые суперкомпьютеры появились уже среди компьютеров второго поколения, они были предназначены для решения сложных задач, требовавших высокой скорости вычислений.

Это LARC фирмы UNIVAC, Stretch фирмы IBM и "CDC-6600"(семейство CYBER) фирмы Control Data Corporation, в них были применены методы параллельной обработки (увеличивающие число операций, выполняемых в единицу времени), конвейеризация команд (когда во время выполнения одной команды вторая считывается из памяти и готовится к выполнению) и параллельная обработка при помощи процессора сложной структуры, состоящего из матрицы процессоров обработки данных и специального управляющего процессора, который распределяет задачи и управляет потоком данных в системе.

Компьютеры, выполняющие параллельно несколько программ при помощи нескольких микропроцессоров, получили название мультипроцессорных систем. Отличительной особенностью суперкомпьютеров являлись векторные процессоры, оснащенные аппаратурой для параллельного выполнения операций с многомерными цифровыми объектами - векторами и матрицами. В них были встроены векторные регистры и параллельный конвейерный механизм обработки. Если на обычном процессоре программист выполнял операции над каждым компонентом вектора по очереди, то на векторном - выдавал сразу векторые команды.

Компьютеры фирмы Cray Research были классикой в области векторноконвейерных суперкомпьютеров. Существует легенда, что первый суперкомпьютер Cray был собран в гараже, однако этот гараж был размером 20 х 20 метров, а платы для нового компьютера заказывались на лучших заводах США. В 1964 году был создан компьютер CDC6600, а в 1969 году - CDC7600, вошедшие в семейство CYBER.

Для повышения быстродействия в суперкомпьютерах семейства CYBER использовались методы конвейерной и параллельной обработки при помощи процессора сложной структуры, состоящего из матрицы процессоров обработки данных и специального управляющего процессора, который распределял задачи и управлял потоком данных в системе. В 1972 году был создан сверхпроизводительный компьютер ILIAC4 (США) с конвейерной архитектурой, включавшей 64 процессора.

Это был наиболее крупный проект среди компьютеров третьего поколения. Разрабатывали компьютер сотрудники Илинойского университета во главе с Д. Слотником. Компьютер был предназначен для решения системы уравнений в частных производных при помощи итерационных разностных схем. Решение такой задачи могло быть ускорено в 64 раза по сравнению с последовательным вычислением на однопроцессорном компьютере.

Максимальное быстродействие компьютера составляло 200Млн.операций в секунду. Приведем параметры суперкомпьютера CONVEX C-3440. Суперкомпьютер включал в себя 4 векторных процессора, 1 процессор ввода-вывода, объем физической памяти составлял 512 Мб, объем виртуальной памяти до 4 Гб, объем памяти на жестких дисках 4,5 Гб, 9-дорожечный накопитель на магнитной ленте, интерфейс Ethernet (10 Мбит/сек), 16-канальный мультиплексор. Пиковая производительность суперкомпьютера составляла 800 Мфлоп/сек.

 В 1989 году была пущена в опытную эксплуатацию векторноконвейерная супер ЭВМ Электроника ССБИС разработки Института проблем кибернетики РАН и предприятий электронной промышленности. Производительность в однопроцессорном варианте составляла 250 MFLOPS, передача данных между массовой интегральной памятью и оперативной памятью осуществлялась под управлением специализированного процессора, реализующего произвольные методы доступа. Разработку супер-ЭВМ вели В.А. Мельников, Ю.И. Митропольский, В.З. Шнитман, В.П. Иванников.

В 1990 году в Советском Союзе была введена в эксплуатацию векторно-конвейерная супер-ЭВМ "Эльбрус 3.1" на базе модульных конвейерных прцессоров (МКП), разработанная в ИТМ и ВТ имени С.А. Лебедева группой конструкторов, в которую входили Г.Г. Рябов, А.А. Соколов, А.Ю. Бяков. Производительность суперкомпьютера в однопроцессорном варианте составляла 400 MFLOPS. В 1996 году японская компания Fujitsu пополнила класс суперкомпьютеров новой машиной VPP700, позволяющей подключать до 256 рабочих мест, имеющую производительность 500 миллиардов операций с плавающей точкой в секунду. Этот векторный компьютер был предназначен для научных и технических расчетов. Размер дисковой памяти мог варьироваться от 4 до 512 Гбайт.

Фирмой IBM был разработан суперкомпьютер Deep Blue, как система массового параллелизма. Это, был первый компьютер, победивший чемпиона мира по шахматам. Компьютер Deep Blue разрабатывался первоначально в университете Carnegie Mellon студентами Фенг-хсиунгом Хсу и Марри Кампбеллом на чипсете, использовавшемся в компьютере Sun 3/160. Проект был принят к исполнению фирмой IBM в 1989, когда Кампбелл пришел работать в фирму. В этом году впервые против чемпиона мира Гарри Каспарова играл компьютер Deep Though.

Каспаров легко обыграл компьютер в двух партиях. Следующее состязание Каспарова состоялось в феврале 1996 с компьютером Deep Blue. Компьютер был собран на 32-х восьмипроцессорных кластерах RS/6000. Каспаров выиграл снова. К февралю 1997 года была разработана новая шахматная программа и значительно увеличена скорость вычислений компьютера, и тогда "Голубому гиганту" удалось победить Каспарова со счетом 3.5:2.5. В 1997 году 16 из 20 самых быстpых суперкомпьютеров были произведены в Соединенных Штатах, 4 - в Японии. Ни один из суперкомпьютеров, которые были введены в строй в 1997 году, не был создан в европейской стране.

Российский Институт Высокопроизводительных Вычислений и Баз Данных является одним из крупнейших суперкомпьютерных центров в Восточной Европе.

В апреле 1998 года проект компьютера класса Beowulf "Паритет" был одобрен Министерством Науки и Технологий РФ. "Паритет" включал в себя 4 узла, состоящих из 2x процессоров Intel Pentium II (450МГц), жесткого диска емкостью 9,1 Гбайт, быстрой памяти RAM (512 Мб). Суперкомпьютеры 21 века.

В 2008 пиковая производительность суперкомпьютера Jaguar, установленного в лаборатории министерства энергетики США, составляла 1,64 петафлоп, сообщает InformationWeek. Ранее самым мощным считался суперкомпьютер IBM Roadrunner, с производительностью 1,026 петафлоп. В основе суперкомпьютера лежало 45 тысяч процессоров AMD Opteron и 362 терабайта оперативной памяти. Ученые использовали ( и используют) Jaguar, например, для моделирования климатических изменений.

Также суперкомпьютер задействован в такой области, как возобновляемые источники энергии.

До начала 2009 Jaguar находился в стадии тестирования. Он был использован для проведения тестовых расчетов, которые требуют производительность свыше 1,3 петафлоп.

2010 год. Китайская система Tianhe-1A официально возглавила рейтинг 500 мощнейших суперкомпьютеров мира. Tianhe-1A- суперкомпьютер , установивший рекорд производительности в 2,507 петафлоп в бенчмарке LINPACK, став самой быстрой системой в Китае и во всем мире. В основе Tianhe-1A лежат современные гетерогенные вычисления на основе параллельной работы графических процессоров и многоядерных центральных процессоров , которые обеспечили значительный прирост в производительности и позволили уменьшить размеры системы и сократить энергопотребление. Система построена на 7168 графических процессорах NVIDIA Tesla M2050 и 14336 CPU; идентичную производительность можно достичь только при использовании более 50 000 CPU на гораздо большей площади. Более того, система в 2,507 петафлопс, построенная исключительно на CPU, потребляла бы свыше 12 мегаватт.

Благодаря графическим процессорам и гетерогенной среде вычислений, Tianhe-1A потребляет всего 4,04 мегаватта, т.е. в три раза меньше - такая разница в энергопотреблении достаточна для подачи электричества в более чем 5000 домов в течение года.

 Универсальный персональный суперкомпьютер с Linux. В рамках президентской программы «Развитие суперкомпьютеров и ГРИД-технологий» федеральный ядерный центр в Сарове (РФЯЦ-ВНИИЭФ), входящий в госкорпорацию «Росатом», разработал две модели персональных суперкомпьютеров - универсального и специального назначения, а также программные пакеты для математического моделирования, работающие под управлением ОС Linux.

На протяжении 2011 года атомщики расширяют ассортимент и значительно увеличивают поставки таких систем. Универсальный суперкомпьютер (Приложение Рис. 18) предназначен для широкого спектра инженерных расчетов и может устанавливаться непосредственно на рабочем месте сотрудника.

 Его пиковая производительность составляет 1 Тфлопс. Он построен на базе двенадцатиядерных процессоров AMD и включает три четырехсокетные материнских платы. Всего система содержит 144 процессорных ядра.

 

 

 

Заключение

 

 

Как мы можем наблюдать, развитие в сфере вычислительной технике не останавливается ни на секунду. После удешевления комплектующих к компьютеру и их минимизации в конце XX века, сами персональные компьютеры стали стоить в разы дешевле. Благодаря этому теперь многие граждане, проживающие в развитых странах, могут позволить себе собственный персональный компьютер. После такого события, количество пользователей персональных компьютеров начало стремительно расти вверх, тем самым повышая спрос на создание улучшенной продукции данного типа. Технический прогресс не стоит на месте. В этом можно убедиться, если сравнить первые телевизоры, холодильники, мобильные телефоны, компьютеры с современными моделями. Увеличилась также доступность бытовых приборов. 30 лет назад в магазинах записывались на очередь, чтобы купить холодильник, телевизор или автомобиль, компьютеры видели только в кино, а о посудомоечной машине даже мечтать не могли.

Из этого всего стоит сделать вывод, что данный прогресс в вычислительной технике будет оставаться прежним ещё множество десятков а то и сотен лет. Сейчас в каждом городе есть несколько магазинов по продаже компьютеров и другой бытовой техники, поэтому каждый человек имеет возможность купить себе компьютер, исходя из цены, качества и необходимых функций.

 

Список литературы

 

 

1.                 Владимиров В. Развитие вычислительной техники // Домашний лицей. – 2003 – N 1 - С. 46-57.

2.                 Гаков В. Ископаемые вычислительные // Коммерсантъ Деньги. – 2001 - N 1/2. - С. 41-45.

3.                 Дубровский А. Чтим прошлое, работаем на будущее. К 60-летию отечественной вычислительной техники // Наука и жизнь. - 2008 - N 6 - С. 60-61.

4.                 Зубов Ю. И. История создания цифровых электронных вычислительных машин // История науки и техники. – 2002 - N 1 - С. 2-11.

5.                 Зубрилин А. А. Факультативные занятия по теме "История развития вычислительной техники" // Информатика и образование. – 2006 - N 4 - С. 2-12.

6.                 Зубрилин А. А. Факультативные занятия по теме "История развития вычислительной техники" // Информатика и образование. – 2006 - N 6 - С. 27-35.

7.                 Ицкович Э. Л. История развития отечественных вычислительных средств автоматизации // Промышленные АСУ и контроллеры. – 2007 - N 6 - С. 57-60.

8.                 https://ru.wikipedia.org

9.                 http://csaa.ru

10.            https://www.polnaja-jenciklopedija.ru

 

 

Приложение

 

Рис. 1 Пальцевый счет

 

Рис. 2 Абак

Рис. 3 Калькулятор

Рис.4 Счеты

Рис.5 Арифмометр

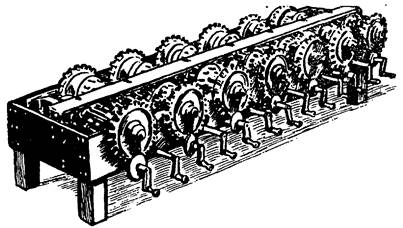
Рис. 6 13-разрядное суммирующие устройство Леанардо да Винчи

 

 

 

Рис. 7 Машина Шиккарда

 

Рис. 8 Паскалина

 

Рис. 9 Аналитическая машина Чарльза Бэббиджа

Рис. 10 Арифмометр Лейбница

Рис. 11 Машина Тьюринга

Рис. 12 ЭВМ первого поколения

 

 

Рис. 13 ЭВМ второго поколения

Рис. 14 ЭВМ третьего поколения

Рис. 15 ЭВМ четвертого поколения

Рис. 16 ЭВМ пятого  поколения

Рис. 17 ЭВМ шестого поколения

Рис. 18 Суперкомпьютер

 

Скачано с www.znanio.ru