Муниципальное бюджетное общеобразовательное учреждение

Средняя общеобразовательная школа № 13 городского округа Вичуга

 

 

 

 

 

 

 

Индивидуальный итоговый проект по математике

«Способы решения финансовых задач ЕГЭ»

 

 

 

 

 

 

 

Автор проекта:

Мурашова Анастасия Витальевна

Ученица 10 класса

Руководитель:

Смирнова Тамара Александровна

Вичуга

2023

 

Содержание

 

Введение. 2

1. Основная часть. 3

  1.1 Проценты в математике. 3

  1.2 Прогрессия. 5

  1.3 Финансовая математика. 6

  1.4 Типы финансовых задач. 10

2. Практическая часть. 12

Заключение. 22

Список литературы. 23

Приложение. 24

 

 

 

 

 

 

 

 

 

 

 

 

 

Введение

·        Актуальность

Актуальность данной темы обусловлена тем, что спектр данных финансовых задач представлен в ЕГЭ, а в школьной программе проценты проходятся в средней школе и могут забыться. Кроме того в рамках выполнения проекта был проведен опрос среди учащихся 10 и 11 классов (Приложение 1,2), который выявил то, что многие из респондентов не умеют решать экономические задачи. Также в современном мире необходимо разбираться в потоке информации связанной с финансами. Уметь определять выгодно ли предложение банка для кредитов и будущих накоплений так как практический каждый на протяжении своей жизни сталкивается либо с кредитом, либо с накоплениями и от того насколько грамотно люди подходят к данному вопросу зависит конечный результат.

·        Проблема

Отсутствие знаний в области финансовой математики влияет не только на результаты ЕГЭ и понижает шансы на максимальный балл за экзамен, но и на финансовую грамотность необходимую для успешной деятельности в дальнейшей жизни.

·        Гипотеза

Умеют ли ребята нашей школы решать экономические задачи?

·        Цель

Создать справочник для решения экономических задач.

·        Задачи:

1) Изучить теоретический материал по данной теме;    

2) Систематизировать виды экономических заданий, включенных во вторую часть ЕГЭ по математике профильного уровня, и методы решения этих задач.

·        Объект и предмет исследования

Объект: финансовые задачи Единого Государственного Экзамена.

Предмет исследования: способы решения финансовых задач ЕГЭ.

·        Методы исследования

Теоретический анализ и обобщение научной и учебной литературы по данной теме, сравнение, систематизация информации, выводы, подбор и решение задач, опрос.

 

 

 

 

 

 

 

 

1. Основная часть

 

1.1 Проценты в математике

Определение процента

 

Одним из фундаментальных понятий математики является процент. Чтобы понять, что такое процент, достаточно разделить данное целое число на сто. Таким образом, получает, что процент – это одна сотая часть. Обозначающим знаком является %.

Чтобы перевести проценты в десятичную дробь, нужно убрать знак % и разделить известное на 100. Например, 21% — это 21: 100 = 0,21. А если нужно перевести натуральное число или десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например, 0,21 = 0,21 · 100% = 21%.

Нахождение процентов от числа

1 способ
1	Найдем, чему равен 1%
2	Умножим полученное значение на количество искомых процентов

 

 

 

Пример: найти 15% от 45.

1)

2)

 

 

2 способ
1	Переведем проценты в десятичную дробь
2	Умножим число на полученную десятичную дробь

 

 

Пример: найти 15% от 45.

1)

2)

Нахождение числа по его проценту

Чтобы найти число по его проценту, нужно его известную часть разделить на то, сколько процентов она составляет от числа.

Например: Саша решила 30 задач из учебника. Что составляет 15% числа всех задач в книге. Сколько всего задач собрано в этом учебнике?

1)

2) .

2.2 Прогрессия

 

Арифметическая прогрессия

Арифметическая прогрессия – это последовательность, в которой каждый следующий член можно найти, прибавив к предыдущему одно и то же число d. Для любого натурального значения n справедлива зависимость:

,

 где d – разность арифметической прогрессии.

Формула n-го члена арифметической прогрессии:

,

где n – порядковый номер члена прогрессии;

a₁ – первый член прогрессии;

d – разность.

Арифметическая прогрессия бывает трех видов:

1)Возрастающая — арифметическая прогрессия, у которой положительная разность, то есть .

2)Убывающая — арифметическая прогрессия, у которой отрицательная разность, то есть .

3)Стационарная — арифметическая прогрессия, у которой разность равна нулю, то есть .

Сумма первых n членов арифметической прогрессии () обозначается:

Формулы нахождения суммы n членов арифметической прогрессии:

 

Геометрическая прогрессия

Геометрическая прогрессия – это последовательность, в которой каждый член, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.

Любой член геометрической прогрессии вычисляет по формуле:

,

где n – порядковый номер члена прогрессии;

b₁ – первый член прогрессии;

q – знаменатель.

Формула суммы первых n членов геометрической прогрессии:

,

где b₁ – первый член геометрической прогрессии;

b_n – n-ый член геометрической прогрессии;

q – знаменатель;

n – количество членов последовательности.

 

 

 

2.3 Финансовая математика

 

Понятие финансовой математики

Финансовая математика - раздел прикладной математики, имеющий дело с математическими задачами, связанными с финансовыми расчётами.

Основные понятия финансовой математики

Основные понятия финансовой математики относятся к процентам, процентным ставкам и методам их расчета. Итак, к основным понятиям можно отнести:

·       Проценты – это доход, полученный от предоставления капитала в долг в различных формах (ссуды, займы и т.д.), либо от производственных или финансовых вложений.

·       Процентная ставка – это величина, характеризующая интенсивность начисления процентов.

·       Наращение (увеличение) первоначальной суммы долга – это увеличение суммы долга за счет добавления начисленных процентов (дохода).

·       Множитель (коэффициент) наращения – это величина, которая показывает, во сколько раз увеличился первоначальный капитал.

·       Период начисления – это период, за который начисляются проценты (получен доход). Период начисления можно разделить на расчетные интервалы.

·       Интервал начисления - это минимальный период, по истечении которого начисляются проценты.

Размер полученного дохода (т. е. процентов) определяется на основе суммы инвестированного капитала, периода, на который он был заимствован или инвестирован, размера и типа процентной ставки (доходности).  Существуют два способа определения и начисления процентов, приведенные в таблице 1.

Таблица 1 - Два способа определения и начисления процентов

1	Декурсивный	Проценты начисляются в конце каждого расчетного интервала. Их величина определяется на основе предоставленного капитала. Декурсивная процентная ставка (проценты по ссуде) - это процент от суммы дохода, начисляемой в течение определенного интервала, к сумме, доступной в начале этого интервала.
2	Антисипативный	Проценты начисляются в начале каждого расчетного интервала. Размер процентных платежей определяется исходя из наращенной суммы. Антисипативный процент (учетная ставка) - это процент от суммы дохода, выплачиваемой за определенный интервал, к сумме наращенной суммы, полученной после этого интервала.

 

В обоих случаях начисления процентов процентные ставки могут быть:

1)Простыми – когда они применяются к одной и той же начальной сумме в течение всего расчетного периода;

2)Сложными – когда они применяются к сумме долга и процентам в предыдущих расчетных интервалах после каждого расчетного интервала.

Понятия аннуитетных, фиксированных и дифференцируемых платежей

Аннуитетный платеж – это платеж, при котором общая сумма ежемесячных платежей остается неизменной до конца срока кредита. Месячный аннуитетный платеж находится по формуле:

,

где X – месячный платеж;

S – первоначальная сумма кредита;

P – 1/12 процентной ставки;

N – количество месяцев.

Фиксированные платежи - это платежи, которые четко определены в условиях задачи.

Дифференцируемый платеж – это платеж, при котором на этом первом этапе ссуда выплачивается крупными суммами, но ежемесячные взносы постепенно уменьшаются.

Формула для расчета дифференцированного платежа состоит из нескольких частей:

,

где P – размер дифференцированного платежа по кредиту;

St – сумма платежа по основному долгу;

In – сумма платежа по начисленным на остаток процентам.

Расчет суммы платежа по основному долгу:

,

где St – сумма платежа по основному долгу;

S – сумма кредита;

n – количество месяцев, в течение которых выплачивается кредит.

Расчет доли процентов:

,

где In – сумма платежа по начисленным на остаток процентам;

Sn – остаток задолженности по кредиту;

i – годовая процентная ставка;

d – количество дней в расчетном месяце;

D – количество дней в году.

2.4 Типы финансовых задач

Условно финансовые задачи делятся на несколько типов. Это кредиты, вклады и задачи на оптимальный выбор. Задачи связанные с кредитами делятся на 6 подтипов.

Кредиты

1) Вычисление процентной ставки по кредиту;

2) Нахождение количества лет (месяцев) выплаты кредита;

3) Нахождение ежегодного (ежемесячного) перевода;

4) Нахождение суммы кредита;

5) Нахождение разницы (аннуитетные платежи);

6) Задачи с таблицей в условии;

 

3. Практическая часть

3.1 Способы решения всех типов

Кредит

1 подтип: Вычисление процентной ставки по кредиту.

Пример №1:

В июле 2016 года планируется взять кредит в размере 4,2 млн. руб. Условия возврата таковы: 

— каждый январь долг возрастает на r% по сравнению с концом предыдущего года. 

— с февраля по июнь необходимо выплатить часть долга.

— в июле 2017, 2018 и 2019 годов долг остается равным 4,2 млн. руб. 

— суммы выплат 2020 и 2021 годов равны.

Найдите r, если в 2021 году долг будет выплачен полностью и общие выплаты составят 6,1  млн. рублей.

Решение:

Ежегодно вклад увеличивается в b раз, где .

В первые три года платежи будут равны x млн. рублей, ведь остаток долга остается равным 4,2 млн. руб. В последние два года платежи будут равны y млн. рублей.

Для наглядности составим таблицу:

Год	Долг	Платеж	Остаток долга
2017
2018
2019
2020
2021

 

Составим уравнение исходя из расчетов 2017 года:

;

Выразим x через b:

                                               .                                         (1)

Остаток долга в 2021 году будет равен 0:

;

Выразим y через b:

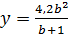                                      , где b+1 ≠ 0.                                        (2)

Сумма всех платежей составила:

.                                                 (3)

Поставим в уравнение (3) значения x (1) и y (2):

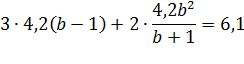
Решим полученное уравнение:

;

;

;

;

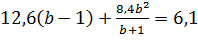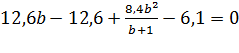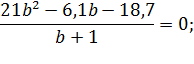
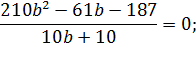
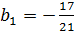 ( этот корень не подходит, так как процентная ставка не может быть отрицательным числом);

.

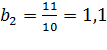Так как: , то ;

Из этого равенства r = 10.

Ответ: 10.

2 подтип: Нахождение количества лет (месяцев) выплаты кредита.

Пример №2:

1 января 2015 года Павел Витальевич взял в банке 1 млн рублей в кредит. Схема выплаты кредита следующая: 1 числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Павел Витальевич переводит в банк платёж. На какое минимальное количество месяцев Павел Витальевич может взять кредит, чтобы ежемесячные выплаты были не более 125 тыс. рублей?

Решение:

Найдем минимальное количество месяцев, в течение которых Павел может погасить основную сумму долга, если его ежемесячный платеж будет составлять 125 тысяч рублей: 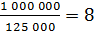(месяцев).

Но банк начисляет 1% от оставшейся суммы долга ежемесячно. Таким образом, мы получаем, что общая сумма задолженности превышает 1 миллион рублей.

Составим таблицу, которая наглядно иллюстрирует схему кредитования, и найдем № месяц, в котором задолженность меньше ежемесячного платежа:

Месяц, №	Долг в начале месяца, руб.	Долг после выплаты, руб.
1
2
3
4
5
6
7
8
9

 

Ответ: 9 месяцев.

 

3 подтип: Нахождение ежегодного (ежемесячного) перевода.

Пример №3:

31 декабря 2014 года Алексей взял в банке 6 902 000 рублей в кредит под 12,5% годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Алексей переводит в банк X рублей. Какой должна быть сумма X, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за четыре года)?

Решение:

S – сумма кредита;

p – процентная ставка;

X – сумма выплат.

Каждый год сумма долга увеличивается на 12,5%

Год	Долг, руб.	Платеж, руб.	Остаток, руб.
1
2
3
4

 

За 4 года Алексей должен погасить кредит, следовательно:

.

;

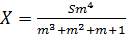; где .

Величина m при процентной ставке 12,5 равна:

.

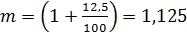Найдем сумму выплат:

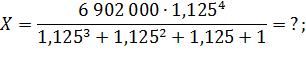
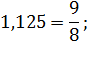
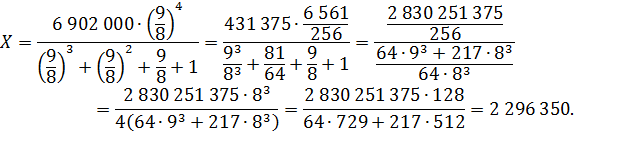
Ответ: 2 296 350.

4 подтип: Нахождение суммы кредита.

Пример №4:

Планируется выдать льготный кредит на целое число миллионов рублей на пять лет. В середине каждого года действия кредита долг заёмщика возрастает на 20 % по сравнению с началом года. В конце 1-го, 2-го и 3-го годов заёмщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 4-го и 5-го годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наименьший размер кредита, при котором общая сумма выплат заёмщика превысит 10 млн.

Решение:

S – полная сумма кредита;

X – платеж в конце 4-го и 5-го годов

Составим таблицу погашения:

 

Дата	Долг, млн. руб.	Платеж, млн. руб.	Остаток, млн. руб.
1
2
3
4
5

 

Решаем уравнение:

.

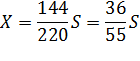
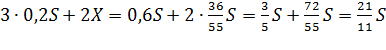По условию общая сумма выплат превысит 10 млн. рублей:

;

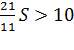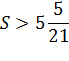
Ответ: 6 млн. рублей.

5 подтип: Нахождение разницы (аннуитетные платежи)

Пример №5:

31 декабря 2014 года Савелий взял в банке 7 378 000 рублей в кредит под 12,5% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Савелий Переводит в банк платёж. Весь долг Савелий выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа?

Решение:

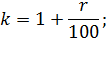
Найдем коэффициент:

 

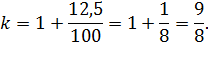
Если Савелий будет выплачивать долг тремя равными платежами X, то мы получим:

Из полученного уравнения выразим X:

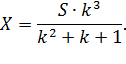
Всего он выплатит .

Если Савелий будет выплачивать долг двумя равными платежами Y, то мы получим:

Из полученного уравнения выразим Y:

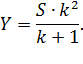
Всего он выплатит .

Тогда разница будет равна:

;

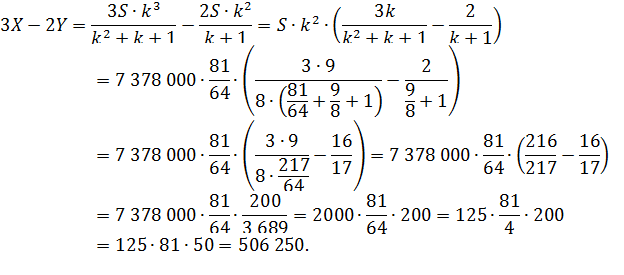
Ответ: 506 250.

6 подтип: Задачи с таблицей в условии.

Пример №6:

В июле 2022 года планируется взять кредит в банке на четыре года в размере S млн рублей, где S — целое число. Условия его возврата таковы:

— каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;

 — в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.

Месяц и год	Июль 2022	Июль 2023	Июль 2024	Июль 2025	Июль 2026
Долг, млн. руб.

 

Найдите наибольшее значение S, при котором каждая из выплат будет меньше 3 млн. рублей.

Решение:

Год	Долг	Выплата	Долг после выплаты
2023
2024
2025
2026

 

Решим систему:

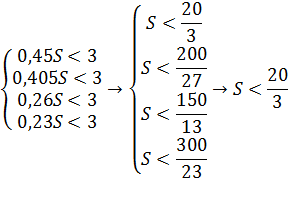
Ответ: 6.

Вклады

Пример №7:

В банк был положен вклад под 10% годовых. Через год, после начисления процентов, вкладчик снял со счета 2000 рублей, а еще через год (опять после начисления процентов) снова внес 2000 рублей. Вследствие этих действий через три года со времени открытия вклада вкладчик получил сумму меньше запланированной (если бы не было промежуточных операций со вкладом). На сколько рублей меньше запланированной суммы он получил?

Решение:

S – сумма вклада.

Начисление процентов по вкладу:

Год	Полученная сумма, руб.	Запланированная сумма, руб.
1
2
3

 

Ответ: 220.

Задачи на оптимальный выбор

Пример №8:

При оплате услуг через платежный терминал взимается комиссия 5%. Терминал принимает суммы, кратные 10 рублям. Аня хочет положить на счет

своего мобильного телефона не меньше 300 рублей. Какую минимальную сумму она должна положить в приемное устройство данного терминала?

Решение:

X рублей – минимальная сумма, подходящая под условие задачи. По условию задачи составим неравенство:

Найдем x:

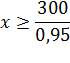
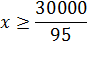
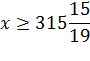
По условию задачи терминал приминает суммы, кратные 10 рублям, поэтому минимальная сумма составляет 320 рублей.

Ответ: 320 рублей.

Задачи для закрепления представлены в Приложении 3.

 

 

Заключение

Я считаю, что в ходе этого исследования достигла своей цели. Я изучила, какие виды финансовых заданий предлагаются на едином государственном экзамене, какие математические концепции необходимы для решения таких задач. Были рассмотрены основные методы решения задач с кредитами, вкладами и оптимальным выбором. Я научилась решать различные типы задач, выбирая лучший для меня метод (с помощью создания таблиц).

Способность решать такие задачи позволяет рассчитывать платежи по кредитам и прибыль по депозитам, а также применять эти знания в повседневной жизни. И, конечно же, получить более высокий балл на едином государственном экзамене.

Тема работы очень актуальна, так как все рассматриваемые задания взяты из материалов для подготовки к единому государственному экзамену по профильной математике.

 

 

Список литературы

 

1. Алгебра. 9 класс: Учеб. для общеобразовательных учеб. заведений / К.С. Муравин, Г.К. Муравин, Г.В. Дорофеев. - М.: Дрофа, 2009.

2. Интернет ресурс. Режим доступа: https://math-ege.sdamgia.ru/test?theme=292 ( Дата обращения 03.03.23).

3.  Прокофьев А.А., Корянов А.Г. Математика. ЕГЭ. Социально-экономические задачи: теория, задания, примеры решений. 10-11 классы. – Ростов-на-Дону, Легион, 2016. – 128 с.

4. Колесникова С.И. Экономические задачи ЕГЭ / С.И. Колесникова. – М.: ООО «Азбука-2000», 2016. – 32 с.

 

                                                  Приложение 1                         

В ходе опроса учащимся задавался вопрос «Знаете ли вы, что во второй части ЕГЭ по профильной математике присутствуют экономические задачи?»

 

Результаты опроса представлены в диаграмме 1

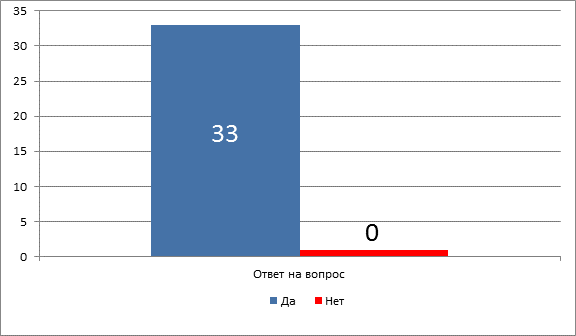
По результатам первого опроса можно сделать вывод, что старшеклассники знают о присутствии экономических задач в экзамене.

 

 

 

 

 

 

 

 

 

 

 

Приложение 2

Второй вопрос в исследовании звучал так: «Умеете ли вы решать экономические задачи?»

 

Результаты опроса представлены в диаграмме 2

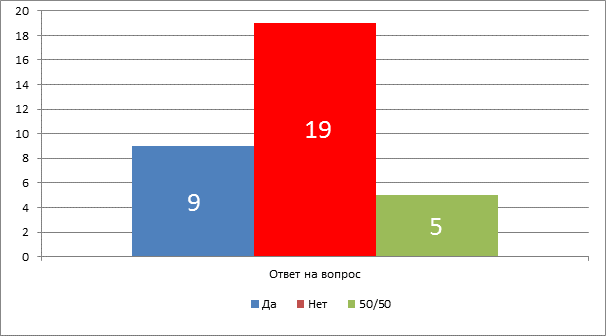
По результатам второго опроса можно сделать вывод, что большинство учащихся не умеют решать задачи экономического содержания.

 

 

 

 

 

 

 

 

 

 

 

Приложение 3

Задачи для закрепления

1) Жанна взяла в банке в кредит 1,2 млн. рублей на срок 24 месяца. По договору Жанна должна вносить в банк часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 2%, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна выплатит банку в течение первого года кредитования?

Ответ: 822 тыс. рублей.

2) В банк помещена сумма 3900 тысяч рублей под 50% годовых. В конце каждого из первых четырех лет хранения после начисления процентов вкладчик дополнительно вносил на счет одну и ту же фиксированную сумму. К концу пятого года после начисления процентов оказалось, что размер вклада увеличился по сравнению с первоначальным на 725%. Какую сумму вкладчик ежегодно добавлял к вкладу?

Ответ: 210 тыс. руб.

3) В 1-е классы поступает 43 человека: 23 мальчика и 20 девочек. Их распределили по двум классам: в одном должно получиться 22 человека, а в другом ― 21. После распределения посчитали процент мальчиков в каждом классе и полученные числа сложили. Каким должно быть распределение по классам, чтобы полученная сумма была наибольшей?

Ответ: В одном классе ― 21 мальчик, в другом ― 20 девочек и 2 мальчика.

 

 

Скачано с www.znanio.ru