информатика

Описание методической разработки урока

Тема урока: «Круги Эйлера»

Тип урока: интегрированный с математикой, урок объяснения нового материала, а также обобщения и систематизации знаний, умений и навыков.

Вид урока: урок теоретических и практических работ, анализ ситуации.

Методы обучения: диалогический, наглядный, объяснительно – иллюстративный.

Формы обучения: коллективная и индивидуальная.

Структура урока: орг. момент, актуализация опорных знаний, формирование новых понятий и способов действий, систематизация ЗУН, закрепление полученных навыков и умений, работа в команде, подготовка к восприятию Д/З, подведение итогов урока.

Оборудование: ПК, проектор, авторские презентации «Проверка Д/З», «Круги Эйлера. Теория», «Задачи на составления запросов поисковику», «Решение задач с помощью кругов Эйлера».

Цели урока:

·         обобщить знания и умения обучающихся по применению таблиц истинности при решении логических задач;

·         познакомить и сформировать у обучающихся принцип реализации диаграмм Вена-Эйлера для решения логических задач;

·         развить коммуникативно - технические умения, умения оценивать результаты выполненных действий;

·         развить аналитическо-логическое мышление;

·         воспитать самостоятельность, инициативность, толерантность, ответственное отношение к информации, информационную культуру.

Задачи урока:

·         повторить изученный материал по теме «Логика»;

·         научить обучающихся использовать круги Эйлера при решении логических задач;

·         продемонстрировать решение типовых задач из ГИА и ЕГЭ;

·         закрепить изученный материал решением подобных задач.

Круги Эйлера

Эйлеровы круги (круги Эйлера) — принятый в логике способ моделирования, наглядного изображения отношений между множествами с помощью кругов, предложенный знаменитым математиком Л. Эйлером (1707–1783). Он  говорил о названных его именем схемах: «круги подходят для того, чтобы облегчить наши размышления». Эйлер считается немецким, швейцарским и даже российским математиком, механиком и физиком. Дело в том, что он много лет проработал в Петербургской академии наук и внес существенный вклад в развитие российской науки.

До него подобным принципом при построении своих умозаключений руководствовался немецкий математик и философ Готфрид Лейбниц.

Метод Эйлера получил заслуженное признание и популярность. И после него немало ученых использовали его в своей работе, а также видоизменяли на свой лад. Например, чешский математик Бернард Больцано использовал тот же метод, но с прямоугольными схемами.

Свою лепту внес также немецкий математике Эрнест Шредер. Но главные заслуги принадлежат англичанину Джону Венну. Он был специалистом в логике и издал книгу «Символическая логика», в которой подробно изложил свой вариант метода (использовал преимущественно изображения пересечений множеств).

Обозначение отношений между объемами понятий посредством кругов было применено еще представителем афинской неоплатоновской школы — Филопоном (VI в.), написавшим комментарии на «Первую Аналитику» Аристотеля.

Диаграммы Эйлера своим наглядным графическим изображением не только облегчают запоминание структуры различных сочетаний мыслей, но и помогают решению ряда задач, стоящих перед формальной логикой.

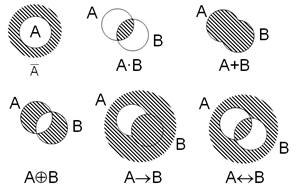
Для наглядной геометрической иллюстрации объемов понятий и соотношений между ними используется диаграммы Эйлера-Венна (круги Эйлера). Если имеются какие-либо понятия А, В, С и т.д., то объем каждого понятия (множество) можно представить в виде круга, а отношения между этими объектами (множествами) – в  виде пересекающихся кругов.

Заштрихованные области показывают результат логических операций подписанных снизу.

Описание хода урока