Информатика 9 класс Решение задач с применением кругов Эйлера

 Круги Эйлера

Задача (Простая)

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

 

Запрос	Найдено страниц (в тысячах)
Пушкин	3500
Лермонтов	2000
Пушкин | Лермонтов	4500

 

Какое количество страниц (в тысячах) будет найдено по запросу Пушкин & Лермонтов? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

Видим, что по запросу "Пушкин" в поисковике нашлось 3500 страниц. По запросу "Лермонтов" - 2000 страниц.

 

Запрос "Пушкин | Лермонтов" обозначает, что поисковик выдаст страницы, где есть слова про "Пушкина", и страницы, где есть слова про "Лермонтова", а так же могут быть страницы, где написано и про "Пушкина", и про "Лермонтова" одновременно.

 

Если сложить страницы, в которых написано про "Пушкина" и про "Лермонтова" получается 3500 + 2000 = 5500 страниц. Но почему же при запросе "Пушкин | Лермонтов" получается меньше страниц, всего 4500 ?

 

Этот факт обозначает то, что когда мы подсчитывали страницы про "Пушкина" (3500 страниц), мы подсчитали и те страницы, где было написано и про "Пушкина", и про "Лермонтова" одновременно.

 

Тоже самое и для количества страниц, где написано про "Лермонтова" (2000 страниц). В этом числе находятся и те, в которых одновременно упоминается и про "Пушкина", и про "Лермонтова".

 

В вопросе спрашивается, сколько страниц будет по запросу "Пушкин & Лермонтов". Это обозначает, что как раз нужно найти количество страниц, где будет одновременно написано и про "Пушкина", и про "Лермонтова".

 

Отсюда получается:

 

Пушкин & Лермонтов = (3500 + 2000) - 4500 = 5500 - 4500 = 1000 страниц.

 

 

Теперь решим эту задачу с помощью Кругов Эйлера!

 

У нас всего есть две сущности: "Пушкин" и "Лермонтов". Поэтому рисуем два пересекающихся круга, желательно разными цветами.

 

 

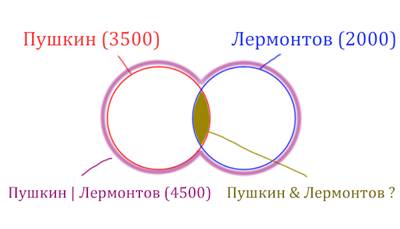
Объединение двух кругов в общую фигуру (показано фиолетовым цветом), показывает операцию "Пушкин | Лермонтов". Эта операция всегда стремится увеличить площадь, объединить площади других фигур!

 

Обратите внимание, что круги пересекаются, из-за этого сумма площадей двух кругов по отдельности (3500 + 2000 = 5500) больше чем у фигуры, которая характеризует логическую операцию «ИЛИ» "Пушкин | Лермонтов" (4500).

 

Нужно найти площадь фигуры Пушкин & Лермонтов, которая закрашена золотистым цветом. Данная логическая операция «И» стремится уменьшить площадь. Она обозначает общую площадь других фигур.

 

Найдём сначала заштрихованную часть синего круга. Она равна: площадь фиолетовой фигуры (4500) минус площадь красного круга (3500).

 

 

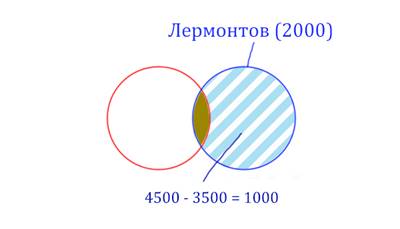
Теперь легко найти площадь золотистой фигуры. Для этого нужно от площади синего круга вычесть площадь заштрихованной части. Получается:

 

Пушкин & Лермонтов (Количество страниц) = 2000 - 1000 = 1000

 

Получается, что по запросу Пушкин & Лермонтов будет найдено 1000 страниц.

Ответ: 1000

Рассмотрим ещё одну не сложную разминочную задачу из ЕГЭ по информатике.

Задача (Разминочная)

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

 

Запрос	Найдено страниц (в тысячах)
Кокос | Ананас	3400
Кокос & Ананас	900
Кокос	2100

 

Какое количество страниц (в тысячах) будет найдено по запросу Ананас?

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

У нас две сущности: Кокос и Ананас. Нарисуем два круга Эйлера, которые пересекаются между собой. Так же отменим все имеющееся данные.

 

 

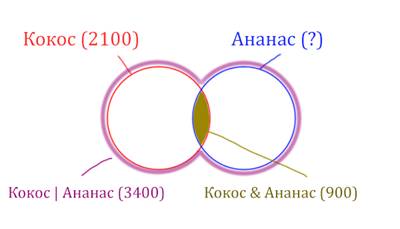
Найдём заштрихованную часть красного круга.

 

Весь красный круг 2100. Золотистая область равна 900. Заштрихованная часть равна 2100 - 900 = 1200.

 

 

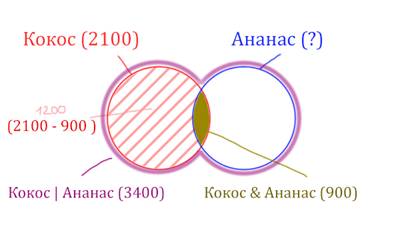
После того, как нашли заштрихованную часть (такой полумесяц), можно найти уже площадь синего круга. Для этого нужно от площади фиолетовой фигуры отнять площадь заштрихованной части!

 

Ананас (Количество страниц) = 3400 - 1200 = 2200

Ответ: 2200

Разберём классическую задачу 17 задания из ЕГЭ по информатике

Задача (Классическая)

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» - символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

 

Запрос	Найдено страниц (в тысячах)
(Космос & Звезда) | (Космос & Планета)	1100
Космос & Планета	600
Космос & Планета & Звезда	50

 

Какое количество страниц (в тыс.) будет найдено по запросу Космос & Звезда?

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

В этой задаче у нас три сущности: Космос, Планета, Звезда. Поэтому рисуем три круга Эйлера, которые пересекаются между собой.

 

Могут ли круги не пересекаться ? Могут! Если мы докажем, что площади по отдельности двух кругов в сумме дают площадь фигуры, которая получается при применении операции логического "ИЛИ".

 

 

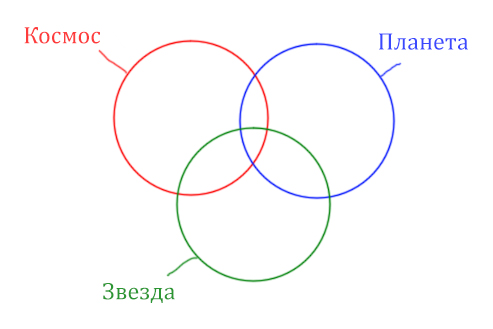
Теперь отметим на нашем рисунке запрос (Космос & Звезда) | (Космос & Планета).

 

Сначала отменим для себя то, что находится в скобках. Первое Космос & Звезда

 

 

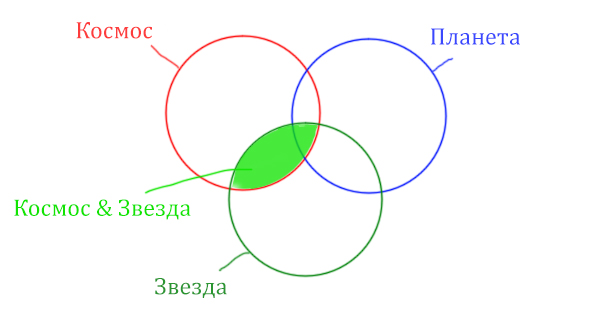
Теперь отметим вторую скобку Космос & Планета.

 

 

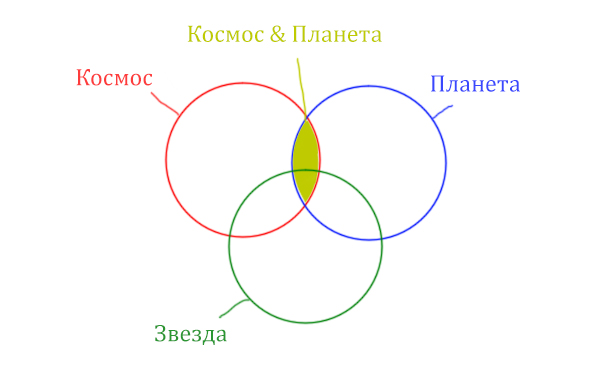
В выражении (Космос & Звезда) | (Космос & Планета) две скобки соединяет знак логического "ИЛИ". Значит, эти две области нужно объединить! Область (Космос & Звезда) | (Космос & Планета) отмечена фиолетовым цветом!

 

 

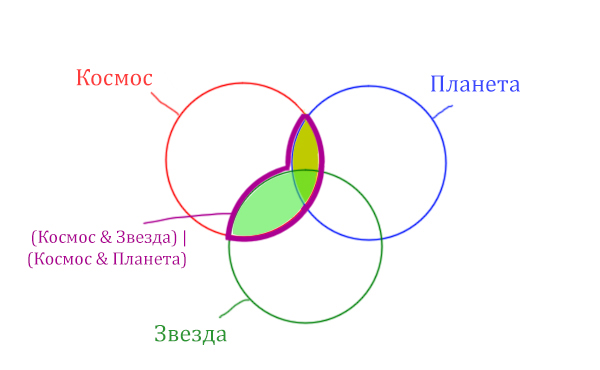
Отметим Космос & Планета ещё раз, т.к. для этого выражения известно количество страниц.

 

 

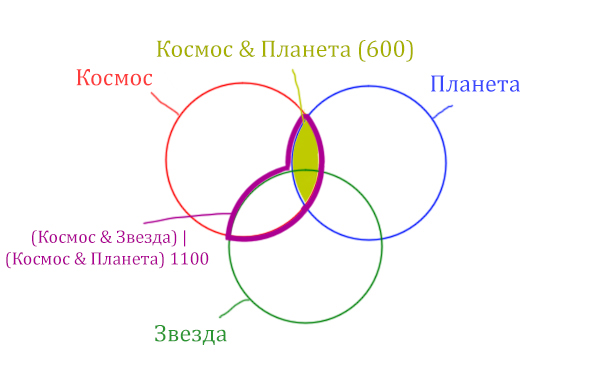
Площадь фигуры для выражения Космос & Планета & Звезда будет очень маленькая. Это общая часть для всех трёх кругов. Отметим её оранжевым цветом! Каждая точка этой фигуры должна одновременно быть в трёх кругах!

 

 

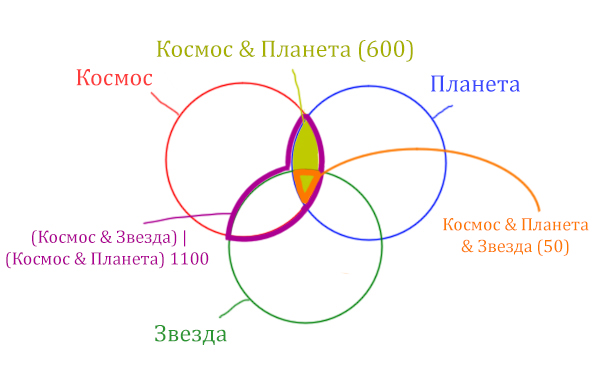
Найти нужно Космос & Звезда. Отменим на рисунке чёрным цветом ту область, которую нужно найти. Мы эту область уже отмечали салатовым цветом.

 

 

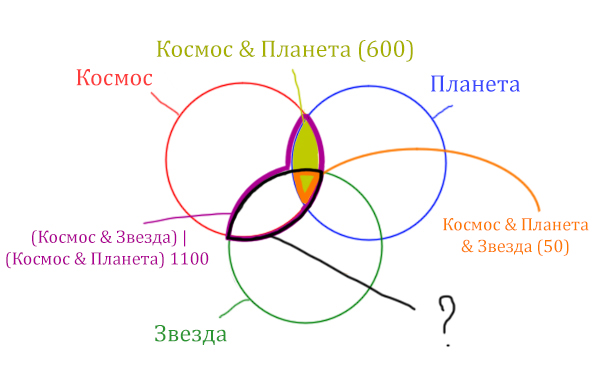
Теперь у нас есть все компоненты, чтобы решить классическую тренировочную задачу из ЕГЭ по информатике задания 17.

 

Найдём заштрихованную область.

 

 

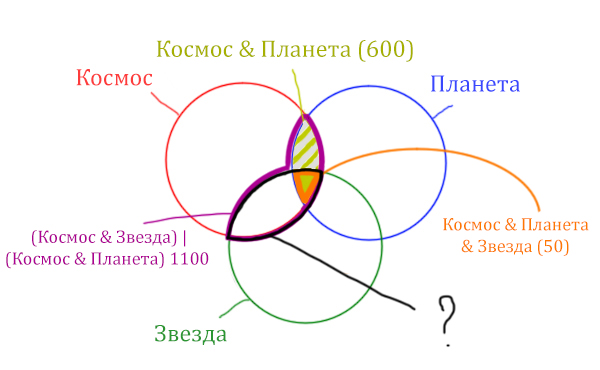
Вся область Космос & Планета равна 600. А заштрихованная часть равна: область Космос & Планета (600) минус оранжевая область (50).

 

Количество страниц в заштрихованной часте = 600 - 50 = 550

 

Тогда черная область легко находится: фиолетовая область (1100) минус заштрихованная область (550).

 

Количество страниц (при запросе Космос & Звезда) = 1100 - 550 = 550

Ответ: 550

Закрепляем материал при подготовке к 17 заданию ЕГЭ по информатике

Задача (На закрепление)

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

 

Запрос	Найдено страниц (в тысячах)
Море & Солнце	290
Море & Пляж	355
Море & (Пляж | Солнце)	465

 

Какое количество страниц (в тысячах) будет найдено по запросу Море & Пляж & Солнце? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

В задаче используются три сущности: Море, Пляж, Солнце. Поэтому нарисуем три пересекающихся круга Эйлера.

 

 

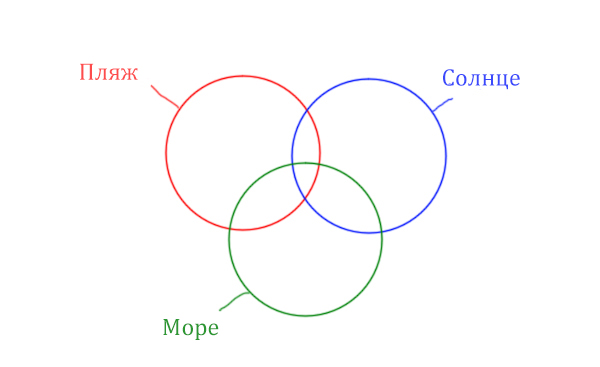
Отметим все области для которых нам даны количество страниц.

 

В начале отметим Море & (Пляж | Солнце). Для начало нарисуем область, которая в скобках (Пляж | Солнце)

 

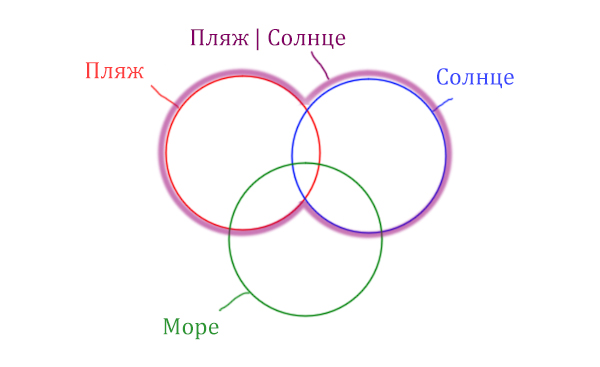
Теперь нужно очертить общую часть фиолетовой области и зелёного круга и получится Море & (Пляж | Солнце). Отметим оранжевым цветом.

 

 

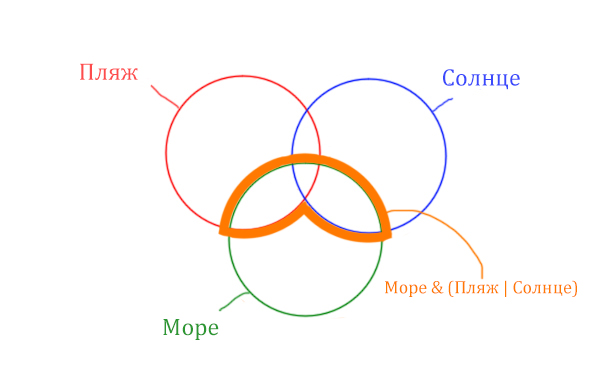
Теперь отметим Море & Пляж.

 

 

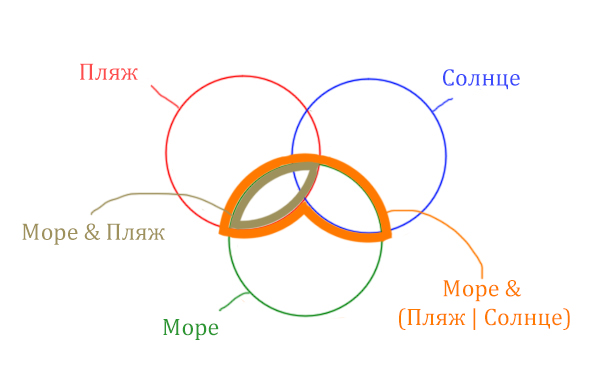
Теперь отметим Море & Солнце.

 

 

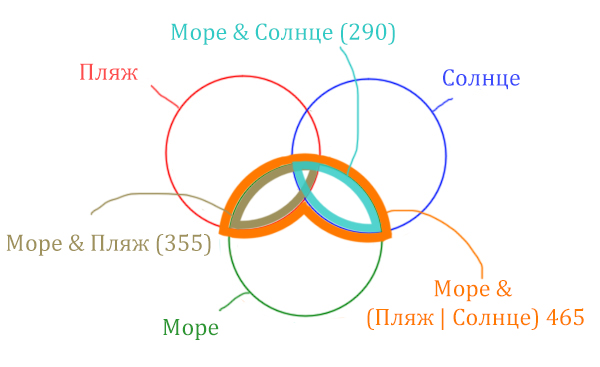
Найти нужно ту область, которая получается в результате выделения общей части для всех трёх кругов! Обозначим её чёрным цветом!

 

 

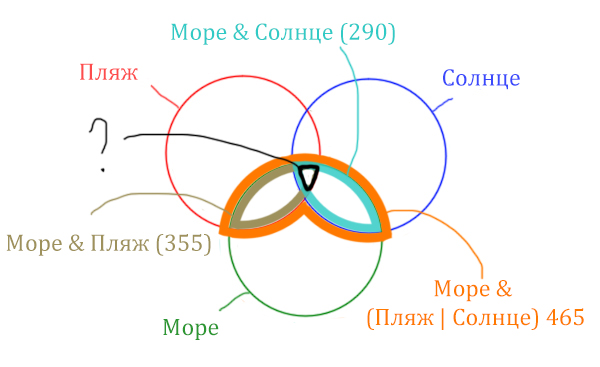
Найдём заштрихованную область!

 

 

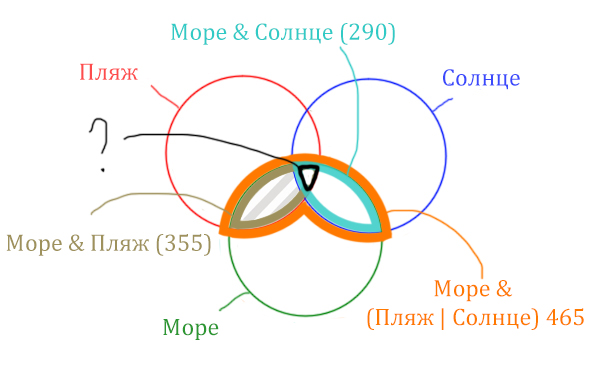
Количество страниц (в заштрихованной области) =
= Количество страниц (В оранжевой области) - Море & Солнце =
= 465 - 290 = 175

 

Чтобы найти искомую чёрную область, нужно из Море & Пляж (355) вычесть заштрихованную область (175).

 

Количество страниц (Море & Пляж & Солнце) =
= Море & Пляж (355) - Количество страниц (в заштрихованной области) 175 =
= 355 - 175 = 180

Ответ: 180

Решим ещё одну тренировочную задачу 17 задания из ЕГЭ по информатике с 4-мя сущностями!

Задача (с 4 сущностями)

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

 

Запрос	Найдено страниц (в тысячах)
Англия & (Уэльс & Шотландия | Ирландия)	450
Англия & Уэльс & Шотландия	213
Англия & Уэльс & Шотландия & Ирландия	87

 

Какое количество страниц (в тысячах) будет найдено по запросу

 

Англия & Ирландия?

 

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

Нужно нарисовать 4 пересекающихся круга. Сначала нарисуем три круга, как обычно, оставив немного места для четвёртого круга.

 

 

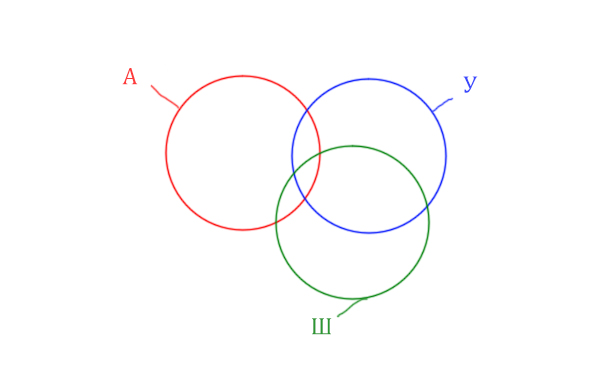
Четвёртый круг для Ирландии нужно нарисовать так, чтобы он проходил через область (Англия & Уэльс & Шотландия). Это нам подсказывает сама таблица, где есть количество страниц для Англия & Уэльс & Шотландия, а так же для Англия & Уэльс & Шотландия & Ирландия.

 

 

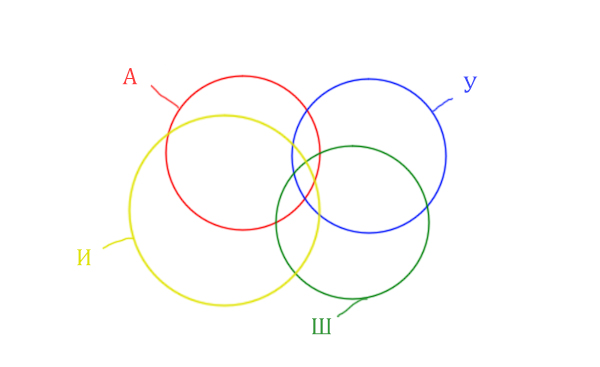
Нужно отметить на рисунке Англия & (Уэльс & Шотландия | Ирландия). Это будем делать, как всегда поэтапно.

 

Область Уэльс & Шотландия выглядит так:

 

 

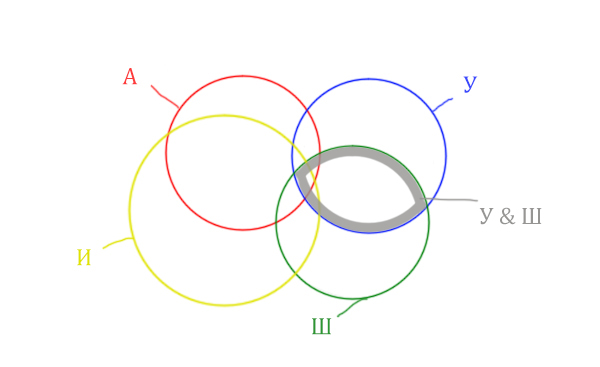
Добавим к этой области Ирландию через логическое "ИЛИ". Получается область (Уэльс & Шотландия | Ирландия). Произошло объединение серой области и жёлтого круга!

 

 

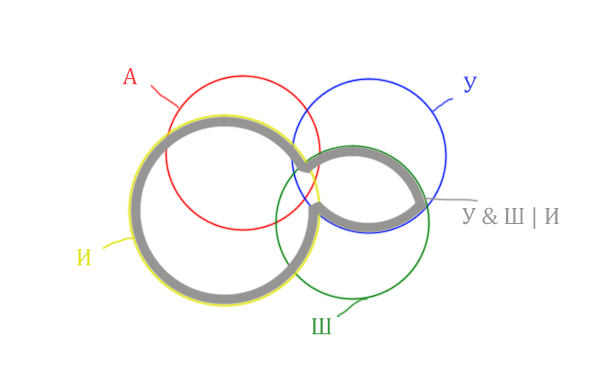
Теперь нужно сделать операцию логического "И" получившийся области с "Англией". Тогда область Англия & (Уэльс & Шотландия | Ирландия) примет вид:

 

 

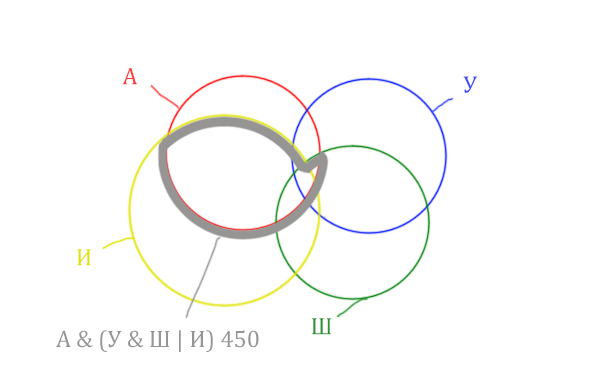
Т.е. это общее между предыдущем серым контуром и красным кругом!

 

Отметим Англия & Уэльс & Шотландия - это общая территория трёх кругов: Красного, Синего и Зелёного. Отмечено оранжевым цветом.

 

 

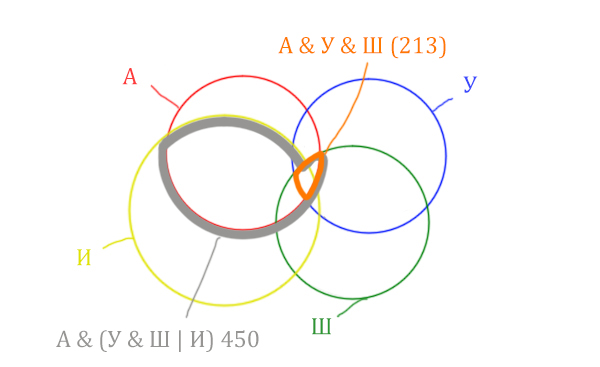
Отметим Англия & Уэльс & Шотландия & Ирландия - это общая территория четырёх кругов. Область получается ещё меньше. Если взять точку в этой области, то мы будем находится сразу в четырёх кругах одновременно. Отмечено фиолетовым цветом.

 

 

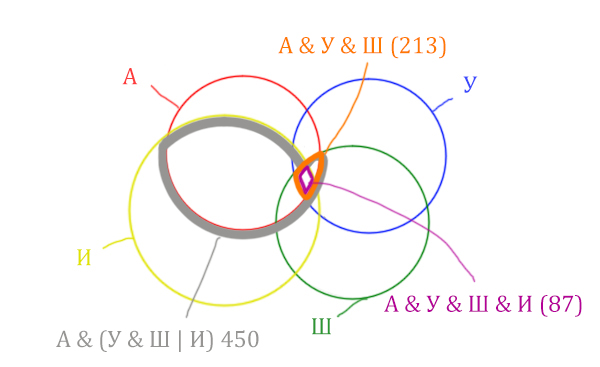
Отметим то, что нужно найти Англия & Ирландия чёрным цветом.

 

 

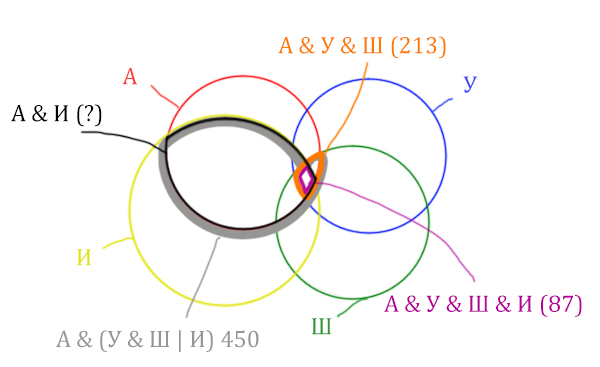
Искомую чёрную область легко найти, если из серой области вычесть кусочек, окрашенный в бирюзовый цвет!

 

 

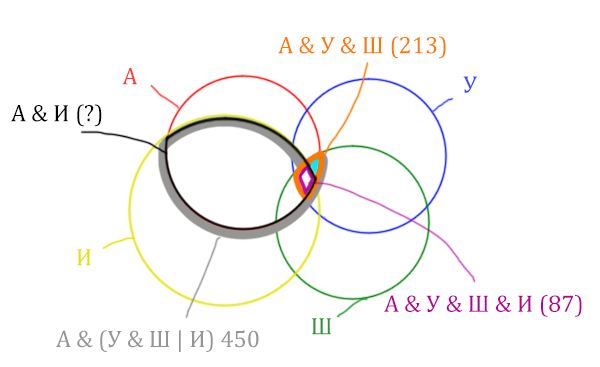
Найдём, сколько страниц приходится на бирюзовый кусочек:

 

Количество страниц (для бирюзового кусочка) =
= Англия & Уэльс & Шотландия (213) - Англия & Уэльс & Шотландия & Ирландия (87) =
= 213 - 87 = 126

 

Найдём искомую чёрную область.

 

Количество станиц (для чёрной области) =
= Англия & (Уэльс & Шотландия | Ирландия) (450) - Количество (для бирюзового кусочка) =
450 - 126 = 324

 

Это и будет ответ!

Ответ: 324.

Разберём задачу из реального экзамена по информатике, которая была в 2019 году в Москве!

Задача (ЕГЭ по информатике, 2019, Москва)

В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:

 

Запрос	Найдено страниц (в тысячах)
Суфле	450
Корзина	200
Эклер	490
Суфле & Корзина	70
Суфле & Эклер	160
Корзина & Эклер	0

 

Сколько страниц (в тысячах) будет найдено по запросу

 

Суфле | Корзина | Эклер

Решение:

Видим, что у нас три поисковых разных слова, поэтому будет три разных круга Эйлера!

 

Так же видим, что логическое "И" между словами Корзина и Эклер даёт 0 страниц. Это значит, что эти круги не пересекаются! Так же круги бы не пересекались, если бы операция логического "ИЛИ" совпадала бы с суммой этих кругов.

 

 

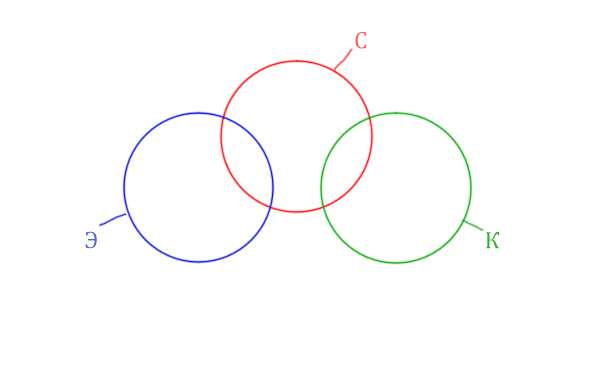
Видим, что Суфле имеет с двумя кругами пересечения, а Корзина и Эклер не пересекаются.

 

Отметим всё, что нам дано в условии.

 

 

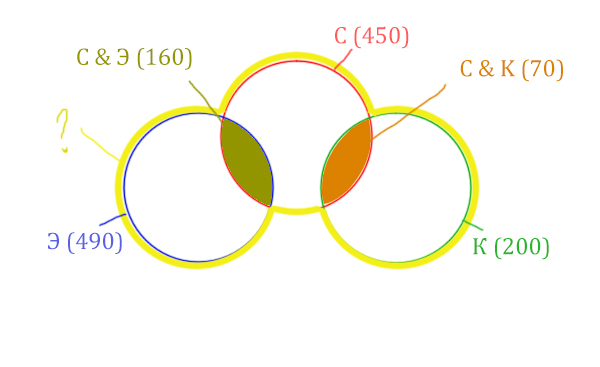
Жёлтым цветом отмечено Суфле | Корзина | Эклер . Объединение всех трёх кругов. Это то, что нужно найти.

 

 

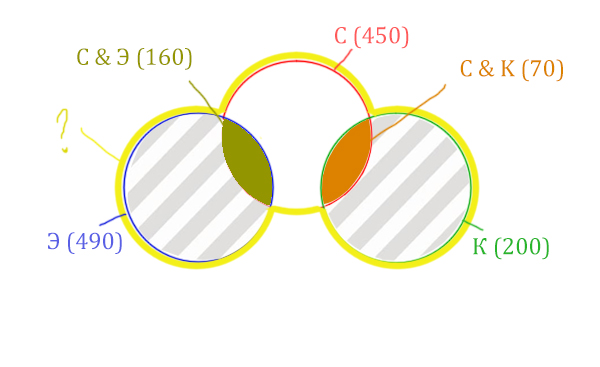
Искомая жёлтая фигура складывается из заштрихованных областей и красного круга! Площадь красного круга мы знаем. Нужно найти площади заштрихованных частей.

 

Левая заштрихованная область находится просто:

 

Количество страниц (лев. заштрих. область) =
= Эклер (490) - Суфле & Эклер (160) = 330

 

Так же найдём площадь правой заштрихованной области:

 

Количество страниц (прав. заштрих. область) =
= Корзина (200) - Суфле & Корзина (70) = 130

 

Теперь можно найти искомую жёлтую область

 

Количество страниц (Суфле | Корзина | Эклер) =
= Красный круг (450) + лев. заштрих. область (310) + прав. заштрих. область (130) =
= 450 + 330 + 130 = 910

 

Задача решена, можно писать ответ.

Ответ: 910

Разберём ещё одну задачу из реального ЕГЭ уже 2020 года

Задача (ЕГЭ по информатике, 2020, Москва)

В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:

 

Запрос	Найдено страниц (в тысячах)
Аврора	50
Крейсер	45
Заря	23
Аврора & Заря	9
Заря & Крейсер	0
Заря | Крейсер | Аврора	93

 

Сколько страниц (в тысячах) будет найдено по запросу

 

Аврора & Крейсер

Решение:

Количество страниц при запросе Заря & Крейсер равно нулю. Значит, эти два круга не будут пересекаться.

 

 

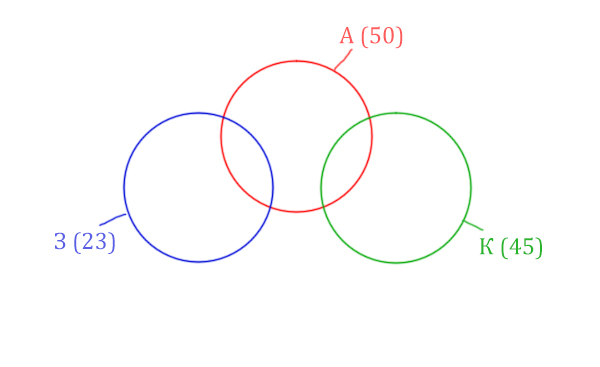
Нарисуем все данные на рисунке.

 

 

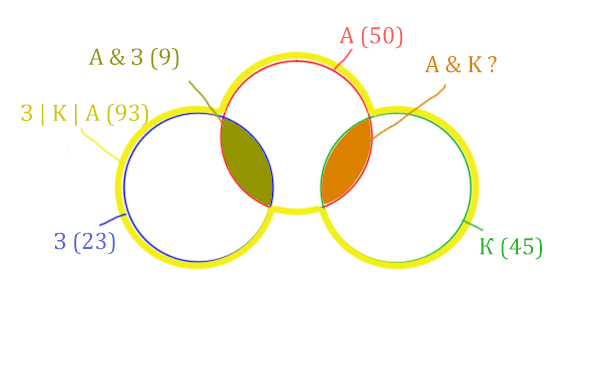
Нужно найти для начала заштрихованную правую часть.

 

 

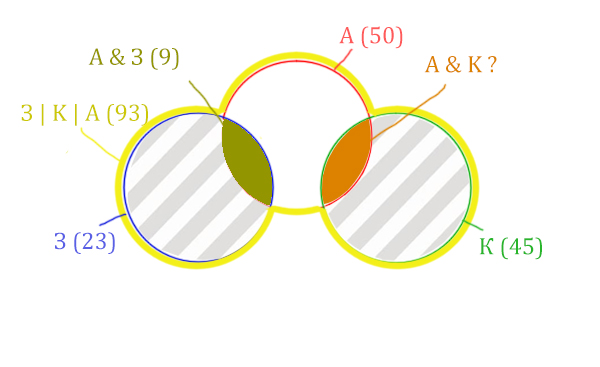
Количество страниц (для двух заштрих. частей) =
З | К | А (93) - Красный круг (50) = 43

 

Левую заштрихованную область легко найти.

 

Количество страниц (для левой заштрих. части) =
Синий круг (23) - А & З (9) = 14

 

Тогда для правой заштрихованной области получается:

 

Колич. страниц (для правой заштрих. части) =
Колич. страниц (для двух заштрих. частей) (43) - Колич. страниц (для лев. заштрих. части) (14) =
= 43 - 14 = 29

 

Тогда искомую область легко найти:

 

Колич. страниц (А & K) =
Зелёный круг (45) - Колич. страниц (для правой заштрих. части) (29) =
45 - 29 = 16

Ответ: 16