
Муниципальное казенное общеобразовательное учреждение
«Святославская средняя общеобразовательная школа»
Инновации в школьном образовании
через интеграцию математики и физики
Автор:
Попова Наталья Владимировна,
учитель математики
МКОУ «Святославская СОШ»
с.Святославка, 2019
Оглавление
Введение................................................................. …………………………3
Глава 1. Активизация познавательной деятельности обучающихся посредством интеграции предметов на примере математики и физики……………………………………………………………………………5
1.1. Потребность в возникновении интегрированных уроков………………………....5
1.2. Начальные понятия физики в 5 – 6 классах………………………………...6
1.3. Уравнения и функции – математический аппарат изучения явлений в физике……………………………………………………………………………..14
Заключение………………………………………………………………………26
Литература........................................................... …………………………...28
Приложения.......................................................... …………………………...30
Введение
Современная жизнь предъявляет к человеку новые требования. Общество нуждается в людях творчески мыслящих, любознательных, активных, умеющих принимать нестандартные решения и брать ответственность за их принятия, а также умеющих осуществлять жизненный выбор. В современных условиях, каждый учитель должен работать творчески. Это значит, проводить уроки разнообразно и увлекательно.
Урок - это основная организационная форма обучения в школе. Он является педагогической единицей процесса обучения и воспитания.
Как заинтересовать ребят изучением предметов, сделать уроки любимыми, увлекательными? Ответы на эти вопросы ищут многие педагоги, учителя.
В условиях внедрения ФГОС особое значение придаётся технологиям деятельностного обучения.
Настоящее время требует перемены мышления во многих областях жизни, внедрения в учебный процесс новых педагогических технологий. Обновление образования требует использования нетрадиционных методов и форм организации обучения, в том числе интегрированных уроков по разным предметам, в результате которых формируется деятельный подход в обучении, о котором много говорится.
Мы все сильнее осознаем причастность ко всему, что происходит на земле. Важно дать учащимся единое представление о природе, обществе и своем месте в нем, соединять в восприятии учащихся основные знания по каждому предмету в широкую, целостную картину мира.
Интеграция – (от латинского integer – целый, восстановление.) Интеграция является относительно новым веянием в образовательном процессе (это понятие в российскую педагогику пришло в 80-е годы и стало обозначать высшую форму межпредметных связей) и становится востребованным в современной школе, где развернуты активные поиски инновационных педагогических технологий.
Методика интегрированного обучения имеет цели: помочь учащимся научиться познавать, научиться жить вместе, научиться жить в ладу с самим собой.
Задача интегрированных уроков – способствовать активному и осознанному усвоению учениками учебного материала, развитию логического мышления; формирование познавательной компетенции учащихся; дать возможность использовать в ходе обучения современные интерактивные методики и объективно оценивать достижения учащихся.
Основные свойства интегрированного урока – синтетичность, универсальность. Он позволяет посвятить учащегося в конечные цели изучения не только данной темы, раздела, но и всего материала, быстрее включить его в познавательный процесс.
Интегрированные уроки эффективны независимо от того, изучают ли ученики новый или обобщают уже пройденный. На этих уроках рассматриваются многоаспектные объекты, которые являются предметом изучения различных учебных дисциплин.
Современная система образования направлена на формирование высокообразованной, интеллектуально развитой личности с целостным представлением картины мира, с пониманием глубины связей явлений и процессов, представляющих данную картину. Предметная разобщенность становится одной из причин фрагментарности мировоззрения выпускника школы, в то время как в современном мире преобладают тенденции к экономической, политической, культурной, информационной интеграции. Таким образом, самостоятельность предметов, их слабая связь друг с другом порождают серьезные трудности в формировании у обучающихся целостной картины мира, препятствуют органичному восприятию культуры. Следовательно, интеграция – инновационное средство формирования познавательной компетенции учащихся.
Глава 1. Активизация познавательной деятельности обучающихся посредством интеграции предметов на примере математики и физики
1.1. Потребность в возникновении интегрированных уроков
Приохотить ребенка к учению гораздо более
достойная задача, чем приневолить.
К.Д. Ушинский
Необходимость обращения к интегрированному обучению вызвана рядом проблем, с которыми приходится сталкиваться учителям-предметникам при реализации образовательной программы в основной и старшей школе. Заметное снижение интереса у учащихся к предметам естественно-математического цикла, которое обусловлено сложностью программного материала по физике и математике. Сама специфика предметов естественно-математического цикла побуждает к комплексному подходу в обучении школьников, т.е. логика данных наук ведёт к их интеграции, взаимопроникновению, объединению отдельных тем.
Несогласованность программ по изучаемым в школе предметам естественно-математического цикла приводит к тому, что одна и та же тема по физике и математике изучается в разное время. Эти противоречия легко снимаются в интегрированном обучении, которое позволяет решить ещё одну проблему — временную, т.е. межпредметная интеграция позволяет учителю экономить учебное время.
Чтобы научить детей думать, открывать, изобретать, учитель должен самосовершенствоваться. Учителя математики и физики, преподавая свой предмет, совсем не учитывают того, что некоторые вопросы нужно сначала изучить на уроках математики, а затем применять на уроках физики. Ещё хуже, когда математик во время объяснения новой темы совсем не говорит о её применении в физике. Математика не только дает физике вычислительный аппарат, но и обогащает её в идейном плане. На уроках математики школьники учатся работать с математическими выражениями, а задача преподавания физики состоит в том, чтобы познакомить учащихся с переходом от математических явлений к физическим и связей между ними.
1.2. Начальные понятия физики в 5-6 классах
Науку все глубже постигнуть стремись,
Познанием вечного жаждой томись.
Лишь первых познаний блеснет тебе свет,
Узнаешь: предела для знания нет.
Фирдоуси (Персидский и таджикский поэт, 940 – 1030 гг).
Рассмотрим, с какими физическими понятиями можно познакомить учащихся в процессе обучения в 5-6 классах.
Одной из приоритетных тенденций современного образования является создание межпредметных связей при изучении отдельных циклов школьных предметов. Математика имеет самые тесные межпредметные связи с физикой. На уроках математики в 5 классе учителю важно рассказать учащимся о физике, которую они начнут изучать через два года, объяснить, что для успешного изучения физики необходимы прочные знания по математике. Здесь учителю поможет книга, написанная Александром Евсеевичем Гуревичем совместно с Дмитрием Аркадьевичем Исаевым и Любовью Семеновной Понтак, «Физика и химия 5-6 класс». Данная книга поможет сформировать начальное представление о физике и химии, объяснить с научной точки зрения основные природные явления, научить обращаться с простейшими техническими устройствами.
Чтобы показать пятиклассникам значимость качественных знаний по математике для успешного изучения в дальнейшем физики, учителю на уроках математики, особое внимание необходимо уделить таким темам:
5 класс
§ «Буквенные выражения»;
§ «Формулы»;
§ «Формула площади прямоугольника»;
§ «Прямоугольный параллелепипед»;
§ «Обыкновенные дроби»;
§ «Десятичные дроби».
6 класс
• «Проценты»;
• «Пропорции»;
• «Отрицательные числа».
Рекомендуется провести эти уроки в кабинете физики.
В пятом классе во многих рабочих программах по математике рекомендовано изучать тему «Буквенные выражения» три часа. Поэтому целесообразно смоделировать из вышеизложенной разработки («Буквенные выражения») два урока, а на третьем уроке рассказать о физике – науке, которая «дружит» с математикой.
На тему «Формулы» в пятом классе отводится два часа. Рекомендуем дополнить ваши разработки следующим.
· При решении задач на движение напомните своим ученикам, что наука «физика» также изучает механические явления. Скорость, пройденный путь, время движения – это физические характеристики движущегося объекта.
· Рассматривайте встречное движение и движение в одну сторону как разные виды задач, имеющие свой алгоритм решения.
·
Отрабатывайте
навыки перевода единиц измерения длины, времени, скорости. Например: ![]() , и наоборот:
, и наоборот:![]() .
.
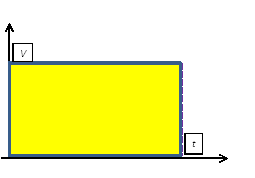
При изучении темы «Формула
площади прямоугольника» обратите внимание учеников на схожесть формул
нахождения площади (![]() ) и скорости (
) и скорости (![]() ). Если графически отобразить
скорость равномерного движения тела и время движения, то, чтобы найти
пройденный путь некоторым объектом, достаточно определить площадь полученного
прямоугольника.
). Если графически отобразить
скорость равномерного движения тела и время движения, то, чтобы найти
пройденный путь некоторым объектом, достаточно определить площадь полученного
прямоугольника.
При изучении темы «Прямоугольный параллелепипед» и «Объемы. Объем прямоугольного параллелепипеда» необходимо:
· Изучить дополнительный материал об истории открытия закона Архимеда и провести эксперимент для лучшего понимания данного закона.
· Познакомить с эталонами массы и длины, изучить историю мер единиц измерения. Целесообразно организовать изучение данного материала посредством проектной деятельности. На пример, творческие проекты «Меры измерений: от древности и до наших дней».
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
· Уделить внимание отработке навыков перевода единиц объема, показав зависимость между такими единицами, как литр, миллилитр, дециметр, сантиметр. (1 литр =1 дм3,1 мл = 1см3).
·
Ввести
понятие плотности. Плотность – это физическая величина, показывающая чему равна
масса вещества в единице объема. Научить переводить единицы плотности: ![]() . Провести эксперимент по
определению плотности вещества. Для этого понадобятся предметы небольших
размеров в форме прямоугольного параллелепипеда, электронные или рычажные весы.
Необходимо измерить массу параллелепипеда, его длину, ширину и высоту.
Вычислить объем параллелепипеда по формуле. Разделить массу на объем и так
определить плотность вещества, из которого изготовлен параллелепипед.
(Приложение 1).
. Провести эксперимент по
определению плотности вещества. Для этого понадобятся предметы небольших
размеров в форме прямоугольного параллелепипеда, электронные или рычажные весы.
Необходимо измерить массу параллелепипеда, его длину, ширину и высоту.
Вычислить объем параллелепипеда по формуле. Разделить массу на объем и так
определить плотность вещества, из которого изготовлен параллелепипед.
(Приложение 1).
|
Оборудование: предметы маленьких размеров в форме прямоугольного параллелепипеда, электронные или рычажные весы. |
|
Выполнение работы проиллюстрировать 1) Измерить массу параллелепипеда. 2) Измерить длину ширину и высоту параллелепипеда. 3) Вычислить
объем параллелепипеда по формуле 4) Разделить массу на объем и так найти плотность вещества, из которого изготовлен параллелепипед. |
Понятие десятичной дроби у пятиклассников складывается в течение всей третьей четверти. Поэтому учитель легко сможет найти время для разрешения на этих уроках таких вопросов физического характера как:
· использование десятичных и обыкновенных дробей в задачах на движение;
· выражение единиц измерения массы, длины, площади, объема и времени в дольных и кратных единицах;
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
3л = 3 дм3,
![]() .
.
· отработка навыков перевода единиц измерения скорости и плотности;
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
· решение простейших задач на движение с использованием чертежа;
Задача: За 10 минут заяц-русак пробегает путь 12 км. Определите его скорость.
![]() Дано:
Решение:
Дано:
Решение:
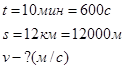
![]() .
Ответ: 20 м/с.
.
Ответ: 20 м/с.
·
сравнение
десятичных дробей как не просто чисел, а как физических измерений Например: ![]() ,
, ![]() ;
;
·
изучение
темы «Сложение и вычитание десятичных дробей» можно рассматривать
сложение и вычитание физических единиц измерения; Например: ![]() ;
;
·
рассмотрение
в качестве буквенных выражений с одной известной величиной формулы определения
пути. Например:![]() , где
, где ![]() . И, наоборот:
. И, наоборот:![]() , здесь
, здесь![]() .
.
На уроках математики при решении задач по теме «Проценты» рекомендуем ввести термин «КПД. Коэффициент полезного действия».
В учебниках по физике для
седьмого класса определение КПД звучит так: «Чтобы найти КПД механизма, надо
полезную работу разделить на ту, которая была затрачена при использовании
данного механизма». ![]() .
.
Можно решить задачу следующего содержания: «При подъеме груза массой 20 кг на 4 метра механизму необходимо иметь энергию 800 Джоулей. Чему равен КПД механизма, который совершил при этом работу равную 1000 Джоулям?». Следует сказать ученикам, что энергия затрачивается при совершении работы и обе эти величины измеряют в Джоулях. Далее в терминологию физики можно не углубляться.
Если позволяет время, то можно провести и экспериментальную работу по определению КПД. Рекомендуем сначала учителю ход эксперимента изучить из учебника по физике для 7 класса.
При изучении темы «Пропорции» в шестом классе нужно рассказать о правиле моментов и использовании рычага. Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по часовой стрелке, равен моменту силы, вращающей его против часовой стрелки, - это правило называют правилом моментов. Также описываемое пропорциональное соотношение используется при машиностроении, так понятие пропорции лежит в основе создания гидравлического пресса.
Задача: Площадь меньшего поршня гидравлической машины 10 см2, и на него действует сила в 200 Н. Площадь большого поршня равна 200см2. Какая сила действует на большой поршень?
Решение:
S1=10 см2; F1=200H; S2=200см2; F2-?
![]() ; F2·S1=F1·S2;
; F2·S1=F1·S2;
![]()
Ответ: F2= 4кН.
При изучении темы «Положительные и отрицательные числа» в 6 классе следует обратить внимание учеников на то, что в физике отрицательными числами можно описать следующее:
• температура ниже таяния льда или замерзания воды;
• скорость объекта, который движется навстречу наблюдателю;
• электрический заряд;
• ускорение тела при замедленном движении;
• время до начала наблюдения некоторого физического процесса.
«Координатная плоскость» изучается в конце темы «Положительные и отрицательные числа» и является прикладной, что вызывает у учащихся живой интерес при изучении. Общаясь друг с другом, люди часто говорят: "Оставьте свои координаты". Для чего? Чтобы человека было легко найти. Это могут быть: номер телефона, домашний адрес, место работы. Суть координат или системы координат состоит в том, что существует правило, по которому определяется положение объекта. Чтобы правильно занять свое место в кинотеатре нужно знать две координаты - ряд и место. Те, кто в детстве играл в морской бой, тоже помнят, что каждая клетка на игровом поле определялась двумя координатами - буквой и цифрой. Системы координат пронизывают всю практическую жизнь человека.
В пятом классе во многих рабочих программах по математике на изучение темы «Круговые диаграммы» отводится два часа. В шестом классе тему «Столбчатые диаграммы» изучают также два часа.
В шестом классе можно построить столбчатую диаграмму при описании движения и обратить внимание учеников на то, что зависимость можно показать и с помощью графика, и с помощью диаграммы.
Например, «На соревнованиях по плаванию в 50-метровом бассейне спортсмен проплыл 100-метровую дистанцию. На рисунке изображен график зависимости расстояния между спортсменом и точкой старта от времени движения спортсмена. Постройте соответствующую диаграмму».
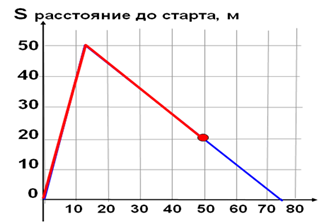
Решение:
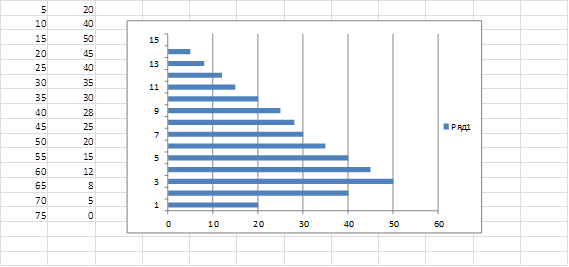
Использование межпредметных связей не только поможет показать взаимосвязь между предметами, подготовить учащихся к изучению физики, но и разнообразит уроки математики, расширит их практическую направленность.
1.3.Уравнения и функции – математический аппарат изучения явлений в физике
Математика – наука прикладная. Функции прямой и обратной пропорциональностей можно почти одновременно изучить как на уроках алгебры, так и на уроках физики в 7-8 классах. При изучении данных тем необходимо еще раз обратить внимание учащихся на то, что с увеличением аргумента значение функции обратной пропорциональности уменьшается.
Прямолинейное равномерное движение можно описать при помощи графика линейной функции. Рассмотрим задачу, которую можно предложить семиклассникам при изучении линейных функций на уроках алгебры.
Задача. Пешеход движется равномерно со скоростью 4 км/ч из пункта А в пункт В. Задайте формулой зависимость расстояния S, пройденного пешеходом от времени t.
Решение: S = 4t
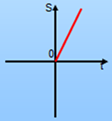
Задача. Автобус и мотоциклист движутся навстречу друг другу со скоростями 10м/с и 20 м/с. Расстояние между ними в момент начала наблюдения равно 500 м. Считая, что ось Х направления в сторону движения автобуса и при t=0 положение автобуса совпадает с началом отсчета, написать для автобуса и мотоциклиста уравнения х=х(t).
Решение.
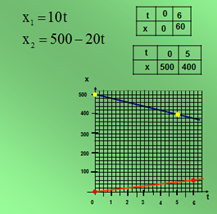
Формулу силы тяжести F=mg, можно получить, выполнив на уроке эксперимент и построив график зависимости F(m).
|
|
Оборудование: динамометр, 5 грузов по 100 гр., миллиметровая бумага. |
||||||||||||
|
1 |
Подвешиваем на динамометр по отдельности грузы и фиксируем силу тяжести. |
||||||||||||
|
2 |
Данные заносим в таблицу.
|
||||||||||||
|
3 |
По получившимся данным строим график зависимости силы тяжести F от массы тела m.
|
||||||||||||
|
4 |
Зависимость силы тяжести от массы груза является прямо пропорциональной. Коэффициент пропорциональности, k (ка) определим, как отношение силы тяжести к массе груза.
g- ускорение свободного падения |
Знания линейных функций будут необходимы при выполнении лабораторной работы «Изучение зависимости силы упругости от деформации тела» для более наглядного представления прямо пропорциональной зависимости между физическими величинами.
Для проведения работы понадобятся пружина и 4 грузика по 102 грамма.
1. Измерим длину нерастянутой пружины.
2. Подвесим один грузик массой 0,1 кг к пружине и снова измерим длину пружины.
3. Подвесим второй грузик, теперь масса груза на пружине составляет массой 0,2 кг, измерим длину пружины.
4. Подвесим третий грузик и измерим длину пружины, которая растянулась под действием груза массой 0,3 кг
5. Подвесим еще грузик и получим груз массой 0,4 кг, подвешенный на пружине; измерим длину пружины
Построим график зависимости F от l. На координатной плоскости отметим точки… Соединим получившиеся точки… Графиком данной зависимости является - прямая.
Мы знаем, что кроме силы тяжести направленной вертикально вниз на тело действует и сила упругости, направленная вертикально вверх в нашем случае сила тяжести грузов, подвешенных к пружине, уравновешивается силой упругости, возникшей в пружине.
|
|
|
Линейные функции можно использовать при изучении темы «Плотность».
Задача. Записать формулу зависимости массы стальной балки от её объема, если V – объем балки, m - его масса, плотность стали 7,8. Построить график этой зависимости.
Решение: m=ρV; ρ=7,8; m =7,8V; у=k·х;
![]()
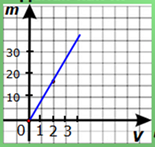
Многие реальные ситуации моделируют с помощью прямой пропорциональности. Например, Рассмотрим уравнение S=2t. Если принять, что это формула расстояния: S= V t , то можно предложить построить график этого уравнения и найти по графику путь, пройденный за 4 секунды?
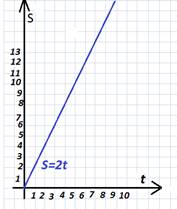 Решение:
Решение:
|
t( сек) |
1 |
2 |
3 |
|
S(м) |
2 |
4 |
6 |
По уравнению у = 0,5х + 4 можно описать движение. Здесь движущееся тело находится на расстоянии 4 метров от наблюдателя спереди и отдаляется от него со скоростью 0,5 м/с. Можно также построить график и провести анализ.
При изучении на уроках алгебры линейных и квадратных уравнений учителю желательно использовать физические задачи, что позволит впоследствии применять полученные знания на уроках физики. Для этого необходимо показать различие и сходство при решении задачи математическим и физическим способами.
Решим следующую задачу.
В лесу мимо пня, на котором сидела Маша, в 10 часов 00 минут пробежал Медведь со скоростью 0,9 км/ч. Через некоторое время в 10 часов 06 минут Маша пустилась в погоню за Медведем со скоростью 1,8 км/ч. Сколько времени понадобится Маше, чтобы догнать Медведя?
Рассмотрим математический способ решения:
- Для решения данной задачи нам понадобится таблица.
|
|
υ, км/ч |
t, ч |
S, км |
|
|
Медведь |
|
|
|
|
|
Маша |
|
|
|
|
Определим:
- Какая физическая величина известна?
- Какой путь S, пробежал каждый?
- Что можно сказать о времени t? (время движения Маши на 6 мин меньше)
- Как можно выразить 6
мин в часах? ![]()
- Какое время возьмем за х? (наименьшее – время движения Маши)
- Тогда какое время был в пути Медведь? (на 0,1 ч больше, т.е. х+0,1 ч)
Заполним таблицу. Нам известна скорость объектов, известно, что путь, который пробежали Маша и Медведь, одинаков. Время движения Маши на 6 минут меньше, чем у Медведя. Выразим 6 мин в часах. Пусть х – время движения Маши, тогда время движения Медведя х+1. Определим расстояние, которое пробежала Маша: S1 = 1,8 х. Определим расстояние, которое пробежал Медведь: S2 = 0,9( х+0,1). Т.к. S1= S2, то 1,8х =0,9(х+0,1). Решим данное равенство и найдем х. х=0,1 часа.
|
|
υ, км/ч |
t, ч |
S, км |
|
|
Маша |
|
х ч |
S1, км |
S1= S2 |
|
Медведь |
|
|
S2, км |
|
1,8х =0,9(х+0,1)
1,8х –0,9 х – 0,09 = 0
0,9х – 0,09 = 0
0,9х = 0,09
х = 0,09/0,9
х = 0,1 часа – время Маши
Ответ: Время Маши – 0,1 часа.
Запишем физический способ решения задачи.
|
Дано:
|
СИ:
|
Решение:
Ответ: |
|
|
Учащимся можно предложить составить задачу по рисунку и решить её математическим и физическим способами,
54
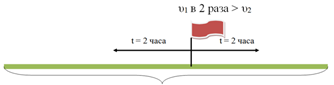
Математический способ решения
|
|
υ, км/ч |
t, ч |
S, км |
|
|
I |
2х |
2 ч |
4х км |
|
|
II |
х |
2 ч |
2х км |
|
Составляем уравнение
4х + 2х = 54
6х = 54
х = ![]() км/ч
км/ч
2х = 2∙9 = 18 км/ч
Ответ: Через 2 часа скорость первого равна 18 км/ч и скорость второго - 9 км/ч.
Физический способ решения.
|
Дано:
|
СИ:
7200 с 54000 м
|
Решение:
Ответ: через 2 часа скорость первого равна 5 м/с и скорость второго – 2,5 м/с. |
|
|
используя алгоритм:
Линейные функции применяются во многих физических процессах:
- в кинематике – это графики пути, перемещения, координаты прямолинейного равномерного движения; скорости, ускорения при прямолинейном равнопеременном движении;
- в динамике - графики зависимости Fтяж (m), Fтр (P), Fупр (x),…
- в разделе «законы сохранения» - графики зависимостей Еп(h), W(t), p (t),…
- в квантовой физике - графики Екин (частота падающего света) в теории фотоэффекта.
На первых уроках по физике в 7 классе учитель обычно раскрывает смысл физический явлений, рассказывает о том, что физика – наука, которая изучает физические явления и процессы. Физика для исследования физических процессов использует математический аппарат исчисления. Нужно подвести детей к тому, что им придется изучить много формул, описывающие физические процессы. И здесь учителю необходимо раскрыть смысл записи больших и малых чисел в стандартном виде. (Приложение 2)
Так как дети еще с пятого
класса по математике знают формулу ![]() , то для
постановки проблемного вопроса на уроке математике при изучении темы
«стандартный вид числа» в 8 классе, можно дать задачу с большими величинами, решаемую
с помощью этой формулы. Например:
, то для
постановки проблемного вопроса на уроке математике при изучении темы
«стандартный вид числа» в 8 классе, можно дать задачу с большими величинами, решаемую
с помощью этой формулы. Например:
Задача: расстояние от Земли до
солнца 150000000 км. За сколько секунд свет от Солнца дойдет до Земли, если
скорость света 300000 ![]() .
.
Решение: Воспользуемся
известным определением: расстояние, прошедшее движущимся телом за единицу
времени называется скоростью. Значит, нам нужно 150 миллионов километров
поделить на 300 тысяч километров. 150 миллионов в стандартной записи имеет вид:
![]() , то есть
150 000 000 =15
, то есть
150 000 000 =15 ![]() 10 000 000=
10 000 000=
![]() . Таким же образом запись
3 000 000 в стандартном виде будет таким:
. Таким же образом запись
3 000 000 в стандартном виде будет таким:![]() . Несколькими уроками
ранее учащиеся изучили действия со степенями:
. Несколькими уроками
ранее учащиеся изучили действия со степенями: ![]() Итак, решение задачи:
Итак, решение задачи:
![]() Дано:
Решение:
Дано:
Решение:
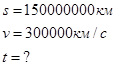
![]()
Если учитель хочет рассмотреть эту задачу на первых вводных уроках по физике, то ему придется объяснить детям тему «Действия со степенями», которую они будут изучать на уроках математики в 8 классе.
|
При умножении степеней с одинаковыми основаниями показатели степени складываются. |
|
|
При делении степеней с одинаковыми основаниями показатели степени вычитаются. |
|
|
При возведении степени в степень показатели степени перемножаются. |
|
В восьмом классе по математике при изучении темы «Стандартный вид числа» предлагаем ввести названия больших малых чисел и сразу после введения определения «стандартный вид числа»:

|
|
Количество нулей |
|
|
миллион |
6 |
106 |
|
миллиард |
9 |
109 |
|
триллион |
12 |
1012 |
|
квадраллион |
15 |
1015 |
|
квинтиллион |
18 |
1018 |
|
Секстиллион |
21 |
1021 |
|
октиллион |
27 |
1027 |
|
нониллион |
30 |
1030 |
|
дециллион |
33 |
1033 |
Чтобы ввести понятие малых чисел, предлагаем решить следующую задачу.
Задача. Масса Земли приближенно равна 6 000 000 000 000 000 000 000 т, а масса атома водорода 0,0000000000000000000017 г. Во сколько раз Земля тяжелее атома водорода?
Дано:
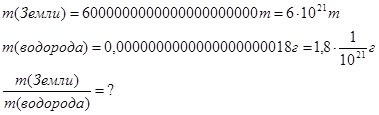
Решение:
Вначале ученикам нужно объяснить, что а в степени минус эн равен обратной величине а в степени эн. Хотя по учебнику Макарычева Юрий Николаевича эта формулу рассматривают в 9 классе. А на уроках физики дети с ней сталкиваются, как только начинают решать серьезные задачи.
Итак, вводим формулу: ![]() .
.
![]() .
.
![]() .
.
Вспомним, что при делении степеней с одинаковыми основаниями показатели степени вычитаются.
![]()
Даже на вводных уроках по физике бывает так, что учитель не обращает внимания на то, что дети не знают приставок СИ, что их надо запомнить, как таблицу умножения, «на века». Так хотя бы на уроках математики, при изучении темы «стандартное число» или «действия со степенями» необходимо эти приставки заучить наизусть.
|
|
Приставка Обозначение |
||||
|
Десятичный множитель |
русская |
международная |
русское |
международное |
Пример |
|
101 |
дека |
deca |
да |
da |
дал — декалитр |
|
102 |
гекто |
hecto |
г |
h |
гПа — гектопаскаль |
|
103 |
кило |
kilo |
к |
k |
кН — килоньютон |
|
106 |
мега |
Mega |
М |
M |
МПа — мегапаскаль |
|
109 |
гига |
Giga |
Г |
G |
ГГц — гигагерц |
|
1012 |
тера |
Tera |
Т |
T |
ТВ — теравольт |
|
1015 |
пета |
Peta |
П |
P |
Пфлопс — петафлопс |
|
1018 |
экса |
Peta |
Э |
E |
ЭБ — эксабайт |
|
1021 |
зетта |
Exa |
З |
Z |
ЗэВ — зеттаэлектронвольт |
|
1024 |
йотта |
Zetta |
И |
Y |
ИБ — йоттабайт |
|
|||||
|
Десятичный множитель |
Приставка |
Обозначение |
|||
|
русская |
международная |
русское |
международное |
Пример |
|
|
10−1 |
деци |
deci |
д |
d |
дм — дециметр |
|
10−2 |
санти |
centi |
с |
c |
см — сантиметр |
|
10−3 |
милли |
milli |
м |
m |
мH — миллиньютон |
|
10−6 |
микро |
micro |
мк |
µ (u) |
мкм — микрометр, микрон |
|
10−9 |
нано |
nano |
н |
n |
нм — нанометр |
|
10−12 |
пико |
pico |
п |
p |
пФ — пикофарад |
|
10−15 |
фемто |
femto |
ф |
f |
фс — фемтосекунда |
|
10−18 |
атто |
atto |
а |
a |
ас — аттосекунда |
|
10−21 |
зепто |
zepto |
з |
z |
зКл — зептокулон |
|
10−24 |
йокто |
yocto |
и |
y |
иг — йоктограмм |
Для закрепления предлагаем следующую задачу.
Задача: Пересчитать длину волны 0,45 микрометров в метры и нанометры.
Решение:
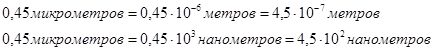
Интегрированные уроки призваны расширить знания учащихся по определенным темам. Они совершенствуют структуру межпредметных связей и помогают повысить воспитательную эффективность урока, ломают сложившуюся диспропорцию между интеллектуальным и эмоциональным познанием, соотношением логики и эмоций.
Заключение
Итак, процесс интеграции возник не на пустом месте. Это длительный этап становления, представляющий собой высокую форму воплощения межпредметных связей на качественно новой ступени обучения, способствующей созданию нового целого «монолита» знаний.
Интеграция учебных предметов – далеко не механическая деятельность, а интегрированный учебный предмет не простая сумма отдельных учебных курсов. Этот процесс требует существенных изменений в содержании, структуре учебных предметов, усилений в них общих идей и теоретических концепций.
Возможность различных форм интеграции, таких как полное слияние учебного материала, с выделением специфических глав; построение автономных блоков с самостоятельными программами или разделами общей программы, самостоятельными учебниками и методиками позволит более рационально подойти к процессу обучения и воспитания в современной школе, целью которого является формирование целостного представления мира у школьников.
Основной формой организации процесса интеграции предметов в школе является интегрированный урок, особенностью которого выступает тот факт, что его могут вести два или три, а может быть и больше учителей. С психолого-педагогической точки зрения интегрированный урок способствует активизации познавательной деятельности школьников, стимулирует их познавательную активность, является условием успешного усвоения учебного предмета и формирует познавательную компетенцию учащихся.
Что дает данная работа учителю?
· Рождение нового уровня мышления – глобального, интегрированного, а не замкнутого в своей узкой специализации.
· Освобождает учебное время для изучения другого явления.
· Исключает дублирование учебного материала.
· Усиление межпредметных связей.
Что дает данная работа ученику?
· Активизация мыслительной деятельности.
· Интенсификация учебного материала.
· Расширение сферы получаемой информации.
· Подкрепление мотивации в обучении.
· Умение сопоставлять и анализировать отдельные явления с различных точек зрения, рассматривать их в единстве взглядов.
· Снижение перегрузок.
Кроме того, интеграция обеспечивает совершенно новый психологический климат для ученика и учителя в процессе обучения.
Необходимо знать, что интеграция возможна только при ряде условий: родстве наук, соответствующих интегрируемым учебным предметам; совпадении и близости объекта изучения; наличии общих методов и теоретических концепций построения.
Педагогическая деятельность - это сплав нормы и творчества, науки и искусства. Поэтому важно интегрировать, правильно сочетать то разнообразие приёмов учебной деятельности, которое существует. От этого будет зависеть успех, а значит и результат обучения и здоровья детей
В профессиональной деятельности учителя всегда есть простор для поиска, педагогического творчества и уже не на уровне традиционной методики, а на уровне интеграции знаний по предметам.
Таким образом, можно утверждать, что интеграция - средство формирования познавательной компетенции учащихся, реальная потребность времени, необходимая для формирования успешной личности. Интеграция востребована для инновационных методов в процессе обучения и воспитания.
Литература
1. Алгебра. Тесты для промежуточной аттестации. 7-8 класс / Под ред. Ф.Ф. Лысенко. – Ростов – на – Дону: Легион – М, 2009. – 224с.
2. Алгебра: Учебник для 7 кл. общеобразоват. учреждений /Ю.Н.Макарычев, Н.Г. Миндюк и др.– М.: Просвещение, 2014. – 240с.
3. Выговская В.В. Поурочные разработки по математике: 6 класс. – М.: ВАКО, 2008. – 544с.
4. Власова Т.Г. Предметная неделя математики в школе. – Ростов н/д.: Феникс, 2006. – 176с.
5. Горлова Л.А. Интегрированные уроки физики. 7-11 классы.– М.: Издательство «Экзамен», 2010. - 144с.
6. Ерина Т.М. Поурочное планирование по алгебре. 7 класс: к учебнику Ю.Н. Макарычев и др. «Алгебра: 7 класс». –М.: «Экзамен», 2006.-253 с.
7. Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 6 класса. - М.: ИЛЕКСА, 2009. – 176с.
8. Ершова А.П., Голобородько В.В., Ершова А.С. Самостоятельные и контрольные работы по алгебре и геометрии для 7 класса. – М.: Илекса, 2016. – 208с.
9. Лакоценина Т.П. Современный урок. Интегрированные уроки. [Текст] Научно-практич. пособие для учителей, руковод. учебн. заведений, студентов пед. учеб. заведений, слушателей ИПК. – Ростов – н/Д: Изд-во «Учитель», 2008. – 256с.
10. Математика. 5-11 классы: уроки учительского мастерства / Е. В. Алтухова и др. – Волгоград: Учитель, 2009. – 299с.
11. Математика 6 класс: поурочные планы по учебнику Н.Я. Виленкина, В.И. Жохова. Первое полугодие/авт-сост. Л.А.Тапилина,Т. Л. Афанасьева. – Волгоград: учитель, 2006. – 173с.
12. Математика 6 класс: поурочные планы по учебнику Н.Я. Виленкина, В.И. Жохова. Второе полугодие/авт-сост. Л.А.Тапилина,Т. Л. Афанасьева. – Волгоград: учитель, 2006. – 173с.
13. Методическое пособие по математике для учащихся 5-6 класса/ Сост. Г.В. Королькова. – Волгоград: Учитель, 1998.- 106с.
14. Математика. 5 класс: учеб. для общеобразоват. учреждений/ Н.Я. Виленкин и др. – М.: Мнемозина, 2011. – 280 с.
15. Математика. 6 класс: учеб. для общеобразоват. учреждений/ Н.Я. Виленкин и др.: - М.: Мнемозина, 2013. – 288 с.
16. Перышкин. А.В. Физика. 7 класс. Учебник для общеобразовательных учреждений. Вертикаль. ФГОС. - М.: Дрофа, 2013 г.
17. Попова Л.П. Поурочные разработки по математике. К учебному комплекту Н.Я.Виленкина и др. 5 класс - М.:ВАКО, 2011.
18. Попов М. А. Контрольные и самостоятельные работы по математике: 5 класс: к учебнику Н.Я. Виленкина и др. «Математика.5 класс». – М.: «Экзамен», 2009. – 127с.
19. Рурукин, А.Н. Поурочные разработки по алгебре: 7 класс. – М.:ВАКО, 2006 – 416 с..
20. Сборник задач по физике: 7-9 кл.: к учебникам А.В.Перышкина и др. «Физика 7 класс», «Физика 8 класс», «Физика 9 класс» / А.В.Перышкин; сост. Г.А.Лонцова. – 9-е изд., перераб. и доп. – М.: Издательство «Экзамен», 2013. – 269, (3) с.
Образовательные ресурсы Интернета:
1. Физика: http://www.alleng.ru/edu/phys.htm
2. Физика в школе: http://w3.ivanovo.ac.ru/phys/school.htm
3. "Школьная физика для учителей и учеников"alsak.ru
Приложения
Приложение 1
Форма урока: Открытый интегрированный урок
математики и физики. 5 класс.
Тип урока: Урок изучения нового материала.
Тема: «Объемы. Объем прямоугольного параллелепипеда»
Оборудование: ПК, проектор, модели параллелепипеда и куба, лабораторное оборудование (мензурка, стакан с водой, тела неправильной формы)
Цель урока: Организация условий достижения учащимися образовательных результатов по заданной теме:
· приобретение учебной информации;
· закрепление усвоения информации;
· контроль усвоения информации;
· приобретение новых умений и навыков, применение их на практике;
· формирование УУД (регулятивных, познавательных, коммуникативных).
Задачи:
Образовательные:
· Дать понятие объёма, единицы измерения объема;
· Сформировать знания об объёмах различных фигур;
· Научить находить объём параллелепипеда и куба по формулам;
· Научить опытным путем находить объем параллелепипеда и объем тел неправильной формы.
Развивающие:
· Содействовать развитию у школьников логического мышления, математической речи;
· Способствовать развитию познавательного интереса;
· Развивать навыки самоконтроля и самооценки достигнутых знаний и умений;
· Развивать умение анализировать, сравнивать, выявлять закономерности, обобщать;
· Расширить математический кругозор.
Воспитательные:
· Воспитывать ответственное отношение к учебному труду, активность, самостоятельность;
· Показать значение математических знаний в жизни, побудить к применению этих знаний в жизненных ситуациях.
· Показать практическую связь математики и физики.
Формируемые УУД:
· Регулятивные: умение ставить цель урока, определять его задачи; составлять план действий на уроке; объективно оценивать правильность выполнения своих действий на уроке. Планировать свои действия в соответствии с поставленными задачами, вносить коррективы в свои действия с учетом сделанных ошибок. Осознание того, что усвоено и что еще нужно усвоить.
· Коммуникативные: умение работать в паре, группе, умение слушать и слышать одноклассников и учителя, умение высказывать свое мнение в виде развернутых предложений.
· Познавательные: умение ориентироваться в системе знаний, добывать новые знания, находить ответы на вопросы, используя свой жизненный опыт и информацию, полученную на уроке.
· Достижение планируемых образовательных результатов (предметных, метапредметных, личностных).
Планируемые образовательные результаты:
1.Предметные:
ü Знать: единицы измерения, формулу объема параллелепипеда и куба, вычисление объема фигур правильной и неправильной формы опытным путем.
ü Понимать: необходимость важности единиц измерения и объема при решении учебных и практических задач.
ü Уметь: применять полученные знания в повседневной жизни.
2.Метапредметные:
Регулятивные:
ü Постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимся, и того, что еще неизвестно.
ü Выбор, принятие и сохранение учебной цели и задачи.
ü Составление плана, осуществление самоконтроля, взаимоконтроля и самооценки, осознание качества и уровня усвоения.
ü Приёмы саморегуляции.
Познавательные:
ü Сравнение, обобщение, конкретизация, анализ; самостоятельное выделение и формулирование познавательной цели; поиск и выделение необходимой информации, применение методов информационного поиска, в том числе с помощью компьютерных средств.
ü Умение структурировать знания; умение осознанно и произвольно строить речевое высказывание в устной и письменной форме; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.
Коммуникативные:
ü Умение формулировать собственное мнение и позицию.
ü Осознанное построение речевых высказываний.
ü Восприятие выступлений учащихся.
ü Участие в обсуждении содержания материала.
ü Взаимоконтроль, взаимопроверка, распределение обязанностей в группе.
ü Планирование учебного сотрудничества с учителем и сверстниками – определение цели, функций участников, способов взаимодействия.
3.Личностные
ü Рефлексия собственной деятельности.
ü Действие смыслообразования, т. е. установление учащимися связи между целью учебной деятельности и ее мотивом.
ü Информационная культура учащихся, внимательность, аккуратность, дисциплинированность, усидчивость
Ход урока:
1. Приветственное слово учителя. Проверка готовности учащихся к уроку.
Сегодня, дорогие ребята, мы отправимся в удивительный мир знаний.
Для того чтобы открыть двери в этот мир, я попрошу вас выполнить следующие задания. На слайде (слайд 2) представлены различные единицы измерения. Распределите данные единицы измерения на 4 группы и каждой группе дайте название (дети работают самостоятельно). Итак, давайте проверим, какие группы вы получили, и какие единицы измерения к ним отнесли (слайд 3). Единицы измерения массы (кг, ц, т), единицы измерения длины (см, м, км), единицы измерения площади (а, га, дм2). Посмотрите оставшиеся единицы измерения - м3 дм3 см3. Вспомните и скажите, как называются данные единицы измерения? (Если у детей возникло затруднение, учитель сам дает название четвертой группе).
Итак, ребята, попробуйте сформулировать тему сегодняшнего урока (учащиеся пытаются сформулировать тему урока) (слайд 4)
2.Объяснение нового материала.
Приобретая аквариум, начинающие аквариумисты населяют его по принципу «Чем больше рыбок, тем лучше», но потом удивляются, почему рыбки начинают погибать (слайд 5). Оказывается, существуют нормы объема воды на каждую рыбку, которые зависят от размера рыбок. Я ставлю перед вами задачу: «Выяснить, достаточен ли объем аквариума для тех рыбок, которые в нем живут? А в аквариуме живут 6 рыбок по 2 см длиной, 5 рыбок по 5 см длиной, 3 рыбки по 7 см длиной».
Посмотрите на аквариум (слайд 5).
Какую геометрическую фигуру он вам напоминает? (прямоугольный параллелепипед)
Что мы знаем про прямоугольный параллелепипед? Какие три измерения есть у прямоугольного параллелепипеда. Назовите их (длина, ширина, высота).
Решение задачи. Давайте сначала определим, какой объем воды необходим для наших рыбок (слайд 6).
Для решения задачи потребуется следующий справочный материал (слайд 7).
|
Размер рыбки |
Необходимый объем воды |
|
До 3 см |
1 литр |
|
До 5 см |
2 литра |
|
До 8 см |
3 литра |
|
До 10 см |
4 литра |
|
Больше 12 см |
10 литров |
6х1=6 литров для 6 рыбок длиной 2см
5х2=10 литров для 5 рыбок длиной 5см
3х3=9 литров для 3 рыбок длиной 7см
6+10+9=25 литров воды понадобится для всех рыбок.
Ребята, а как нам определить, сколько воды нужно для того, чтобы заполнить аквариум?
Так как мы с вами выяснили, что аквариум имеет форму прямоугольного параллелепипеда, а его измерения – длина, ширина, высота, то перемножив все измерения, мы сможем определить его объем.
Для обозначения объема используется латинская буква V
V=АхВхС.
Vаквариума=40х40х80=128000 см3
Мы с вами определили объем аквариума, объем воды необходимой для наших рыбок, но не ответили на главный вопрос задачи: « Достаточен ли объем воды в аквариуме для наших рыб?» Решая задачу, мы получили объемы в литрах и см3
(слайд 8) Давайте переведем 128000см3 в литры. 128000 см3 =128 литров.
Сделайте вывод: « Достаточен ли объем воды в аквариуме для наших рыб?» (да)
Учитель показывает учащимся модель куба.
Можно ли использовать данную формулу для нахождения объема куба?
Покажите все измерения куба, какие они?
Давайте выведем формулу для вычисления объема куба. Так как все измерения куба равны, то V=АхАхА=А3
Задачи на первичное закрепление материала (слайд 10 - 12)
Ребята, скажите, можно ли применить изученную формулу нахождения объема камня или болта? А вот на этот вопрос нам поможет ответить учитель физики.
По подсказкам, отгадайте:
ü Имя известного учёного, который определил объём тела неправильной формы (слайд 13).
ü Он один из первых учёных, работавших на войну, и первая жертва войны среди людей науки (слайд 14)
ü Он крупный изобретатель. Круг его научных интересов: математика, механика, оптика, астрономия (слайд 15).
ü По легенде, ему принадлежит возглас «Эврика!», прозвучавший вслед за сделанным им открытием (слайд 16)
Архимед (слайд 17)
Как определил Архимед объём тела?
Давайте вспомним легенду об Архимеде.
Существует легенда о том, как Архимед пришёл к открытию, что выталкивающая сила равна весу жидкости в объёме тела. Он размышлял над задачей, заданной ему сиракузским царём Гиероном (250 лет до н.э).
Царь Гиерон поручил ему проверить честность мастера, изготовившего золотую корону. Хотя корона весила столько, сколько было отпущено на неё золота, царь заподозрил, что она изготовлена из сплава золота с другими, более дешёвыми металлами. Архимеду было поручено узнать, не ломая короны, есть ли в ней примесь.
Достоверно неизвестно, каким методом пользовался Архимед, но можно предположить следующее. Сначала он нашёл, что кусок чистого золота в 19,3 раза тяжелее такого же объёма воды. Иначе говоря, плотность золота в 19,3 раза больше плотности воды.
Архимеду надо было найти плотность вещества короны. Если эта плотность оказалась бы больше плотности воды не в 19,3 раза, а в меньшее число раз, значит, корона была изготовлена не из чистого золота.
Взвесить корону было легко, но как найти её объём? Вот что затрудняло Архимеда, ведь корона была очень сложной формы. Много дней мучила Архимеда эта задача. И вот однажды, когда он, находясь в бане, погрузился в наполненную водой ванну, его внезапно осенила мысль, давшая решение задачи. Ликующий и возбуждённый своим открытием, Архимед воскликнул: «Эврика! Эврика!», что значит: «Нашёл! Нашёл!».
Архимед взвесил корону сначала в воздухе, затем в воде. По разнице в весе он рассчитал выталкивающую силу, равную весу воды в объёме короны. Определив затем объём короны, он смог уже вычислить её плотность, а зная плотность, ответить на вопрос царя: нет ли примесей дешёвых металлов в золотой короне?
Легенда говорит, что плотность вещества короны оказалась меньше плотности чистого золота. Тем самым мастер был изобличён в обмане, а наука обогатилась замечательным открытием.
Как это было? (Фрагмент мультфильма « Коля, Оля и Архимед»)
А теперь мы с вами повторим опыт Архимеда
Интерактивная лабораторная работа (отливной сосуд и тело неправильной формы, мензурка) (слайд 19 - 20)
А теперь вы определите объём тела сами опытным путем.
Творческая работа в группах (10 мин)
Оборудование: Измерительный цилиндр (сосуд со шкалой) с водой и деревянный маленький брусок в форме параллелепипеда.
Выполнение работы:
1) Напомнить ученикам, что 1 миллилитр равен 1 кубическому сантиметру.
2) Найти
объем параллелепипеда по формуле ![]() (объем
параллелепипеда равен произведению трех его измерений, то есть длины, ширины и
высоты).
(объем
параллелепипеда равен произведению трех его измерений, то есть длины, ширины и
высоты).
3) Измерить объем воды в измерительном цилиндре.
4) Опустить в сосуд с водой брусок.
5) Измерить теперь объем воды.
6) Вычислить объем вытесненной воды при погружении бруска.
7) Объем вытесненной воды должен совпасть с объемом бруска (1 мл=1 см3).
Сегодня на уроке ученики пятого класса открыли для себя закон Архимеда – один из законов физики.
8) Обозначив объем бруска - V3,объем воды в начале опыта - V1, объем воды с погруженным телом – V2, получим буквенное выражение V3=V2-V1.
Вывод: буквенные выражения - одно из средств, необходимое для определения законов физики.
3. Домашнее задание:
В обычной жизни мы используем такие единицы для измерения объема: мм3, см3, дм3, м3. Какие объемы можно измерить с помощью данных единиц? (Приведите примеры)
4. Подведение итогов:
1) Фронтальный опрос:
ü В каких единицах измеряется объём?
ü Сколько дм3 в 1 л?
ü Как вычислить объём параллелепипеда, куба?
2) Рефлексия:
Предложите фразы, которые ребенок должен закончить.
Например:
- я познакомился с ...
- было непросто ...
- я добился ...
- у меня получилось ...
- хотелось бы ...
- мне запомнилось ...
- я попробую ...
Закончить сегодняшний урок я хотела бы следующими словами.
Дружить наукам можно
вечно,
Вселенная ведь бесконечна!
Спасибо всем вам за урок,
А главное, чтоб был он впрок!
Приложение 2
Форма урока: Интегрированный урок математики и физики в 7 классе
Тип урока: урок систематизации и обобщения знаний и умений.
Тема: «Степень на уроках математики и физики»
Цель урока: Организация условий достижения учащимися образовательных результатов по заданной теме:
· закрепление усвоения информации;
· контроль усвоения информации;
· приобретение новых умений и навыков, применение их на практике;
· формирование УУД (регулятивных, познавательных, коммуникативных).
Задачи урока:
Образовательные:
· способствовать формированию у школьников различных приёмов мыслительной деятельности при выявлении связей физики и математики;
· учить применять свойства степеней при решении физических задач.
Воспитательные:
· привитие интереса к предмету;
· сформировать потребность в знании через показ взаимосвязи между науками и жизнью; через показ значимости математики как метода (языка) научного познания.
Развивающие:
· развивать умение использовать теоретические знания при решении практических задач;
· развивать познавательный интерес к математике и физике;
· расширять кругозор;
Планируемые результаты:
Знать:
Уметь:
Система оценки:
На протяжении всего урока, за каждое задание учащиеся могут набрать определенное количество баллов. Все набранные баллы заносятся в оценочный лист (приложение 4). Критерии оценивания будут озвучиваться перед каждым заданием. Количество набранных баллов «экипажем», озвучивается в конце каждого задания.
Ход урока:
1.Организационный момент. (1 минута)
Здравствуйте, сегодня мы с вами отправляемся в космическое путешествие по физико-математической галактике. Вы разделены на экипажи и каждому экипажу нужно выбрать командира, который назначает отвечающих на вопросы, обеспечивает своевременную сдачу карточек, следит за дисциплиной в группе.
2.Постановка цели урока. (1 минута)
Сегодня мы продолжим работу над степенями. Повторим свойства степеней, а также покажем применение этих свойств при решении физических задач, вспомним этапы решения задач по физике, перевод единиц в систему СИ.
В ходе урока все набранные баллы будут заноситься в оценочный лист. Критерии оценивания будут озвучиваться перед каждым заданием. Перед вами, на столах находятся листы, на которых вы будете производить все вычисления, но итоговое решение вы должны записать в общую карточку.
3.Актуализация опорных знаний и умений учащихся (работа в группах)
Задание1: Найди ошибку (2 минуты письменно + 2 минуты разбор заданий)
- Ученик, выполняя преобразования выражений, допустил ошибки. Исправьте ошибки и объясните, какие определения, свойства и правила не знает ученик. На данное задание вам отводится 2 минуты. По истечении времени один представитель от группы (1 поднявшая руку группа) объясняет решение всех примеров. Если группа отвечает неправильно, то ход переходит к другой группе. За каждый правильно решенный пример, группа получает 1 балл.
5 • 5 • 5 • 5 = 4 5; 2 3 • 2 7 = 4 10;
71 = 1; 2 30 : 2 10 = 2 3;
4 0 = 4; (2х) 3 = 2х 3;
2 3 • 2 7 = 2 21; (а 3) 2 = а 5.
Задание 2: Совершенствование интеллектуальных и практических умений учащихся.
(работа по карточкам 4 минуты+ 1 минута разбор)
Решили задание: теперь проверяем ответы на доске, цветными карандашами вы должны аккуратно зачеркнуть неверное решение и сверху подписать правильное. Те, у кого были ошибки поднимают руки и объясняют в чем была ошибка. Ответственный от группы собирает карточки и сдает учителю на проверку.
4. В этом году вы начали изучать новый предмет- физику. И тут вам не обойтись без математики при подсчетах по физическим формулам.
Задание 3: (1 минута)
Давайте вспомним, какие знания нам могут понадобиться при решении задач по физике. С чего мы начинаем решение задачи?
1) Составить Дано по условию задачи.
2) Необходимо выразить единицы измерения в системе СИ (система единиц физических величин). Перед тем как решить задачу, вспомним, как мы переводим из одной единицы измерения в другую (по группам, задание на экране, группа, которая первая дает правильный ответ получает 1 балл)
(2 минуты)
Ø 72 км/ч=20м/с
Ø 120 км/ч=33м/с
А теперь давайте, переведем единицы измерения в систему СИ, а затем приведем к выражению, содержащему степень.
Ø 8 г =... кг (8*10-3 кг)
Ø 30кН = …Н (3*103Н)
3) Выражение компонентов из формул (2 минуты)
Слайд №7
Задание: Выразить компоненты из формул:
Ø ρ=m/V (плотность)
Ø P=m∙g (вес тела)
Ответ:
Ø m=pV V=m/p
Ø m=P/g. g=P/m (g=9.8 Н/кг)
Итак, мы с вами вспомнили некоторые этапы, которые могут понадобиться при решении физических задач. А теперь давайте решим задачу: (Каждой группе раздается карточка с задачей. На решение задач отводится 3 минуты. В это время у доски оформляет задачу представитель экипажа. По истечении 3-х минут, каждый экипаж сверяет с доской решение задачи и, если есть исправляют ошибки. Оценивается правильное и аккуратное оформление задачи и решение. За правильное решение команда получает 1 балл)
Задача: (3 минуты письменно+ 2 минуты исправление и проверка на доске) приложение 1
№1. Скорость первого искусственного спутника Земли, запущенного в СССР в 1975 г., составляла примерно 28 080 км/ч. Определите путь, пройденный этим спутником за 5 минут (вызываются по одному участнику от команды, первый – составляет дано, второй – переводит в систему СИ, третий – выражает компонент из нужной формулы и решает задачу)
Решение:

№2
За какое время солнечный свет достигает Земли, если расстояние от Земли до Солнца составляет примерно 150∙106 км?

№3
К 17 ч 12 сентября 1959 г. Вторая космическая ракета, доставившая советский вымпел на Луну, удалилась от поверхности Земли на расстояние 101 000 км. К 22 ч того же дня она находилась уже на расстоянии 152 000 км от Земли. Определите среднюю скорость удаления ракеты от Земли.

Молодцы! Без математических навыков вычисления, мы бы не смогли решать задачи по физике.
Задание: (1 минута)
В следующем задании Вам необходимо разгадать кроссворд, в котором зашифровано имя великого древнегреческого ученого математика и физика, ключевое слово – расположено в столбике по вертикали. Сейчас мы проверим ваши знания, полученные на уроках математики и физики. (На столах находятся карточки с кроссвордом, на разгадывание кроссворда отводится 4 минуты, после этого на экране появляются ответы, учащиеся подсчитывают баллы, максимум 7 баллов). Приложение 2
|
1с |
е |
к |
у |
н |
д |
А |
|
|
|||||||||
|
2И |
Н |
Е |
Р |
Ц |
И |
Я |
|
|||||||||
|
3М |
Е |
Х |
А |
Н |
И |
З |
М |
|
||||||||
|
4С |
И |
Л |
А |
|
||||||||||||
|
5М |
Е |
Д |
И |
А |
Н |
А |
||||||||||
|
6С |
Т |
Е |
П |
Е |
Н |
Ь |
|
|
||||||||
|
7Д |
Р |
О |
Б |
Ь |
|
|||||||||||
По горизонтали:
1) Единица времени.
2) Свойство тел сохранять состояние покоя или равномерного прямолинейного движения.
3) Приспособление для преобразования силы.
4) Причина изменения скорости тела.
5) Отрезок в треугольнике, соединяющий вершину треугольника с серединой противолежащей стороной.
6) Выражение, в виде произведения одинаковых множителей, называется….
7) Величина, которая бывает правильной и неправильной.
Вывод: Больше информации, об открытиях Архимеда и других ученых, вы узнаете при дальнейшем изучении алгебры, геометрии и физики. Наш урок является своеобразным “мостиком” между предметами математики и физики.
Теперь вы можете посмотреть на физику и математику совсем другими глазами. А теперь скажите, почему Физика без математики невозможна?
(Математика при изучении физики вооружает нас математическим аппаратом, который прошел через все этапы нашего урока:
ü Вычисления
ü Перевод единиц
ü Выражение компонентов
Подведение итогов урока (рефлексия)
Карточки:
А теперь мы попросим поднять желтую карточку тех, кто уже сталкивался в своей жизни с физико-математическими явлениями (с интеграцией физики и математики)
Те, кому из вас захотелось больше узнать о взаимосвязи между математикой и физикой, поднимите зеленую карточку.
Выставление оценок по «оценочному листу» Приложение 4
Материально – техническое обеспечение:
1. Телевизор (экран + проектор)
2. Презентация
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ 1
Решение задач
№1. Скорость первого искусственного спутника Земли, запущенного в СССР в 1975 г., составляла примерно 28 080 км/ч. Определите путь, пройденный этим спутником за 5 минут.
|
Дано:
|
Си:
|
Решение: |
|
|
Решение задач
№2
За какое время солнечный свет достигает Земли, если расстояние от Земли до Солнца составляет примерно 150∙106 км? (подсказка: скорость света C ≈ 3• 108 м/c)
|
Дано:
|
Си:
|
Решение: |
|
|
Решение задач
№3
К 17 ч 12 сентября 1959 г. Вторая космическая ракета, доставившая советский вымпел на Луну, удалилась от поверхности Земли на расстояние 101 000 км. К 22 ч того же дня она находилась уже на расстоянии 152 000 км от Земли. Определите среднюю скорость удаления ракеты от Земли.
|
Дано:
|
Си:
|
Решение: |
|
|
ПРИЛОЖЕНИЕ 2
Кроссворд
|
1 |
|
|
|
|
|
|
|
|
|||||||
|
2 |
|
|
|
|
|
|
|
|||||||
|
3 |
|
|
|
|
|
|
|
|
||||||
|
4 |
|
|
|
|
||||||||||
|
5 |
|
|
|
|
|
|
||||||||
|
6 |
|
|
|
|
|
|
|
|
||||||
|
7 |
|
|
|
|
|
|
||||||||
По горизонтали:
1) Единица времени.
2) Свойство тел сохранять состояние покоя или равномерного прямолинейного движения.
3) Приспособление для преобразования силы ...
4) Причина изменения скорости тела.
5) Отрезок в треугольнике, соединяющий вершину треугольника с серединой противолежащей стороной.
6) Выражение, в виде произведения одинаковых множителей, называется ….
7) Величина, которая бывает правильной и неправильной.
ПРИЛОЖЕНИЕ 3
Сообщение: Архимед
Несомненно, Архимед — самый гениальный учёный Древней Греции. Он стоит в одном ряду с Ньютоном, Гауссом, Эйлером, Лобачевским и другими величайшими математиками всех времён. Его труды посвящены не только математике. Архимед сделал замечательные открытия в механике, хорошо знал астрономию, оптику, гидравлику и был поистине легендарной личностью. Он проживал с 287-212г до нашей эры. Во время службы у царя Герона II, Архимед определил чистоту состава золотого венца царя при помощи найденного им закона выталкивающей силы, тогда он воскликнул «ЭВРИКА», что означало - нашел.
Хорошо известен рассказ о жертвенном венце Герона. Архимеду поручили проверить честность ювелира и определить, сделан венец из чистого золота или с примесями других металлов и нет ли внутри него пустот. Однажды, размышляя об этом, Архимед погрузился в ванну, и заметил, что вытесненная его телом вода пролилась через край. Гениального учёного тут же осенила яркая идея, и с криком “Эврика, эврика!” он, как был нагой, бросился проводить эксперимент. Идея Архимеда очень проста. Тело, погружённое в воду, вытесняет столько жидкости, каков объём самого тела. Поместив венец в цилиндрический сосуд с водой, можно определить, какое количество жидкости он вытеснит, т.е. узнать его объём. А, зная объём и взвесив венец, легко вычислить удельную массу. Это и даст возможность установить истину: ведь золото — очень тяжёлый металл, а более лёгкие примеси, и тем более пустоты, уменьшают удельную массу изделия. Но Архимед на этом не остановился. В труде “О плавающих телах” он сформулировал закон.
Другая легенда рассказывает, что Архимед соорудил систему блоков, с помощью которой один человек смог спустить на воду огромный корабль. Крылатыми стали тогда произнесенные Архимедом слова: «Дайте мне точку опоры, и я поверну Землю»
Его конструкторские способности использовались в военных целях при защите стен города. Огромен вклад Архимеда и в развитие математики. Ученый вычислил отношение длины окружности к диаметру. Используя принцип интегрирования, Архимед открыл число пи.
ПРИЛОЖЕНИЕ 4
Оценочный лист
|
Задания |
1 экипаж |
2 экипаж |
3 экипаж |
|
Найди ошибку |
|
|
|
|
Работа по карточкам |
|
|
|
|
Перевод в систему СИ (1 балл за каждый прав. ответ) |
|
|
|
|
Выражение компонентов из формул (1 балл за каждый прав. ответ) |
|
|
|
|
Решение задачи (1 балл за каждый прав. ответ) |
|
|
|
|
Кроссворд (1 балл за каждый прав. ответ) |
|
|
|
|
ИТОГО: |
|
|
|
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.