Использование эвристических приёмов при решении задач

1.     Докажите, что число состоящее из 243 единиц, делится на 243.

Решение. Заметим, что 243 = 3⁵ . Попробуем доказать более общее утверждение, что число, составленное из 3ⁿ единиц, делится на 3ⁿ. Оказывается, это проще.

Для n = 1 утверждение верно (111 делится на 3).

Заметим, что 111111111 = 111 · 1001001, и вообще число из 3ⁿ единиц разлагается на множители:

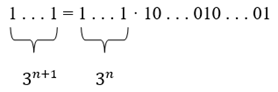
причём, второй множитель делится на 3 (по признаку делимости на 3). Итак, в последовательности чисел 111, 111111111, . . . , «3ⁿ единиц» каждое следующее равно предыдущему, умноженному на число, кратное трём. Поэтому, если
1 . . . 1 делится на 3ⁿ⁻¹ , то 1 . . . 1  делится на 3ⁿ.

Теперь индукция очевидна.

2.     Представить выражение (а+b)² в виде суммы слагаемых.

Решение: Рассмотрим квадрат со стороной (a+b). Разобьем его стороны на отрезки a и b, как показано на рисунке.

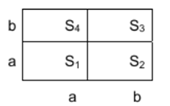
Тогда площадь квадрата будет равна сумме площадей двух квадратов и двух прямоугольников.

(а+b)² = (а+b)(а+b) = S₁ + S₂ +S₃ + S₄ = a² + ab + b² + ab = a² + 2ab + b²

3.     В классе 16 учащихся, среди них два друга — Олег и Вадим. Класс случайным образом разбивают на 4 равные группы. Найдите вероятность того, что Олег и Вадим окажутся в одной группе.

Решение. Пусть один из друзей находится в некоторой группе. Вместе с ним в группе окажутся 3 человека из 15 оставшихся одноклассников. Вероятность того, что второй друг окажется среди этих 3 человек, равна 3 : 15 = 0,2.

Ответ: 0,2.

Переформулируем задачу так, чтобы приведенное решение стало более понятным.

Задача. В классе 16 учащихся, среди них два друга — Олег и Вадим. Класс случайным образом разбивают на 4 равные группы. Олег попал в одну из групп. Найдите вероятность того, что Вадим окажется в той же группе.

Решение: Места в четырех группах могли разыгрывать с помощью урны — ребята тянули по очереди жребий — бумажки с номерами групп. Не нарушая общности, можно считать, что первым тянул жребий Олег, а вторым Вадим. Тогда у Вадима было 3 возможности из 15-ти попасть в группу Олега.