Использование информационного блока в дистанционном изучении математики

Использование информационного блока в дистанционном обучении по математике

Т.Н. Масанина,  методист

АУ «Сургутский политехнический колледж»

Дистанционное обучение (ДО) - новая организация образовательного процесса, базирующаяся на принципе самостоятельного обучения учащегося. Среда обучения характеризуется тем, что учащиеся в основном, а часто и совсем, отдалены от преподавателя в пространстве и (или) во времени, в то же время они имеют возможность в любой момент поддерживать диалог с помощью средств телекоммуникации.

Цель дистанционного урока: освоение учебных программ с использованием дистанционных технологий, с целью формирования у учащихся навыков творческого, критического мышления, самостоятельности в организации и регулировании собственной деятельности, развитии уровня ИКТ-компетентности. В процессе обучения учащийся приобретает навык самостоятельного проектирования индивидуальной образовательной стратегии.

Задачи:

·         формировать у учащихся навык эффективного поиска и отбора информации, ее структурирования, анализа и оценки;

·         давать оценку информации с точки зрения ее дидактических свойств: достоверности, полноты, ценности, актуальности, динамичности (или статичности);

·         формирование навыков самооценивания, сравнения получаемых в автоматическом режиме результатов с прогнозируемыми;

·         осуществление самокоррекции своей учебной деятельности, развитие навыка рефлексии модернизировать формы педагогического контроля в условиях применения новых средств обучения: сетевых учебных курсов, интерактивных обучающих компьютерных программ, тренажеров, тестов;

·         освоения учащимся новых видов деятельности: работа в тестовом режиме,

·         интерактивный (онлайн) режим.

На мой взгляд, большое внимание при подготовке к дистанционному обучению играет информационный блок. Информация к учащимся поступает через экран компьютера, т.е. основным каналом информации является визуальный. Поэтому материал должен выглядеть привлекательно, быть читаемым и не раздражающим глаз. Учитывая уровень подготовки учащихся и их учебные навыки, информация должна быть доступна для понимания и восприятия учебного материала

Рассмотрим информационный блок по математике для учащихся первого курса, обучающихся по программам подготовки квалифицированных рабочих социально-экономического направления.

Тема: Определение первообразной

Прочитать по учебнику  «Алгебра и начала анализа 10-11» п.54 и ответить на вопросы:

1.      Какая функция называется первообразной.

2.      Какой буквой обозначается первообразная.

3.      Сколько первообразных имеет функция и как они обозначаются.

4.   Рассмотрите таблицу 1. В первой колонке находится  ,  а в соседней колонке её первообразная.

5.      Решить №983,984,985

6.      Образцы решения№983,984:

1.   Показать, что функция  является первообразной для функции  на всей числовой прямой.

,          

 По определению первообразной должно выполняться условие:  .

Проверим это условие:

 .

2.      Образец решения №985.

 Найти все первообразные функций:

. Воспользуемся таблицей, формулой №2. Вместо n подставляем число 15 и смотрим в соседнюю колонку и находим первообразную.  То есть

Таблица 1

Тема:  Правила вычисления первообразной

Прочитать по учебнику  «Алгебра и начала анализа 10-11» п.55, решить № 988, 989, 992

Правило 1

Если f(x) имеет – первообразную F(x), а g(x) имеет первообразную G(x), то f(x)+g(x)имеет первообразную F(x)+ G(x)+С

Первообразная суммы равна сумме первообразных

Правило 2

Если функция f(x)– имеет первообразную F(x), а  k –константа, то   kf(x) имеет первообразную kF(x)+С

Постоянный множитель можно выносить за знак первообразной

Правило 3

Если функция  f(x) имеет – первообразную F(x), то функция , где ,  постоянные числа, то  она имеет первообразную: .

Чтобы проще было пользоваться правилом 3 и для закрепления навыков, можно воспользоваться таблицей

Таблица 2

1.   Найти первообразную функции , воспользуемся таблицей 2 (строка 15)

        Решение:  +С.

2.      Найти первообразную функции , воспользуемся таблицей 2 (строка 15)

Решение:

3.      Найти первообразную функции    , воспользуемся таблицей 2 (строка 17)

       Решение:   

4.   Найти первообразную для функции  

      Решение:  Используем правила 1,2,3.

Тема: Площадь криволинейной трапеции

Прочитать п.56  по учебнику «Алгебра и начала анализа 10-11»

Выполнить задания №1000.

Пояснения к заданию:

Построим в системе координат прямые

Обращаю ваше внимание, что

 не точки,  а прямые.

 – это прямая, проходящая через точку  на оси (ох) и параллельно оси (оу). (Смотрите на рисунок)

  – это прямая, проходящая через точку  на оси (ох) и параллельно оси (оу).

 .

Определение. Криволинейной трапецией  называется фигура, ограниченная прямыми

 и непрерывной положительной функцией 

Криволинейная трапеция имеет площадь, которая вычисляется по следующему алгоритму;

1.   Находим первообразную      

2.   Находи значение первообразной в точке  

3.   Находи значение первообразной в точке  

4.      Находим разность. Это и есть искомая площадь

Образец решения примеров

Найти площадь фигуры, ограниченной гиперболой ,  прямыми  

Сначала делаем рисунок. Находим несколько значений для гиперболы. Обязательно берем

значения   и еще несколько точек, чтобы более точно построить график. Например

Находим значение функций:

;    ;     

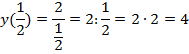
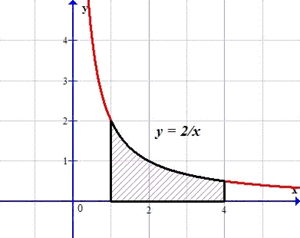Расставляем эти точки в системе координат  и строим график гиперболы. Проводим прямые

 и получаем рисунок

Используя  алгоритм, вычисляем площадь.  Функцию  ,  преобразуем и запишем в виде: , 

1.     Находим первообразную   по второму правилу и по таблице(строка 10):

. Обращаю внимание, что при нахождении площадей +С не пишем.

2.    Находи значение первообразной в точке   

3.    Находи значение первообразной в точке   

4.       Находим разность. Это и есть искомая площадь

Напоминаю:

·         разность логарифмов заменяем частным;

·         так как вычисляли площадь,  а площадь измеряется в квадратных единицах, то дописываем  .

Дистанционное образование, несомненно, имеет свои преимущества перед традиционными формами обучения. Оно решает психологические проблемы учащегося, снимает временные и пространственные ограничения, проблемы удалённости от квалифицированных учебных заведений, помогает учиться людям с физическими недостатками, имеющими индивидуальные черты и неординарные особенности, расширяет коммуникативную сферу учеников и педагогов.