Использование кейс-технологии на занятиях математики в СПО

Использование кейс-технологии на занятиях математики в СПО

Почтарькова Татьяна Петровна, преподаватель

ФГБОУ ВО Мичуринский ГАУ  Центр-колледж прикладных квалификаций

г.Мичуринск, Тамбовской обл.

На современном этапе развития общества повышаются требования к профессиональному уровню специалистов, к сокращению сроков внедрения последних достижений науки и прогрессивных технологий в производственную и социальную сферы. Исходя из этого, меняются цели и задачи, стоящие перед современным образованием. Акцент переносится с «усвоения знаний» на формирование «компетентности», происходит переориентация на личностно-ориентированный подход.

Какие условия для этого необходимы? Прежде всего, возможность вовлечения каждого обучающегося в активный познавательный процесс, причем не процесс пассивного овладения знаниями, а активной познавательной деятельности, применения им на практике этих знаний и четкого осознания где, каким образом и для каких целей эти знания могут быть применены.

Поставив своей целью научить обучающихся самостоятельно мыслить, принимать решения, работать в группах, брать на себя ответственность, преподаватели всех уровней образования изучают и применяют инновационные методы в обучении, среди которых особое место занимает кейс - метод.

Кейс-метод часто называют методом анализа конкретных ситуаций. Суть этого метода состоит в следующем: в процессе обучения используется описание какой-либо реальной (или вымышленной) ситуации, содержащей конкретную практическую проблему. Обучающимся необходимо проанализировать предложенную ситуацию и определить возможные пути её решения. При этом поставленная проблема не всегда может иметь однозначное решение. При использовании кейс - технологии обучающиеся, опираясь на собственный опыт, учатся формулировать выводы, применять на практике полученные знания, предлагать собственный (или групповой) взгляд на проблему. Результаты выполненных кейсов должны быть конкретными и обоснованными, такими, чтобы их можно было использовать на занятии или в реальной жизни.

Кейс-технология сочетает в себе исследовательские, поисковые и проблемные методы, способствует развитию творческих способностей участников образовательного процесса. Кроме того, обеспечивает индивидуальный подход к каждому обучающемуся, свободу в обучении и возможность выбора.

Условно все кейсы можно разделить на практические, обучающие и научно-исследовательские.

При разработке заданий для обучающего кейса по математике необходимо выделить проблемную ситуацию, решение которой базируется на теоретическом материале, находящемся в зоне актуального развития обучающегося, но при этом представляющем для него некоторую новизну (по постановке задачи, по способу решения и т. п.) [1,с.57]. При этом задача в обучающем кейсе может разделяться педагогом на несколько подзадач, решение которых позволит учащемуся приблизиться к решению главной задачи, проясняя для него данную ситуацию, помогая ее анализировать.

Задания для исследовательского кейса характеризуются более высоким уровнем сложности. Однако их содержание, методы и способы решения должны находиться в зоне ближайшего развития обучающегося. Задания для исследовательского кейса требуют для своего решения изучения дополнительного материала, содержащего новую информацию для обучающегося, или привлечения теоретических знаний  и практических умений из различных разделов математики и других познавательных областей. В качестве примера заданий для исследовательского кейса можно рассматривать содержательные олимпиадные задачи.

Задания для практического кейса по математике чаще всего предполагают индивидуальную работу обучающихся. Их можно рассматривать непосредственно на занятии или предлагать решение на дом, если они предполагают определённые временные затраты. Проверка решения таких заданий не характеризуется особой сложностью. Она может проводиться разными способами: с помощью фронтального обсуждения решения с учениками с выявлением алгоритма действий и проверкой промежуточных ответов; путём обсуждения обучающимися полученных индивидуальных решений задания в малых группах, с дальнейшим итоговым выступлением «спикера» группы перед всей аудиторией.

Рассмотрим несколько примеров кейсов, которые могут быть предложены обучающимся на 1 курсе.

1. Завод сельхозмашин в 2018 году выпустил некоторое количество тракторов, а комбайнов на 10000 штук меньше, чем тракторов. В 2019 году некоторые виды работ были автоматизированы, поэтому выпуск тракторов увеличился на 14%, а комбайнов на 25%, и общее количество выпускаемых машин увеличилось на 5300. На реконструкцию было израсходовано 300 млн. рублей. Определить, на сколько увеличилась годовая прибыль после реконструкции, если себестоимость тракторов и комбайнов снизилась с 6 млн. рублей до 5,25 млн. рублей, а завод их реализует предприятиям по 8,25 млн. рублей?

2. Пусть у вас есть 100000 рублей и вы хотите сделать из них миллион. Предположим, что вы делаете стабильно в месяц 10 %. Сколько лет уйдет, пока вы достигнете цели?

3. В начале 2020 года у Алексея было 100000 рублей. Он может на них приобрести  ценные бумаги по цене 25000 рублей каждая или положить деньги на счёт в банке. В конце каждого года цена каждой бумаги возрастает на 3000 рублей. Каждый год сумма на счёте будет увеличиваться на 10%. В начале любого года Алексей может продать бумагу и положить вырученные деньги на банковский счет и наоборот снять деньги со счёта и приобрести на них ценные бумаги. Как должен распорядиться Алексей своим капиталом, чтобы через 10 лет иметь с него наибольшую прибыль?

4. У фермера есть два поля, каждое площадью 10 га. На каждом поле можно выращивать картофель и свеклу, поле можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 300 ц/га, а на втором – 200 ц/га. Урожайность свеклы на первом поле составляет 200 ц/га, а на втором – 300 ц/га. Фермер может продавать картофель по цене 4000 рублей за центнер, а свеклу – по 5000 рублей за центнер. Какой наибольший доход может получить фермер?

Приведу также ряд примеров кейсов, используемых мною на занятиях по математическим дисциплинам, изучаемых студентами 2 и 3 курсов специальности 09.02.02 Компьютерные сети:

1. Проведите эксперимент: подбросьте игральный кубик 30 раз и запишите число очков, выпавших на его грани. Запишите вариационный ряд. Постройте статистический ряд случайной величины Х – числа очков. Найдите: размах вариации R; моду M0; медиану Me; выборочное среднее ; выборочную среднюю дисперсию Db; выборочное среднеквадратическое отклонение σb.  Запишите закон распределения случайной величины Х – числа очков, выпавших на грани кубика. Найдите математическое ожидание и среднеквадратическое отклонение этой величины. Сравните вероятностные и статистические числовые характеристики случайной величины Х. Сделайте вывод. Повторить эксперимент, выполнив 100 подбрасываний кубика. Сравните результаты. Сделайте вывод.

2. Проведите эксперимент: подбросьте монету 5 раз и запишите число появлений «орла». Повторите ещё 9 раз. Запишите результаты эксперимента. Запишите вариационный ряд. Постройте статистический ряд случайной величины Х – числа выпадений «орла». Найдите: размах вариации R; моду M0; медиану Me; выборочное среднее ; выборочную среднюю дисперсию Db; выборочное среднеквадратическое отклонение σb. Запишите закон распределения случайной величины Х – числа выпадений «орла» в результате 5 подбрасываний монеты. Найдите математическое ожидание и среднеквадратическое отклонение этой величины. Сравните вероятностные и статистические числовые характеристики случайной величины Х. Сделайте вывод. Повторите эксперимент, выполнив 100 раз по 5 подбрасываний монеты. Сравните результаты. Сделайте вывод.

3. Имеется 5 точек доступа. Наличие прямых связей между ними описывает бинарное отношение Р={(1,2), (1,3), (1,5), (2,1), (2,3), (2,4), (3,2), (4,3), (4,5), (5,1), (5,4)}. Нарисовать на плоскости граф G(M,P), соответствующий бинарному отношению Р. Найти матрицу смежности А и матрицу инцидентности В графа G. Определить существование (3, 5) маршрута и его длину. Найти матрицу связности. Составить матрицу расстояний. Найти диаметр, радиус, центральные и периферийные вершины.

4. Компьютерная сеть организации задана взвешенным графом.

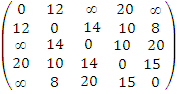
Начертите граф. Найдите:  Остов минимального веса. Все кратчайшие маршруты из вершины 1 до всех остальных вершин графа. Матрицу расстояний (вершина-вершина) графа. Внешний и внутренний центр. Внешнюю и внутреннюю медиану. Определите, в какой из вершин графа оптимально было бы расположение сервера.

5. В центре информационных технологий ремонтом компьютеров занимаются 4 мастера. В среднем в течение дня поступает в ремонт 9 компьютеров. Каждый из мастеров за смену ремонтирует в среднем 3 компьютера. Требуется определить: а) вероятность того, что все мастера свободны от ремонта компьютеров; б) вероятность того, что все мастера заняты ремонтом; в) среднюю длину очереди; г) среднее время ожидания начала ремонта для каждого компьютера; д) среднее время ремонта одного компьютера; е) среднее число мастеров, занятых ремонтом.  Определите оптимальное число мастеров в центре, если условием оптимальности считать удовлетворение из каждых 100 заявок в среднем не менее 90 заявок и средняя длина очереди не превышает 0,2 заявок.

В последнее время кейсы широко используются в материалах ОГЭ, ЕГЭ по математике и Интернет-экзаменов по математическим дисциплинам, проводимых ФИРО. Решение такого типа заданий показывает высокий уровень обученности обучающихся.

Но не менее важно то, что метод кейс-стади позволяет обучающимся проявлять инициативу и самостоятельность в освоении теоретических вопросов учебной дисциплины и в овладении практическими навыками, использовать межпредметные связи; а анализ конкретных ситуаций способствует их взрослению, расширяет кругозор, формирует, поддерживает интерес и позитивную мотивацию к учебной деятельности [3].

И самое главное, кейс-метод меняет мышление преподавателя, даёт возможность творчески и разносторонне планировать свою деятельность, создавать новый дидактический материал, объединяющий различные разделы учебной дисциплины, а также связывающий различные дисциплины между собой и реальной жизнью.

Литература:

1. Винеская, А. В. Метод кейсов в педагогике: практикум для учителей и студентов. — Ростов-на-Дону: Феникс, 2015. — 141 с.

2. Сурмин, Ю., Сидоренко А., Лобода В. Ситуационный анализ, или Анатомия Кейс-метода. — Киев: Центр инноваций и развития, 2002. — 286 с.

3. Устинова, Т. Б. Кейс-технологии как условие активизации самостоятельной работы студентов колледжа [Электронный ресурс]. URL: festival. 1september. ru/articles/512028/.