Использование на уроках математики опорных схем, зачётов.

  Использование  на уроках математики опорных схем, зачётов.

(из опыта работы учителя математики МКОУ СОШ с.Скворчиха

МР Ишимбайский район РБ Осиповой Л.А.)

Актуальность идеи: 

        наглядность, компактность записей- конспектов,

        создание ситуации успеха в учебе,

        выработать навыки  выполнять схемы и умения их читать,

    развивать внимательность, умение сравнивать, умение пользоваться формулами,

        навыки работы индивидуальные и  в группе.

 Назначение опорного конспекта заключается в следующем:

       наглядное представление учебного материала в целом и по частям;

       понимание структуры изучаемого материала;

       выделение главного в излагаемом материале;

       комплексное представление изучаемого материала при его повторении;

       развитие творческих способностей.

   Учебные способности обучающихся зависят от нескольких факторов, наиболее сильным из которых являются интеллектуальные способности. Основная задача учителя - воспитать  мыслящую личность. Учитель должен  организовать  учебный процесс путем целенаправленного развития предметно-речевых навыков и предметного понятийного аппарата, включающий в себя  толкование понятий.

   В основе формирования понятийного аппарата лежат навыки работы с текстом - чтение и письмо. Основным источником информации в учебной деятельности школьников является учебник.

   На протяжении нескольких лет я использую на уроках технологию организации и проведения школьных лекций, семинаров и зачетов.  Ключевые моменты, примеры, опорные схемы и отдельные фразы ребята выделяют  рамками, подчеркиваниями, схемами.

Многие опорные фразы, слова и схемы ввела  сама, например:

- при отработке формул сокращенного умножения использовала выражения Ӏ и ӀӀ  :  

1. ( Ӏ + ӀӀ)² =(Ӏ)² + 2(Ӏ)*( ӀӀ) + (ӀӀ )²

2. (Ӏ – ӀӀ)² = (Ӏ)² – 2(Ӏ) * ( ӀӀ) + (ӀӀ )²

3. (Ӏ)² – (ӀӀ )² = (Ӏ – ӀӀ) * (Ӏ + ӀӀ)

4. (Ӏ)³ + (ӀӀ )³ = (Ӏ + ӀӀ) * ((Ӏ)² – Ӏ* ӀӀ + (ӀӀ )²)

5. (Ӏ)³ – (ӀӀ )³ = (Ӏ – ӀӀ) * ((Ӏ)² + Ӏ* ӀӀ + (ӀӀ )²)

6.(Ӏ + ӀӀ)³ = (Ӏ)³ + 3(Ӏ)² *(ӀӀ ) + 3(Ӏ) *( ӀӀ )² + (ӀӀ )³

7.(Ӏ – ӀӀ)³ = (Ӏ)³ – 3(Ӏ)² *( ӀӀ) + 3(Ӏ) *( ӀӀ )² – (ӀӀ )³.

   Так как  при использовании формулы квадрата суммы двух выражений : ( а+в)²= а² + 2ав + в²  наиболее часто встречающимися ошибками обучающихся являются, например:

( 4х + 3у)² = 4х² + 24ху + 3у², так как некоторые обучающиеся думают, что надо в квадрат возводить только переменные. При использовании формулы 1, такого не происходит, так как в квадрате стоят целиком первое выражение  и в квадрате целиком второе выражение.

   Так как формулы 1-7 являются тождествами, то верны они и справа налево и используются  при разложении  многочлена на множители.

 1*. (Ӏ)² + 2(Ӏ)*( ӀӀ) + (ӀӀ )²= ( Ӏ + ӀӀ)²

 2*. (Ӏ)² – 2(Ӏ) * ( ӀӀ) + (ӀӀ )²= (Ӏ – ӀӀ)² и т.д.

  Типичными ошибками при разложении на множители по формуле  а² + 2ав + в² =( а+в)² являются, у некоторых обучающихся, например: 4х² + 24ху + 9у² = (4х + 9у)², а при использовании формулы 1* видно, что надо вначале выделить целиком квадрат первого выражения, затем выделить удвоенное произведение первого выражения на второе и выделить целиком квадрат второго выражения, то только тогда представляем квадрат суммы первого и второго выражений.

-  при применении формулы  ( √¯а)² =|а|   «квадрат и корень исчезает»,

-  при решении уравнении х² =а  «квадрат исчезает, ± корень появляется»,

-  слово единственный заменяю значком !

-  слово существует заменяю значком     и т.д.        

    На уроках опорные схемы помогают запоминать теорию,  при решении  задач используются. Такая система позволяет избежать множества ошибок, повторяющихся из года в год.  К созданию опорных схем привлекаются и сами учащиеся. Так, например, ребятами были предложены следующие схемы:

  - при превращении смешанного числа в неправильную дробь:

- нахождение неизвестного компонента при решении уравнений  в 5 классе:

- при умножении многочлена на многочлен применение опорной схемы «стрелочки»:

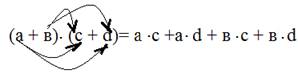и т.д.

  Опорные схемы используются активно на уроках геометрии при изучении теоретического материала. Например, в 7 классе  при изучении главы « Треугольники.»

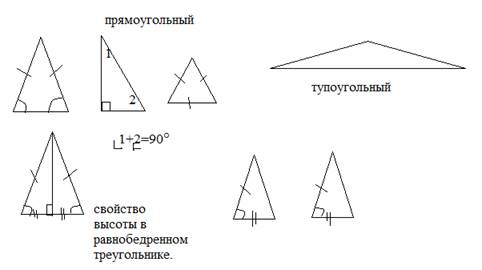    и т.д.

  Опорные схемы и фразы  не мешают овладению языком науки, а, наоборот, помогают в запоминании соответствующих правил и законов математики. Выбор различных способов конспектирования :опорные схемы, таблицы способствуют не только лучшему запоминанию основ теоретического материала, но и быстро находить его.

     Следующий этап  - это зачёт по теории. Практикую различные виды зачётов :

- карточные зачёты,

- опрос «цепочкой»,

- тестирование .

   Семинары чередуются с самостоятельными и проверочными работами различного типа, тестами, математическими диктантами, причём при проведении самостоятельных работ обучающегося характера разрешаю пользоваться  тетрадями для формул, схем. Ребята, не успевшие решить все задания, берут карточки на дом или продолжают выполнять задания после уроков. Цель таких занятий - максимально ликвидировать пробелы в знаниях одних обучающихся  и повысить уровень  подготовки других.  В течении урока и в конце  обращаю внимание на типичные ошибки. Поэтому последний урок по теме - это не только урок работы над ошибками, но и обсуждение дополнительного материала по предмету.

     Пример заданий  теоретического зачёта по геометрии в 7 классе по теме « Соотношения между сторонами и углами треугольника».

Верно ли, что:

    1.Сумма углов тупоугольного треугольника равна 180  ̊.

    2. В любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или

        прямой.

     3. Треугольник является прямоугольным и равнобедренным, если угол при основании прямой.

     4. Если один из углов треугольника тупой, то треугольник называется тупоугольным.

     5. Сторона прямоугольного треугольника, лежащая напротив прямого угла, называется катетом.

     6. В треугольнике против большего угла лежит большая сторона.

     7. Каждая сторона треугольника больше суммы двух других сторон.

     8. Для любых трех точек А, В и С верно неравенство: АВ< АС+СВ

     9. Перпендикуляр, проведенный из точки к прямой, больше любой наклонной, проведенной из

         этой же точки к этой  прямой.

    10. Прямоугольные треугольники могут быть равны по двум катетам.

Отвечать: да или нет.

     Используя такую методическую работу к окончанию школы у ребят сформируются умения конспектировать учебный материал, работы с учебником и дополнительной литературой,  выработаются навыки самостоятельной работы . Чёткая система мобилизует обучающихся на усвоение математики в школе .