ИСПОЛЬЗОВАНИЕ ПРОГРАММЫ EXCEL ДЛЯ ВЫПОЛНЕНИЯ ЗАДАНИЙ ЕГЭ

ИСПОЛЬЗОВАНИЕ ПРОГРАММЫ EXCEL ДЛЯ ВЫПОЛНЕНИЯ ЗАДАНИЙ ЕГЭ

Кузнецова Ирина Васильевна,

учитель предмета «Информатика и ИКТ» МОУ «Специализированная школа №35 г. Донецка», г. Донецк, ДНР

Аннотация: В данной статье автор рассматривает особенности выполнения заданий ЕГЭ по предмету «Информатика и ИКТ» в 2021 году в программе Excel.

Ключевые слова: ЕГЭ, подготовка к экзамену, Excel, функции, динамическое программирование.

Каждый человек независимо от профессии в течение своей жизни постоянно встречается с таблицами, в которых данные представляются в структурированном виде. Например, классный журнал в школе, дневник ученика, табель уровня достижений, расписание уроков, работы кружка или спортивной секции, бюджет семьи, перечень книг в библиотеке, перечень товаров на складе, начисления заработной платы, расписание движения автобусов, поездов или самолетов.

Табличное представление данных позволяет легче воспринимать данные при необходимости их обрабатывать. В таблицах могут содержаться как числовые, текстовые, так и графические данные. В зависимости от типа данных, а также от потребностей их можно по-разному обрабатывать: дополнять, упорядочивать по различным признакам, подбирать, объединять и группировать, выполнять вычисления, представлять графически. При этом для упрощения и ускорения такой работы в случае большого количества данных или сложности их обработки можно использовать различные средства, в том числе компьютер.

Упростить процесс создания и обработки таблиц можно при помощи табличного процессора. Он позволяет автоматизировать вычисления, поиск и отбор данных, а также наглядно представлять данные в виде диаграмм.

В пакет программ Microsoft Office входит табличный процессор MS Excel. Эта программа помогает решать значительное количество задач, которые могут возникать при обработке числовых данных от решения обычных задач по математике до ведения бюджета семьи, построения диаграмм проведенного социального исследования, прогнозирования курса валют и уровня инфляции, вычисление процентов от вкладов в банке.

Рассмотрим типы задач, предложенные для решения в ЕГЭ 2021. Согласно Кодификатору, все они проверяют навыки использования инструментов решения статистических и расчётно-графических задач.[4]

Тема 1. Функции в электронных таблицах

Это задание проверяет умения обрабатывать числовую информацию в электронных таблицах.[5] Для вычисления максимального, минимального и среднего арифметического значений диапазона (например, A1:G20) используются соответственно функции

МАКС(A1:G20),

МИН(A1:G20),

СРЗНАЧ(A1:G20).

В списке аргументов этих функций можно указывать несколько диапазонов и адресов ячеек, разделив их точкой с запятой, например:

МАКС(A1:G20;H15;K12:Y90),

МИН(A1:G20;H15;K12:Y90),

СРЗНАЧ(A1:G20;H15;K12:Y90).

Все три функции игнорируют пустые ячейки и ячейки, содержащие нечисловые данные.

Пример задания: Откройте файл электронной таблицы, содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Найдите разность между максимальным значением температуры и её минимальным значением. В ответе запишите только целую часть получившегося числа.[3]

Решение:

Откроем электронную таблицу. Нужно определиться с диапазоном значений и записать формулу =МАКС(B2:Y92)-СРЗНАЧ(B2:Y92) в пустую ячейку, в данном случае очень удобно выбрать ячейку А1.

После ввода формулы получаем значение 14.3, из которого нужно выделить целую часть, а не округлить, например для значения 14,9 ответ также будет 14.

Ответ: 14.

Тема 2. Динамическое программирование.

Решение этого задания проверяет умение обрабатывать вещественные выражения в электронных таблицах. [5]

В задачах этого типа нужно найти оптимальный путь для Робота, который перемещается на клетчатом поле. Робот может на каждом шаге выбирать одно из двух направлений движения (например, только вправо и вниз).

В каждой клетке Робот «берёт монету», и нужно найти такой путь, при котором общая награда будет наибольшая (или наименьшая). Эта задача успешно и быстро решается с помощью динамического программирования – метода оптимизации, который предложил американский математик Ричард Беллман. Он сформулировал очень простой принцип оптимальности пути: любая часть оптимального пути оптимальна. Например, пусть мы нашли оптимальный путь из точки А и точку Б, который проходит через точки В, Г и Д:

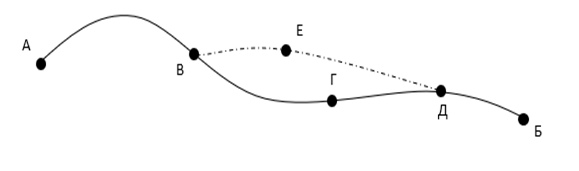
Рис. 1. Оптимальный путь

Принцип Беллмана утверждает, что, например, путь ВГД – это оптимальный путь из В в Д. Если бы это было не так и существовал бы другой, лучший путь между В и Д (например, ВЕД на рисунке), то и путь АВГДБ не был бы оптимальным.

Пример задания: Исходные данные записаны в файле в виде электронной таблицы прямоугольной формы. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой НИЖНЕЙ клетки в правую ВЕРХНЮЮ. В ответе укажите два числа – сначала максимальную сумму, затем минимальную.[3]

Решение:

Откроем электронную таблицу и увидим следующую таблицу размером 10 на 10. Робот начинает движение из верхнего левого угла (А1) и перемещается в правый нижний (J10). При использовании метода динамического программирования требуется выделить для вычислений дополнительную таблицу такого же размера. Для этого нужно скопировать исходную таблицу вниз и обвести её рамкой, чтобы запомнить исходный размер, стереть все данные в копии.

Дальше будем работать только с полученной областью. Предположим, что робот уже находится в правом нижнем углу. В этом случае он может получить только сумму в этой ячейке, то есть величину J10; записываем в J22 формулу =J10. После ввода формулы видим в ячейке J22 значение 33.

Рассмотрим нижний ряд: если Робот находится в одной из ячеек последней строки 10, то он может идти только вправо, собирая монеты в последней строке; например, начав движение из ячейки I10 он соберёт монету в этой ячейке и во всех следующих, то есть формула в ячейке I22 должна быть =I10+J22;

Первая ссылка в формуле (I10) обращается к исходной таблице (берёт из неё одно значение), а вторая (J22) – к рабочей (берёт всё накопленное далее), в I22 появляется число 73. Эту формулу копируем по всей строке 22.

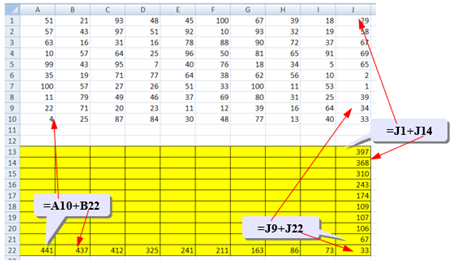
Рис. 2. Поиск оптимального пути на границах диапазона

Аналогично если Робот находится в последнем столбце, он может двигаться только вниз, собирая по пути все монеты; вводим в ячейку J21 формулу =J9+J22 и копируем её вверх на весь столбец J вспомогательной таблицы.

Пусть Робот находится в ячейке I9; тогда для того, чтобы получить максимальную сумму, ему нужно выбрать лучший из двух путей – пойти в I10 или в J9; из второй таблицы видим, что в первом случае дополнительно к значению I9 он получит сумму 73, а во втором – только 67, поэтому выгоднее первый вариант. В формуле нужно выбрать максимум из значений ячеек I10 и J9, получаем =I9+МАКС(I22;J21), оба аргумента функции МАКС находятся в рабочей таблице.

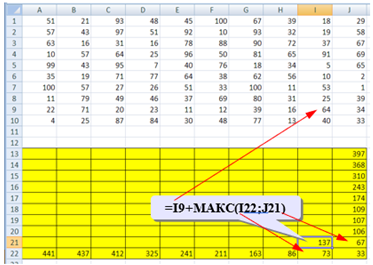
Рис. 3. Поиск оптимального пути внутри диапазона

Для всех оставшихся ячеек принцип вычисления максимальной суммы тот же самый: нужно добавить к значению этой ячейки в исходной таблице максимум из накопленных сумм, которые Робот собирает в случае двух возможных шагов; копируем формулу из I21 на весь диапазон A13:I21.

Первый ответ к задаче – это максимальная сумма, накопленная при движении из левого верхнего угла, она записана в левом верхнем углу рабочей таблицы, то есть в ячейке A13. Чтобы найти наименьшую возможную сумму, нужно в формуле заменить функцию МАКС на МИН: =I9+МИН(I22;J21).

Ответ: 1204 502

Таким образом, Excel является одним из самых универсальных продуктов Microsoft Office. Умение работать в нем пригодится почти для любой профессии. Excel подходит администраторам баз данных, бухгалтерам, экономистам и финансовым работникам, банковским служащим, менеджерам по продажам, маркетологам, логистам, руководителям. Программа позволяет создавать и быстро заполнять базы данных; проводить сложные расчеты с применением встроенных функций; проводить анализ данных любой сложности.

Поэтому умение обрабатывать данные в электронных таблицах и введение этой темы в программу ЕГЭ продиктовано необходимостью формирования компетенций, необходимых выпускнику школы.

Список литературы:

1.                 Волков, В. Б. Понятный самоучитель Excel 2010 / В.Б. Волков. — Санкт- Петербург : Питер, 2010. — 256 с.: ил.

2.                 Деордица, Ю.С. Учебно-методическое пособие / Ю.С. Деордица. — Луганск: ВНУ им. В. Даля, 2014. — 34 с.

3.                 ЕГЭ. Информатика и ИКТ: подбор заданий. – Текст : электронный  // ФЕДЕРАЛЬНЫЙ ИНСТИТУТ ПЕДАГОГИЧЕСКИХ ИЗМЕРЕНИЙ. Открытый банк тестовых заданий : [сайт]. – 2021. – URL: http://os.fipi.ru/tasks/5/a   (дата обращения: 24.03.2021).

4.                 Кодификатор элементов содержания и требований к уровню подготовки выпускников образовательных организаций для проведения единого государственного экзамена по информатике и ИКТ. – Текст : электронный // Федеральная служба по надзору в сфере образования и науки  ФГБНУ «ФЕДЕРАЛЬНЫЙ ИНСТИТУТ ПЕДАГОГИЧЕСКИХ ИЗМЕРЕНИЙ» : [сайт]. – 2021. – URL: file:///C:/Users/6145~1/AppData/Local/Temp/Rar$DIa0.692/ИНФ-11%20ЕГЭ%202021%20КОДИФ.pdf  (дата обращения: 24.03.2021).

5.                 Спецификация контрольных измерительных материалов для проведения в 2021 году единого государственного экзамена по информатике и ИКТ. – Текст : электронный // Федеральная служба по надзору в сфере образования и науки  ФГБНУ «ФЕДЕРАЛЬНЫЙ ИНСТИТУТ ПЕДАГОГИЧЕСКИХ ИЗМЕРЕНИЙ» : [сайт]. – 2021. – URL: file:///C:/Users/6145~1/AppData/Local/Temp/Rar$DIa0.090/ИНФ-11%20ЕГЭ%202021%20СПЕЦ.pdf (дата обращения: 24.03.2021).

6.                 Скачано с www.znanio.ru