ИСПОЛЬЗОВАНИЕ СВОЙСТВ ЧИСЛОВЫХ

Использование свойств числовых
неравенств при оценке значения выражения

Цели: закрепить знание теорем, выражающих основные свойства числовых неравенств; формировать умение применять изученные свойства при оценке значения выражения.

Ход урока

I. Организационный момент.

II. Устная работа.

1. Сформулируйте теоремы, выражающие основные свойства числовых неравенств. Для каждой теоремы приведите примеры.

2. На основании какого свойства можно утверждать, что если x < y, то:

а) x + 20 < y + 20;                      б) x – 20 < y;             в) y > x;

г) x  < y;                               д) –3x > –3y;             е) .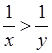

3. Каков знак числа а, если:

а) 7a > 2a;                                   б) –5a < –3a;             в) 5a < 4a.

III. Проверочная работа.

В а р и а н т  1

1. Зная, что b > a, c < a и d > b, сравните числа a и d; b и c.

2. Сравните с нулём числа a и b, если известно, что:

а) a + 5 > b + 5 и b > 0,5;                      б) –12a > –12b и b < –1.

В а р и а н т  2

1. Известно, что d > b, c < a и b > a. Расположите числа a, b, c, d в порядке возрастания.

2. Сравните с нулём числа a и b, если известно, что:

а) a + 1,2 > b + 1,2 и b > 3;                  б) –4a < –4b и b > 1.

IV. Формирование умений и навыков.

1. № 754 устно.

2. № 755.

Р е ш е н и е

a, b, c, d – положительные числа, значит, если:

1) a > b, то ;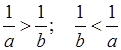

2) d < b, то ;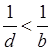

3) c > a, то .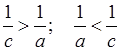

Имеем: .

О т в е т: .

3. Известно,  что  a > b.  Расположите  в  порядке  возрастания  числа:
a + 2; b – 8; a + 11; b; b – 6; a.

Р е ш е н и е

a + 2 > a, так как a + 2 – а = 2 > 0;

a + 11 > a + 2, так как a + 11 – (a + 2) = a + 11 – а – 2 = 9 > 0;

b – 6 < b, так как b – 6 – b = –6 < 0;

b – 8 < b – 6, так как b – 8 – (b – 6) = b – 8 – b + 6 = –2 < 0.

Имеем: a + 11 > a + 2; a + 2 > a; a > b; b > b – 6; b – 6 > b – 8.

О т в е т: b – 8; b – 6; b; а; a + 2; a + 11.

4. Перед выполнением следующих заданий следует напомнить учащимся, что неравенства одного знака a < b и b < c можно записать в виде двойного неравенства a < b < c.

Следует проанализировать, как можно преобразовать двойное числовое неравенство, используя свойства числовых неравенств. Особое внимание уделить видоизменению неравенства при умножении на отрицательное число («переворачиваем» неравенство).

Метод оценивания значения числового выражения следует разобрать на примере со с. 158 учебника.

№ 757.

Р е ш е н и е

3 < a < 4.

а) 3 ∙  5 < a ∙  5 < 4 ∙  5; 15 < 5a < 20.

б) 3 ∙  (–1) < a ∙  (–1) < 4 ∙  (–1); –4 < –a < –3.

в) 3 + 2 < a + 2 < 4 + 2; 5 < a + 2 < 6.

г) 5 – а = –1 · а + 5, значит, –4 + 5 < –а + 5 < –3 + 5; 1 < 5 – a < 2.

д) 3 ∙  0,2 < 0,2а < 4 ∙  0,2; 0,6 + 3 < 0,2а + 3 < 0,8 + 3; 3,6 < 0,2 + 3 < 3,8.

№ 759.

Р е ш е н и е

1,4 << 1,5.

а) 1,4 + 1 <+ 1 < 1,5 + 1; 2,4 <+ 1 < 2,5.

б) 1,4 – 1 <– 1 < 1,5 – 1; 0,4 <– 1 < 0,5.

в) 2 –= (–1) · + 2; 1,4 · (–1) > (–1) · > 1,5 · (–1);

–1,5 < –< –1,4; –1,5 + 2 < –+ 2 < –1,4 + 2; 0,5 < 2 –< 0,6.

№ 762.

При выполнении этого упражнения используем следствие теоремы 4. Обращаем особое внимание учащихся, что утверждение справедливо только для положительных чисел.

Р е ш е н и е

а) 5 < y < 8, значит, , то есть .

б) 0,125 < y < 0,25,  < y < , значит, 8 >  > 4, то есть 4 <  < 8.

5. № 761.

В этом упражнении демонстрируется практическое применение свойств числовых неравенств.

Р е ш е н и е

а) Пусть а см – сторона квадрата, тогда Р = 4а см – периметр квадрата.

5,1 ≤ а ≤ 5,2;   5,1 · 4 ≤ 4а ≤ 5,2 · 4;   20,4 ≤ 4а ≤ 20,8.

б) Пусть  Р  см  –  периметр  квадрата,  тогда  а =  см  –  сторона  квадрата.

15,6 ≤ Р ≤ 15,8;   15,6 : 4 ≤  ≤ 15,8 : 4;   3,85 ≤ а ≤ 3,95.

О т в е т: а) 20,4 ≤ 4а ≤ 20,8; б) 3,85 ≤ а ≤ 3,95.

6. Данное упражнение более сложное по сравнению с предыдущим и носит развивающий характер.

Пусть а и b – отрицательные числа. Верно ли, что:

а) если a < b, то а² < b²;

б) если а² < b², то а < b?

Р е ш е н и е

а) Если a < b,  то а – b < 0 (I).  Так  как  а и b – отрицательные  числа, то (а + b) – отрицательное число, то есть а + b < 0. Домножим обе части неравенства I на (а + b), поменяв знак неравенства:

(а – b)(а + b) > 0 · (а + b);

(а – b)(а + b) > 0;

а² – b² > 0, значит, а² > b², то есть утверждение неверное.

б) а² < b², значит, а² – b² < 0; (а – b)(а + b) < 0. Разделим обе части неравенства на отрицательное число (а + b). Получаем а – b > 0; а > b,то есть утверждение – неверное.

О т в е т: а) нет; б) нет.

V. Итоги урока.

В о п р о с ы   у ч а щ и м с я:

– Сформулируйте основные свойства числовых неравенств.

– В каком случае целесообразно записать неравенства в виде одного двойного неравенства?

– Каким образом используют основные свойства числовых неравенств при оценке значения выражения?

Домашнее задание.

1. № 758, № 760.

2. Известно, что а > b > 0. Поставьте вместо * знак > или < так, чтобы получилось верное неравенство:

а) 8а * 6b;                                               в) –6а * –4b;

б) 12а * b;                                               г) –11а * –3b.

3. Известно,  что  а < b.  Расположите  в  порядке  возрастания  числа:
а – 2; b + 3; а – 17; а; b + 23; b.

Д о п о л н и т е л ь н о е   з а д а н и е  № 756*.