МУНИЦИПАЛЬНОЕ КАЗЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

  СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 8 Г. КИЗИЛЮРТ

 

 

Исследовательская работа

на тему

«Пушкин и математика»

 

 

Работа выполнена: ученицей 8 В класса

Патхулаевой Айшат

под руководством:

учителя математики   Малик Е. В.

учителя русского языка    Далгатовой А.Ш.

     МКОУ СОШ № 8 г. Кизилюрт

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2018 г.

 

 

 

Содержание работы

 

 

 

 

 

 

1.     Введение.

            Обоснование актуальности учебного исследования

 

2.     Основная часть.

Содержание исследования. Предметы исследования. .

 

3.     Заключение.

Теоретическая и практическая значимость исследования.

 

    4.  Литература.                                                                                                                                                     

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I.      Введение

II.   

Актуальность исследования

 

            Широко распространено мнение, что А. С. Пушкин был не совсем в ладах с математикой. Из воспоминаний старшей сестры Ольги мы узнаем, что в детстве, бывало, он плакал над задачами по арифметике. По результатам вступительных экзаменов в лицей, об  Александре Пушкине записано, что «в познании языков: российского - очень хорошо, немецкого – не учился, в арифметике – знает до тройного правила, в познании общих свойств тел – хорошо, в начальных основаниях географии и начальных основаниях истории – имеет сведения». В воспоминаниях об учёбе в лицее «первый друг» и «друг бесценный» Иван Пущин рассказывал о том, как однажды их учитель по физике и математике Яков Иванович  Карцов  вызвал Пушкина к доске решать алгебраическую задачу. Переминаясь с ноги на ногу, Пушкин молча сделал на доске какие-то записи чисел. На вопрос учителя: «Ну, что же у Вас получилось? Чему ровняется икс?» - ученик улыбнулся и ответил: «Нулю!». «Хорошо, - подытожил Карцов. – У вас, Пушкин, всё в моём классе кончается нулём. Садитесь на место и пишите стихи». С. Д. Комовский вспоминал: «…Вообще он жил более в мире фантазии. Набрасывая же свои мысли на бумагу, везде, где мог, а чаще всего во время математических уроков, от нетерпения он грыз обыкновенно перо и, насупя брови, надувши губы, с огненным взором читал про себя написанное». В «Дневнике» поэта за 1 января 1834 года  находим запись: « Меня спрашивали, доволен ли я моим  камер – юнкерством. Доволен, потому что государь имел намерение отличить меня, а не сделать смешным, а по мне хоть в камер – пажи, только бы не заставили учиться французским вокабулам и арифметике».

            К 150-летию со дня рождения поэта Институт русской литературы (Пушкинский дом) издал «Словарь языка Пушкина» в четырёх томах по 800 страниц. «Словарь…» содержит 16 000 слов в алфавитном порядке с указанием числа раз встречающихся слов и ссылками на полное собрание сочинений. Например: алгебра встречается три раза, геометрия – три, физика – один, астролог – один, наука – 75, любить – 614, любовь – 630. Но на страницах гениальных творений Пушкина нашли отражение математические понятия, термины и идеи. Значит, связи поэта с современной ему математикой весьма многообразны?

 

      Проблема моего исследования, таким образом, состоит в осмыслении противоречий между:

-внешней нелюбовью к математике великого русского поэта и отражениями математических понятий, терминов и идей в рукописях и черновиках;

- точной наукой математикой и законами стихосложения.

Тогда объектом исследования является изучение работ и произведений А. С. Пушкина, в которых упоминаются или используются математические идеи.

Предмет исследования – это математическая лексика, законы математики, математические понятия в произведениях А. С. Пушкина.

Проблема, объект и предмет исследования определили тему исследования  «Пушкин и математика».

Цель - выяснить, насколько прослеживалась связь творчества с точной наукой математикой в литературном процессе А. С. Пушкина.

 

Задачи исследования:

 

1) изучить воспоминания близких, родственников, современников А. С. Пушкина;

2) изучить художественные тексты поэта;

3) проанализировать лексику поэта, законы, математические явления в исследуемых текстах А.С. Пушкина.

 

Методы исследования:

 

Ø  эмпирические: изучение научной, художественной, публицистической, литературы, материалов на электронных  носителях по проблеме исследования; наблюдение, опытно – экспериментальная работа;

Ø  теоретические: анализ, синтез, обобщение.

 

II. Основная часть. Содержание исследования.

Предметы исследования:

 

1.Гипотеза о форме цифр

 

            В материалах записных книжек Пушкина за 1835 год содержится гипотеза о происхождении формы цифр: «Форма цифр арабских составлена из следующей фигуры: АД(1), АВДС(2), АВЕСД(3), АВД + АЕ (4). Русские цифры составлены по тому же образцу». Следует, однако, признать, что эта гипотеза поэта для объяснения формы наших цифр не имеет никакого исторического обоснования. Русский ориенталист Георг Яковлевич Кер (1692 -1740) впервые в науке высказал мысль об индийском происхождении так называемых «арабских» цифр, что было признано лишь в 19 веке. Даже до сих пор в некоторых учебниках по математике цифры ошибочно называются арабскими. Индийские цифры попали в Европу от арабов в 12 веке через Мавританию. Пушкин, сравнивая татарское иго с игом мавританским в Испании, отметил: «Татары не походили на мавров. Они, завоевав Россию, не подарили ей ни алгебры, ни Аристотеля». Эволюция форм начертания индийских цифр имеет длинную историю, а современный вид они приняли лишь в эпоху Возрождения в трактате А. Дюрера (1471-1528) «Наставление к измерению циркулем  и линейкой» (1525).

 

 

2. «Серебряное сечение»

 

Многим хорошо известна эстетика золотого сечения. Недавно петербургский поэт и переводчик А. Чернов, «проверив алгеброй гармонию» поэмы «Медный всадник» (1833) Пушкина, обнаружил в нём своеобразное «серебряное деление». Математическую закономерность принципа «серебряного сечения» Чернов впервые обнаружил в тексте загадочного древнерусского памятника «Слово о полку Игореве» в виде отношения:

Число стихов в всех трёх частях «Слова…» (их 80)    

Число стихов  в первой и последней части (256)

Приблизительно ровно  3, 14, что является общеизвестным приближённым значением числа П (отношение длины окружности к её диаметру).

В «Медном Всаднике» А. С. Пушкин также использовал круговую композицию. Поделив число строк в издании поэмы под редакцией Б. В. Томашевского на её «диаметр», Чернов получил число, близкое к П.

 

3. «И случай, бог изобретатель».

 

В творчестве Пушкина в различных вариациях встречаются слова: тайна, надежда, судьба, судьбина, рок, тайный рок, пророк, провиденье, случайно, случай, фортуна, блуждающая судьба, святое провиденье, тайны роковые и т. п. Все эти слова загадочным образом связаны с наукой о случайном. Много надежд Пушкин возлагал на издание журнала «Современник». При жизни поэта  вышло четыре номера. В частности, в третьем томе «Современника» была помещена статья профессионального дипломата, поэта и популяризатора точных наук князя  Петра Борисовича Козловского (1783 – 1840) «О надежде». Это было первое в отечественной литературе популярное изложение основ теории вероятностей, названной автором «теорией удобосбытностей».

В рецензии на работу «История русского народа» редактора «Московский телеграф» Н. А. Полёва Пушкин мудро указывал: «…Но провидение не алгебра. Ум человеческий, по простонародному выражению, не пророк, а угадчик, он видит общий ход вещей и может выводить из оного глубокие предположения, часто оправданные временем, но невозможно ему предвидеть случая – мощного мгновенного орудия провидения…». Тайна случайности неоднократно и загадочно звучит в его стихах:

                                                 Дар напрасный, дар случайный,

         Жизнь, зачем ты мне дана?

       Иль зачем судьбою тайной

Ты на казнь осуждена?

Невероятно, но поэтическое отражение некоторых свойств случайных событий можно усмотреть и в  стихотворении «Зимний вечер» (1825):

Наша ветхая лачужка

И печальна и темна.

Что же ты, моя старушка,

Приумолкла у окна?

Или бури завываньем

  Ты, мой друг, утомлена,

            Или дремлешь под жужжанье

                                              Своего веретена?

Здесь случайное событие:

Что же ты, моя старушка,

Приумолкла у окна?

Складывается из двух несовместимых случайных событий:

Или бури завываньем

Ты, мой друг, утомлена,

Или дремлешь под жужжанье

Своего веретена?

В незаконченном стихотворении о научном творчестве (1829) Пушкин даёт глубокие определения случаю, опыту и гению:

О, сколько нам открытий чудных

Готовят просвещенья дух

И опыт, сын ошибок трудных,

И гений, парадоксов друг,

И случай, бог изобретатель.

Глубину этих определений специально отмечал ещё академик С. И. Вавилов.

В настоящее время на основе произведений Пушкина авторы современных задачников по теории вероятности с удовольствием включают задачи на классическое определение вероятности. Например:

  1. Какова вероятность сочинить первую  строку из романа А.С.Пушкина «Евгений Онегин»?

  2. Из колоды карт (52 листа) Герман наугад извлекает три карты. Найдите вероятность того, что это будут 3,7 и туз.

  В 4 главе «Евгения Онегина» в ночь перед дуэлью в романтических стихах Ленского Пушкин описывает закон распределения случайной величины Х («судьбы закон»):

Куда, куда вы удалились,

Весны моей златые дни?

Что день грядущий мне готовит?

Его мой взор напрасно ловит,

В глубокой мгле таится он.

Нет нужды; прав судьбы закон.

Паду ли я, стрелой пронзённый,

Иль мимо пролетит она,

Всё благо: бдения и сна

Приходит час определённый;

Благословен и день забот,

Благословен и тьмы приход!

 

            Здесь случайная величина Х – судьба, которая принимает значения «день забот» и «тьмы приход» с равными вероятностями, что передаётся словами «благословен».

Отблеск идеи расчёта зависимости между случайными величинами по методу наименьших квадратов находит яркое отражение в известном стихотворении поэта «Портрет» (1828), посвящённом красавице А. Ф. Закревской:

С своей пылающей душой,

С своими бурными страстями,

О жёны Севера, меж вами

Она является порой

И мимо всех условий света

Стремится до утраты сил,

Как беззаконная комета

В кругу, расчисленном светил

 

Однако движение кометы столь же «расчислено» (закономерно), как и движение небесных светил. Как тут не подумать: «О, наука о случайном, как беспощаден твой расчёт!»

В 7 главе романа «Евгений Онегин» Пушкин проиронизировал над авторами «расчислений» «философических таблиц» по поводу прогнозов русских последователей французского математика, экономиста и политического деятеля Ш. Дюпина  (1784 - 1873)

Когда благому просвещенью

Отдвинем более границ,

Со временем (по расчисленью

Философических таблиц,

Лет через пятьсот) дороги, верно,

У нас изменятся безмерно…

 

4.«Евгений Онегин» и Марковские цепи.

 

Как известно, академик А. А. Маркин (1856 -1918) провёл статистические исследования чередования гласных и согласных в романе Пушкина «Евгений Онегин». Об этом он впервые сообщает русскому учёному – математику А. А. Чупову (1874 -1926) в письме от 15 января 1913 г. «Второй вопрос относится к произведённому мною своеобразному статистическому исследованию, которым я предполагаю закончить свою книгу. Характер исследования, которое обнимает последовательность 20 000 букв в романе Пушкина «Евгений Онегин», не считая «ъ» и «ь»; эта последовательность обнимает всю первую главу и шестнадцать строф второй.

«Мой дядя самых честных правил, 16с.,9г.

Когда не в шутку занемог, 12с.,8г.

Он уважать себя заставил 11с., 9г.

И лучше выдумать не мог. 10с., 8г.

Его пример другим  наука; 11с.,9г.

Но, боже мой, какая скука 10 с.,8г.

С больным сидеть и день, и ночь 12с., 9г.

Не отходя ни шагу прочь! 9с., 8г.

Какое низкое коварство 11с., 9г.

Полуживого забавлять, 9с., 8г.

Ему подушки поправлять, 11с., 9г.

Печально подносить лекарство, 15с., 8г.

Вздыхать и думать про себя:12с., 9г.

Когда же чёрт возьмёт тебя!» 13с., 8г.

 

 Соответственно этому мы допускаем существование неизвестной постоянной вероятности р букве быть гласной и приближённую величину р ищем из наблюдений, считая число появившихся гласных и согласных букв. Кроме числа р мы найдем, также из наблюдений, приближённые величины двух других чисел р₁  и р_{2 ,}  представляющих вероятности первое р₁  - гласной букве следовать за гласной, второе р₂  - гласной букве следовать за гласной». У Маркова указанные величины равны:

    р = 0, 432, р₁  = 0,128, р₂=0, 663 и б = р₁  – p₂  = - 0, 535.

Эти и другие исследования Маркова подтвердили достаточно хорошее совпадение реального следования гласных и согласных с гипотезой о наличии простой цепной зависимости. Марковские цепи послужили началом создания теории марковских процессов, играющих большую роль в науке.

 

5. О вдохновении.

 

В критической статье, посвящённой работе В. К. Кюхельбекера, Пушкин в 1826 году писал: «Вдохновенье нужно в поэзии, как в геометрии».  Примерно в это же  время, но уже по другому поводу, поэт в своей тетради запишет: «Вдохновение нужно в геометрии, как и в поэзии», поменяв местами слова о геометрии и поэзии. Этим он подчеркнул равноправие поэзии и геометрии перед вдохновением. Но только ли это? Пушкиновед академик М. П. Алексеев  отмечал,  что  эта  перестановка  слов  не  случайна.  К этому времени

Н. И. Лобачевский  уже  произнёс свою историческую речь о воображаемой  геометрии  24 февраля  1824 года в Казанском университете, и отзвуки речи учёного вполне могли достигнуть Пушкина. Больше того, с довольно большой вероятностью можно предположить о личной встрече двух гениев. Из биографии Пушкина известно, что в сентябре 1833 года он проездом был в Казани, где собирал материал об «Истории пугаческого бунта». К этому времени Лобачевский уже много лет был ректором Казанского университета. Их встреча могла произойти в стенах университета или его библиотеке. Из биографии Лобачевского известно, что он любил поэзию Пушкина и часто читал его стихи наизусть в кругу семьи. Кроме этого, брат жены учёного офицер И. Е. Великопольский был давнишним приятелем поэта и даже обменивался с ним стихами. Эти факты благоприятствуют возможной встрече гостившего в хлебосольном доме учёного. Наконец, встреча могла произойти в доме профессора Казанского университета Фукса, где устраивалась вечера, и бывало много гостей. Пушкин несколько дней гостил в доме  Фукса и поэтому, кажется невероятным, чтобы в один из «пушкинских вечеров» не был бы там, в гостях, и Лобачевский. А пока, к сожалению, приходится признать, что до сих пор не удалось найти документальных свидетельств  встречи двух гениев.

                                                                                                                                                                                                                                                                                                                                     

                                                     

6. Из рассказа летописца.

 

             Известно, что Пушкин имел намерение написать биографию Николая Григорьевича Курганова (1725 – 1796) – талантливого самородка, сына унтер – офицера, ставшего в 39 лет профессором математики и навигации. Его «Универсальная арифметика» (1757) заменила знаменитую «Арифметику» (1703) Л. Ф. Магницкого  в школах и различных специальных учебных заведениях России. Для сбора материалов к биографии Н. Г. Курганова Пушкин предпринял специальные поиски, расспрашивал старых литераторов, копался в старинных журналах, но так и не смог узнать даже, когда он жил и где служил. Больше всего Пушкина Курганов интересовал как автор знаменитого «Письмовника» (такое название получила «Российская универсальная грамматика» (1769)). «Письмовник» Курганова был своеобразной энциклопедий и самой популярной книгой в России 18 века и выдержал свыше десяти изданий. В повести «История села Горюхина» (1830) Пушкин вложил в уста горюхинского летописца рассказ: «Чтение письмовника долго было любимым моим упражнением. Я знал его наизусть и, несмотря на то, каждый день находил в нём новые незамеченные красоты. После генерала Племянникова, у которого батюшка был некогда адъютантом, Курганов казался мне величайшим человеком. Я расспрашивал о нём у всех и, к сожалению, никто не знал его лично, на все мои вопросы отвечали только, что Курганов сочинил Новейший письмовник, что твёрдо знал я и прежде. Мрак неизвестности окружал его как некоего древнего полубога; иногда я даже сомневался в истине его существования. Имя его казалось мне вымышленным и предание о нём пустою мифою, ожидавшею изыскания нового Бартольда Георга Нибура (1776-1831)- немецкий историк древнего мира. Однако же он всё преследовал моё воображение, я старался придать какой – нибудь образ сему таинственному лицу…».

 

 

7. Знал ли Пушкин числа Фибоначчи?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Числа Фибоначчи — элементы числовой возвратной последовательности 1, 1, 2, 3, 5, 8, ... (ряда Фибоначчи), в которой каждый последующий член равен сумме двух предыдущих, таким образом, последовательность u1, u2,…чисел Фибоначчи  задается начальными соотношениями u1 = u2 = 1 и рекуррентным соотношением un+1 =  un-1 + un.

 

 

Многое в структуре произведений поэзии род­нит этот вид искусства с му­зыкой. Четкий ритм, зако­номерное чередование ударных и безударных сло­гов, упорядоченная раз­мерность стихотворений, их эмоциональная насы­щенность делают поэзию

родной сестрой музыкальных произведений. Каждый стих обла­дает своей музыкальной формой - своей ритмикой и мелодией. Можно ожидать, что в строении стихотворений проявятся неко­торые черты музыкальных композиций, закономерности музы­кальной гармонии, а, следовательно, и золотая пропорция, и чис­ла Фибоначчи.

Исследования поэтических произведений с этих позиций только начинаются. И начинать нужно с поэзии А.С. Пушкина. Ведь его произведения - образец наиболее выдающихся творений русской культуры, образец высочайшего уровня гармонии. С поэзии А.С. Пушкина мы и начнем поиски золотой пропорции - мерила гармонии и красоты.

Для анализа метрики стихотворений А.С. Пушкина рассмот­рены его произведения периода 1829-1836 годов, периода созда­ния наиболее совершенных стихов. Сюда вошло 109 стихов (без песен западных славян). Число строк в стихотворениях этого пе­риода изменялось от 4 до 116. Однако большие стихотворные фор­мы встречаются редко; число стихотворений с числом строк бо­лее 60 составило всего девять штук. Средний размер этих стихот­ворений составил 88 строк.

Казалось бы, величина стихотворения, определяемая чис­лом строк, может изменяться произвольно и непрерывно от самой малой в четыре строки до самых больших, насчитываю­щих десятки строк. Однако оказалось, что это не так. Размеры стихов распределены совсем не равномерно; выделяются пред­почтительные и редко встречающиеся размеры. На графике распределения стихотворений А.С. Пушкина по числу строк в них отчетливо выделяется несколько максимумов - наиболее часто встречающихся размеров (см. рисунок). Они явно тяго­теют к числам 5, 8, 13, 21, 34. Причем по мере увеличения размеров стихотворений эти максимумы как бы «размывают­ся», нивелируются. Максимум в области 46-55 строк выражен совсем слабо.

 

 

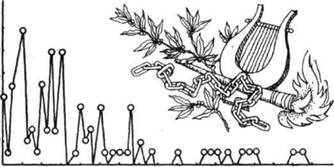
Ч   8   12 16 20 24 28 32 36 40 W 48 52 56 60 64 68

 

Проявляется вполне зако­номерная тенденция в твор­ческой манере поэта; он явно предпочитает стихотворения, размер которых близок к чис­лам ряда Фибоначчи. Следу­ет учесть, что законы стихос­ложения требуют, как прави­ло, наличия четного числа строк в стихотворении, так как строки попарно рифмуются. Неудивительно поэтому, что сти­хотворения с числом 12 и 14 встречаются значительно чаше, чем с числом строк 13. Это же справедливо и для интервала 20-22 строки. С учетом этого правомерно сгруппировать стихотворения по их размерам к некоторым областям, расположенным около чисел Фибоначчи. В результате стихотворения распределились следую­щим образом:

5 ± 1 строка - 14,

8 строк - 12, 14 ± 2 строки - 32,

22 ±2-15, 32 ±2-8 штук.

Общее число этих стихотворений составило 81, или около 80% к их общему числу.

... Характерно также, что наиболее выдающиеся произведения поэта, шедевры его творчества явно тяготеют к размерам 8, 13, 21 и 34 строки. К ним относятся стихи «В крови горит огонь жела­ний...», «Я вас любил, любовь еще, быть может...», и, наконец, одно из последних: «Пора, мой друг, пора! покоя сердце просит...», - все они состоят из восьми строк. В таких замечательных произве­дениях поэта, как «Сонет», «Поэту», «Мадонна», «Няне», - 13-14 строк. По 20 строк в таких известных стихотворениях, как «Храни меня, мой талисман», «Во глубине сибирских руд», «Поэт», «Когда в объятия мои», «Я здесь, Инезилья...» и в предсмертном «Я памятник себе воздвиг нерукотворный...»

Числа Фибоначчи не только доминируют в размерах стихот­ворений А.С. Пушкина, они определяют во многих случаях и внут­реннюю композицию стихотворений: число стихов и число строк в них. Из 106 рассмотренных стихотворений его в 54 встречаются числа 3, 5, 8, 13, 21, 34, 55. В 16 произведениях стихи состояли из восьми строк (3 х 8, 5 х 8, 8 х 8). Так, в стихотворении «Моя родословная» - 8 восьмистиший, в стихотворении «Друзьям» и «Дорожные жалобы» - 8 четверостиший. Конечно, число 8 удобно для стихосложения еще и потому, что оно четное. Но ведь четными являются и числа 6 и 10, однако они встречаются в произведениях поэта крайне редко.

... Преобладание в метрике стихотворений А.С. Пушкина чисел ряда Фибоначчи никак нельзя признать случайностью, игрой слепой вероятности. Наличие этих чисел выражает одну из фундаменталь­ных закономерностей творческого метода поэта, его эстетические требования, чувство гармонии. Характерно, что нечетные числа это­го ряда 3, 13, 15, 21 затрудняют стихосложение, рифмование строк. Но поэт пользуется этими размерностями, так как они отвечают тре­бованиям художественной формы, формы новой, необычной, ориги­нальной и в то же время отвечающей критериям гармонии.

В коротких стихотворениях размером в 4-8 строк, как прави­ло, выражена одна мысль, эмоциональное состояние поэта. Но сти­хотворения более значительные по размеру, содержащие 12-14 или 20-22 строки, очень часто включают в себя две мысли, два эмоциональных нюанса. Поэтому такие стихотворения состоят как бы из двух частей. Такое деление стихов на две части бывает сим­метричным - произведение делится на две равные части. Но зна­чительно чаше части стихотворения не равны по размеру, асим­метричны. В таких произведениях отношение большей части к меньшей очень часто отвечает рядом расположенным числам Фи­боначчи (или близко к ним, учитывая четность числа строк) и, сле­довательно, близко к золотой пропорции. Некоторые стихотворе­ния А.С. Пушкина очень четко отвечают этой закономерности внутренней композиции.

В стихотворении «Поедем, я готов; куда бы вы, друзья...» со­держится 13 строк. В нем выделяются две смысловые части: пер­вая в 8 строк и вторая в 5 строк.

В стихотворении «Элегия» («Безумных лет угасшее веселье...») две части - 6 строк и 8 строк. В стихе «Нет, я не дорожу мятежным наслажденьем...» также выделяются две части размером в 6 и 8 строк.

... После приведенного анализа стихотворений А.С. Пушкина уже не, кажется простой случайностью тот факт, что его роман в стихах «Евгений Онегин» состоит из 8 глав, в каждой главе в сред­нем около 50 стихов (а глава 7-я состоит из 55 стихов), а каждый стих состоит из 14 строчек. Похоже, что основная схема построе­ния «Евгения Онегина» основана на близости к трем числам Фи­боначчи: 8, 13, 55. Тяготение Пушкина к этим числам очевидно и, конечно, не случайно.

... Тяготение к определенным стихотворным формам харак­терно для каждого поэта, оно и определяет его индивидуальность. Для А.С. Пушкина характерно большое разнообразие таких форм, но есть у него и наиболее излюбленные. По-видимому, сюда отно­сится и неосознанное, интуитивное тяготение к числам 5, 8, 13, 21, 34, 55. Ведь интуиция в творчестве А.С. Пушкина была необы­чайно сильной и плодотворной, во многом она и определила гени­альность его произведений.

... В метрике и композиции стихов А.С. Пушкина сосуществу­ют два начала, обеспечивающие их гармонию: симметрия и асим­метрия. Симметрия стихотворений выражается в четном числе рифмованных строк, в наличии 4-, 6- и 8-стиший, в парном коли­честве стихов в произведениях. Некоторые стихотворения сим­метричны по смысловому содержанию, которое делит их на две равные части (например «Город пышный, город бедный...», «Счас­тлив тот, кто избран своенравно...», «И.И. Пущину» и др.). Про­стота симметричных построений придает стихам красоту упоря­доченности, легкость восприятия, строгость и монументальность.

Различные формы асимметрии проявляются в существовании непарного числа строк, наличии структур стихосложения 3 х 5, 5 х 3, 5 х 7 и т. п., несимметричном расположении кульминацион­ных моментов, границ раздела стихотворений на различные по содержанию или интонации части. Асимметрия придает стихам живость, повышает эмоциональное воздействие. Одним из выра­жений асимметрии в метрике и композиции стихов является золо­тая пропорция, подчинение метрики числам Фибоначчи. Как из­вестно, числа Фибоначчи отражают особенности роста живого, эти же особенности проявляются и в рождении, и в росте стихот­ворных творений поэта. Сочетание этих двух основ гармонии и порождает удивительное разнообразие художественных форм в поэзии А.С. Пушкина.

... Рассмотрим композицию «Пиковой дамы». В этой повести кульминационным моментом является сцена в спальне графини, куда проник Германн в надежде узнать тайну трех карт, сцена, которая оканчивается смертью графини. В повести (издания 1978 г.) 853 строки. Кульминационный момент повести - это смерть графини. Ему отвечает 535-я строка: «Потом покатилась навзничь... и осталась недвижима». Эта строка расположена в по­вести почти точно в месте золотого сечения, так как 835: 535 = 1,6. Читатель может возразить, что кульминационным моментом является восклицание Германна: «Старая ведьма! Так я ж застав­лю тебя отвечать» - или момент, когда Германн убедился, что она умерла. Не будем вдаваться в мелкие детали этой сцены, тем бо­лее что речь идет здесь о разнице всего в несколько строк.

Наличие золотой пропорции и определяет основной план ком­позиции «Пиковой дамы», придает ей гармоническую асиммет­ричность: медленное нарастание эмоционального напряжения повествования, кульминация - смерть графини и постепенный спад эмоционального накала во второй части повествования.

Повесть «Пиковая дама» состоит из шести глав. Посмотрим, не проявляется ли в композиции глав золотая пропорция? В пер­вой главе золотому сечению отвечает 68-я строка (всего в главе 110 строк): «Сен-Жермен задумался». Но ведь это уже узловая точка повествования, в ней переломный момент всей главы: от­кроет ли Сен-Жермен свою тайну графине, выручит ли ее, изба­вив от огромного карточного долга, или... графиня будет обрече­на на разорение и позор.

Вторая глава повести содержит 219 строк. Золотое сечение здесь приходится на 135-ю строку: «Однажды - это случилось два дня после вечера, описанного...» Но ведь это кульминационный момент главы, Лиза увидела в окне стоящего на улице Германна! Отсюда начался для нее новый отсчет времени, начались события, определившие всю ее дальнейшую судьбу. А.С. Пушкин совершен­но точно определил это место во второй главе в золотом сечении - будто по калькулятору рассчитывал число строк; ведь 219: 135 = 1,62.

Третья глава повести описывает усилия Германна попасть в дом старой графини, выведать у нее тайну трех карт. С помощью Лизы он проникает в дом графини, прячется в темном кабинете и ждет возвращения графини. «Он был спокоен; сердце его билось ровно, как у человека, решившегося на что-нибудь опасное, но необходимое. Часы пробили первый и второй час утра, - и он ус­лышал далекий стук кареты. Невольное волнение овладело им. Карета подъехала и остановилась».

Последняя фраза начинает новый отсчет времени для Герман­на (и для графини). Эта фраза приходится на 131-ю строку тре­тьей главы, а всего в ней 212 строк. Разделив

212: 131, мы полу­чим точно золотую пропорцию (212: 131 = 1,618)! Это порази­тельно! Какое фантастически точное интуитивное владение поэтом законами гармонической композиции!

В четвертой главе размером 113 строк золотая пропорция при­ходится на 70-ю строку: «Лизавета Ивановна выслушала его с ужа­сом». Это также переломный, трагический момент в жизни Лизы. Она вспомнила слова Томского: «У этого человека, по крайней мере, три злодейства на душе!» Она поняла с ужасом, что Германн ви­новник смерти графини, что Германна влекла не любовь к ней, а жажда денег.

В V главе описано посещение Германном похорон графини. Германн был «чрезвычайно расстроен» видом покойницы. В трак­тире он много выпил. «Возвратясь домой, он бросился, не разде­ваясь, на кровать и крепко заснул». Эта 46-я строка пятой главы разделила повествование на две части: первая - похороны графи­ни и приход к ней Германна и вторая - сон Германна, во время которого к нему явилась графиня и назвала три заветные карты - тройка, семерка, туз. Эта 46-я строка также отвечает золотой про­порции, ведь всего в этой главе 75 строк (75: 46 = 1,63).

В последней главе кульминационный момент заключен в возгла­се Германна: «Старуха!», который приходится на самый конец - на 5-ю строку от заключительной части повествования. Золотая пропор­ция приходится на 77-ю строку: «Германн выпил стакан лимонаду и отправился домой», которая завершает описание первого дня игры Германна в карты и первого его выигрыша. Как видим, и в компози­ции последней главы повести присутствует золотая пропорция.

... Совпадение кульминационных моментов в произведениях прозы у А.С. Пушкина с золотой пропорцией удивительно близ­кое, в пределах 1-3 строк. Чувство гармонии у него было развито необыкновенно, что объективно подтверждает гениальность ве­ликого поэта и писателя.

III. Заключение

 

Как видно, в лицейские годы чистая и прикладная математика юным Александром Пушкиным не воспринималось как «милые предметы». Зато впоследствии, когда он писал о своём стремлении «в просвещении стать с веком наравне», поэт, несомненно, проявил большой интерес к математике, что нашло отражение в его гениальных творениях. Друг поэта П. А. Вяземский (1792 – 1878) писал о Пушкине, что был «страстен и к наукам естественным и особенно математическим, которые составляли значительный капитал его познаний и были до конца любимым предметом его учёных занятий и глубоких исследований».

 

Теоретическая и практическая значимость исследования заключается в том, что этим материалом можно развеять миф о нелюбви поэта к точной науке математике, использовать в качестве доказательства близость таких явлений человеческой мысли и творчества как литература и математика.

 

Литература

 

 

1. А. С. Пушкин в воспоминаниях современников. – В 2-х т. – М.: 1981. – Т. 1.
2. Депман И. Я. История арифметики. – М.: Учпедгиз, 1959.
3. Краюхин С. Поверив алгеброй гармонию «Слова…», поэт обнаружил серебряное сечение. – Газета «Известия», № 19 /1996, 1 февраля.
4. Марков А. А. Пример статистического исследования над текстом «Евгений Онегина», иллюстрирующий связь испытаний в цепь. – Известия Академии наук. – Серия 8. – СПб. – Т. 8. - № 3, 1999г, с. 153 – 162.
5. Пушкин А. С. Полное собрание сочинений. – Т. 9. – М.: Академия, 1987.
6. Пушкин А. С. Сочинения. – В 3-х т. – М.: Художественная литература, 1985 – 1987.
7. Пушкин А. С. Собрание сочинений. – Т. 7. – М.: Наука, 1964, с. 144.
8. Тарзиманова Г. Стихотворение Лобачевского. – Журнал «Квант»,

     № 8/1980, с. 18 – 19.

9. Френкель В. Я. Пушкин и точные науки. – Журнал «Квант», № 8/1978, с. 28-32.
10. О теории вероятности и математической статистике (переписка А. А. Маркова и А. А. Чупрова). – М.: Наука, 1977.