Исследовательская работа Процентное содержание вещества. Метод Пирсона

Министерство науки и высшего образования Российской Федерации федеральное государственное бюджетное общеобразовательное учреждение высшего образования

«Российский экономический университет имени Г.В. Плеханова»

Улан-Баторский филиал

ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА

Международной научно-практической конференции юных исследователей

«Шаг в будущее»

на тему: «Концентрация вещества в растворах. Метод Пирсона»

Выполнил ученик 6г класса

Доноев Александр

Руководитель:

Русанова Л.В., учитель математики

Улан-Батор, 2024

 СОДЕРЖАНИЕ

I.Введение

II.Основная часть

II.I. Раздел теоретический

Глава 1. Основные понятия

Глава 2. Приготовление раствора

Глава 3.  Замена «Концентрации»

Глава 3. Метод Пирсона

II.II. Раздел практический

Глава 1. Задачи

Глава 2. Анкетирование

Глава 3. Мастер-класс

III. Заключение

IV. Список литературы

ВВЕДЕНИЕ

                                 «Три пути ведут к знанию -

                  Путь размышления -это путь самый благородный

   Путь подражания -это путь самый легкий

                          Путь опыта -это путь самый честный и трудолюбивый»

 Обучение решению задач на концентрацию вещества начинается с 6 класса и продолжается на продолжении всей основной школы. Меня заинтересовала данная тема и я запланировал понять и научиться решать такие задачи. В повседневной жизни мы часто сталкиваемся с ситуациями, когда требуется смешать различные жидкости, растворы, порошки, разбавлять что – либо водой. В математике уделяется большее внимание таким процессам. 

В последние годы в научной литературе нашло свое отражение описание метода «квадрат Пирсона» для смешивания двух растворов.

Актуальность работы: В современном мире существует ряд отраслей промышленности, в которых применяется смешивание растворов, смесей и сплавов. Это – пищевая, фармацевтическая, нефтегазовая, химическая отрасли. В быту люди постоянно сталкиваются с проблемами, как правильно приготовить маринад для консервирования, как смешать в правильных пропорциях клей для обоев, как разбавить уксусную кислоту для употребления в пищу. В последние годы в научной литературе нашло свое отражение описание метода «квадрат Пирсона» для смешивания двух растворов. Задачи данного типа все чаще встречаются в КИМах ОГЭ и ЕГЭ для подготовки и проведения экзамена по математике.

Цель работы:

Понять и научиться решать задачи на концентрацию вещества в растворах.

Для этого надо решить следующие задачи:

1) изучить материал из различных источников о концентрации вещества;

2) Рассмотреть решение простых задач (приготовить растворы);

3) проанализировать и систематизировать полученные данные, сделать выводы;

4)Провести анкетирование и мастер-класс.

5) оформить исследование в виде презентации;

6) выступить с презентацией на школьной научно-практической конференции;

7) заинтересовать других ребят своей работой.

Гипотеза: если я изучу «квадрат Пирсона» при решении задач на смешивание двух растворов, то научусь решать данные задачи.

Объект исследования: задачи на концентрацию веществ в растворах.

Предмет исследования: метод Пирсона.

Методы работы  исследования:

1)    Сбор и анализ информации по выбранной теме.

2)    Выбор наиболее интересных фактов о кубике.

3)    Проведение сборок.

4)    Создание презентации как продукта своей работы.

Этапы работы над работой :

1)подготовительный (поиск и сбор информации);

2) технологический (анализ и обобщение информации);

3) презентативный (создание презентации «);

4) заключительный (выводы о проделанной работе).

На защиту выносится презентация для тех, кому эта тема близка и интересна.

II. ОСНОВНАЯ ЧАСТЬ

II.I. Раздел теоретический.

Глава 1.  ОСНОВНЫЕ ПОНЯТИЯ

Раствором называется однородная система, состоящая из нескольких компонентов. Простейший раствор состоит из двух компонентов: растворителя и растворенного вещества. Растворителем считается жидкий компонент. Чаще всего растворителем бывает вода. Важнейшей характеристикой любого раствора является его концентрация.

Концентрация раствора показывает, в каком соотношении находятся растворенное вещество и растворитель. Это соотношение может быть показано разными способами.

концентрация=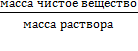

Следует помнить, что концентрация воды равна 0%, концентрация твёрдого безводного вещества- 100%.

Чтобы правильно понимать условия задач и тем самым прийти к верному решению, необходимо знать следующие понятия и определения:

Все получающиеся растворы однородны;

При решении таких задач считается, что масса растворов  нескольких веществ равна сумме масс компонентов;

Процент – одна сотая любого вещества;   

Для решения задач на смеси и сплавы существуют много различных методов. Чаще всего используют следующие методы решения задач на растворы:

Табличный;

Арифметический;

Алгебраический;

Определение выбора метода решения задач зависит от ее условия и от сложности задачи. Любую задачу можно решить несколькими способами, но не каждый способ будет рациональным и малозатратным.

Глава 2. Приготовление растворов

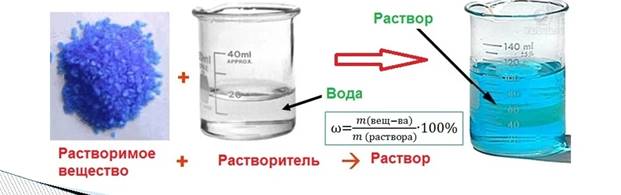
1.Взвесить безводное вещество на весах;

2.Отмерить мензуркой воду данного объёма в мл (в граммах что одно и то же);

3.Вещество высыпать в воду;

4. Перемешать до полного растворения;

5.Получится данный раствор.

Глава 3. Замена «концентрации»

Глава 4. Метод Пирсона.

Первооткрывателем данного метода является британский математик Карл Пирсон. Он родился 27 марта 1857 года в Лондоне. В возрасте 9 лет Пирсон был отправлен в школу университетского колледжа в Лондоне, где он учился до 16 лет. В 1875 году занял второе место на экзаменах в Кембридж и получил стипендию в Королевский колледж.

«Квадрат Пирсона» – это механический способ при решении задач на концентрацию, который позволяет рационально и экономно проводить вычисления. Этот способ имеет ещё два названия: химики называют этот способ «правило креста» или «конверт Пирсона». «Квадрат Пирсона» имеет предельно общий характер и применяется практически во всех естественных науках.

Так что же представляет из себя «квадрат Пирсона» и каков алгоритм решения задач с помощью этого способа? Изучение способа «квадрат Пирсона» позволило составить алгоритм решения задач на смеси и сплавы.

Алгоритм решения задач методом «квадрат Пирсона»:

1.начертить квадрат и провести в нем диагонали;

2.в верхнем левом углу квадрата с одной стороны записываем процентное содержание вещества в первом растворе х₁ %, с другой стороны массу этого вещества m_1;

3.в нижнем левом углу квадрата с одной стороны записываем процентное содержание вещества во втором растворе х₂ %, с другой стороны массу этого вещества m_2;

4.в точке пересечения диагоналей сверху записываем концентрацию полученной смеси х %, снизу общую массу смеси m (m₁₊ m₂);

5.находим разность  по первой диагонали и записываем её в правом верхнем углу_;

6.находим разность х_1-х% по второй диагонали и записываем её в нижнем правом углу ;

7.  Способ 1: решить пропорцию =

    Способ 2: полученные разности необходимо умножить на соответствующие массы исходных растворов и сумма этих выражений будет равна … + …= хm .

II.II. Раздел практический.

                                 Глава 2. Анкетирование в 6г классе

Глава 3. Мастер-класс

Я провёл мастер-класс в 6 г классе: дети научились готовить растворы процентного содержания вещества.

ЗАКЛЮЧЕНИЕ

Завершив свою работу, я могу сказать, что всё то, что было задумано, в целом получилось: умею готовить растворы заданной концентрации, владею методом Пирсона при смешивании двух растворов. Планирую изучить метод Пирсона при смешивании трёх растворов. В дальнейшем, я смогу использовать этот метод, при решении задач на растворы
в подготовке к ОГЭ и ЕГЭ.

Список литературы

1. Городнова О. А. Учимся решать задачи на смеси и сплавы, г-та «Математика» №36, 2004 г

2. Захарова, А.Е. Учимся решать задачи на смеси и сплавы. Математика для школьников. 2006.-С.18-21

3. Ковалева Т.И., Бузулина О.Л., Безрукова Ю.А. Математика: тренировочные тематические задания повышенной сложности с ответами для подготовки к ЕГЭ и к другим формам выпускного и вступительного экзаменов.– Волгоград: Учитель, 2009. – 494 с.

4. Мальцев Д.А., Мальцева Л.И., Каибханова С.З. и др. Математика 9 класс. Предпрофильная подготовка: учебно- методическое пособие. –Ростов н/Д: Издатель Мальцев Д.А, 2012. – 208 с.  

5. Прокопенко Н. И. Задачи на смеси и сплавы / Н.И. Прокопенко. - М.: Чистые пруды, 2010. – 215 с.

6. Райхмист Р.Б. Задачник по математике для учащихся средней школы и поступающих в вузы (с решениями и ответами): Учеб.пособие. – М.: Московский лицей, 2009. – 304 с.

Скачано с www.znanio.ru